بيت إنترنت

مصفوفة المعكوس المعطاة والخوارزمية لحسابها. ابحث عن المصفوفة العكسية على الإنترنت

الأولي وفقًا للصيغة: A^-1 = A*/detA، حيث A* هي المصفوفة المرتبطة، detA هي المصفوفة الأصلية. المصفوفة المرفقة هي مصفوفة الإضافات المنقولة إلى عناصر المصفوفة الأصلية.

أولًا، ابحث عن محدد المصفوفة، ويجب أن يكون مختلفًا عن الصفر، حيث سيتم استخدام المحدد كمقسوم عليه. لنفترض، على سبيل المثال، مصفوفة للثالث (تتكون من ثلاثة صفوف وثلاثة أعمدة). كما ترون، محدد المصفوفة لا يساوي الصفر، لذلك هناك مصفوفة معكوسة.

أوجد مكمل كل عنصر من عناصر المصفوفة A. المكمل لـ A هو محدد المصفوفة الفرعية التي تم الحصول عليها من الأصل عن طريق حذف الصف i والعمود j، ويتم أخذ هذا المحدد بعلامة. يتم تحديد الإشارة بضرب المحدد بـ (-1) أس i+j. وبالتالي، على سبيل المثال، سيكون مكمل A هو المحدد المذكور في الشكل. أصبحت العلامة هكذا: (-1)^(2+1) = -1.

ونتيجة لذلك سوف تحصل مصفوفةالإضافات، الآن قم بتبديلها. التحويل هو عملية متناظرة حول القطر الرئيسي للمصفوفة، حيث يتم تبديل الأعمدة والصفوف. وبذلك تكون قد وجدت المصفوفة المرتبطة A*.

هذا الموضوع هو واحد من أكثر المواضيع التي يكرهها الطلاب. والأسوأ من ذلك، على الأرجح، المحددات فقط.

الحيلة هي أن مفهوم العنصر العكسي (وأنا لا أتحدث فقط عن المصفوفات الآن) يحيلنا إلى عملية الضرب. حتى في المناهج الدراسية، يعتبر الضرب عملية معقدة، ويعتبر ضرب المصفوفات بشكل عام موضوعًا منفصلاً، ولدي فقرة كاملة ودرس فيديو مخصص له.

اليوم لن نخوض في تفاصيل حسابات المصفوفة. فقط تذكر: كيف يتم الإشارة إلى المصفوفات وكيف يتم ضربها وما يتبع ذلك.

مراجعة: ضرب المصفوفات

في البداية دعونا نتفق على التدوين. المصفوفة $A$ ذات الحجم $\left[ m\times n \right]$ هي ببساطة جدول أرقام يحتوي بالضبط على صفوف $m$ وأعمدة $n$:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( أ)_(21)) & ((أ)_(22)) & ... & ((أ)_(2ن)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrix) \right])_(n)\]

لكي لا تخلط بين الصفوف والأعمدة في الأماكن عن طريق الخطأ (صدقني، في الامتحان، يمكنك الخلط بين أحدهما والتعادل - ماذا يمكننا أن نقول عن بعض الخطوط هناك)، ما عليك سوى إلقاء نظرة على الصورة:

تحديد الفهارس لخلايا المصفوفة

ماذا يحدث؟ إذا وضعنا نظام الإحداثيات القياسي $OXY$ في الزاوية اليسرى العليا وقمنا بتوجيه المحاور بحيث تغطي المصفوفة بأكملها، فيمكن ربط كل خلية من هذه المصفوفة بشكل فريد بالإحداثيات $\left(x;y \right) $ - سيكون هذا رقم الصف ورقم العمود.

لماذا يتم وضع نظام الإحداثيات في الزاوية اليسرى العليا بالضبط؟ نعم، لأنه من هناك نبدأ في قراءة أي نصوص. من السهل جدًا أن تتذكرها.

لماذا يشير المحور $x$ إلى الأسفل وليس إلى اليمين؟ مرة أخرى، الأمر بسيط: خذ نظام الإحداثيات القياسي (يتجه المحور $x$ إلى اليمين، ويتجه المحور $y$ إلى الأعلى) وقم بتدويره بحيث يحيط بالمصفوفة. وهذا دوران بمقدار 90 درجة في اتجاه عقارب الساعة - ونرى نتيجته في الصورة.

بشكل عام، اكتشفنا كيفية تحديد مؤشرات عناصر المصفوفة. الآن دعونا نتعامل مع الضرب.

تعريف. المصفوفات $A=\left[ m\times n \right]$ و $B=\left[ n\times k \right]$، عندما يتطابق عدد الأعمدة في الأول مع عدد الصفوف في الثانية، هي دعا متسقة.

إنه بهذا الترتيب. يمكن للمرء أن يكون غامضًا ويقول إن المصفوفات $A$ و$B$ تشكل زوجًا مرتبًا $\left(A;B \right)$: إذا كانت متسقة بهذا الترتيب، فليس من الضروري على الإطلاق أن يكون $B $ و$A$، هؤلاء. الزوج $\left(B;A \right)$ ثابت أيضًا.

يمكن ضرب المصفوفات المتسقة فقط.

تعريف. حاصل ضرب المصفوفات المتسقة $A=\left[ m\times n \right]$ و $B=\left[ n\times k \right]$ هو المصفوفة الجديدة $C=\left[ m\times k \right ]$ ، والتي يتم حساب عناصرها $((c)_(ij))$ بالصيغة:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

بمعنى آخر: للحصول على العنصر $((c)_(ij))$ من المصفوفة $C=A\cdot B$، عليك أن تأخذ الصف $i$-من المصفوفة الأولى، $j$ -العمود من المصفوفة الثانية، ثم قم بضرب العناصر من هذا الصف والعمود في أزواج. قم بإضافة النتائج.

نعم، هذا تعريف قاس. عدة حقائق تتبع على الفور:

ضرب المصفوفة، بشكل عام، غير تبادلي: $A\cdot B\ne B\cdot A$;
ومع ذلك، الضرب هو ترابطي: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
وحتى التوزيع: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
والتوزيع مرة أخرى: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

كان لا بد من وصف توزيع الضرب بشكل منفصل لمجموع المضاعف الأيسر والأيمن فقط بسبب عدم تبادلية عملية الضرب.

ومع ذلك، إذا تبين أن $A\cdot B=B\cdot A$، فإن هذه المصفوفات تسمى قابلة للتغيير.

من بين جميع المصفوفات التي يتم ضربها بشيء هناك، هناك مصفوفات خاصة - تلك التي، عند ضربها في أي مصفوفة $A$، تعطي مرة أخرى $A$:

تعريف. تسمى المصفوفة $E$ بالهوية إذا كان $A\cdot E=A$ أو $E\cdot A=A$. في حالة المصفوفة المربعة $A$ يمكننا أن نكتب:

تعتبر مصفوفة الهوية ضيفًا متكررًا في حل معادلات المصفوفات. وبشكل عام ضيف متكرر في عالم المصفوفات. :)

وبسبب هذا $E$، جاء شخص ما باللعبة التي سيتم كتابتها بعد ذلك.

ما هي المصفوفة العكسية

نظرًا لأن ضرب المصفوفات عملية تستغرق وقتًا طويلاً للغاية (عليك مضاعفة مجموعة من الصفوف والأعمدة)، فإن مفهوم المصفوفة العكسية ليس أيضًا الأكثر تافهة. والأمر يحتاج إلى بعض التوضيح.

تعريف المفتاح

حسنا، حان الوقت لمعرفة الحقيقة.

تعريف. المصفوفة $B$ تسمى معكوس المصفوفة $A$ if

يُشار إلى المصفوفة العكسية بـ $((A)^(-1))$ (يجب عدم الخلط بينه وبين الدرجة!)، لذلك يمكن إعادة كتابة التعريف على النحو التالي:

يبدو أن كل شيء بسيط للغاية وواضح. ولكن عند تحليل مثل هذا التعريف، تطرح على الفور عدة أسئلة:

هل توجد مصفوفة معكوسة دائمًا؟ وإذا لم يكن دائما، فكيف تحدد: متى يكون موجودا، ومتى لا يكون؟
ومن قال أن مثل هذه المصفوفة هي بالضبط واحدة؟ ماذا لو كان هناك مجموعة كاملة من المعكوسات لبعض المصفوفات الأصلية $A$؟
كيف تبدو كل هذه "الانتكاسات"؟ وكيف تحسبهم في الواقع؟

أما بالنسبة لخوارزميات الحساب - فسنتحدث عن هذا بعد قليل. لكن سنجيب على بقية الأسئلة الآن. دعونا نرتبها في شكل تأكيدات منفصلة.

الخصائص الأساسية

لنبدأ بالشكل الذي يجب أن تبدو عليه المصفوفة $A$ حتى تحتوي على $((A)^(-1))$. الآن سوف نتأكد من أن كلا المصفوفتين يجب أن تكونا مربعتين، وبنفس الحجم: $\left[ n\times n \right]$.

ليما 1. بالنظر إلى المصفوفة $A$ ومعكوسها $((A)^(-1))$. إذن كلتا المصفوفتين مربعتان ولهما نفس الترتيب $n$.

دليل. كل شيء بسيط. اجعل المصفوفة $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. بما أن المنتج $A\cdot ((A)^(-1))=E$ موجود حسب التعريف، فإن المصفوفات $A$ و$((A)^(-1))$ متسقة بهذا الترتيب:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( محاذاة)\]

هذه نتيجة مباشرة لخوارزمية ضرب المصفوفة: المعاملان $n$ و$a$ هما "عبور" ويجب أن يكونا متساويين.

في الوقت نفسه، يتم تعريف الضرب العكسي أيضًا: $((A)^(-1))\cdot A=E$، وبالتالي فإن المصفوفات $((A)^(-1))$ و$A$ هي متسقة أيضًا في هذا الترتيب:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( محاذاة)\]

وبالتالي، دون فقدان العمومية، يمكننا أن نفترض أن $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. ومع ذلك، وفقًا لتعريف $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$، فإن أبعاد المصفوفات هي نفسها تمامًا:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

لذلك اتضح أن المصفوفات الثلاث - $A$، $((A)^(-1))$ و $E$ - مربعة الحجم $\left[ n\times n \right]$. تم إثبات الليما.

حسنا، هذا جيد بالفعل. نرى أن المصفوفات المربعة فقط هي التي يمكن عكسها. الآن دعونا نتأكد من أن المصفوفة العكسية هي نفسها دائمًا.

ليما 2. بالنظر إلى المصفوفة $A$ ومعكوسها $((A)^(-1))$. إذن هذه المصفوفة العكسية فريدة من نوعها.

دليل. لنبدأ من العكس: دع المصفوفة $A$ تحتوي على حالتين من المعكوسات على الأقل - $B$ و$C$. ومن ثم، وفقا للتعريف، فإن المساواة التالية صحيحة:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \النهاية(محاذاة)\]

من Lemma 1 نستنتج أن المصفوفات الأربع $A$ و$B$ و$C$ و$E$ هي مربعات بنفس الترتيب: $\left[ n\times n \right]$. ولذلك يتم تعريف المنتج:

بما أن ضرب المصفوفات عملية ترابطية (ولكنها ليست تبادلية!)، فيمكننا أن نكتب:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \النهاية(محاذاة)\]

لقد حصلنا على الخيار الوحيد الممكن: نسختان من المصفوفة العكسية متساويتان. تم إثبات الليما.

المنطق أعلاه يكرر حرفيًا تقريبًا إثبات تفرد العنصر العكسي لجميع الأعداد الحقيقية $b\ne 0$. الإضافة المهمة الوحيدة هي مراعاة أبعاد المصفوفات.

ومع ذلك، ما زلنا لا نعرف شيئًا عما إذا كانت أي مصفوفة مربعة قابلة للعكس. هنا يأتي المحدد لمساعدتنا - وهذه خاصية أساسية لجميع المصفوفات المربعة.

ليما 3 . نظرا لمصفوفة $A$. إذا كانت المصفوفة $((A)^(-1))$ معكوسًا لها موجودة، فإن محدد المصفوفة الأصلية يكون غير صفر:

\[\يسار| أ \يمين|\ني 0\]

دليل. نحن نعلم بالفعل أن $A$ و$((A)^(-1))$ عبارة عن مصفوفات مربعة بحجم $\left[ n\times n \right]$. لذلك، يمكن حساب المحدد لكل واحد منهم: $\left| أ \يمين|$ و$\يسار| ((أ)^(-1)) \اليمين|$. ومع ذلك، فإن محدد المنتج يساوي منتج المحددات:

\[\يسار| أ\cdot ب \يمين|=\يسار| \يمين|\cdot \يسار| ب \يمين|\يمين السهم \يسار| A\cdot ((A)^(-1)) \right|=\left| \يمين|\cdot \يسار| ((أ)^(-1)) \اليمين|\]

ولكن وفقًا لتعريف $A\cdot ((A)^(-1))=E$، فإن محدد $E$ يساوي دائمًا 1، لذلك

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \اليسار| A\cdot ((A)^(-1)) \right|=\left| E\يمين|; \\ & \اليسار| \يمين|\cdot \يسار| ((أ)^(-1)) \يمين|=1. \\ \النهاية(محاذاة)\]

حاصل ضرب رقمين يساوي واحدًا فقط إذا كان كل رقم من هذه الأرقام مختلفًا عن الصفر:

\[\يسار| أ \يمين|\ني 0;\رباعية \يسار| ((A)^(-1)) \right|\ne 0.\]

لذلك اتضح أن $\left| \right|\ne 0$. تم إثبات الليما.

في الواقع، هذا المطلب منطقي تمامًا. سنقوم الآن بتحليل الخوارزمية للعثور على المصفوفة العكسية - وسيصبح من الواضح تمامًا لماذا، من حيث المبدأ، لا يمكن أن توجد مصفوفة معكوسة بمحدد صفري.

لكن أولاً، دعونا نقوم بصياغة تعريف "مساعد":

تعريف. المصفوفة المنحلة هي مصفوفة مربعة الحجم $\left[ n\times n \right]$ ومحددها صفر.

وبالتالي، يمكننا التأكيد على أن أي مصفوفة قابلة للعكس هي غير متحللة.

كيفية العثور على المصفوفة العكسية

الآن سننظر في خوارزمية عالمية للعثور على المصفوفات العكسية. بشكل عام، هناك خوارزميتان مقبولتان بشكل عام، وسننظر أيضًا في الخوارزمية الثانية اليوم.

المصفوفة التي سيتم النظر فيها الآن فعالة جدًا للمصفوفات ذات الحجم $\left[ 2\times 2 \right]$ و- جزئيًا - ذات الحجم $\left[ 3\times 3 \right]$. لكن بدءًا من الحجم $\left[ 4\times 4 \right]$ فمن الأفضل عدم استخدامه. لماذا - الآن سوف تفهم كل شيء.

الإضافات الجبرية

إستعد. الآن سيكون هناك ألم. لا، لا تقلق: ممرضة جميلة ترتدي تنورة، جوارب من الدانتيل لن تأتي إليك ولن تعطيك حقنة في الأرداف. كل شيء أكثر واقعية: الإضافات الجبرية وصاحبة الجلالة "مصفوفة الاتحاد" تأتي إليك.

لنبدأ مع الرئيسي. يجب أن تكون هناك مصفوفة مربعة بالحجم $A=\left[ n\times n \right]$ وعناصرها مسماة $((a)_(ij))$. ومن ثم، لكل عنصر من هذا القبيل، يمكن تحديد مكمل جبري:

تعريف. المكمل الجبري $((A)_(ij))$ للعنصر $((a)_(ij))$ في الصف $i$-th والعمود $j$-th من المصفوفة $A=\left [ n \times n \right]$ عبارة عن بناء للنموذج

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

حيث $M_(ij)^(*)$ هو محدد المصفوفة التي تم الحصول عليها من $A$ الأصلي عن طريق حذف نفس الصف $i$-th والعمود $j$-th.

مرة أخرى. تتم الإشارة إلى المكمل الجبري لعنصر المصفوفة بالإحداثيات $\left(i;j \right)$ كـ $((A)_(ij))$ ويتم حسابه وفقًا للمخطط:

أولاً، نقوم بحذف الصف $i$- والعمود $j$-th من المصفوفة الأصلية. لقد حصلنا على مصفوفة مربعة جديدة، ونشير إلى محددها بالرمز $M_(ij)^(*)$.
ثم نضرب هذا المحدد في $((\left(-1 \right))^(i+j))$ - في البداية قد يبدو هذا التعبير مذهلًا، ولكن في الواقع اكتشفنا العلامة الموجودة أمام $ م_(ي)^(*) $.
نحن نحسب - نحصل على رقم محدد. أولئك. فالإضافة الجبرية هي مجرد رقم، وليست مصفوفة جديدة، وهكذا.

المصفوفة $M_(ij)^(*)$ نفسها تسمى الثانوية التكميلية للعنصر $((a)_(ij))$. وبهذا المعنى، فإن التعريف أعلاه للمكمل الجبري هو حالة خاصة لتعريف أكثر تعقيدًا - وهو التعريف الذي تناولناه في الدرس حول المحدد.

ملاحظة مهمة. في الواقع، في الرياضيات "للبالغين"، يتم تعريف الإضافات الجبرية على النحو التالي:

نحن نأخذ صفوف $k$ وأعمدة $k$ في مصفوفة مربعة. عند تقاطعهما، نحصل على مصفوفة بالحجم $\left[ k\times k \right]$ - يُطلق على محددها اسم ثانوي من الرتبة $k$ ويُشار إليه بالرمز $((M)_(k))$.

ثم نقوم بشطب هذه الصفوف $k$ "المحددة" والأعمدة $k$. مرة أخرى، حصلنا على مصفوفة مربعة - محددها يسمى المصفوفة التكميلية الصغيرة ويرمز لها بـ $M_(k)^(*)$.

اضرب $M_(k)^(*)$ في $((\left(-1 \right))^(t))$، حيث $t$ هو (انتبه الآن!) مجموع أرقام جميع الصفوف المحددة والأعمدة . ستكون هذه الإضافة الجبرية.

ألقِ نظرة على الخطوة الثالثة: يوجد بالفعل مبلغ قدره 2 ألف دولار! شيء آخر هو أنه بالنسبة إلى $k=1$ نحصل على حدين فقط - سيكونان نفس $i+j$ - "إحداثيات" العنصر $((a)_(ij))$، الذي نحن عليه أبحث عن مكمل جبري.

لذلك نستخدم اليوم تعريفًا مبسطًا بعض الشيء. ولكن كما سنرى لاحقا، سيكون أكثر من كاف. والأهم من ذلك بكثير هو ما يلي:

تعريف. المصفوفة الموحدة $S$ إلى المصفوفة المربعة $A=\left[ n\times n \right]$ هي مصفوفة جديدة بالحجم $\left[ n\times n \right]$، والتي تم الحصول عليها من $A$ عن طريق استبدال $(( a)_(ij))$ بالمكملات الجبرية $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( أ)_(21)) & ((أ)_(22)) & ... & ((أ)_(2ن)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrix) \right]\]

الفكرة الأولى التي تطرأ في لحظة إدراك هذا التعريف هي "هذا هو المبلغ الإجمالي الذي يجب عليك حسابه!" الاسترخاء: عليك أن تحسب، ولكن ليس كثيرا. :)

حسنًا، كل هذا جميل جدًا، لكن لماذا هو ضروري؟ لكن لماذا.

النظرية الرئيسية

دعونا نعود قليلا. تذكر أن Lemma 3 ذكر أن المصفوفة القابلة للعكس $A$ تكون دائمًا غير مفردة (أي أن محددها غير صفر: $\left| A \right|\ne 0$).

لذا، فإن العكس صحيح أيضًا: إذا كانت المصفوفة $A$ غير متدهورة، فهي دائمًا قابلة للعكس. ويوجد أيضًا نظام بحث $((A)^(-1))$. تحقق من ذلك:

نظرية المصفوفة العكسية. لنفترض أن المصفوفة المربعة $A=\left[ n\times n \right]$ محددة، ومحددها غير صفر: $\left| \right|\ne 0$. ثم توجد المصفوفة العكسية $((A)^(-1))$ ويتم حسابها بالصيغة:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

والآن - كل نفس، ولكن بخط واضح. للعثور على المصفوفة العكسية، تحتاج إلى:

احسب المحدد $\left| A \right|$ وتأكد من أنها غير صفرية.
قم بتجميع مصفوفة الاتحاد $S$، أي. أحسب 100500 إضافة جبرية $((A)_(ij))$ ووضعها في مكانها $((a)_(ij))$.
قم بتبديل هذه المصفوفة $S$ ثم اضربها ببعض الأرقام $q=(1)/(\left| A \right|)\;$.

وهذا كل شيء! تم العثور على المصفوفة العكسية $((A)^(-1))$. دعونا نلقي نظرة على الأمثلة:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right]\]

حل. دعونا نتحقق من إمكانية الرجوع. دعونا نحسب المحدد:

\[\يسار| \يمين|=\يسار| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

المحدد يختلف عن الصفر. لذا فإن المصفوفة قابلة للعكس. لنقم بإنشاء مصفوفة اتحادية:

دعونا نحسب الإضافات الجبرية:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\اليمين|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\يمين|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \يمين|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\صحيح|=3. \\ \النهاية(محاذاة)\]

انتبه: المحددات |2|، |5|، |1| و |3| هي محددات المصفوفات ذات الحجم $\left[ 1\times 1 \right]$، وليست وحدات. أولئك. إذا كانت هناك أرقام سلبية في المحددات، فليس من الضروري إزالة "الطرح".

في المجمل، تبدو مصفوفة الاتحاد لدينا كما يلي:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (صفيف)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]\]

حسنًا، لقد انتهى كل شيء الآن. تم حل المشكلة.

إجابة. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

مهمة. أوجد المصفوفة العكسية:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

حل. مرة أخرى، نعتبر المحدد:

\[\begin(محاذاة) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matrix) ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

المحدد يختلف عن الصفر — المصفوفة قابلة للعكس. ولكن الآن سيكون الأمر الأكثر صغرًا: عليك أن تعد ما يصل إلى 9 (تسعة، اللعنة!) إضافات جبرية. وسيحتوي كل واحد منهم على $\left[ 2\times 2 \right]$ المؤهل. طار:

\[\begin(matrix) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrix) 2 & -1 \\ 0 & 1 \\\end(matrix) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\end(matrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrix) 1 & -1 \\ 0 & 2 \\\end(matrix) \right|=2; \\ \النهاية(مصفوفة)\]

باختصار، ستبدو مصفوفة الاتحاد كما يلي:

وبالتالي فإن المصفوفة العكسية ستكون:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(صفيف) \right]\]

حسنا هذا كل شيء. هنا هو الجواب.

إجابة. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

كما ترون، في نهاية كل مثال، قمنا بإجراء فحص. وفي هذا الصدد ملاحظة مهمة:

لا تكن كسولًا للتحقق. اضرب المصفوفة الأصلية في المعكوس الذي تم العثور عليه - يجب أن تحصل على $E$.

يعد إجراء هذا الفحص أسهل وأسرع بكثير من البحث عن خطأ في العمليات الحسابية الإضافية، عندما تقوم، على سبيل المثال، بحل معادلة مصفوفة.

طريقة بديلة

كما قلت، تعمل نظرية المصفوفة العكسية بشكل جيد مع الأحجام $\left[ 2\times 2 \right]$ و $\left[ 3\times 3 \right]$ (في الحالة الأخيرة، لم تعد "جميلة" بعد الآن ).")، ولكن بالنسبة للمصفوفات الكبيرة، يبدأ الحزن.

لكن لا تقلق: هناك خوارزمية بديلة يمكن استخدامها للعثور على المعكوس بهدوء حتى بالنسبة للمصفوفة $\left[ 10\times 10 \right]$. ولكن، كما هو الحال غالبًا، للنظر في هذه الخوارزمية، نحتاج إلى القليل من الخلفية النظرية.

التحولات الأولية

من بين التحولات المختلفة للمصفوفة، هناك العديد من التحولات الخاصة - تسمى الابتدائية. هناك بالضبط ثلاثة من هذه التحولات:

عمليه الضرب. يمكنك أخذ الصف (العمود) $i$-th وضربه بأي رقم $k\ne 0$;
إضافة. أضف إلى الصف (العمود) $i$-th أي صف (عمود) $j$-th آخر مضروبًا في أي رقم $k\ne 0$ (بالطبع، $k=0$ ممكن أيضًا، ولكن ما المغزى من ذلك؟ من ذلك؟ رغم ذلك لن يتغير شيء).
التقليب. خذ الصفوف (الأعمدة) $i$-th و $j$-th وقم بتبديلها.

لماذا تسمى هذه التحولات أولية (بالنسبة للمصفوفات الكبيرة لا تبدو أولية جدًا) ولماذا يوجد ثلاثة منها فقط - هذه الأسئلة خارج نطاق درس اليوم. ولذلك لن ندخل في التفاصيل.

شيء آخر مهم: علينا إجراء كل هذه الانحرافات على المصفوفة المرتبطة. نعم، نعم، لقد سمعت الحق. الآن سيكون هناك تعريف آخر - الأخير في درس اليوم.

المصفوفة المرفقة

من المؤكد أنك قمت في المدرسة بحل أنظمة المعادلات باستخدام طريقة الجمع. حسنًا ، اطرح سطرًا آخر من سطر واحد ، واضرب سطرًا ما برقم - هذا كل شيء.

لذلك: الآن سيكون كل شيء هو نفسه، ولكن بالفعل "كشخص بالغ". مستعد؟

تعريف. اسمح للمصفوفة $A=\left[ n\times n \right]$ ومصفوفة الهوية $E$ بنفس الحجم $n$ أن تعطى. ثم المصفوفة المرتبطة $\left[ A\left| ه\صحيح. \right]$ عبارة عن مصفوفة $\left[ n\times 2n \right]$ جديدة تبدو كما يلي:

\[\left[ A\left| ه\صحيح. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((أ)_(21)) & ((أ)_(22)) & ... & ((أ)_(2ن)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... \\((أ)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

باختصار، نأخذ المصفوفة $A$، على اليمين نخصص لها مصفوفة الهوية $E$ بالحجم المطلوب، ونفصلها بشريط عمودي للجمال - هذا هو المرفق. :)

ما الفائدة؟ وهذا ما:

نظرية. دع المصفوفة $A$ تكون قابلة للعكس. خذ بعين الاعتبار المصفوفة المجاورة $\left[ A\left| ه\صحيح. \يمين]$. في حالة استخدام تحويلات السلسلة الأوليةأحضره إلى النموذج $\left[ E\left| ساطع. \right]$، أي عن طريق ضرب الصفوف وطرحها وإعادة ترتيبها للحصول على المصفوفة $E$ من $A$ على اليمين، ثم المصفوفة $B$ التي تم الحصول عليها على اليسار هي معكوس $A$:

\[\left[ A\left| ه\صحيح. \يمين]\إلى \يسار[ E\يسار| ساطع. \right]\Rightarrow B=((A)^(-1))\]

بكل بساطة! باختصار، تبدو خوارزمية العثور على المصفوفة العكسية كما يلي:

اكتب المصفوفة المرتبطة $\left[ A\left| ه\صحيح. \يمين]$;
قم بإجراء تحويلات السلسلة الأولية حتى يظهر اليمين بدلاً من $A$ $E$؛
بالطبع، سيظهر أيضًا شيء ما على اليسار - مصفوفة معينة $B$. وسيكون هذا هو العكس.
الأرباح! :)

وبطبيعة الحال، القول أسهل بكثير من الفعل. لذلك دعونا نلقي نظرة على بعض الأمثلة: بالنسبة للأحجام $\left[ 3\times 3 \right]$ و$\left[ 4\times 4 \right]$.

مهمة. أوجد المصفوفة العكسية:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

حل. نقوم بتكوين المصفوفة المرفقة:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(صفيف) \يمين]\]

بما أن العمود الأخير من المصفوفة الأصلية مليء بالآحاد، اطرح الصف الأول من الباقي:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\\end(matrix)\to \\ & \to \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(صفيف) \يمين] \\ \end(محاذاة)\]

لا توجد وحدات أخرى، باستثناء السطر الأول. لكننا لا نلمسها، وإلا فإن الوحدات التي تمت إزالتها حديثا ستبدأ في "الضرب" في العمود الثالث.

لكن يمكننا طرح السطر الثاني مرتين من السطر الأخير - نحصل على وحدة في الزاوية اليسرى السفلية:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(صفيف) \يمين]\begin(matrix) \ \\ \downarrow \\ -2 \\\end(matrix)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(صفيف) \يمين] \\ \end(محاذاة)\]

يمكننا الآن طرح الصف الأخير من الأول ومرتين من الثاني - وبهذه الطريقة سنحذف العمود الأول:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) -1 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \ إلى \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(صفيف) \يمين] \\ \end(محاذاة)\]

اضرب الصف الثاني في −1 ثم اطرحه 6 مرات من الأول وأضف مرة واحدة إلى الأخير:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) -6 \\ \updownarrow \\ +1 \\\end (مصفوفة)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(صفيف) \يمين] \\ \end(محاذاة)\]

يبقى فقط لمبادلة السطرين 1 و 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 و 32 و -13 \\\end(صفيف) \يمين]\]

مستعد! على اليمين توجد المصفوفة العكسية المطلوبة.

إجابة. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

مهمة. أوجد المصفوفة العكسية:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(مصفوفة) \يمين]\]

حل. مرة أخرى نكتب المرفق:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

دعنا نقترض قليلاً، ونقلق بشأن المبلغ الذي يتعين علينا أن نحسبه الآن... ونبدأ في العد. للبدء، نقوم "بتصفية" العمود الأول عن طريق طرح الصف 1 من الصفين 2 و3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(صفيف) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

نلاحظ الكثير من "السلبيات" في السطور 2-4. اضرب جميع الصفوف الثلاثة في −1، ثم احرق العمود الثالث عن طريق طرح الصف 3 من الباقي:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \يسار| \cdot \left(-1 \right) \right. \\ \يسار| \cdot \left(-1 \right) \right. \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (array) \right]\begin(matrix) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matrix)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

حان الآن وقت "قلي" العمود الأخير من المصفوفة الأصلية: اطرح الصف 4 من الباقي:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(صفيف ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

اللفة النهائية: "حرق" العمود الثاني عن طريق طرح الصف 2 من الصف 1 و 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( array) \right]\begin(matrix) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

ومرة أخرى، مصفوفة الهوية على اليسار، وبالتالي المعكوس على اليمين. :)

إجابة. $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(مصفوفة) \يمين]$

حسنًا، لقد انتهى كل شيء الآن. قم بالفحص بنفسك - لقد ألغيت. :)

الإضافات الجبرية والقصر

لنحصل على محدد من الدرجة الثالثة: .

صغيرالمقابلة لهذا العنصر aijالمحدد من الدرجة الثالثة هو المحدد من الدرجة الثانية الذي يتم الحصول عليه من المحدد المحدد عن طريق حذف الصف والعمود عند التقاطع الذي يقف عنده العنصر المحدد، أي. أنا- السطر و ي- العمود. القصر المقابلة لعنصر معين aijسوف نشير م ج.

على سبيل المثال، صغير م12المقابلة للعنصر 12، سيكون هناك محدد 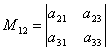، والتي يتم الحصول عليها عن طريق حذف الصف الأول والعمود الثاني من المحدد المحدد.

وبالتالي، فإن الصيغة التي تحدد محدد الدرجة الثالثة توضح أن هذا المحدد يساوي مجموع منتجات عناصر الصف الأول والعناصر الثانوية المقابلة لها؛ في حين أن القاصر يتوافق مع العنصر 12، مأخوذة بعلامة "-" ، أي. يمكن كتابة ذلك

(1)

وبالمثل، يمكن تقديم تعريفات للقصر لمحددات الدرجة الثانية والرتب العليا.

دعونا نقدم مفهوما آخر.

إضافة جبريةعنصر aijويسمى المحدد قاصر م جمضروبًا في (–1) i+j .

إضافة العناصر الجبرية aijيعني ا ج.

من التعريف نحصل على أن العلاقة بين المكمل الجبري للعنصر وقاصره يتم التعبير عنها بالمساواة ا ج= (–1) ط+ي م ي .

على سبيل المثال،

مثال.نظرا لمحدد. يجد أ 13، أ 21، أ 32.

من السهل أن نرى أنه باستخدام الإضافات الجبرية للعناصر، يمكن كتابة الصيغة (1) على النحو التالي:

وبالمثل لهذه الصيغة، يمكن الحصول على تحليل المحدد على عناصر أي صف أو عمود.

على سبيل المثال، يمكن الحصول على تحلل المحدد على عناصر الصف الثاني على النحو التالي. حسب الخاصية 2 للمحدد لدينا :

دعونا نوسع المحدد الذي تم الحصول عليه بعناصر الصف الأول.

(2)

من هنا لأن المحددات من الدرجة الثانية في الصيغة (2) هي العناصر الثانوية أ 21، أ 22، أ 23. وهكذا، أي. لقد حصلنا على توسيع المحدد بعناصر الصف الثاني.

وبالمثل، يمكن الحصول على تحليل المحدد على عناصر الصف الثالث. باستخدام الخاصية 1 للمحددات (عند التبديل)، يمكن للمرء أن يوضح أن التوسعات المماثلة صالحة أيضًا للتوسعات في عناصر العمود.

وبالتالي فإن النظرية التالية صحيحة.

نظرية (على توسيع المحدد في صف أو عمود معين).المحدد يساوي مجموع منتجات عناصر أي من صفوفه (أو أعمدةه) ومكملاتها الجبرية.

كل ما سبق ينطبق على المحددات من أي ترتيب أعلى.

أمثلة.

المصفوفة العكسية

تم تقديم مفهوم المصفوفة العكسية فقط ل المصفوفات المربعة.

لو أهي مصفوفة مربعة، إذن يعكسبالنسبة لها، المصفوفة هي مصفوفة يشار إليها أ-1واستيفاء الشرط . (يتم تقديم هذا التعريف قياسا على ضرب الأعداد)

تُسمى المصفوفة $A^(-1)$ بعكس المصفوفة المربعة $A$ إذا كانت $A^(-1)\cdot A=A\cdot A^(-1)=E$، حيث $E $ هي مصفوفة الهوية، ترتيبها يساوي ترتيب المصفوفة $A$.

المصفوفة غير المفردة هي مصفوفة لا يساوي محددها الصفر. وبناء على ذلك، فإن المصفوفة المنحلة هي تلك التي يكون محددها يساوي الصفر.

المصفوفة العكسية $A^(-1)$ موجودة فقط إذا كانت المصفوفة $A$ غير مفردة. إذا كانت المصفوفة العكسية $A^(-1)$ موجودة، فهي فريدة من نوعها.

هناك عدة طرق للعثور على معكوس المصفوفة، وسننظر في اثنتين منها. ستناقش هذه الصفحة طريقة المصفوفة المجاورة، والتي تعتبر معيارًا في معظم دورات الرياضيات العليا. أما الطريقة الثانية لإيجاد المصفوفة العكسية (طريقة التحويلات الأولية) والتي تتضمن استخدام طريقة غاوس أو طريقة غاوس-جوردان فقد تناولناها في الجزء الثاني.

طريقة المصفوفة المجاورة (الاتحاد).

دع المصفوفة $A_(n\times n)$ تعطى. من أجل العثور على المصفوفة العكسية $A^(-1)$، يلزم ثلاث خطوات:

ابحث عن محدد المصفوفة $A$ وتأكد من أن $\Delta A\neq 0$، أي. أن المصفوفة A غير متحللة.
قم بتكوين المكملات الجبرية $A_(ij)$ لكل عنصر من عناصر المصفوفة $A$ واكتب المصفوفة $A_(n\times n)^(*)=\left(A_(ij) \right)$ من الموجود المكملات الجبرية.
اكتب المصفوفة العكسية مع مراعاة الصيغة $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*)^T$.

غالبًا ما يشار إلى المصفوفة $(A^(*))^T$ على أنها المصفوفة المجاورة (المتبادلة والمتحالفة) لـ $A$.

إذا تم اتخاذ القرار يدويًا، فإن الطريقة الأولى تكون جيدة فقط لمصفوفات الطلبات الصغيرة نسبيًا: الثانية ()، الثالثة ()، الرابعة (). للعثور على المصفوفة العكسية لمصفوفة ذات ترتيب أعلى، يتم استخدام طرق أخرى. على سبيل المثال، طريقة غاوس، والتي تمت مناقشتها في الجزء الثاني.

مثال 1

ابحث عن المصفوفة المعكوسة للمصفوفة $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

بما أن جميع عناصر العمود الرابع تساوي الصفر، فإن $\Delta A=0$ (أي أن المصفوفة $A$ تتدهور). بما أن $\Delta A=0$، فلا يوجد مصفوفة معكوسة لـ $A$.

إجابة: المصفوفة $A^(-1)$ غير موجودة.

مثال رقم 2

أوجد المصفوفة المعكوسة للمصفوفة $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. قم بإجراء فحص.

نحن نستخدم طريقة المصفوفة المجاورة. أولاً، دعونا نوجد محدد المصفوفة المعطاة $A$:

$$ \دلتا أ=\يسار| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

بما أن $\Delta A \neq 0$، فإن المصفوفة العكسية موجودة، لذلك نواصل الحل. إيجاد المكملات الجبرية

\begin(محاذاة) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(محاذاة)

أنشئ مصفوفة من المكملات الجبرية: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

تبديل المصفوفة الناتجة: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (الناتج غالبًا ما تسمى المصفوفة بالمصفوفة المجاورة أو الموحدة للمصفوفة $A$). باستخدام الصيغة $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$، لدينا:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

لذلك تم العثور على المصفوفة العكسية: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \صحيح) $. للتحقق من صحة النتيجة، يكفي التحقق من صحة إحدى المعادلتين: $A^(-1)\cdot A=E$ أو $A\cdot A^(-1)=E$. دعونا نتحقق من المساواة $A^(-1)\cdot A=E$. لكي نتمكن من العمل بشكل أقل مع الكسور، سنستبدل المصفوفة $A^(-1)$ ليس بالشكل $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ ولكن كـ $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \ النهاية (مصفوفة )\يمين)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( صفيف)\يمين)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array )\يمين) =E $$

إجابة: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

مثال رقم 3

أوجد معكوس المصفوفة $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$. قم بإجراء فحص.

لنبدأ بحساب محدد المصفوفة $A$. إذن محدد المصفوفة $A$ هو:

$$ \دلتا أ=\يسار| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

بما أن $\Delta A\neq 0$، فإن المصفوفة العكسية موجودة، لذلك نواصل الحل. نجد المكملات الجبرية لكل عنصر من عناصر المصفوفة المعطاة:

نقوم بتكوين مصفوفة من الإضافات الجبرية ونقلها:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

باستخدام الصيغة $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$، نحصل على:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 و -3/26 و 37/26 \end(صفيف) \يمين) $$

إذن $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 و -3/26 و 37/26 \end(array) \right)$. للتحقق من صحة النتيجة، يكفي التحقق من صحة إحدى المعادلتين: $A^(-1)\cdot A=E$ أو $A\cdot A^(-1)=E$. دعونا نتحقق من المساواة $A\cdot A^(-1)=E$. لكي نتمكن من العمل بشكل أقل مع الكسور، سنستبدل المصفوفة $A^(-1)$ ليس بالشكل $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$، ولكن كـ $\frac(1)(26)\ cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \يمين)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ النهاية(صفيف) \يمين) =\frac(1)(26)\cdot\left(\begin(array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (صفيف) \يمين) =\left(\begin(array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

تم اجتياز الاختبار بنجاح، وتم العثور على المصفوفة العكسية $A^(-1)$ بشكل صحيح.

إجابة: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 و -3/26 و 37/26 \end(array) \right)$.

المثال رقم 4

ابحث عن معكوس المصفوفة $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

بالنسبة لمصفوفة من الدرجة الرابعة، فإن العثور على المصفوفة العكسية باستخدام الإضافات الجبرية أمر صعب إلى حد ما. ومع ذلك، توجد مثل هذه الأمثلة في أعمال التحكم.

للعثور على المصفوفة العكسية، عليك أولاً حساب محدد المصفوفة $A$. أفضل طريقة للقيام بذلك في هذه الحالة هي توسيع المحدد في صف (عمود). نختار أي صف أو عمود ونجد المكمل الجبري لكل عنصر في الصف أو العمود المحدد.

على سبيل المثال، بالنسبة للصف الأول نحصل على:

$$ A_(11)=\left|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\left|\begin(array)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\left|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

يتم حساب محدد المصفوفة $A$ بالصيغة التالية:

$$ \دلتا(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14) )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;أ_(43)=-463;\;أ_(44)=-96. \end(محاذاة) $$

المصفوفة التكميلية الجبرية: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 و -250 و -463 و -96\end(array)\right)$.

المصفوفة المرفقة: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

مصفوفة معكوسة:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 و 1/25 و 9/25 و -24/25 \end(صفيف) \يمين) $$

يمكن إجراء الفحص، إذا رغبت في ذلك، بنفس الطريقة كما في الأمثلة السابقة.

إجابة: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 و 87/100 و 83/100 و -463/100 \\ -28/25 و 1/25 و 9/25 و -24/25 \end(مصفوفة) \\ يمين) $.

وفي الجزء الثاني سنتناول طريقة أخرى لإيجاد المصفوفة العكسية والتي تتضمن استخدام تحويلات طريقة غاوس أو طريقة غاوس-جوردان.

دعونا نعطي مصفوفة مربعة. مطلوب العثور على المصفوفة العكسية.

الطريقة الأولى. في النظرية 4.1 حول وجود وتفرد المصفوفة العكسية، تمت الإشارة إلى إحدى طرق العثور عليها.

1. احسب محدد المصفوفة المعطاة. إذا، فإن المصفوفة العكسية غير موجودة (المصفوفة متدهورة).

2. تكوين مصفوفة من المكملات الجبرية لعناصر المصفوفة.

3. من خلال تبديل المصفوفة، احصل على المصفوفة المرتبطة بها .

4. أوجد المصفوفة العكسية (4.1) عن طريق قسمة جميع عناصر المصفوفة المرتبطة بها على المحدد

الطريقة الثانية. للعثور على المصفوفة العكسية، يمكن استخدام التحويلات الأولية.

1. قم بتكوين مصفوفة كتلة عن طريق تعيين مصفوفة هوية المصفوفة المحددة بنفس الترتيب.

2. بمساعدة التحولات الأولية التي يتم إجراؤها على صفوف المصفوفة، قم بإحضار الكتلة اليسرى إلى أبسط شكل. في هذه الحالة يتم اختزال المصفوفة الكتلية إلى الشكل، حيث يتم الحصول على مصفوفة مربعة نتيجة التحولات من مصفوفة الهوية.

3. إذا كانت الكتلة مساوية للمصفوفة العكسية، أي إذا، فإن المصفوفة ليس لها معكوس.

في الواقع، بمساعدة التحولات الأولية لصفوف المصفوفة، يمكن تقليل الكتلة اليسرى إلى شكل مبسط (انظر الشكل 1.5). وفي هذه الحالة تتحول المصفوفة الكتلية إلى الشكل حيث تكون مصفوفة أولية تحقق المساواة. إذا كانت المصفوفة غير مفردة، فوفقًا للبند 2 من الملاحظات 3.3، يتطابق شكلها المبسط مع مصفوفة الهوية. ثم يترتب على المساواة ذلك. إذا كانت المصفوفة منحلة، فإن شكلها المبسط يختلف عن مصفوفة الهوية، وليس للمصفوفة معكوس.

11. معادلات المصفوفة وحلها. شكل مصفوفة لكتابة SLAE. طريقة المصفوفة (طريقة المصفوفة العكسية) لحل SLAE وشروط تطبيقها.

معادلات المصفوفة هي معادلات بالشكل: A*X=C; X*أ=ج; A*X*B=C حيث المصفوفات A وB وC معروفة، والمصفوفة X غير معروفة، إذا لم تتحلل المصفوفات A وB، فسيتم كتابة حلول المصفوفات الأصلية بالشكل المقابل: X=أ -1 *ج; X=C*A -1; X \u003d أ -1 * ج * ب -1 شكل مصفوفة لأنظمة كتابة المعادلات الجبرية الخطية.يمكن ربط عدة مصفوفات بكل SLAE؛ علاوة على ذلك، يمكن كتابة SLAE نفسها كمعادلة مصفوفية. بالنسبة لـ SLAE (1)، ضع في اعتبارك المصفوفات التالية:

تسمى المصفوفة A مصفوفة النظام. عناصر هذه المصفوفة هي معاملات SLAE المحددة.

المصفوفة A˜ تسمى نظام المصفوفة الموسعة. ويتم الحصول عليه عن طريق إضافة عمود يحتوي على الأعضاء الأحرار b1,b2,...,bm إلى مصفوفة النظام. عادةً ما يتم فصل هذا العمود بخط عمودي من أجل الوضوح.

تسمى مصفوفة العمود B مصفوفة الأعضاء الأحرار، ومصفوفة العمود X هي مصفوفة المجهول.

باستخدام الترميز المقدم أعلاه، يمكن كتابة SLAE (1) في شكل معادلة مصفوفية: A⋅X=B.

ملحوظة

يمكن كتابة المصفوفات المرتبطة بالنظام بطرق مختلفة: كل شيء يعتمد على ترتيب المتغيرات والمعادلات الخاصة بـ SLAE المدروسة. ولكن على أية حال، فإن ترتيب المجهولات في كل معادلة لـ SLAE معين يجب أن يكون هو نفسه.

تعتبر طريقة المصفوفة مناسبة لحل SLAEs التي يتزامن فيها عدد المعادلات مع عدد المتغيرات المجهولة ويكون محدد المصفوفة الرئيسية للنظام غير صفر. إذا كان النظام يحتوي على أكثر من ثلاث معادلات، فإن العثور على المصفوفة العكسية يتطلب جهدًا حسابيًا كبيرًا، لذلك، في هذه الحالة، ينصح باستخدامها للحل طريقة غاوس.

12. SLAEs المتجانسة، شروط وجود حلولها غير الصفرية. خصائص الحلول الجزئية لـ SLAEs المتجانسة.

تسمى المعادلة الخطية متجانسة إذا كان حدها الحر يساوي صفرًا، وغير متجانسة إذا كان حدها الحر يساوي صفرًا. يسمى النظام الذي يتكون من معادلات متجانسة متجانسة وله الشكل العام:

13 مفهوم الاستقلال الخطي واعتماد الحلول الجزئية لـ SLAE المتجانسة. نظام القرار الأساسي (FSR) ونتائجه. تمثيل الحل العام لـ SLAE المتجانس من حيث FSR.

نظام الوظيفة ذ 1 (س ), ذ 2 (س ), …, ذ ن (س ) يسمى تعتمد خطيافي الفاصل ( أ , ب ) إذا كانت هناك مجموعة من المعاملات الثابتة التي لا تساوي الصفر في وقت واحد، بحيث تكون المجموعة الخطية لهذه الوظائف مساوية للصفر على ( أ , ب ): ل . إذا كانت المساواة ممكنة فقط بالنسبة لنظام الوظائف ذ 1 (س ), ذ 2 (س ), …, ذ ن (س ) يسمى مستقل خطيافي الفاصل ( أ , ب ). وبعبارة أخرى، الوظائف ذ 1 (س ), ذ 2 (س ), …, ذ ن (س ) تعتمد خطيافي الفاصل ( أ , ب ) إذا كان هناك صفر على ( أ , ب ) مجموعتهم الخطية غير تافهة. المهام ذ 1 (س ),ذ 2 (س ), …, ذ ن (س ) مستقل خطيافي الفاصل ( أ , ب ) إذا كانت مجموعتها الخطية التافهة تساوي الصفر على ( أ , ب ).

نظام القرار الأساسي (FSR) SLAE المتجانس هو أساس نظام الأعمدة هذا.

عدد العناصر في FSR يساوي عدد العناصر المجهولة في النظام مطروحًا منه رتبة مصفوفة النظام. أي حل للنظام الأصلي هو عبارة عن مجموعة خطية من حلول FSR.

نظرية

الحل العام لـ SLAE غير المتجانس يساوي مجموع الحل الخاص لـ SLAE غير المتجانس والحل العام لـ SLAE المتجانس المقابل.

1 . إذا كانت الأعمدة عبارة عن حلول لنظام متجانس من المعادلات، فإن أي مجموعة خطية منها هي أيضًا حل لنظام متجانس.

والواقع أنه يترتب على المساواة أن

أولئك. مجموعة خطية من الحلول هي الحل لنظام متجانس.

2. إذا كانت رتبة مصفوفة النظام المتجانس هي، فإن النظام لديه حلول مستقلة خطيا.

وبالفعل يمكننا من خلال الصيغ (5.13) للحل العام للنظام المتجانس إيجاد حلول خاصة بإسناد ما يلي للمتغيرات الحرة مجموعات القيمة الافتراضية (في كل مرة نفترض أن أحد المتغيرات الحرة يساوي واحدًا، والباقي يساوي صفرًا):

والتي تكون مستقلة خطيا. وبالفعل، إذا تم تكوين مصفوفة من هذه الأعمدة، فإن صفوفها الأخيرة تشكل مصفوفة الهوية. ولذلك فإن القاصر الموجود في الصفوف الأخيرة لا يساوي صفراً (إنه يساوي واحداً)، أي. أساسي. وبالتالي فإن رتبة المصفوفة ستكون متساوية. ومن ثم، فإن جميع أعمدة هذه المصفوفة مستقلة خطيًا (انظر النظرية 3.4).

تسمى أي مجموعة من الحلول المستقلة خطيا لنظام متجانس النظام الأساسي (مجموعة) من الحلول .

14 قاصر من المرتبة الرابعة، قاصر أساسي، رتبة مصفوفة. حساب رتبة المصفوفة.

الرتبة k الثانوية للمصفوفة A هي المحدد لبعض مصفوفاتها الفرعية المربعة من الرتبة k.

في مصفوفة m x n A، يُطلق على المصفوفة الثانوية من الرتبة r اسم أساسي إذا كانت غير صفرية، وجميع المصفوفات الثانوية من الرتبة الأكبر، إذا كانت موجودة، تساوي الصفر.

تسمى أعمدة وصفوف المصفوفة A، عند تقاطعها قاعدة ثانوية، بالأعمدة والصفوف الأساسية للمصفوفة A.

النظرية 1. (على رتبة المصفوفة). بالنسبة لأي مصفوفة، الرتبة الثانوية تساوي رتبة الصف وتساوي رتبة العمود.

النظرية 2. (في القاصر الأساسي). يتحلل كل عمود من أعمدة المصفوفة إلى مجموعة خطية من أعمدتها الأساسية.

رتبة المصفوفة (أو الرتبة الثانوية) هي ترتيب الأساس الثانوي أو، بمعنى آخر، الترتيب الأكبر الذي توجد به عناصر ثانوية غير الصفر. تعتبر رتبة المصفوفة الصفرية، حسب التعريف، 0.

نلاحظ خاصيتين واضحتين للرتبة الثانوية.

1) لا تتغير رتبة المصفوفة عند النقل، حيث أنه عند نقل المصفوفة، يتم نقل جميع مصفوفاتها الفرعية ولا تتغير العناصر الثانوية.

2) إذا كانت A' عبارة عن مصفوفة فرعية للمصفوفة A، فإن رتبة A' لا تتجاوز رتبة A، نظرًا لأن القاصر غير الصفري الموجود في A' يتم تضمينه أيضًا في A.

15. مفهوم المتجهات الحسابية ذات الأبعاد. المساواة المتجهات. الإجراءات على المتجهات (الجمع، الطرح، الضرب برقم، الضرب بمصفوفة). مزيج خطي من المتجهات.

جمع أمر نتسمى الأعداد الحقيقية أو المركبة ناقلات الأبعاد ن. يتم استدعاء الأرقام إحداثيات المتجهات.

متجهان (غير صفر). أو بتكون متساوية إذا كانت متساوية الاتجاه ولها نفس المعامل. جميع المتجهات الصفرية تعتبر متساوية. وفي جميع الحالات الأخرى، فإن المتجهات ليست متساوية.

إضافة ناقلات. هناك طريقتان لإضافة ناقلات.1. قاعدة متوازي الأضلاع. لجمع المتجهات و، نضع بدايات كل منهما في نفس النقطة. نكمل متوازي الأضلاع ونرسم قطري متوازي الأضلاع من نفس النقطة. سيكون هذا مجموع المتجهات.

2. الطريقة الثانية لإضافة المتجهات هي قاعدة المثلث. لنأخذ نفس المتجهات و . نضيف بداية الثانية إلى نهاية المتجه الأول. الآن دعونا نربط بداية الأول ونهاية الثانية. هذا هو مجموع المتجهات و . وبنفس القاعدة، يمكنك إضافة عدة ناقلات. نعلقها واحدة تلو الأخرى، ثم نربط بداية الأول بنهاية الأخير.

طرح المتجهات. يتم توجيه المتجه عكس المتجه. أطوال المتجهات متساوية. الآن أصبح من الواضح ما هو طرح المتجهات. الفرق بين المتجهات هو مجموع المتجه والمتجه.

ضرب المتجه برقم

يؤدي ضرب المتجه برقم k إلى الحصول على متجه يبلغ طوله k مرات مختلفة عن الطول. يكون اتجاهيًا مع المتجه إذا كانت k أكبر من الصفر، ويكون موجهًا بشكل معاكس إذا كانت k أقل من الصفر.

المنتج القياسي للمتجهات هو حاصل ضرب أطوال المتجهات وجيب تمام الزاوية بينهما.إذا كان المتجهان متعامدين، فإن حاصل ضربهما القياسي يساوي صفرًا. وهذه هي الطريقة التي يتم بها التعبير عن المنتج القياسي بدلالة إحداثيات المتجهات و .

مزيج خطي من المتجهات

مزيج خطي من المتجهات ناقلات المكالمة

أين - معاملات الجمع الخطية. لو ويسمى الجمع تافهًا إذا كان غير تافه.

16 .المنتج العددي للمتجهات الحسابية. طول المتجه والزاوية بين المتجهات. مفهوم تعامد المتجهات.

المنتج العددي للمتجهين a و b هو العدد

يتم استخدام المنتج القياسي لحساب: 1) إيجاد الزاوية بينهما؛ 2) إيجاد إسقاط المتجهات؛ 3) حساب طول المتجه؛ 4) شروط المتجهات المتعامدة.

طول القطعة AB هو المسافة بين النقطتين A وB. الزاوية بين المتجهين A و B تسمى الزاوية α = (a، c)، 0≥ α ≥П. ومن خلاله من الضروري تدوير متجه واحد بحيث يتزامن اتجاهه مع متجه آخر. بشرط أن تتزامن بداياتهما.

Orth a هو المتجه a الذي له وحدة طول واتجاه a.

17. نظام المتجهات ومجموعته الخطية. مفهوم الاعتماد الخطي واستقلال نظام المتجهات. نظرية الشروط الضرورية والكافية للاعتماد الخطي لنظام المتجهات.

يسمى نظام المتجهات a1,a2,...,an معتمدًا خطيًا إذا كان هناك أرقام π1,π2,...,ạn بحيث يكون واحد منها على الأقل غير صفر و π1a1+π2a2+...+ lectnan=0 . خلاف ذلك، يسمى النظام مستقل خطيا.

يُسمى المتجهان a1 وa2 على خط واحد إذا كان اتجاههما متماثلًا أو متضادًا.

تسمى المتجهات الثلاثة a1 وa2 وa3 متحدة المستوى إذا كانت موازية لمستوى ما.

المعايير الهندسية للاعتماد الخطي:

أ) يعتمد النظام (a1,a2) خطيًا إذا كان المتجهان a1 وa2 على خط واحد فقط.

ب) يعتمد النظام (a1,a2,a3) خطيًا فقط إذا كانت المتجهات a1 وa2 وa3 متحدة المستوى.

نظرية. (شرط ضروري وكاف للاعتماد الخطي أنظمةثلاثة أبعاد.)

نظام المتجهات المتجه فضاءيكون خطيالا يعتمد إلا إذا تم التعبير عن أحد متجهات النظام خطيًا بدلالة المتجهات الأخرى المتجههذا النظام.

النتيجة.1. يكون نظام المتجهات في الفضاء المتجه مستقلاً خطيًا إذا وفقط إذا لم يتم التعبير عن أي من متجهات النظام خطيًا من حيث المتجهات الأخرى لهذا النظام.2. يعتمد نظام المتجهات الذي يحتوي على ناقل صفري أو متجهين متساويين خطيًا.