Dom Internet

Inverzna matrica podataka i algoritam za njeno izračunavanje. Pronađite inverznu matricu na mreži

Originalni prema formuli: A^-1 = A*/detA, gdje je A* pridružena matrica, detA je originalna matrica. Pridružena matrica je transponirana matrica dodataka elementima originalne matrice.

Prije svega, pronađite determinantu matrice, ona mora biti različita od nule, jer će se kasnije determinanta koristiti kao djelitelj. Neka, na primjer, bude data matrica trećeg (sastoji se od tri reda i tri kolone). Kao što vidite, determinanta matrice nije jednaka nuli, tako da postoji inverzna matrica.

Naći komplemente za svaki element matrice A. Komplement za A je determinanta podmatrice dobijena iz originala brisanjem i-tog reda i j-te kolone, a ova determinanta se uzima sa predznakom. Predznak se određuje množenjem determinante sa (-1) na stepen i+j. Tako će, na primjer, komplement A biti determinanta koja se razmatra na slici. Znak je ispao ovako: (-1)^(2+1) = -1.

Kao rezultat ćete dobiti matrica dodatke, sada ga transponujte. Transponiranje je operacija koja je simetrična oko glavne dijagonale matrice; stupci i redovi se zamjenjuju. Dakle, pronašli ste pridruženu matricu A*.

Ova tema je jedna od najomraženijih među studentima. Najgore su, vjerovatno, kvalifikacije.

Trik je u tome što nas sam koncept inverznog elementa (a ne govorim samo o matricama) upućuje na operaciju množenja. Čak iu školskom programu množenje se smatra složenom operacijom, a množenje matrica je generalno posebna tema, kojoj sam posvetio cijeli pasus i video lekciju.

Danas nećemo ulaziti u detalje matričnih proračuna. Prisjetimo se samo: kako se označavaju matrice, kako se množe i šta iz toga slijedi.

Pregled: Množenje matrica

Prije svega, dogovorimo se oko notacije. Matrica $A$ veličine $\left[ m\times n \right]$ je jednostavno tabela brojeva sa tačno $m$ redova i $n$ kolona:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrica) \desno])_(n)\]

Da ne biste slučajno pomiješali redove i kolone (vjerujte, na ispitu možete pobrkati jedan sa dva, a kamoli neke redove), samo pogledajte sliku:

Određivanje indeksa za ćelije matriksa

Šta se dešava? Ako standardni koordinatni sistem $OXY$ postavite u gornji lijevi ugao i usmjerite ose tako da pokrivaju cijelu matricu, onda svaka ćelija ove matrice može biti jedinstveno povezana sa koordinatama $\left(x;y \right)$ - ovo će biti broj reda i kolone.

Zašto je koordinatni sistem postavljen u gornji levi ugao? Da, jer odatle počinjemo čitati bilo kakve tekstove. Vrlo je lako zapamtiti.

Zašto je osa $x$ usmjerena prema dolje, a ne udesno? Opet, jednostavno je: uzmite standardni koordinatni sistem ($x$ osa ide udesno, $y$ osa ide gore) i rotirajte ga tako da pokrije matricu. Ovo je rotacija za 90 stepeni u smeru kazaljke na satu - vidimo rezultat na slici.

Općenito, shvatili smo kako odrediti indekse matričnih elemenata. Pogledajmo sada množenje.

Definicija. Matrice $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$, kada se broj kolona u prvoj poklapa sa brojem redova u drugoj, su naziva konzistentan.

Tačno tim redosledom. Može se zbuniti i reći da matrice $A$ i $B$ čine uređeni par $\left(A;B \right)$: ako su konzistentne u ovom redoslijedu, onda uopće nije potrebno da $B $ i $A$ one. par $\left(B;A \right)$ je takođe konzistentan.

Samo uparene matrice se mogu množiti.

Definicija. Proizvod usklađenih matrica $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$ je nova matrica $C=\left[ m\times k \right ]$ , čiji se elementi $((c)_(ij))$ izračunavaju prema formuli:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Drugim riječima: da biste dobili element $((c)_(ij))$ matrice $C=A\cdot B$, trebate uzeti $i$-red prve matrice, $j$ -ti stupac druge matrice, a zatim pomnožiti u parovima elemente iz ovog reda i kolone. Zbrojite rezultate.

Da, to je tako oštra definicija. Iz toga odmah slijedi nekoliko činjenica:

Množenje matrice, općenito govoreći, nije komutativno: $A\cdot B\ne B\cdot A$;
Međutim, množenje je asocijativno: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
Čak i distributivno: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
I još jednom distributivno: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Distributivnost množenja je morala biti opisana odvojeno za lijevi i desni faktor sume upravo zbog nekomutativnosti operacije množenja.

Ako se ispostavi da je $A\cdot B=B\cdot A$, takve matrice se nazivaju komutativne.

Među svim matricama koje se tamo nečim množe, postoje posebne - one koje, kada se pomnože bilo kojom matricom $A$, opet daju $A$:

Definicija. Matrica $E$ se naziva identitetom ako je $A\cdot E=A$ ili $E\cdot A=A$. U slučaju kvadratne matrice $A$ možemo napisati:

Matrica identiteta je čest gost prilikom rješavanja matričnih jednadžbi. I općenito čest gost u svijetu matrica. :)

I zbog ovog $E$, neko je smislio sve gluposti koje će se dalje pisati.

Šta je inverzna matrica

Budući da je množenje matrice vrlo naporna operacija (morate pomnožiti gomilu redova i stupaca), koncept inverzne matrice također se ispostavlja da nije najtrivijalniji. I zahtijeva neko objašnjenje.

Ključna definicija

Pa, vrijeme je da saznamo istinu.

Definicija. Matrica $B$ se zove inverzna matrici $A$ if

Inverzna matrica je označena sa $((A)^(-1))$ (ne treba je brkati sa stepenom!), tako da se definicija može prepisati na sljedeći način:

Čini se da je sve krajnje jednostavno i jasno. Ali kada analiziramo ovu definiciju, odmah se nameće nekoliko pitanja:

Da li inverzna matrica uvijek postoji? I ako ne uvijek, kako onda odrediti: kada postoji, a kada ne?
A ko je rekao da postoji tačno jedna takva matrica? Šta ako za neku početnu matricu $A$ postoji čitava gomila inverza?
Kako izgledaju svi ovi „preokreti“? I kako, tačno, da ih brojimo?

Što se tiče algoritama proračuna, o tome ćemo govoriti nešto kasnije. Ali na preostala pitanja ćemo odmah odgovoriti. Formulirajmo ih u obliku zasebnih iskaza-lema.

Osnovna svojstva

Počnimo od toga kako bi matrica $A$ u principu trebala izgledati da bi za nju postojao $((A)^(-1))$. Sada ćemo se pobrinuti da obje ove matrice moraju biti kvadratne i iste veličine: $\left[ n\times n \right]$.

Lema 1. Date matricu $A$ i njen inverzni $((A)^(-1))$. Tada su obje ove matrice kvadratne, i istog reda $n$.

Dokaz. To je jednostavno. Neka je matrica $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Budući da proizvod $A\cdot ((A)^(-1))=E$ postoji po definiciji, matrice $A$ i $((A)^(-1))$ su konzistentne u prikazanom redoslijedu:

\[\begin(poravnati) & \left[ m\puta n \desno]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( poravnati)\]

Ovo je direktna posljedica algoritma množenja matrice: koeficijenti $n$ i $a$ su "tranzitni" i moraju biti jednaki.

Istovremeno je definirano i obrnuto množenje: $((A)^(-1))\cdot A=E$, stoga su matrice $((A)^(-1))$ i $A$ također konzistentan u navedenom redoslijedu:

\[\begin(poravnati) & \left[ a\puta b \desno]\cdot \left[ m\times n \right]=\left[ a\puts n \right] \\ & b=m \end( poravnati)\]

Dakle, bez gubitka opštosti, možemo pretpostaviti da je $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Međutim, prema definiciji $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, stoga se veličine matrica striktno podudaraju:

\[\početak(poravnati) & \lijevo[ m\puta n \desno]=\lijevo[ n\puta m \desno] \\ & m=n \end(poravnati)\]

Dakle, ispada da su sve tri matrice - $A$, $(A)^(-1))$ i $E$ - kvadratne matrice veličine $\left[ n\puta n \right]$. Lema je dokazana.

Pa, to je već dobro. Vidimo da su samo kvadratne matrice invertibilne. Sada se uvjerimo da je inverzna matrica uvijek ista.

Lema 2. Date matricu $A$ i njen inverzni $((A)^(-1))$. Tada je ova inverzna matrica jedina.

Dokaz. Idemo kontradiktorno: neka matrica $A$ ima najmanje dva inverza - $B$ i $C$. Tada su, prema definiciji, tačne sljedeće jednakosti:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(poravnati)\]

Iz leme 1 zaključujemo da su sve četiri matrice - $A$, $B$, $C$ i $E$ - kvadrati istog reda: $\left[ n\times n \right]$. Dakle, proizvod je definiran:

Pošto je množenje matrice asocijativno (ali ne i komutativno!), možemo napisati:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \desno)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end(poravnati)\]

Dobili smo jedinu moguću opciju: dvije kopije inverzne matrice su jednake. Lema je dokazana.

Gornji argumenti ponavljaju gotovo doslovno dokaz jedinstvenosti inverznog elementa za sve realne brojeve $b\ne 0$. Jedini značajan dodatak je uzimanje u obzir dimenzije matrica.

Međutim, još uvijek ne znamo ništa o tome da li je svaka kvadratna matrica inverzibilna. Ovdje nam u pomoć priskače determinanta - ovo je ključna karakteristika za sve kvadratne matrice.

Lema 3. Zadana je matrica $A$. Ako postoji njena inverzna matrica $((A)^(-1))$, tada je determinanta originalne matrice različita od nula:

\[\lijevo| A\desno|\ne 0\]

Dokaz. Već znamo da su $A$ i $((A)^(-1))$ kvadratne matrice veličine $\left[ n\puta n \right]$. Dakle, za svaki od njih možemo izračunati determinantu: $\left| A\desno|$ i $\levo| ((A)^(-1)) \right|$. Međutim, determinanta proizvoda jednaka je proizvodu determinanti:

\[\lijevo| A\cdot B \desno|=\lijevo| A \desno|\cdot \levo| B \right|\Rightarrow \levo| A\cdot ((A)^(-1)) \desno|=\lijevo| A \desno|\cdot \levo| ((A)^(-1)) \desno|\]

Ali prema definiciji, $A\cdot ((A)^(-1))=E$, a determinanta $E$ je uvijek jednaka 1, tako da

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \lijevo| A\cdot ((A)^(-1)) \desno|=\lijevo| E\desno|; \\ & \lijevo| A \desno|\cdot \levo| ((A)^(-1)) \right|=1. \\ \end(poravnati)\]

Proizvod dva broja jednak je jedan samo ako je svaki od ovih brojeva različit od nule:

\[\lijevo| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Dakle, ispada da je $\left| A \right|\ne 0$. Lema je dokazana.

Zapravo, ovaj zahtjev je sasvim logičan. Sada ćemo analizirati algoritam za pronalaženje inverzne matrice - i biće potpuno jasno zašto, sa nultom determinantom, inverzna matrica u principu ne može postojati.

Ali prvo, formulirajmo "pomoćnu" definiciju:

Definicija. Singularna matrica je kvadratna matrica veličine $\left[ n\puta n \right]$ čija je determinanta nula.

Dakle, možemo tvrditi da je svaka invertibilna matrica nesingularna.

Kako pronaći inverz od matrice

Sada ćemo razmotriti univerzalni algoritam za pronalaženje inverznih matrica. Generalno, postoje dva općeprihvaćena algoritma, a danas ćemo razmotriti i drugi.

Ona o kojoj ćemo sada govoriti je vrlo efikasna za matrice veličine $\left[ 2\times 2 \right]$ i - djelimično - veličine $\left[ 3\times 3 \right]$. Ali počevši od veličine $\left[ 4\times 4 \right]$ bolje je ne koristiti je. Zašto - sada ćete sve sami shvatiti.

Algebarski dodaci

Spremiti se. Sada će biti bola. Ne, ne brini: lijepa medicinska sestra u suknji, čarapama sa čipkom neće ti doći i dati ti injekciju u zadnjicu. Sve je mnogo prozaičnije: algebarski dodaci i Njeno Veličanstvo "Matrica Unije" dolaze vam.

Počnimo od glavne stvari. Neka postoji kvadratna matrica veličine $A=\left[ n\times n \right]$, čiji se elementi nazivaju $((a)_(ij))$. Tada za svaki takav element možemo definirati algebarski komplement:

Definicija. Algebarski komplement $((A)_(ij))$ elementu $((a)_(ij))$ koji se nalazi u $i$th redu i $j$toj koloni matrice $A=\left[ n \times n \right]$ je konstrukcija forme

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Gdje je $M_(ij)^(*)$ determinanta matrice dobijene iz originalnog $A$ brisanjem istog $i$th reda i $j$th kolone.

Opet. Algebarski komplement matričnom elementu sa koordinatama $\left(i;j \right)$ označava se kao $((A)_(ij))$ i izračunava se prema šemi:

Prvo, brišemo $i$-red i $j$-tu kolonu iz originalne matrice. Dobijamo novu kvadratnu matricu i njenu determinantu označavamo sa $M_(ij)^(*)$.
Zatim pomnožimo ovu determinantu sa $((\left(-1 \right))^(i+j))$ - u početku ovaj izraz može izgledati zapanjujuće, ali u suštini jednostavno otkrivamo znak ispred $M_(ij)^(*) $.
Računamo i dobijamo konkretan broj. One. algebarsko sabiranje je upravo broj, a ne neka nova matrica itd.

Sama matrica $M_(ij)^(*)$ naziva se dodatnim minorom elementu $((a)_(ij))$. I u tom smislu, gornja definicija algebarskog komplementa je poseban slučaj složenije definicije – onoga što smo gledali u lekciji o determinanti.

Važna napomena. Zapravo, u matematici „odraslih“ algebarski sabirci se definiraju na sljedeći način:

Uzimamo $k$ redova i $k$ kolona u kvadratnoj matrici. Na njihovom preseku dobijamo matricu veličine $\left[ k\times k \right]$ - njena determinanta se naziva minor reda $k$ i označava se kao $((M)_(k))$.

Zatim precrtavamo ove “odabrane” $k$ redove i $k$ kolone. Još jednom dobijate kvadratnu matricu - njena determinanta se zove dodatni minor i označava se kao $M_(k)^(*)$.

Pomnožite $M_(k)^(*)$ sa $((\left(-1 \right))^(t))$, gdje je $t$ (pažnja!) zbir brojeva svih odabranih redova i kolone. Ovo će biti algebarski dodatak.

Pogledajte treći korak: zapravo postoji zbir termina od $2k$! Druga stvar je što ćemo za $k=1$ dobiti samo 2 člana - to će biti isti $i+j$ - "koordinate" elementa $((a)_(ij))$ za koji smo tražeći algebarski komplement.

Dakle, danas koristimo malo pojednostavljenu definiciju. Ali kako ćemo kasnije vidjeti, to će biti više nego dovoljno. Mnogo je važnija sledeća stvar:

Definicija. Povezana matrica $S$ sa kvadratnom matricom $A=\left[ n\times n \right]$ je nova matrica veličine $\left[ n\times n \right]$, koja se dobija iz $A$ zamjenom $(( a)_(ij))$ algebarskim dodacima $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrica) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrica) \desno]\]

Prva pomisao koja se nameće u trenutku realizacije ove definicije je “koliko će se morati izbrojati!” Opustite se: moraćete da računate, ali ne toliko. :)

Pa, sve je ovo jako lepo, ali zašto je potrebno? Ali zašto.

Glavna teorema

Vratimo se malo unazad. Zapamtite, u lemi 3 je navedeno da je invertibilna matrica $A$ uvijek nesingularna (to jest, njena determinanta nije nula: $\left| A \right|\ne 0$).

Dakle, istina je i suprotno: ako matrica $A$ nije singularna, onda je uvijek inverzibilna. Čak postoji i šema pretraživanja za $((A)^(-1))$. Provjeri:

Teorema inverzne matrice. Neka je data kvadratna matrica $A=\left[ n\times n \right]$, a njena determinanta je različita od nule: $\left| A \right|\ne 0$. Tada inverzna matrica $((A)^(-1))$ postoji i izračunava se po formuli:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

A sada - sve je isto, ali čitljivim rukopisom. Da biste pronašli inverznu matricu, trebate:

Izračunajte determinantu $\left| \right|$ i uvjerite se da nije nula.
Konstruirajte union matricu $S$, tj. izbrojte 100500 algebarskih dodataka $((A)_(ij))$ i postavite ih na mjesto $((a)_(ij))$.
Transponirajte ovu matricu $S$, a zatim je pomnožite nekim brojem $q=(1)/(\left| A \right|)\;$.

To je sve! Inverzna matrica $((A)^(-1))$ je pronađena. Pogledajmo primjere:

\[\left[ \begin(matrica) 3 & 1 \\ 5 & 2 \\\end(matrica) \right]\]

Rješenje. Hajde da proverimo reverzibilnost. Izračunajmo determinantu:

\[\lijevo| A\desno|=\lijevo| \begin(matrica) 3 & 1 \\ 5 & 2 \\\end(matrica) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Odrednica se razlikuje od nule. To znači da je matrica invertibilna. Kreirajmo matricu sindikata:

Izračunajmo algebarske sabirke:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2 \right|=2; \\ & ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| 5 \right|=-5; \\ & ((A)_(21))=((\lijevo(-1 \desno))^(2+1))\cdot \lijevo| 1 \right|=-1; \\ & ((A)_(22))=((\lijevo(-1 \desno))^(2+2))\cdot \lijevo| 3\desno|=3. \\ \end(poravnati)\]

Obratite pažnju: determinante |2|, |5|, |1| i |3| su determinante matrica veličine $\left[ 1\puts 1 \right]$, a ne moduli. One. Ako su u determinantama bili negativni brojevi, nema potrebe za uklanjanjem “minusa”.

Ukupno, naša sindikalna matrica izgleda ovako:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(niz)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(niz) \desno])^(T))=\left[ \begin (niz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(niz) \desno]\]

OK, sve je gotovo. Problem je riješen.

Odgovori. $\left[ \begin(niz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(niz) \right]$

Zadatak. Pronađite inverznu matricu:

\[\left[ \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \desno] \]

Rješenje. Ponovo izračunavamo determinantu:

\[\početi(poravnati) & \lijevo| \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \right|=\begin(matrica ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrica)= \ \ & =\left(2+1+0 \desno)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Determinanta je različita od nule - matrica je invertibilna. Ali sada će biti jako teško: trebamo izbrojati čak 9 (devet, jebem ti mater!) algebarskih dodataka. I svaki od njih će sadržavati determinantu $\left[ 2\puts 2 \right]$. leteo:

\[\begin(matrica) ((A)_(11))=((\left(-1 \desno))^(1+1))\cdot \left| \begin(matrica) 2 & -1 \\ 0 & 1 \\\end(matrica) \right|=2; \\ ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \\ ((A)_(13))=((\lijevo(-1 \desno))^(1+3))\cdot \lijevo| \begin(matrica) 0 & 2 \\ 1 & 0 \\\end(matrica) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \desno))^(3+3))\cdot \left| \begin(matrica) 1 & -1 \\ 0 & 2 \\\end(matrica) \right|=2; \\ \end(matrica)\]

Ukratko, matrica sindikata će izgledati ovako:

Dakle, inverzna matrica će biti:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrica) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrica) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \2 & 1 & -2 \\\kraj (niz) \desno]\]

To je to. Evo odgovora.

Odgovori. $\left[ \begin(niz)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(niz) \right ]$

Kao što vidite, na kraju svakog primjera izvršili smo provjeru. S tim u vezi, važna napomena:

Ne budite lijeni provjeriti. Pomnožite originalnu matricu sa pronađenom inverznom matricom - trebali biste dobiti $E$.

Izvođenje ove provjere je mnogo lakše i brže od traženja greške u daljim proračunima kada, na primjer, rješavate matričnu jednačinu.

Alternativni način

Kao što sam rekao, teorema inverzne matrice odlično radi za veličine $\left[ 2\times 2 \right]$ i $\left[ 3\times 3 \right]$ (u drugom slučaju, nije tako "odlično" " ), ali za veće matrice počinje tuga.

Ali ne brinite: postoji alternativni algoritam s kojim možete mirno pronaći inverz čak i za matricu $\left[ 10\x 10 \right]$. Ali, kao što se često dešava, da bismo razmotrili ovaj algoritam potrebno nam je malo teorijskog uvoda.

Elementarne transformacije

Među svim mogućim matričnim transformacijama postoji nekoliko posebnih - nazivaju se elementarnim. Postoje tačno tri takve transformacije:

Množenje. Možete uzeti $i$-ti red (kolona) i pomnožiti ga bilo kojim brojem $k\ne 0$;
Dodatak. Dodajte u $i$-ti red (kolona) bilo koji drugi $j$-ti red (kolona), pomnožen sa bilo kojim brojem $k\ne 0$ (možete, naravno, učiniti $k=0$, ali šta je poenta? ? Ništa se neće promijeniti).
Preuređenje. Uzmite $i$th i $j$th redove (kolone) i zamijenite mjesta.

Zašto se ove transformacije nazivaju elementarnim (za velike matrice ne izgledaju tako elementarne) i zašto ih ima samo tri - ova pitanja su izvan okvira današnje lekcije. Stoga, nećemo ulaziti u detalje.

Još jedna stvar je važna: sve ove perverzije moramo izvesti na adjuint matrici. Da, da: dobro ste čuli. Sada će biti još jedna definicija - posljednja u današnjoj lekciji.

Adjoint matrica

Sigurno ste u školi rješavali sisteme jednačina metodom sabiranja. Pa, eto, oduzmite drugu od jedne linije, pomnožite neki red brojem - to je sve.

Dakle: sada će sve biti isto, ali na „odrasli“ način. Spreman?

Definicija. Neka su data matrica $A=\left[ n\times n \right]$ i matrica identiteta $E$ iste veličine $n$. Tada je pridružena matrica $\left[ A\left| E\desno. \right]$ je nova matrica veličine $\left[ n\puta 2n \right]$ koja izgleda ovako:

\[\lijevo[ A\lijevo| E\desno. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & (a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(niz) \desno]\]

Ukratko, uzimamo matricu $A$, desno joj dodjeljujemo matricu identiteta $E$ tražene veličine, odvajamo ih vertikalnom trakom radi ljepote - evo vam adjoint. :)

u čemu je kvaka? Evo šta:

Teorema. Neka je matrica $A$ invertibilna. Razmotrimo pridruženu matricu $\left[ A\left| E\desno. \right]$. Ako koristite elementarne konverzije nizova dovedite ga u oblik $\left[ E\left| Svijetao. \right]$, tj. množenjem, oduzimanjem i preuređivanjem redova da se od $A$ dobije matrica $E$ s desne strane, tada je matrica $B$ dobijena s lijeve strane inverzna od $A$:

\[\lijevo[ A\lijevo| E\desno. \desno]\na \lijevo[ E\lijevo| Svijetao. \right]\Rightarrow B=((A)^(-1))\]

To je tako jednostavno! Ukratko, algoritam za pronalaženje inverzne matrice izgleda ovako:

Napišite pridruženu matricu $\left[ A\left| E\desno. \right]$;
Izvodite elementarne konverzije nizova dok se ne pojavi $E$ umjesto $A$;
Naravno, nešto će se pojaviti i na lijevoj strani - određena matrica $B$. Ovo će biti suprotno;
PROFIT!:)

Naravno, ovo je mnogo lakše reći nego učiniti. Dakle, pogledajmo nekoliko primjera: za veličine $\left[ 3\times 3 \right]$ i $\left[ 4\times 4 \right]$.

Zadatak. Pronađite inverznu matricu:

\[\left[ \begin(niz)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(niz) \desno]\ ]

Rješenje. Kreiramo pridruženu matricu:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\kraj (niz) \desno]\]

Budući da je posljednja kolona originalne matrice popunjena jedinicama, oduzmite prvi red od ostatka:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\kraj(niz) \desno]\početak(matrica) \strelica prema dolje \\ -1 \\ -1 \\\kraj(matrica)\do \\ & \na \lijevo [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(niz) \desno] \\ \end(poravnati)\]

Nema više jedinica, osim prve linije. Ali mi to ne diramo, inače će se novouklonjene jedinice početi "množavati" u trećem stupcu.

Ali možemo dva puta oduzeti drugi red od posljednjeg - dobijamo jedan u donjem lijevom uglu:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\kraj(niz) \desno]\početak(matrica) \ \\ \strelica prema dolje \\ -2 \\\kraj(matrica)\do \\ & \lijevo [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno] \\ \end(poravnati)\]

Sada možemo oduzeti posljednji red od prvog i dva puta od drugog - na ovaj način "nuliramo" prvi stupac:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno]\početak(matrica) -1 \\ -2 \\ \uparrow \\\end(matrica)\do \\ & \ na \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj (niz) \desno] \\ \end(poravnanje)\]

Pomnožite drugi red sa −1, a zatim ga oduzmite 6 puta od prvog i dodajte 1 put poslednjem:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj(niz) \desno]\početak(matrica) \ \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \ \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj(niz) \desno]\početak(matrica) -6 \\ \strelica nagore \\ +1 \\\end (matrica)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\kraj (niz) \desno] \\ \end(poravnanje)\]

Ostaje samo zamijeniti redove 1 i 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\kraj (niz) \desno]\]

Spremni! Desno je tražena inverzna matrica.

Odgovori. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Zadatak. Pronađite inverznu matricu:

\[\left[ \begin(matrica) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\kraj (matrica) \desno]\]

Rješenje. Ponovo sastavljamo adjoint:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\kraj (niz) \desno]\]

Hajde da se malo rasplačemo, da budemo tužni koliko sada moramo da brojimo... i počnimo da brojimo. Prvo, hajde da "nulimo" prvu kolonu oduzimanjem reda 1 od reda 2 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(niz) \desno]\begin(matrica) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(niz) \desno] \\ \end(align)\]

Vidimo previše "protiv" u redovima 2-4. Pomnožite sva tri reda sa −1, a zatim spalite treći stupac oduzimanjem reda 3 od ostatka:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(niz) \desno]\početak(matrica) \ \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (niz) \desno]\početak(matrica) -2 \\ -1 \\ \strelica nagore \\ -2 \\\kraj(matrica)\na \\ & \na \levo[ \begin(niz)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno] \\ \end(align)\]

Sada je vrijeme da se "prži" posljednji stupac originalne matrice: od ostatka oduzmite red 4:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz ) \desno]\begin(matrica) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\kraj (niz) \desno] \\ \end(poravnanje)\]

Završno bacanje: "sagorite" drugu kolonu oduzimanjem reda 2 od redova 1 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( niz) \desno]\početak(matrica) 6 \\ \strelica nagore \\ -5 \\ \ \\\end(matrica)\to \\ & \to \left[ \begin(niz)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno] \\ \end(align)\]

I opet je matrica identiteta na lijevoj strani, što znači da je inverzna desno. :)

Odgovori. $\left[ \begin(matrica) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrica) \desno]$

OK, sve je gotovo. Provjeri sam - sjeban sam. :)

ALGEBARSKI KOMPLEMENTI I MINORI

Neka nam je determinanta trećeg reda: .

Minor, koji odgovara ovom elementu a ij determinanta trećeg reda naziva se determinanta drugog reda dobijena iz date brisanjem reda i kolone na čijem presjeku se nalazi dati element, tj. i-ti red i j th column. Maloljetnici koji odgovaraju datom elementu a ij označićemo M ij.

Na primjer, minor M 12, koji odgovara elementu a 12, postojaće odrednica 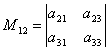, koji se dobija brisanjem 1. reda i 2. kolone iz ove determinante.

Dakle, formula koja definira determinantu trećeg reda pokazuje da je ta determinanta jednaka zbroju proizvoda elemenata 1. reda po njihovim odgovarajućim minorima; u ovom slučaju minor koji odgovara elementu a 12, uzima se sa znakom “–”, tj. možemo to napisati

(1)

Slično, mogu se uvesti definicije minora za determinante drugog i višeg reda.

Hajde da predstavimo još jedan koncept.

Algebarski komplement element a ij determinanta se zove njen minor M ij, pomnoženo sa (–1) i+j .

Algebarski komplement elementa a ij označeno sa A ij.

Iz definicije dobijamo da se veza između algebarskog komplementa elementa i njegovog minora izražava jednakošću A ij= (–1) i+j Mij.

Na primjer,

Primjer. Zadana je determinanta. Nađi A 13, A 21, A 32.

Lako je vidjeti da se pomoću algebarskih sabiranja elemenata formula (1) može napisati kao:

Slično ovoj formuli, možete dobiti proširenje determinante u elemente bilo kojeg reda ili stupca.

Na primjer, dekompozicija determinante na elemente 2. reda može se dobiti na sljedeći način. Prema svojstvu 2 determinante imamo:

Proširimo rezultujuću determinantu na elemente 1. reda.

(2)

Odavde jer determinante drugog reda u formuli (2) su minori elemenata a 21, a 22, a 23. Dakle, tj. dobili smo dekompoziciju determinante na elemente 2. reda.

Slično, možemo dobiti proširenje determinante u elemente trećeg reda. Koristeći svojstvo 1 determinanti (o transpoziciji), možemo pokazati da slična proširenja vrijede i kada se širimo preko elemenata stupaca.

Dakle, vrijedi sljedeća teorema.

Teorema (o proširenju determinante preko datog reda ili stupca). Determinanta je jednaka zbroju proizvoda elemenata bilo kojeg njegovog reda (ili stupca) i njihovih algebarskih komplementa.

Sve gore navedeno vrijedi i za determinante bilo kojeg višeg reda.

Primjeri.

INVERZNA MATRICA

Koncept inverzne matrice se uvodi samo za kvadratne matrice.

Ako A je kvadratna matrica, dakle obrnuto za to je matrica matrica, označena A-1 i zadovoljavanjem uslova. (Ova definicija je uvedena po analogiji sa množenjem brojeva)

Matrica $A^(-1)$ se naziva inverznom kvadratne matrice $A$ ako je ispunjen uslov $A^(-1)\cdot A=A\cdot A^(-1)=E$, gdje je $E $ matrica identiteta, čiji je red jednak redu matrice $A$.

Nesingularna matrica je matrica čija determinanta nije jednaka nuli. Prema tome, singularna matrica je ona čija je determinanta jednaka nuli.

Inverzna matrica $A^(-1)$ postoji ako i samo ako je matrica $A$ nesingularna. Ako inverzna matrica $A^(-1)$ postoji, onda je jedinstvena.

Postoji nekoliko načina za pronalaženje inverza matrice, a mi ćemo pogledati dva od njih. Ova stranica će raspravljati o metodi spojene matrice, koja se smatra standardnom u većini viših matematičkih kurseva. Druga metoda pronalaženja inverzne matrice (metoda elementarnih transformacija), koja uključuje korištenje Gaussove metode ili Gauss-Jordanove metode, razmatra se u drugom dijelu.

Metoda spojene matrice

Neka je data matrica $A_(n\puta n)$. Da bi se pronašla inverzna matrica $A^(-1)$, potrebna su tri koraka:

Pronađite determinantu matrice $A$ i uvjerite se da je $\Delta A\neq 0$, tj. da je matrica A nesingularna.
Sastavite algebarske komplemente $A_(ij)$ svakog elementa matrice $A$ i napišite matricu $A_(n\puta n)^(*)=\left(A_(ij) \right)$ iz pronađene algebarske dopunjuje.
Napišite inverznu matricu uzimajući u obzir formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Matrica $(A^(*))^T$ se često naziva adjunktnom (recipročnom, povezanom) sa matricom $A$.

Ako se rješenje radi ručno, onda je prva metoda dobra samo za matrice relativno malog reda: drugi (), treći (), četvrti (). Za pronalaženje inverza matrice višeg reda koriste se druge metode. Na primjer, Gaussova metoda, o kojoj se govori u drugom dijelu.

Primjer br. 1

Pronađite inverznu vrijednost matrice $A=\left(\begin(niz) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(niz) \desno)$.

Pošto su svi elementi četvrtog stupca jednaki nuli, onda je $\Delta A=0$ (tj. matrica $A$ je singularna). Pošto je $\Delta A=0$, ne postoji inverzna matrica prema matrici $A$.

Odgovori: matrica $A^(-1)$ ne postoji.

Primjer br. 2

Pronađite inverz matrice $A=\left(\begin(niz) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Izvršite provjeru.

Koristimo metodu spojene matrice. Prvo, pronađimo determinantu date matrice $A$:

$$ \Delta A=\lijevo| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Pošto je $\Delta A \neq 0$, onda postoji inverzna matrica, stoga ćemo nastaviti sa rješenjem. Pronalaženje algebarskih komplementa

\begin(poravnano) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(poravnano)

Sastavljamo matricu algebarskih sabiranja: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transponiramo rezultirajuću matricu: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ ( rezultirajuća matrica se često naziva pridruženom ili povezanom matricom sa matricom $A$). Koristeći formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, imamo:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(niz) (cc) 8 & -7\\ -9 & -5 \end(niz)\desno) =\left(\begin(niz) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(niz)\desno) $$

Dakle, pronađena je inverzna matrica: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array )\desno) $. Da biste provjerili istinitost rezultata, dovoljno je provjeriti istinitost jedne od jednakosti: $A^(-1)\cdot A=E$ ili $A\cdot A^(-1)=E$. Provjerimo jednakost $A^(-1)\cdot A=E$. Da bismo manje radili sa razlomcima, zamijenit ćemo matricu $A^(-1)$ ne u obliku $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$, iu obliku $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(niz)\desno)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( niz)\desno)\cdot\left(\begin(niz) (cc) -5 & 7 \\ 9 & 8 \end(niz)\desno) =-\frac(1)(103)\cdot\left( \begin(niz) (cc) -103 & 0 \\ 0 & -103 \end(niz)\desno) =\left(\begin(niz) (cc) 1 & 0 \\ 0 & 1 \end(niz )\desno) =E $$

Odgovori: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Primjer br. 3

Pronađite inverznu matricu za matricu $A=\left(\begin(niz) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(niz) \right)$ . Izvršite provjeru.

Počnimo s izračunavanjem determinante matrice $A$. Dakle, determinanta matrice $A$ je:

$$ \Delta A=\lijevo| \begin(niz) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(niz) \right| = 18-36+56-12=26. $$

Pošto je $\Delta A\neq 0$, tada postoji inverzna matrica, stoga ćemo nastaviti sa rješenjem. Pronalazimo algebarske komplemente svakog elementa date matrice:

Sastavljamo matricu algebarskih sabiranja i transponiramo je:

$$ A^*=\left(\begin(niz) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(niz) \desno); \; (A^*)^T=\left(\begin(niz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(niz) \desno) . $$

Koristeći formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, dobijamo:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(niz) \desno)= \lijevo(\begin(niz) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(niz) \desno) $$

Dakle $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(niz) \desno)$. Da biste provjerili istinitost rezultata, dovoljno je provjeriti istinitost jedne od jednakosti: $A^(-1)\cdot A=E$ ili $A\cdot A^(-1)=E$. Provjerimo jednakost $A\cdot A^(-1)=E$. Da bismo manje radili sa razlomcima, zamijenit ćemo matricu $A^(-1)$ ne u obliku $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, iu obliku $\frac(1)(26 )\cdot \left( \begin(niz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(niz) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(niz)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(niz) \desno)\cdot \frac(1)(26)\cdot \left(\begin(niz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ kraj(niz) \desno) =\frac(1)(26)\cdot\left(\begin(niz) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (niz) \desno) =\left(\begin(niz) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(niz) \right) =E $$

Provjera je bila uspješna, inverzna matrica $A^(-1)$ je ispravno pronađena.

Odgovori: $A^(-1)=\left(\begin(niz) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(niz) \desno)$.

Primjer br. 4

Pronađite matricu inverznu matrici $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(niz) \desno)$.

Za matricu četvrtog reda, pronalaženje inverzne matrice pomoću algebarskih sabiranja je donekle teško. Međutim, takvi primjeri se javljaju u testnim radovima.

Da biste pronašli inverznu vrijednost matrice, prvo morate izračunati determinantu matrice $A$. Najbolji način da to učinite u ovoj situaciji je dekomponiranje determinante duž reda (kolone). Odabiremo bilo koji red ili stupac i pronalazimo algebarske komplemente svakog elementa odabranog reda ili stupca.

Na primjer, za prvi red dobijamo:

$$ A_(11)=\left|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(niz)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\left|\begin(niz)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(niz)\right|= -536;\; A_(14)=-\left|\begin(niz)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(niz)\right|=-112. $$

Determinanta matrice $A$ se izračunava pomoću sljedeće formule:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14 )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(poravnano) $$

Matrica algebarskih komplemenata: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36\\ 473 & -250 & -463 & -96\end(array)\right)$.

Adjoint matrica: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Inverzna matrica:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Provjera se, po želji, može izvršiti na isti način kao u prethodnim primjerima.

Odgovori: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(niz) \desno) $.

U drugom dijelu ćemo razmotriti još jedan način pronalaženja inverzne matrice, koji uključuje korištenje transformacija Gaussove metode ili Gauss-Jordan metode.

Neka nam je data kvadratna matrica. Morate pronaći inverznu matricu.

Prvi način. Teorema 4.1 o postojanju i jedinstvenosti inverzne matrice ukazuje na jedan od načina da se ona pronađe.

1. Izračunajte determinantu ove matrice. Ako, onda inverzna matrica ne postoji (matrica je singularna).

2. Konstruisati matricu od algebarskih komplemenata matričnih elemenata.

3. Transponirajte matricu da dobijete pridruženu matricu .

4. Pronađite inverznu matricu (4.1) dijeljenjem svih elemenata spojene matrice determinantom

Drugi način. Da biste pronašli inverznu matricu, možete koristiti elementarne transformacije.

1. Konstruirajte blok matricu dodjeljivanjem datoj matrici matricu identiteta istog reda.

2. Koristeći elementarne transformacije izvršene na redovima matrice, dovedite njen lijevi blok u najjednostavniji oblik. U ovom slučaju, blok matrica se svodi na oblik gdje je kvadratna matrica dobivena kao rezultat transformacija iz matrice identiteta.

3. Ako je , tada je blok jednak inverzu matrice, tj. Ako, onda matrica nema inverz.

Zapravo, uz pomoć elementarnih transformacija redova matrice, moguće je njen lijevi blok svesti na pojednostavljeni oblik (vidi sliku 1.5). U ovom slučaju, blok matrica se transformira u oblik gdje je elementarna matrica koja zadovoljava jednakost. Ako je matrica nedegenerirana, tada se prema stavu 2. Napomene 3.3 njen pojednostavljeni oblik poklapa s matricom identiteta. Tada iz jednakosti slijedi da. Ako je matrica singularna, tada se njen pojednostavljeni oblik razlikuje od matrice identiteta, a matrica nema inverz.

11. Matrične jednadžbe i njihovo rješenje. Matrični oblik snimanja SLAE. Matrična metoda (metoda inverzne matrice) za rješavanje SLAE-a i uvjeti njene primjenjivosti.

Matrične jednačine su jednačine oblika: A*X=C; X*A=C; A*X*B=C gdje su matrice A, B, C poznate, matrica X nepoznata, ako matrice A i B nisu degenerisane, tada će rješenja originalnih matrica biti zapisana u odgovarajućem obliku: X = A -1 * C; X=C*A -1; X=A -1 *C*B -1 Matrični oblik pisanja sistema linearnih algebarskih jednačina. Nekoliko matrica može biti povezano sa svakim SLAE; Štaviše, sam SLAE se može napisati u obliku matrične jednačine. Za SLAE (1), razmotrite sljedeće matrice:

Matrica A se zove matrica sistema. Elementi ove matrice predstavljaju koeficijente date SLAE.

Matrica A˜ se zove prošireni matrični sistem. Dobiva se dodavanjem u matricu sistema kolone koja sadrži slobodne termine b1,b2,...,bm. Obično je ova kolona odvojena okomitom linijom radi jasnoće.

Poziva se matrica stupca B matrica slobodnih članova, a matrica stupaca X je matrica nepoznatih.

Koristeći prethodno uvedenu notaciju, SLAE (1) se može napisati u obliku matrične jednačine: A⋅X=B.

Bilješka

Matrice povezane sa sistemom mogu se pisati na različite načine: sve zavisi od redosleda varijabli i jednačina SLAE koji se razmatra. Ali u svakom slučaju, redoslijed nepoznanica u svakoj jednadžbi date SLAE mora biti isti.

Matrična metoda je pogodna za rješavanje SLAE u kojima se broj jednačina poklapa sa brojem nepoznatih varijabli i determinanta glavne matrice sistema je različita od nule. Ako sistem sadrži više od tri jednačine, tada pronalaženje inverzne matrice zahtijeva značajan računski napor, stoga je u ovom slučaju preporučljivo koristiti Gaussova metoda.

12. Homogene SLAE, uslovi postojanja njihovih nenultih rješenja. Svojstva parcijalnih rješenja homogenih SLAE.

Linearna jednačina se naziva homogenom ako je njen slobodni član jednak nuli, a inače nehomogena. Sistem koji se sastoji od homogenih jednačina naziva se homogenim i ima opšti oblik:

13 .Koncept linearne nezavisnosti i zavisnosti parcijalnih rješenja homogene SLAE. Fundamentalni sistem rješenja (FSD) i njegovo određivanje. Predstavljanje općeg rješenja homogene SLAE kroz FSR.

Funkcijski sistem y 1 (x ), y 2 (x ), …, y n (x ) se zove linearno zavisna na intervalu ( a , b ), ako postoji skup konstantnih koeficijenata koji nisu jednaki nuli u isto vrijeme, tako da je linearna kombinacija ovih funkcija identično jednaka nuli na ( a , b ): Za . Ako je jednakost za moguća samo za , Sistem funkcija y 1 (x ), y 2 (x ), …, y n (x ) se zove linearno nezavisna na intervalu ( a , b ). Drugim riječima, funkcije y 1 (x ), y 2 (x ), …, y n (x ) linearno zavisna na intervalu ( a , b ), ako postoji jednaka nuli na ( a , b ) njihova netrivijalna linearna kombinacija. Funkcije y 1 (x ),y 2 (x ), …, y n (x ) linearno nezavisna na intervalu ( a , b ), ako je samo njihova trivijalna linearna kombinacija identično jednaka nuli na ( a , b ).

Sistem fundamentalnih odluka (FSR) Homogeni SLAE je osnova ovog sistema kolona.

Broj elemenata u FSR-u jednak je broju nepoznatih sistema minus rang sistemske matrice. Svako rješenje originalnog sistema je linearna kombinacija rješenja FSR-a.

Teorema

Opće rješenje nehomogenog SLAE jednako je zbiru određenog rješenja nehomogenog SLAE i opšteg rješenja odgovarajućeg homogenog SLAE.

1 . Ako su kolone rješenja homogenog sistema jednačina, onda je svaka njihova linearna kombinacija također rješenje homogenog sistema.

Zaista, iz jednakosti to slijedi

one. linearna kombinacija rješenja je rješenje za homogeni sistem.

2. Ako je rang matrice homogenog sistema jednak , tada sistem ima linearno nezavisna rješenja.

Zaista, koristeći formule (5.13) za opšte rješenje homogenog sistema, nalazimo pojedina rješenja, dajući slobodnim varijablama sljedeće standardne skupove vrijednosti (svaki put pod pretpostavkom da je jedna od slobodnih varijabli jednaka jedan, a ostale jednake nuli):

koje su linearno nezavisne. U stvari, ako kreirate matricu iz ovih kolona, tada njeni posljednji redovi formiraju matricu identiteta. Prema tome, minor koji se nalazi u zadnjim redovima nije jednak nuli (jednak je jedan), tj. je osnovno. Stoga će rang matrice biti jednak. To znači da su svi stupci ove matrice linearno nezavisni (vidjeti teoremu 3.4).

Bilo koja zbirka linearno nezavisnih rješenja homogenog sistema naziva se osnovni sistem (skup) rješenja .

14 Minor th reda, osnovni mol, rang matrice. Izračunavanje ranga matrice.

Red k minor matrice A je determinanta neke njene kvadratne podmatrice reda k.

U matrici A dimenzija m x n, minor reda r naziva se osnovnim ako je različit od nule, a svi minori višeg reda, ako postoje, jednaki su nuli.

Stupci i redovi matrice A, na čijem se presjeku nalazi bazni minor, nazivaju se osnovni stupci i redovi matrice A.

Teorema 1. (O rangu matrice). Za bilo koju matricu, manji rang je jednak rangu reda i jednak rangu stupca.

Teorema 2. (O baznom molu). Svaki stupac matrice se razlaže u linearnu kombinaciju svojih osnovnih stupaca.

Rang matrice (ili manji rang) je red baznog minora ili, drugim riječima, najveći red za koji postoje minori različiti od nule. Rang nulte matrice se po definiciji smatra 0.

Zapazimo dva očigledna svojstva minornog ranga.

1) Rang matrice se ne menja tokom transpozicije, jer kada se matrica transponuje, sve njene podmatrice se transponuju i minori se ne menjaju.

2) Ako je A’ podmatrica matrice A, onda rang A’ ne prelazi rang A, pošto je manji minor različit od nule uključen u A’ takođe uključen u A.

15. Koncept -dimenzionalnog aritmetičkog vektora. Jednakost vektora. Operacije nad vektorima (sabiranje, oduzimanje, množenje brojem, množenje matricom). Linearna kombinacija vektora.

Naručena kolekcija n nazivaju se realni ili kompleksni brojevi n-dimenzionalni vektor. Zovu se brojevi vektorske koordinate.

Dva (ne-nula) vektora a I b jednaki su ako su jednako usmjereni i imaju isti modul. Svi nulti vektori se smatraju jednakim. U svim ostalim slučajevima vektori nisu jednaki.

Vektorsko dodavanje. Postoje dva načina za dodavanje vektora: 1. Pravilo paralelograma. Da bismo dodali vektore i, stavljamo početak oba u istu tačku. Gradimo do paralelograma i iz iste tačke crtamo dijagonalu paralelograma. Ovo će biti zbir vektora.

2. Drugi metod sabiranja vektora je pravilo trougla. Uzmimo iste vektore i . Dodaćemo početak drugog na kraj prvog vektora. Sada spojimo početak prvog i kraj drugog. Ovo je zbroj vektora i . Koristeći isto pravilo, možete dodati nekoliko vektora. Slažemo ih jedan za drugim, a zatim povezujemo početak prvog s krajem posljednjeg.

Oduzimanje vektora. Vektor je usmjeren suprotno od vektora. Dužine vektora su jednake. Sada je jasno šta je vektorsko oduzimanje. Vektorska razlika i je zbir vektora i vektora .

Množenje vektora brojem

Množenjem vektora brojem k dobija se vektor čija je dužina k puta dužina. Kosmjeran je s vektorom ako je k veći od nule, a suprotno usmjeren ako je k manji od nule.

Skalarni proizvod vektora je proizvod dužina vektora i kosinusa ugla između njih. Ako su vektori okomiti, njihov skalarni proizvod je nula. I ovako se skalarni proizvod izražava kroz koordinate vektora i .

Linearna kombinacija vektora

Linearna kombinacija vektora zove se vektor

Gdje - koeficijenti linearne kombinacije. Ako kombinacija se naziva trivijalna ako je netrivijalna.

16 .Skalarni proizvod aritmetičkih vektora. Dužina vektora i ugao između vektora. Koncept vektorske ortogonalnosti.

Skalarni proizvod vektora a i b je broj

Skalarni proizvod se koristi za izračunavanje: 1) pronalaženja ugla između njih; 2) pronalaženja projekcije vektora; 3) izračunavanja dužine vektora; 4) uslova okomitosti vektora.

Dužina segmenta AB naziva se rastojanje između tačaka A i B. Ugao između vektora A i B naziva se ugao α = (a, b), 0≤ α ≤P. Po kojem trebate rotirati 1 vektor tako da se njegov smjer poklapa s drugim vektorom. Pod uslovom da im se porijeklo poklapa.

Ortom a je vektor a koji ima jediničnu dužinu i smjer a.

17. Sistem vektora i njegova linearna kombinacija. Koncept linearne zavisnosti i nezavisnosti sistema vektora. Teorema o potrebnim i dovoljnim uslovima za linearnu zavisnost sistema vektora.

Sistem vektora a1,a2,...,an naziva se linearno zavisnim ako postoje brojevi λ1,λ2,...,λn takvi da je barem jedan od njih različit od nule i λ1a1+λ2a2+...+λnan=0 . Inače, sistem se naziva linearno nezavisnim.

Dva vektora a1 i a2 nazivaju se kolinearni ako su im smjerovi isti ili suprotni.

Tri vektora a1, a2 i a3 nazivaju se komplanarnim ako su paralelni nekoj ravni.

Geometrijski kriterijumi za linearnu zavisnost:

a) sistem (a1,a2) je linearno zavisan ako i samo ako su vektori a1 i a2 kolinearni.

b) sistem (a1,a2,a3) je linearno zavisan ako i samo ako su vektori a1,a2 i a3 koplanarni.

teorema. (Neophodan i dovoljan uslov za linearnu zavisnost sistemima vektori.)

Vektorski sistem vektor prostor je linearno zavisno ako i samo ako je jedan od vektora sistema linearno izražen u terminima ostalih vektor ovaj sistem.

Zaključak 1. Sistem vektora u vektorskom prostoru je linearno nezavisan ako i samo ako nijedan od vektora sistema nije linearno izražen u terminima drugih vektora ovog sistema.2. Sistem vektora koji sadrži nulti vektor ili dva jednaka vektora je linearno zavisan.