Državna budžetska obrazovna ustanova

Samara region srednje opšte obrazovanje

Škola br. 2 nazvana po. V. Maskina pruga Art. Klyavlino

Općinski okrug Klyavlinsky

Samara region

« Jednačine

I

nejednakosti

sa parametrima"

tutorial

Klyavlino

Tutorial

"Jednačine i nejednačine sa parametrima" za učenike 10–11 razreda

ovaj priručnik je dodatak programu izbornog predmeta „Jednačine i nejednačine sa parametrima“ koji je položio eksterni ispit (naučno-metodološko stručno vijeće Ministarstva prosvjete i nauke Samarske regije od 19. decembra 2008. preporučilo je za upotreba u obrazovnim institucijama Samarske regije)

Autori

Romadanova Irina Vladimirovna

nastavnik matematike u srednjoškolskoj ustanovi Klyavlinskaya

Škola br. 2 nazvana po. V. Maskina, Kljavlinski okrug, Samarska oblast

Serbaeva Irina Aleksejevna

Uvod………………………………………………………………………3-4

Linearne jednadžbe i nejednačine s parametrima……………..4-7

Kvadratne jednadžbe i nejednačine s parametrima……………7-9

Frakcijsko-racionalne jednadžbe s parametrima……………..10-11

Iracionalne jednačine i nejednačine sa parametrima……11-13

Trigonometrijske jednadžbe i nejednačine sa parametrima.14-15

Eksponencijalne jednadžbe i nejednačine sa parametrima………16-17

Logaritamske jednadžbe i nejednačine s parametrima......16-18

Ciljevi Jedinstvenog državnog ispita…………………………………………………………...18-20

Zadaci za samostalan rad……………………………21-28

Uvod.

Jednačine i nejednačine s parametrima.

Ako u jednadžbi ili nejednakosti nekim koeficijentima nisu date određene numeričke vrijednosti, već su označeni slovima, tada se nazivaju parametri, i sama jednadžba ili nejednakost parametarski.

Da biste riješili jednačinu ili nejednačinu s parametrima potrebno je:

Odaberite posebno značenje- ovo je vrijednost parametra u kojem ili prilikom prolaska kroz koji se mijenja rješenje jednadžbe ili nejednačine.

Definiraj važeće vrijednosti– to su vrijednosti parametra kod kojih jednačina ili nejednakost imaju smisla.

Rješavanje jednadžbe ili nejednakosti s parametrima znači:

1) odrediti pri kojim vrijednostima parametara postoje rješenja;

2) za svaki dozvoljeni sistem vrednosti parametara pronaći odgovarajući skup rešenja.

Jednačinu s parametrom možete riješiti koristeći sljedeće metode: analitičke ili grafičke.

Analitička metoda uključuje zadatak proučavanja jednačine razmatranjem nekoliko slučajeva, od kojih se nijedan ne može propustiti.

Rješavanje jednadžbi i nejednačina sa parametrima svake vrste analitičkom metodom podrazumijeva detaljnu analizu situacije i konzistentno istraživanje, pri čemu se javlja potreba "pažljivo rukovanje" sa parametrom.

Grafička metoda uključuje konstruiranje grafa jednadžbe, iz kojeg se može odrediti kako promjena parametra utječe na rješenje jednačine, respektivno. Grafikon vam ponekad omogućava da analitički formulirate potrebne i dovoljne uvjete za rješavanje problema. Metoda grafičkog rješenja je posebno efikasna kada trebate ustanoviti koliko korijena ima jednačina u zavisnosti od parametra i ima nesumnjivu prednost što se to jasno vidi.

§ 1. Linearne jednačine i nejednačine.

Linearna jednadžba A x = b , napisan u opštem obliku, može se posmatrati kao jednačina sa parametrima, gde x – nepoznato , a , b - opcije. Za ovu jednačinu, posebna ili kontrolna vrijednost parametra je ona pri kojoj koeficijent nepoznate postaje nula.

Prilikom rješavanja linearne jednadžbe s parametrom razmatraju se slučajevi kada je parametar jednak svojoj posebnoj vrijednosti i različit od nje.

Posebna vrijednost parametra a je vrijednost A = 0.

b = 0 je posebna vrijednost parametra b .

At b ¹ 0 jednačina nema rješenja.

At b = 0 jednačina će poprimiti oblik: 0x = 0. Rješenje ove jednačine je bilo koji realan broj.

Nejednakosti oblika ah > b I sjekira < b (a ≠ 0) nazivaju se linearne nejednačine. Skup rješenja nejednakosti ah >b– interval

(; +), Ako a > 0 , And (-;) , Ako A< 0 . Slično za nejednakost

Oh< b skup rješenja - interval(-;), Ako a > 0, I (; +), Ako A< 0.

Primjer 1. Riješite jednačinu sjekira = 5

Rješenje: Ovo je linearna jednačina.

Ako a = 0, zatim jednačina 0 × x = 5 nema rješenje.

Ako A¹ 0, x =- rješenje jednačine.

Odgovori: at A¹ 0, x=

za a = 0 nema rješenja.

Primjer 2. Riješite jednačinu sjekira – 6 = 2a – 3x.

Rješenje: Ovo je linearna jednadžba, sjekira – 6 = 2a – 3x (1)

ax + 3x = 2a +6

Prepisivanje jednačine kao (a+3)x = 2(a+3), razmotrite dva slučaja:

a= -3 I A¹ -3.

Ako a= -3, zatim bilo koji realan broj X je korijen jednačine (1). Ako A¹ -3 , jednačina (1) ima jedan korijen x = 2.

odgovor: At a = -3, x R ; at A ¹ -3, x = 2.

Primjer 3. Na kojim vrijednostima parametara A među korijenima jednačine

2ah – 4kh – a 2 + 4a – 4 = 0 ima više korijena 1 ?

Rješenje: Hajde da riješimo jednačinu 2ah – 4kh – a 2 + 4a – 4 = 0– linearna jednačina

2(a - 2) x = a 2 – 4a +4

2(a - 2) x = (a – 2) 2

At a = 2 rješavanje jednačine 0x = 0 bit će bilo koji broj, uključujući onaj veći od 1.

At A¹ 2 x =
. Po uslovu x > 1, to je
>1 i >4.

odgovor: At A (2) U (4;∞).

Primjer 4 . Za svaku vrijednost parametra A pronaći broj korijena jednadžbe ah=8.

Rješenje. sjekira = 8– linearna jednačina.

y = a– porodica horizontalnih linija;

y = - Graf je hiperbola. Napravimo grafove ovih funkcija.

Odgovor: Ako a =0, tada jednačina nema rješenja. Ako a ≠ 0, tada jednačina ima jedno rješenje.

Primjer 5 . Pomoću grafikona saznajte koliko korijena ima jednačina:

|x| = ah – 1.

y =| x | ,

y = ah – 1– grafik je prava linija koja prolazi kroz tačku (0;-1).

Napravimo grafove ovih funkcija.

Odgovor: Kada |a|>1- jedan koren

at | a|≤1 – jednačina nema korijena.

Primjer 6 . Riješite nejednakost sjekira + 4 > 2x + a 2

Rješenje : sjekira + 4 > 2x + a 2
(a – 2) x >A 2 – 4. Razmotrimo tri slučaja.

Odgovori. x > a + 2 at a > 2; X<а + 2, at A< 2; at a=2 nema rješenja.

§ 2. Kvadratne jednačine i nejednačine

Kvadratna jednadžba je jednadžba oblika Oh ² + b x + c = 0 , Gdje a≠ 0,

A, b , With - opcije.

Da biste riješili kvadratne jednadžbe s parametrom, možete koristiti standardne metode rješenja koristeći sljedeće formule:

1 ) diskriminanta kvadratne jednadžbe: D = b ² - 4 ac , (
²- ac)

2) formule za korijene kvadratne jednadžbe:X 1 =
, X 2 =
,

(X 1,2 =
)

Kvadratne nejednakosti se nazivaju

a X 2 + b x + c > 0,a X 2 + b x + c< 0, (1), (2)

a X 2 + b x + c ≥ 0,a X 2 + b x + c ≤ 0,(3), (4)

Skup rješenja nejednačine (3) dobiva se kombiniranjem skupova rješenja nejednačine (1) i jednadžbe , a X 2 + b x + c = 0. Slično se može naći i skup rješenja nejednakosti (4).

Ako je diskriminant kvadratnog trinoma a X 2 + b x + c je manji od nule, tada je za a > 0 trinom pozitivan za sve x R.

Ako kvadratni trinom ima korijen (x 1 < х 2 ), tada je za a > 0 pozitivan na skupu(-; x 2 )
(X 2; +) i negativan na intervalu

(x 1; x 2 ). Ako a< 0, то трехчлен положителен на интервале (х 1 ; x 2 ) i negativan za sve x (-; x 1 )
(X 2; +).

Primjer 1. Riješite jednačinu ax² - 2 (a – 1)x – 4 = 0.

Ovo je kvadratna jednadžba

Rješenje: Posebno značenje a = 0.

At a = 0 dobijamo linearnu jednačinu 2x – 4 = 0. Ima jedan korijen x = 2.

At a ≠ 0. Hajde da nađemo diskriminanta.

D = (a-1)² + 4a = (a+1)²

Ako a = -1, To D = 0 - jedan koren.

Pronađimo korijen zamjenom a = -1.

-x² + 4x – 4= 0, to je x² -4x + 4 = 0, nalazimo to x=2.

Ako a ≠ - 1, To D >0 . Koristeći formulu korijena dobijamo:x=
;

X 1 =2, x 2 = -.

odgovor: At a=0 i a= -1 jednadžba ima jedan korijen x = 2; at a ≠ 0 i

A ≠ - 1 jednadžba ima dva korijenaX 1 =2, x 2 =-.

Primjer 2. Pronađite broj korijena ove jednadžbe x²-2x-8-a=0 ovisno o vrijednostima parametara A.

Rješenje. Prepišimo ovu jednačinu u obliku x²-2x-8=a

y = x²-2x-8- graf je parabola;

y =a- porodica horizontalnih linija.

Napravimo grafove funkcija.

Odgovor: Kada A<-9 , jednačina nema rješenja; kada je a=-9, jednačina ima jedno rješenje; at a>-9, jednačina ima dva rješenja.

Primjer 3. Na šta A nejednakost (a – 3) x 2 – 2ax + 3a – 6 >0 vrijedi za sve vrijednosti x?

Rješenje. Kvadratni trinom je pozitivan za sve vrijednosti x if

a-3 > 0 i D<0, т.е. при а, удовлетворяющих системе неравенств

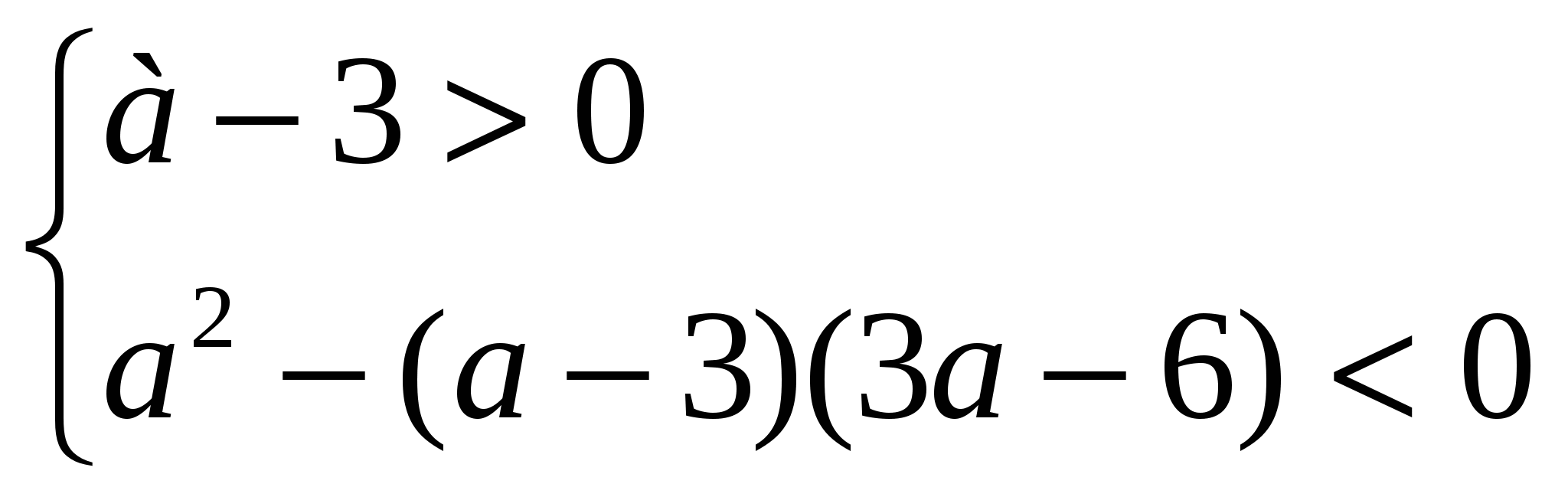
, odakle to sledia > 6 .

Odgovori.a > 6

§ 3. Frakcionalne racionalne jednadžbe sa parametrom,

svodiv na linearnu

Proces rješavanja frakcijskih jednadžbi provodi se prema uobičajenoj shemi: razlomak se zamjenjuje cijelim brojem množenjem obje strane jednadžbe sa zajedničkim nazivnikom njene lijeve i desne strane. Nakon čega se rješava cijela jednačina, isključujući strane korijene, odnosno brojeve koji imenilac pretvaraju u nulu.

U slučaju jednačina sa parametrom, ovaj problem je složeniji. Ovdje je, da bi se „eliminirali“ strani korijeni, potrebno pronaći vrijednost parametra koji pretvara zajednički nazivnik na nulu, odnosno riješiti odgovarajuće jednadžbe za parametar.

Primjer 1. Riješite jednačinu
= 0

Rješenje: D.Z: x +2 ≠ 0, x ≠ -2

x – a = 0, x = a.

odgovor: At a ≠ - 2, x=a

At a = -2 nema korena.

Primjer 2 . Riješite jednačinu
-
=
(1)

Ovo je frakciona racionalna jednačina

Rješenje: Značenje a = 0 je poseban. At a = 0 jednadžba nema smisla i stoga nema korijen. Ako a ≠ 0, tada će nakon transformacije jednadžba poprimiti oblik: x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- kvadratna jednačina.

Hajde da nađemo diskriminanta = (1 – a)² - (a² - 2a – 3)= 4, pronađite korijene jednačineX 1 = a + 1, x 2 = a - 3.

Prilikom prelaska sa jednačine (1) na jednačinu (2), proširio se domen definicije jednačine (1), što bi moglo dovesti do pojave stranih korijena. Stoga je verifikacija neophodna.

Ispitivanje. Isključimo iz pronađenih vrijednosti X one u kojima

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

Ako X 1 +1=0, to je (a+1) + 1= 0, To a= -2. dakle,

at a= -2 , X 1 -

Ako X 1 +2=0, to je (a+1)+2=0, To a = - 3. Dakle, kada a = - 3, x 1 - vanjski korijen jednadžbe. (1).

Ako X 2 +1=0, to je (a – 3) + 1= 0, To a = 2. Dakle, kada a = 2 x 2 - vanjski korijen jednačine (1).

Ako X 2 +2=0, to je ( a – 3) + 2 = 0, To a=1. Dakle, kada a = 1,

X 2 - vanjski korijen jednačine (1).

U skladu sa ovim, kada a = - 3 dobijamo x = - 3 – 3 = -6;

at a = - 2 x = -2 – 3= - 5;

at a = 1 x =1 + 1= 2;

at a = 2 x = 2+1 = 3.

Možete zapisati odgovor.

odgovor: 1) ako a= -3, To x= -6; 2) ako a= -2, To x= -5; 3) ako a= 0, tada nema korijena; 4) ako a= 1, To x=2; 5) ako a=2, To x=3; 6) ako a ≠ -3, a ≠ -2, a ≠ 0, a≠ 1, a ≠ 2, zatim x 1 = a + 1, x 2 = a-3.

§4. Iracionalne jednačine i nejednačine

Pozivaju se jednadžbe i nejednačine u kojima se varijabla nalazi pod predznakom korijena iracionalno.

Rješavanje iracionalnih jednadžbi svodi se na prelazak s iracionalne na racionalnu jednačinu eksponencijalnom eksponencijalnom bojom obje strane jednačine ili zamjenom varijable. Kada se obje strane jednačine podignu na parni stepen, mogu se pojaviti strani korijeni. Stoga, kada koristite ovu metodu, trebali biste provjeriti sve pronađene korijene tako što ćete ih zamijeniti u originalnu jednadžbu, uzimajući u obzir promjene u vrijednostima parametara.

Jednačina oblika
=g (x) je ekvivalentan sistemu

Nejednakost f (x) ≥ 0 proizlazi iz jednačine f (x) = g 2 (x).

Prilikom rješavanja iracionalnih nejednakosti koristit ćemo sljedeće ekvivalentne transformacije:

≤ g(x)


≥g(x)

Primjer 1. Riješite jednačinu
= x + 1 (3)

Ovo je iracionalna jednadžba

Rješenje: Po definiciji aritmetičkog korijena, jednačina (3) je ekvivalentna sistemu
.

At a = 2 prva jednačina sistema ima oblik 0 x = 5, odnosno nema rješenja.

At a≠ 2 x=
. Hajde da saznamo na kojim vrednostimaA pronađena vrijednostX zadovoljava nejednakostx ≥ -1:
≥ - 1,
≥ 0,

gdje a ≤ ili a > 2.

odgovor: At a≤, a > 2 x=
, at < а ≤ 2 jednačina nema rješenja.

Primjer 2. Riješite jednačinu
= a (Dodatak 4)

Rješenje. y =

y = a– porodica horizontalnih linija.

Napravimo grafove funkcija.

Odgovori: at A<0 – nema rješenja;

at A≥ 0 - jedno rešenje.

Primjer 3 . Hajde da riješimo nejednakost(a+1)
<1.

Rješenje. O.D.Z. x ≤ 2. Ako a+1 ≤0, tada nejednakost vrijedi za sve dopuštene vrijednosti X. Ako a+1>0, To

(a+1)
<1.

<

gdje X (2-
2

Odgovori. X (- ;2at a (-;-1, X (2-
2

at A (-1;+).

§ 5. Trigonometrijske jednačine i nejednačine.

Evo formula za rješavanje najjednostavnijih trigonometrijskih jednadžbi:

Sinx = a
x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = a
x = ±arccos a + 2 πn, n Z, ≤1. (2)

Ako >1, tada jednačine (1) i (2) nemaju rješenja.

tan x = a
x= arctan a + πn, n Z, a R

ctg x = a
x = arcctg a + πn, n Z, a R

Za svaku standardnu ​​nejednačinu označavamo skup rješenja:

1. sin x > a
arcsin a + 2 πn Z,

at a <-1, x R ; at a ≥ 1, nema rješenja.

2. . sin x< a
π - arcsin a + 2 πnZ,

za a≤-1, nema rješenja; za a > 1,x R

3. cos x > a
- arccos a + 2 πn < x < arccos a + 2 πn , n Z ,

at A<-1, x R ; at a ≥ 1 , nema rješenja.

4. cos x arccos a+ 2 πnZ,

at a≤-1 , nema rješenja; ata > 1, x R

5. tan x > a, arctan a + πnZ

6.tg x< a, -π/2 + πn Z

Primjer 1. Nađi A, za koje ova jednadžba ima rješenje:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Rješenje. Zapišimo jednačinu u formu

Withos 2 x + (2 a -4) cosx +(a – 5)(a+1) =0, rješavajući ga kao kvadrat, dobijamo cosx = 5-A I cosx = -a-1.

Jednačina cosx = 5- A ima rješenja -1≤ 5-A ≤1
4≤ A≤ 6, a jednad. cosx = - a-1 pod uvjetom -1≤ -1-A ≤ 1
-2 ≤ A ≤0.

Odgovori. A -2; 0
4; 6

Primjer 2. Na šta bpostoji takva da je nejednakost
+ b> 0 važi za sve x ≠πn , n Z .

Rješenje. Hajde da stavimo A= 0. Nejednakost vrijedi za b >0. Pokažimo sada da nijedan b ≤0 ne zadovoljava uslove problema. Zaista, dovoljno je staviti x = π /2, Ako A <0, и х = - π /2 at A ≥0.

Odgovori.b>0

§ 6. Eksponencijalne jednačine i nejednačine

1. Jednačina h(x) f ( x ) = h(x) g ( x) at h(x) > 0 je ekvivalentno kolekciji od dva sistema
I

2. U posebnom slučaju (h (x)= a ) jednačina A f(x) = A g(x) na A> 0, ekvivalentno je kolekciji dva sistema

I

3. Jednačina A f(x) = b , Gdje A > 0, a ≠1, b>0, što je ekvivalentno jednačini

f (x )= log a b. Dešava se A=1 se razmatraju odvojeno.

Rješenje najjednostavnijih eksponencijalnih nejednakosti zasniva se na svojstvu snage. Nejednakost oblikaf(a x ) > 0 koristeći promjenu varijablet= a x svodi na rješavanje sistema nejednakosti
a zatim na rješavanje odgovarajućih jednostavnih eksponencijalnih nejednačina.

Prilikom rješavanja nestroge nejednačine potrebno je skupu rješenja stroge nejednakosti dodati korijene odgovarajuće jednadžbe. Kao i kod rješavanja jednadžbi u svim primjerima koji sadrže izraz A f (x), pretpostavljamo A> 0. Slučaj A= 1 se razmatraju odvojeno.

Primjer 1 . Na šta A jednačina 8 x =
ima samo pozitivne korene?

Rješenje. Po svojstvu eksponencijalne funkcije s bazom većom od jedan, imamo x>0
8 X >1

>1

>0, odaklea (1,5;4).

Odgovori. a (1,5;4).

Primjer 2. Riješite nejednakost a 2 ∙2 x > a

Rješenje. Razmotrimo tri slučaja:

1. A< 0 . Budući da je lijeva strana nejednakosti pozitivna, a desna negativna, nejednakost vrijedi za bilo koji x R.

2. a=0. Nema rješenja.

3. A > 0 . a 2 ∙2 x > a
2 x >
x > -log 2 a

Odgovori. X R at A > 0; nema rješenja za a =0; X (- log 2 a; +) ata> 0 .

§ 7. Logaritamske jednačine i nejednačine

Predstavimo neke ekvivalencije koje se koriste u rješavanju logaritamske jednačine i nejednačine.

1. Jednačina log f (x) g (x) = log f (x) h (x) je ekvivalentna sistemu

Konkretno, ako A >0, A≠1, onda

log a g(x)=log a h(x)

2. Jednačina log a g(x)=b
g(x)=a b ( A >0, a ≠ 1, g(x) >0).

3. Nejednakost log f ( x ) g (x) ≤ log f ( x ) h(x) je ekvivalentno kombinaciji dva sistema:
I

ako a, b su brojevi, a >0, a ≠1, onda

log a f(x) ≤ b

log a f(x)>b

Primjer 1. Riješite jednačinu

Rješenje. Nađimo ODZ: x > 0, x ≠ A 4 , a > 0, A≠ 1. Transformirajte jednačinu

log x – 2 = 4 – log a x
log x + log a x– 6 = 0, odakle log a x = - 3

x = A-3 i log a x = 2
x = A 2. Uslov x = A 4
A – 3 = A 4 ili A 2 = A 4 se ne izvodi na ODZ.

odgovor: x = A-3, x = A 2 at A (0; 1)
(1; ).

Primjer 2 . Pronađite najveću vrijednost A, za koje je jednadžba

2 log -
+ a = 0 ima rješenja.

Rješenje. Napravićemo zamjenu
= ti dobijamo kvadratnu jednačinu 2t 2 – t + a = 0. Rješavanje, nalazimoD = 1-8 a . Hajde da razmotrimo D≥0, 1-8 A ≥0
A ≤.

At A = kvadratna jednadžba ima korijent= >0.

Odgovori. A =

Primjer 3 . Riješite nejednakostlog(x 2 – 2 x + a ) > - 3

Rješenje. Hajde da rešimo sistem nejednačina

Korijeni kvadratnih trinoma x 1,2 = 1 ±
njihov 3,4 = 1 ±
.

Vrijednosti kritičnih parametara: A= 1 i A= 9.

Neka su X 1 i X 2 skupovi rješenja prve i druge nejednačine

X 1
X 2 = X – rješenje izvorne nejednačine.

U 0< a <1 Х 1 = (- ;1 -
)
(1 +
; +), atA> 1 X 1 = (-;+).

U 0< a < 9 Х 2 = (1 -
; 1 +
), atA≥9 X 2 – nema rješenja.

Razmotrimo tri slučaja:

1. 0< a ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < a < 9 Х = (1 -
;1 +
).

3. a≥ 9 X – nema rješenja.

Ciljevi Jedinstvenog državnog ispita

Visok nivo C1, C2

Primjer 1. Pronađite sve vrijednosti R, za koje je jednadžba

R ∙ ctg 2x+2sinx+ str= 3 ima najmanje jedan korijen.

Rješenje. Hajde da transformišemo jednačinu

R ∙ (
- 1) + 2sinx + str= 3, sinx =t, t
, t 0.

- str+2t+ str = 3, + 2 t = 3, 3 -2t = , 3t 2 – 2t 3 = str .

Neka f(y) = 3 t 2 – 2 t 3 . Nađimo skup vrijednosti funkcijef(x) uključeno


. at / = 6 t – 6 t 2 , 6 t - 6 t 2 = 0, t 1 =0, t 2 = 1. f(-1) = 5, f(1) = 1.

At t
, E(f) =
,

At t
, E(f) =
, odnosno kada t


, E(f) =
.

Za jednačinu 3t 2 – 2 t 3 = str (dakle dato) je imao barem jedan korijen potreban i dovoljanstr E(f), to je str
.

Odgovori.
.

Primjer 2.

Na kojim vrijednostima parametaraA jednačina log
(4 x 2 – 4 a + a 2 +7) = 2 ima tačno jedan korijen?

Rješenje. Hajde da transformišemo jednačinu u jednu ekvivalentnu ovoj:

4x 2 – 4 a + a 2 +7 = (x 2 + 2) 2.

Imajte na umu da ako je određeni broj x korijen rezultirajuće jednačine, onda je broj – x također korijen ove jednačine. Po uslovu, to nije izvodljivo, pa je jedini korijen broj 0.

Naći ćemo A.

4∙ 0 2 - 4a + a 2 +7 = (0 2 + 2) 2 ,

a 2 - 4a +7 = 4, a 2 - 4a +3 = 0, a 1 = 1, a 2 = 3.

Ispitivanje.

1) a 1 = 1. Tada jednačina izgleda ovako:log
(4 x 2 +4) =2. Hajde da to rešimo

4x 2 + 4 = (x 2 + 2) 2, 4x 2 + 4 = x 4 + 4x 2 + 4, x 4 = 0, x = 0 je jedini korijen.

2) a 2 = 3. Jednačina izgleda ovako:log
(4 x 2 +4) =2
x = 0 je jedini korijen.

Odgovori. 1; 3

Visok nivo C4, C5

Primjer 3. Pronađite sve vrijednosti R, za koje jednačina

x 2 – ( R+ 3)x + 1= 0 ima cjelobrojne korijene i ovi korijeni su rješenja nejednakosti: x 3 – 7 R x 2 + 2x 2 – 14 R x - 3x +21 R ≤ 0.

Rješenje. Neka x 1, X 2 – cjelobrojni korijeni jednačine x 2 – (R + 3)x + 1= 0. Tada su, prema Vietovoj formuli, jednakosti x 1 + x 2 = R + 3, x 1 ∙ x 2 = 1. Proizvod dva cijela broja x 1 , X 2 može biti jednako jedan samo u dva slučaja: x 1 = x 2 = 1 ili x 1 = x 2 = - 1. Ako je x 1 = x 2 = 1, ondaR + 3 = 1+1 = 2
R = - 1; ako je x 1 = x 2 = - 1, ondaR + 3 = - 1 – 1 = - 2
R = - 5. Provjerimo da li su korijeni jednadžbe x 2 – (R + 3)x + 1= 0 u opisanim slučajevima rješenjima ove nejednakosti. Za tu prilikuR = - 1, x 1 = x 2 = 1 imamo

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – tačno; za tu priliku R= - 5, x 1 = x 2 = - 1 imamo (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 – tačno. Dakle, ispunjeni su samo uslovi problema R= - 1 i R = - 5.

Odgovori.R 1 = - 1 i R 2 = - 5.

Primjer 4. Pronađite sve pozitivne vrijednosti parametra A, za koji broj 1 pripada domeni definicije funkcije

at = (A
- A
).

Vrsta posla: 18

Stanje

Za koje vrijednosti parametra a vrijedi nejednakost

\log_(5)(4+a+(1+5a^(2)-\cos^(2)x) \cdot\sin x - a \cos 2x) \leq 1 je zadovoljen za sve vrijednosti x?

Pokaži rješenje

Rješenje

Ova nejednakost je ekvivalentna dvostrukoj nejednakosti 0 < 4+a+(5a^{2}+\sin^{2}x) \sin x+ a(2 \sin^(2)x-1) \leq 5 .

Neka \sin x=t , tada dobijamo nejednakost:

4 < t^{3}+2at^{2}+5a^{2}t \leq 1 \: (*) , koji se mora izvršiti za sve vrijednosti -1 \leq t \leq 1 . Ako je a=0, onda nejednakost (*) vrijedi za bilo koji t\in [-1;1] .

Neka je \neq 0 . Funkcija f(t)=t^(3)+2at^(2)+5a^(2)t raste na intervalu [-1;1] , budući da je izvod f"(t)=3t^(2) +4at +5a^(2) > 0 za sve vrijednosti t \in \mathbb(R) i \neq 0 (diskriminanta D< 0 и старший коэффициент больше нуля).

Nejednakost (*) će biti zadovoljena za t \in [-1;1] pod uslovima

\begin(slučajevi) f(-1) > -4, \\ f(1) \leq 1, \\ a \neq 0; \end(cases)\: \Leftrightarrow \begin(slučajevi) -1+2a-5a^(2) > -4, \\ 1+2a+5a^(2) \leq 1, \\ a \neq 0; \end(cases)\: \Leftrightarrow \begin(slučajevi) 5a^(2)-2a-3< 0, \\ 5a^{2}+2a \leq 0, \\ a \neq 0; \end{cases}\: \Leftrightarrow -\frac(2)(5)\leq a< 0 .

Dakle, uslov je zadovoljen kada je -\frac(2)(5) \leq a \leq 0 .

Odgovori

\levo [ -\frac(2)(5); 0\desno ]

Izvor: „Matematika. Priprema za Jedinstveni državni ispit 2016. Nivo profila." Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Vrsta posla: 18
Tema: Nejednakosti sa parametrom

Stanje

Pronađite sve vrijednosti parametra a, za svaku od njih nejednakost

x^2+3|x-a|-7x\leqslant -2a

ima jedinstveno rešenje.

Pokaži rješenje

Rješenje

Nejednakost je ekvivalentna skupu sistema nejednakosti

\left[\!\!\begin(niz)(l) \begin(cases) x \geqslant a, \\ x^2+3x-3a-7x+2a\leqslant0; \end(slučajevi) \\ \begin(slučajevi)x \left[\!\!\begin(array)(l) \begin(cases) x \geqslant a, \\ x^2-4x-a\leqslant0; \end(slučajevi) \\ \begin(slučajevi)x \left[\!\!\begin(array)(l) \begin(cases) a \leqslant x, \\ a\geqslant x^2-4x; \end(slučajevi) \\ \begin(slučajevi)a>x, \\ a\leqslant -\frac(x^2)(5)+2x. \end(slučajevi)\end(niz)\desno.

U Oxa koordinatnom sistemu ćemo konstruisati grafove funkcija a=x, a=x^2-4x, a=-\frac(x^2)(5)+2x.

Rezultirajući skup je zadovoljen točkama koje su zatvorene između grafova funkcija a=x^2-4x, a=-\frac(x^2)(5)+2x na intervalu x\in (osenčeno područje).

Iz grafa utvrđujemo: originalna nejednačina ima jedinstveno rješenje za a=-4 i a=5, budući da će u osenčenom području postojati jedna tačka sa ordinatom a jednakom -4 i 5.

Rad na kursu

Izvođač: Bugrov S K.

Proučavanje mnogih fizičkih procesa i geometrijskih obrazaca često dovodi do rješavanja problema s parametrima. Neki univerziteti u ispitne radove uključuju i jednačine, nejednakosti i njihove sisteme, koji su često vrlo složeni i zahtijevaju nestandardan pristup rješavanju. U školi se ovaj jedan od najtežih dijelova školskog predmeta matematike razmatra samo u nekoliko izbornih časova.

Pripremajući ovaj rad, postavio sam za cilj dublje proučavanje ove teme, identificirajući najracionalnije rješenje koje brzo vodi do odgovora. Po mom mišljenju, grafička metoda je zgodan i brz način rješavanja jednačina i nejednačina sa parametrima.

U svom eseju govorim o tipovima jednačina, nejednačinama i njihovim sistemima koji se često susreću, a nadam se da će mi znanje koje sam stekao u radu pomoći pri polaganju školskih ispita i pri upisu na fakultet.

§ 1. Osnovne definicije

Razmotrite jednačinu

¦(a, b, c, …, k, x)=j(a, b, c, …, k, x), (1)

gdje su a, b, c, …, k, x promjenjive veličine.

Bilo koji sistem varijabilnih vrijednosti

a = a0, b = b0, c = c0, …, k = k0, x = x0,

u kojem i lijeva i desna strana ove jednačine uzimaju realne vrijednosti naziva se sistem dozvoljenih vrijednosti varijabli a, b, c, ..., k, x. Neka je A skup svih dozvoljenih vrednosti a, B skup svih dozvoljenih vrednosti b, itd., X skup svih dozvoljenih vrednosti x, tj. aOA, bOB, …, xOX. Ako za svaki od skupova A, B, C, …, K odaberemo i fiksiramo, redom, jednu vrijednost a, b, c, …, k i zamijenimo ih u jednačinu (1), tada ćemo dobiti jednačinu za x, tj. jednačina sa jednom nepoznatom.

Varijable a, b, c, ..., k, koje se pri rješavanju jednačine smatraju konstantnim, nazivaju se parametri, a sama jednačina se naziva jednačina koja sadrži parametre.

Parametri su označeni prvim slovima latinične abecede: a, b, c, d, ..., k, l, m, n, a nepoznanice su označene slovima x, y, z.

Riješiti jednadžbu s parametrima znači naznačiti pri kojim vrijednostima parametara rješenja postoje i koja su.

Dvije jednadžbe koje sadrže iste parametre nazivaju se ekvivalentnim ako:

a) imaju smisla za iste vrijednosti parametara;

b) svako rješenje prve jednačine je rješenje druge i obrnuto.

§ 2. Algoritam rješenja.

Naći domen definicije jednačine.

Izražavamo a kao funkciju od x.

U xOa koordinatnom sistemu konstruišemo graf funkcije a=¦(x) za one vrednosti x koje su uključene u domen definicije ove jednačine.

Nalazimo tačke preseka prave a=c, gde je cÎ(-¥;+¥) sa grafikom funkcije a=¦(x).Ako prava a=c seče graf a=¦(x) , tada određujemo apscisu presječnih tačaka. Da biste to učinili, dovoljno je riješiti jednačinu a=¦(x) za x.

Zapisujemo odgovor.

I. Riješite jednačinu

(1)

Pošto x=0 nije korijen jednadžbe, jednačina se može riješiti za:

ili

Graf funkcije su dvije “slijepljene” hiperbole. Broj rješenja originalne jednačine određen je brojem presječnih tačaka konstruirane linije i prave linije y=a.

Ako je O (-¥;-1]P(1;+¥)P

, tada prava linija y=a siječe graf jednačine (1) u jednoj tački. Apscisu ove tačke ćemo pronaći kada rješavamo jednadžbu za x.

Dakle, na ovom intervalu jednačina (1) ima rješenje

. , tada prava linija y=a siječe grafik jednačine (1) u dvije tačke. Apscise ovih točaka mogu se naći iz jednadžbi i , Dobijamo i . , tada prava y=a ne siječe graf jednačine (1), stoga nema rješenja.

Ako je O (-¥;-1]P(1;+¥)P

, To ; , To , ; , onda nema rješenja.

II. Pronađite sve vrijednosti parametra a za koje je jednadžba

ima tri različita korijena.

Prepisivanje jednačine kao

i nakon što ste ispitali par funkcija, možete primijetiti da će željene vrijednosti parametra a i samo one odgovarati onim pozicijama grafa funkcije na kojima ima točno tri točke presjeka s grafom funkcije .

U koordinatnom sistemu xOy konstruisaćemo graf funkcije

). Da bismo to učinili, možemo je predstaviti u obliku i, nakon što smo razmotrili četiri slučaja, ovu funkciju zapišemo u obliku

Pošto je graf funkcije

- ovo je prava linija koja ima ugao nagiba prema osi Ox jednak , a sijekući osu Oy u tački s koordinatama (0, a), zaključujemo da se tri naznačene točke presjeka mogu dobiti samo u slučaju kada ova linija dodiruje graf funkcije. Dakle, nalazimo derivat.

III. Pronađite sve vrijednosti parametra a, za svaku od kojih je sistem jednadžbi

ima rješenja.

Iz prve jednačine sistema dobijamo

pri Prema tome, ova jednadžba definira familiju "poluparabola" - desne grane parabole "klize" sa svojim vrhovima duž ose apscise.

Odaberimo potpune kvadrate na lijevoj strani druge jednadžbe i faktorizirajmo je

Mnogo tačaka aviona

koje zadovoljavaju drugu jednačinu su dvije prave i

Otkrijmo pri kojim vrijednostima parametra a kriva iz porodice "semiparabola" ima barem jednu zajedničku tačku s jednom od rezultirajućih pravih linija.

Rješavanje nejednačina s parametrom.

Nejednačine koje imaju oblik ax > b, ax< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются linearne nejednakosti.

Principi rješavanja linearnih nejednačina s parametrom su vrlo slični principima rješavanja linearnih jednačina s parametrom.

Primjer 1.

Riješite nejednačinu 5x – a > ax + 3.

Rješenje.

Prvo, transformirajmo originalnu nejednakost:

5x – ax > a + 3, izvadimo x iz zagrada na lijevoj strani nejednačine:

(5 – a)x > a + 3. Sada razmotrite moguće slučajeve za parametar a:

Ako je a > 5, onda je x< (а + 3) / (5 – а).

Ako je a = 5, onda nema rješenja.

Ako a< 5, то x >(a + 3) / (5 – a).

Ovo rješenje će biti odgovor na nejednakost.

Primjer 2.

Riješite nejednačinu x(a – 2) / (a ​​– 1) – 2a/3 ≤ 2x – a za a ≠ 1.

Rješenje.

Transformirajmo originalnu nejednakost:

x(a – 2) / (a ​​– 1) – 2x ≤ 2a/3 – a;

Ah/(a – 1) ≤ -a/3. Množenjem obe strane nejednakosti sa (-1) dobijamo:

ax/(a – 1) ≥ a/3. Hajde da istražimo moguće slučajeve za parametar a:

1 slučaj. Neka je a/(a – 1) > 0 ili a € (-∞; 0)ᴗ(1; +∞). Tada je x ≥ (a – 1)/3.

Slučaj 2. Neka je a/(a – 1) = 0, tj. a = 0. Tada je x bilo koji realan broj.

Slučaj 3. Neka je a/(a – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Odgovor: x € [(a – 1)/3; +∞) za € (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] za € (0; 1);
x € R za a = 0.

Primjer 3.

Riješite nejednačinu |1 + x| ≤ ax u odnosu na x.

Rješenje.

Iz uvjeta slijedi da desna strana ose nejednakosti mora biti nenegativna, tj. ax ≥ 0. Po pravilu otkrivanja modula iz nejednakosti |1 + x| ≤ ax imamo dvostruku nejednakost

Ax ≤ 1 + x ≤ ax. Prepišimo rezultat u obliku sistema:

(ax ≥ 1 + x;
(-ax ≤ 1 + x.

Hajde da ga transformišemo u:

((a – 1)x ≥ 1;
((a + 1)x ≥ -1.

Proučavamo rezultujući sistem na intervalima i tačkama (sl. 1):

Za a ≤ -1 x € (-∞; 1/(a – 1)].

Na -1< а < 0 x € [-1/(а – 1); 1/(а – 1)].

Kada je a = 0 x = -1.

U 0< а ≤ 1 решений нет.

Grafička metoda rješavanja nejednačina

Iscrtavanje grafova uvelike pojednostavljuje rješavanje jednadžbi koje sadrže parametar. Upotreba grafičke metode pri rješavanju nejednačina s parametrom je još jasnija i svrsishodnija.

Grafičko rješavanje nejednačina oblika f(x) ≥ g(x) znači pronalaženje vrijednosti varijable x za koje graf funkcije f(x) leži iznad grafika funkcije g(x). Da biste to učinili, uvijek je potrebno pronaći točke presjeka grafova (ako postoje).

Primjer 1.

Riješite nejednačinu |x + 5|< bx.

Rješenje.

Gradimo grafove funkcija y = |x + 5| i y = bx (sl. 2). Rješenje nejednakosti će biti one vrijednosti varijable x za koje je graf funkcije y = |x + 5| će biti ispod grafika funkcije y = bx.

Na slici je prikazano:

1) Za b > 1 prave se sijeku. Apscisa presečne tačke grafova ovih funkcija je rešenje jednačine x + 5 = bx, odakle je x = 5/(b – 1). Graf y = bx nalazi se iznad na x iz intervala (5/(b – 1); +∞), što znači da je ovaj skup rješenje nejednačine.

2) Slično nalazimo da je na -1< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) Za b ≤ -1 x € (-∞; 5/(b – 1)).

4) Za 0 ≤ b ≤ 1 grafovi se ne seku, što znači da nejednakost nema rješenja.

Odgovor: x € (-∞; 5/(b – 1)) za b ≤ -1;
x € (-5/(b + 1); 5/(b – 1)) na -1< b < 0;
nema rješenja za 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) za b > 1.

Primjer 2.

Riješite nejednačinu a(a + 1)x > (a + 1)(a + 4).

Rješenje.

1) Nađimo "kontrolne" vrijednosti za parametar a: a 1 = 0, i 2 = -1.

2) Rešimo ovu nejednakost na svakom podskupu realnih brojeva: (-∞; -1); (-1); (-10); (0); (0; +∞).

aa< -1, из данного неравенства следует, что х >(a + 4)/a;

b) a = -1, tada će ova nejednakost imati oblik 0 x > 0 – nema rješenja;

c) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, tada ova nejednakost ima oblik 0 x > 4 – nema rješenja;

e) a > 0, iz ove nejednakosti slijedi da je x > (a + 4)/a.

Primjer 3.

Riješite nejednakost |2 – |x||< a – x.

Rješenje.

Gradimo graf funkcije y = |2 – |x|| (sl. 3) i razmotriti sve moguće slučajeve položaja prave linije y = -x + a.

Odgovor: nejednakost nema rješenja za a ≤ -2;
x € (-∞; (a – 2)/2) za a € (-2; 2];
x € (-∞; (a + 2)/2) za a > 2.

Prilikom rješavanja različitih zadataka, jednačina i nejednačina s parametrima otkriva se značajan broj heurističkih tehnika koje se potom mogu uspješno primijeniti u bilo kojoj drugoj grani matematike.

Problemi sa parametrima igraju važnu ulogu u formiranju logičkog mišljenja i matematičke kulture. Zato ćete se, savladavši metode rješavanja problema s parametrima, uspješno nositi s drugim problemima.

Imate još pitanja? Ne znate kako riješiti nejednakosti?
Za pomoć od tutora -.
Prva lekcija je besplatna!

blog.site, pri kopiranju materijala u cijelosti ili djelimično, potrebna je veza do originalnog izvora.

Serija “Učenje rješavanja problema s parametrima”

IV. Kvadratne jednadžbe i nejednačine s parametrom

IV.1. Osnovni koncepti

Definicija. Funkcija oblika (1), gdje su , , date funkcije parametra A, razmatrana na presjeku njihovih domena definicije, nazvat će se kvadratnom funkcijom s parametrom A.

Primjeri.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

Definicija. Poddomena definicije kvadratne funkcije (1) s parametrom A razumjet ćemo cijeli skup parova vrijednosti X I A tip ( X; A), za svaki od kojih izraz ne gubi svoje značenje.

Uspostavimo domene definicije funkcija 1-10.

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

Ako parametar uzme jednu od numeričkih vrijednosti iz , tada će funkcija (1) poprimiti oblik jedne od funkcija s numeričkim koeficijentima:

; ; ;
; ; ; ,

Gdje k, b, c– realni brojevi.

Obratimo pažnju na činjenicu da za neke vrijednosti parametra iz, kvadratna funkcija s parametrom poprima oblik ili kvadratne funkcije bez parametra, ili linearne.

Budući da kvadratna funkcija s parametrom najčešće „generira“ porodicu kvadratnih ili linearnih funkcija s numeričkim koeficijentima, onda kada govorimo o grafovi kvadratne funkcije s parametrom, mislićemo na mnoge grafove ove porodice.

Definicija. A naziva se jednadžba oblika (1) gdje su , , ove funkcije parametra A, razmatrana na raskrsnici njihovih domena definicija.

Konkretno, neki od koeficijenata ili termin presjeka mogu biti brojevi.

Primjeri.

, (1)
, (2)
, (3)
, (4)
. (5)

Koristeći definiciju kvadratne funkcije s parametrom, možemo dati sljedeću definiciju kvadratne jednadžbe s parametrom.

Definicija. Kvadratna jednadžba s parametrom A naziva se jednadžba oblika , gdje je kvadratna funkcija s parametrom A.

Ako je , tada je jednadžba (1) kvadratna u tradicionalnom smislu, tj. drugi stepen.
Ako je , tada jednačina (1) postaje linearna.

Za sve važeće vrijednosti parametara A, za koje i , koristeći poznate formule dobijamo izraze za korijene jednadžbe (1) u smislu parametra.

Te vrijednosti A, u kojem , treba posebno razmatrati kao posebne slučajeve.
Tako će, na primjer, jednadžba (5) poprimiti oblik , odakle će .

IV.2. Kvadratne jednadžbe s parametrom

№1. Riješite jednačinu.

– jednačina-posljedica. Dobijamo: , .

U koordinatnom sistemu ( aoh) završavamo rješenje. (sl. 1)

Odgovor: 1. Ako , onda .

2. Ako , onda .

3. Ako , , onda , .

№2. Pronađite vrijednost parametra A, u kojem jednačina ima jedan korijen. Ako postoji nekoliko takvih vrijednosti, upišite njihov zbir u svoj odgovor.

Ova jednačina se svodi na ekvivalentan sistem:

Dovedemo ga u formu: i riješimo ga grafički u koordinatnom sistemu ( xOa). (Sl. 2).

Jednačina ima jedan korijen na , i .

№3. Pronađite sve vrijednosti X tako da za bilo koju vrijednost parametra A, koji ne pripada intervalu (0; 2], izraz nije jednak izrazu. (USE-2007).

Hajde da preformulišemo problem: „Pronađi sve vrednosti X takav da je za bilo koju vrijednost parametra jednadžba nema korena."
Hajde da se izrazimo A kroz X:

1) Neka . Onda . Stoga jednačina ima korijen. To znači da ne zadovoljava uslov.
2) Neka . Onda . Koristimo koordinatni sistem ( xOa). (Sl. 3).

Uslov je zadovoljen.

№4. Koliko korijena u zavisnosti od parametra A ima jednacinu?

Proširimo modul:

U koordinatnom sistemu ( xOy) napravimo graf funkcije

i nekoliko linija olovke paralelnih linija koje daje jednačina. (Sl. 4).

Odgovor: 1. Ako , onda nema korijena.

2. Ako , onda jedan korijen.

3. Ako , tada postoje dva korijena.

IV.3. Kvadratne nejednakosti s parametrom

№5. Riješite nejednakost .

1 način.

Uzmimo to u obzir. Tada je rješenje ove nejednakosti za bilo koje b.(Sl. 5).

Ako , onda prelazimo na nejednakost, čiji će skup rješenja biti prikazan u koordinatnom sistemu ( kutija). (Sl. 6).

Kombinirajmo fig. 5 i 6.

A sada prema sl. 7, rezajući ga vertikalnim ravnim linijama, lako je dobiti odgovor.

Odgovor: 1. Ako , onda .
2. Ako , onda .
3. Ako , onda

Metoda 2.

Rešimo nejednakost grafički u koordinatnom sistemu ( xOb):

. (Sl. 8).

Razmotrimo dva slučaja.

1) . Tada će nejednakost poprimiti oblik gdje je .
2) , zatim .

Grafikon funkcije i dio ravni koji sadrži tačke čije koordinate zadovoljavaju nejednakost prikazani su na slici 8.

1. Ako , onda .
2. Ako , onda . 3. Ako , onda .

3 way.

Predstavimo sada grafičko rješenje u koordinatnom sistemu ( xOy). Da bismo to učinili, proširimo modul:

Razmotrite funkciju .

Korijeni kvadratnog trinoma .

Uporedimo i .

1) , odakle .

Dobijamo totalitet. (sl. 9)

2) , odakle . (Sl. 10).

Tada tj. .

3) , odakle . (Sl. 11).

Tada tj. .

Odgovor: 1. Ako , onda .

2. Ako , onda .
3. Ako , onda .

№6. Pronađite sve vrijednosti parametara A, za koji je najmanja vrijednost funkcije više od 2.

Dovoljno je pronaći sve vrijednosti parametra A, za svaki od kojih je nejednakost istinita za bilo koju . Prepišimo nejednakost u obliku ., ;