Établissement d'enseignement budgétaire de l'État

Enseignement secondaire général de la région de Samara

École n°2 du nom. Chemin de fer V. Maskina Art. Kliavlino

District municipal de Kliavlinsky

Région de Samara

« Équations

Et

inégalités

avec paramètres"

Didacticiel

Kliavlino

Didacticiel

"Équations et inégalités avec paramètres" pour les élèves de la 10e à la 11e année

ce manuel est une annexe au programme du cours au choix « Équations et inégalités avec paramètres », qui a réussi un examen externe (le conseil d'experts scientifiques et méthodologiques du ministère de l'Éducation et des Sciences de la région de Samara en date du 19 décembre 2008 a recommandé pour utilisation dans les établissements d'enseignement de la région de Samara)

Auteurs

Romadanova Irina Vladimirovna

professeur de mathématiques à l'établissement d'enseignement secondaire Klyavlinskaya

École n°2 du nom. V. Maskina, district de Klyavlinsky, région de Samara

Serbaeva Irina Alekseevna

Introduction……………………………………………………………3-4

Équations linéaires et inégalités avec paramètres……………..4-7

Équations quadratiques et inégalités avec paramètres……………7-9

Équations fractionnaires-rationnelles avec paramètres……………..10-11

Équations irrationnelles et inégalités avec paramètres……11-13

Équations trigonométriques et inégalités avec paramètres.14-15

Équations exponentielles et inégalités avec paramètres………16-17

Équations logarithmiques et inégalités avec paramètres......16-18

Objectifs de l'examen d'État unifié………………………………………………………...18-20

Tâches pour le travail indépendant……………………………21-28

Introduction.

Équations et inégalités avec paramètres.

Si dans une équation ou une inégalité, certains coefficients ne reçoivent pas de valeurs numériques spécifiques, mais sont désignés par des lettres, alors ils sont appelés paramètres, et l'équation ou l'inégalité elle-même paramétrique.

Afin de résoudre une équation ou une inégalité avec des paramètres, vous devez :

Sélectionner sens spécial- c'est la valeur du paramètre dans lequel ou au passage par lequel la solution de l'équation ou de l'inégalité change.

Définir valeurs valides– ce sont les valeurs du paramètre pour lesquelles l’équation ou l’inégalité a un sens.

Résoudre une équation ou une inégalité avec des paramètres signifie :

1) déterminer à quelles valeurs de paramètres des solutions existent ;

2) pour chaque système admissible de valeurs de paramètres, trouver l'ensemble de solutions correspondant.

Une équation avec un paramètre peut être résolue par les méthodes suivantes : analytique ou graphique.

Méthode analytique assume la tâche d'étudier l'équation en considérant plusieurs cas, dont aucun ne peut être manqué.

La solution de l'équation et de l'inégalité avec des paramètres de chaque type par la méthode analytique implique une analyse détaillée de la situation et une étude cohérente, au cours de laquelle le besoin s'en fait sentir "manipulation douce" avec paramètre.

Méthode graphique implique la construction d'un graphique de l'équation, grâce auquel il est possible de déterminer comment, respectivement, le changement du paramètre affecte la solution de l'équation. Le graphique permet parfois de formuler analytiquement les conditions nécessaires et suffisantes pour résoudre les tâches définies. La méthode de résolution graphique est particulièrement efficace lorsqu'il est nécessaire d'établir le nombre de racines de l'équation en fonction du paramètre et présente l'avantage incontestable de le voir visuellement.

§ 1. Équations linéaires et inégalités.

Équation linéaire UN X = b , écrit sous forme générale, peut être considéré comme une équation à paramètres, où X - inconnu , un , b - options. Pour cette équation, la valeur spéciale ou de contrôle du paramètre est celle à laquelle le coefficient disparaît dans l'inconnue.

Lors de la résolution d'une équation linéaire avec un paramètre, les cas sont pris en compte lorsque le paramètre est égal à sa valeur spéciale et différent de celle-ci.

Valeur du paramètre spécial un est la valeur UN = 0.

b = 0 est une valeur de paramètre spécial b .

À b ¹ 0 l'équation n'a pas de solutions.

À b = 0 l'équation prendra la forme : 0x = 0. La solution de cette équation est n’importe quel nombre réel.

Inégalités de forme ah > b Et hache < b (une ≠ 0) sont appelées inégalités linéaires. Ensemble de solutions aux inégalités ah >b– intervalle

(; +), Si un > 0 , Et (-;) , Si UN< 0 . De même pour l'inégalité

Oh< b ensemble de solutions - intervalle(-;), Si un > 0, Et (; +), Si UN< 0.

Exemple 1. Résous l'équation hache = 5

Solution: Il s’agit d’une équation linéaire.

Si une = 0, alors l'équation 0 × x = 5 n'a pas de solution.

Si UN¹ 0, x =- solution de l'équation.

Répondre: à UN¹ 0,x=

pour a = 0 il n’y a pas de solution.

Exemple 2. Résous l'équation hache – 6 = 2a – 3x.

Solution: C'est une équation linéaire, hache – 6 = 2a – 3x (1)

hache + 3x = 2a +6

Réécrire l'équation comme (une+3)x = 2(une+3), considérons deux cas :

une= -3 Et UN¹ -3.

Si une= -3, alors n'importe quel nombre réel X est la racine de l’équation (1). Si UN¹ -3 , l'équation (1) a une seule racine x = 2.

Répondre:À une = -3, x R. ; à UN ¹ -3, x = 2.

Exemple 3. À quelles valeurs de paramètre UN parmi les racines de l'équation

2ah – 4kh – une 2 + 4a – 4 = 0 il y a plus de racines 1 ?

Solution: Résolvons l'équation 2ah – 4kh – une 2 + 4a – 4 = 0- équation linéaire

2(une - 2) x = une 2 – 4une +4

2(une - 2) x = (une – 2) 2

À une = 2 résoudre l'équation 0x = 0 sera n’importe quel nombre, y compris un supérieur à 1.

À UN¹ 2x =
. Par condition x > 1, c'est
>1 et >4.

Répondre:À UN (2) U (4;∞).

Exemple 4 . Pour chaque valeur de paramètre UN trouver le nombre de racines de l'équation ah=8.

Solution. hache = 8- équation linéaire.

oui = un– famille de lignes horizontales ;

oui = - Le graphique est une hyperbole. Construisons des graphiques de ces fonctions.

Réponse : Si une =0, alors l'équation n'a pas de solutions. Si une ≠ 0, alors l'équation a une solution.

Exemple 5 . À l'aide de graphiques, découvrez combien de racines l'équation possède :

|x| = ah – 1.

y =| X | ,

oui = ah – 1– le graphique est une droite passant par un point (0;-1).

Construisons des graphiques de ces fonctions.

Réponse : Quand |a|>1- une racine

à | un|≤1 – l'équation n'a pas de racines.

Exemple 6 . Résoudre les inégalités hache + 4 > 2x + a 2

Solution : hache + 4 > 2x + a 2
(une – 2) x >UN 2 – 4. Considérons trois cas.

Répondre. x > une + 2à une > 2 ; X<а + 2, à UN< 2; à une=2 il n'y a pas de solutions.

§2. Équations quadratiques et inégalités

Équation quadratique est une équation de la forme Oh ² + b x + c = 0 , Où une≠ 0,

UN, b , Avec - options.

Pour résoudre des équations quadratiques avec un paramètre, vous pouvez utiliser les méthodes de résolution standard à l'aide des formules suivantes :

1 ) discriminant d'une équation quadratique : D = b ²-4 ca , (
²- ac)

2) formules pour les racines d'une équation quadratique :X 1 =
, X 2 =
,

(X 1,2 =
)

Les inégalités quadratiques sont appelées

un X 2 + b x + c > 0,un X 2 + b x + c< 0, (1), (2)

un X 2 + b x + c ≥ 0,un X 2 + b x + c ≤ 0,(3), (4)

L'ensemble des solutions à l'inégalité (3) est obtenu en combinant les ensembles de solutions à l'inégalité (1) et l'équation , un X 2 + b x + c = 0. L’ensemble des solutions aux inégalités (4) peut être trouvé de la même manière.

Si le discriminant d'un trinôme quadratique un X 2 + b x + c est inférieur à zéro, alors pour a > 0 le trinôme est positif pour tout x R..

Si un trinôme quadratique a des racines (x 1 < х 2 ), alors pour a > 0 il est positif sur l'ensemble(-; x2 )
(X 2; +) et négatif sur l'intervalle

(x1;x2 ). Si un< 0, то трехчлен положителен на интервале (х 1 ; x2 ) et négatif pour tout x (-; x1 )
(X 2; +).

Exemple 1. Résous l'équation ax² - 2 (a – 1)x – 4 = 0.

C'est une équation quadratique

Solution: Sens spécial une = 0.

À une = 0 on obtient une équation linéaire 2x – 4 = 0. Il a une seule racine x = 2.

À une ≠ 0. Trouvons le discriminant.

D = (a-1)² + 4a = (a+1)²

Si une = -1, Que D = 0 - une racine.

Trouvons la racine en remplaçant une = -1.

-x² + 4x – 4= 0, c'est x² -4x + 4 = 0, nous trouvons que x=2.

Si une ≠ - 1, Que D >0 . En utilisant la formule racine, nous obtenons :x=
;

X 1 =2,x 2 = -.

Répondre:À a=0 et a= -1 l'équation a une racine x = 2 ;à une ≠ 0 et

UN ≠ - 1 équation a deux racinesX 1 =2,x 2 =-.

Exemple 2. Trouver le nombre de racines de cette équation x²-2x-8-a=0 en fonction des valeurs des paramètres UN.

Solution. Réécrivons cette équation sous la forme x²-2x-8=une

oui = x²-2x-8- le graphique est une parabole ;

oui =un- une famille de lignes horizontales.

Construisons des graphiques de fonctions.

Réponse : Quand UN<-9 , l'équation n'a pas de solutions ; lorsque a=-9, l'équation a une solution ; à a>-9, l'équation a deux solutions.

Exemple 3. À quoi UN inégalité (une – 3) x 2 – 2ax + 3a – 6 >0 est valable pour toutes les valeurs de x ?

Solution. Un trinôme quadratique est positif pour toutes les valeurs de x si

a-3 > 0 et D<0, т.е. при а, удовлетворяющих системе неравенств

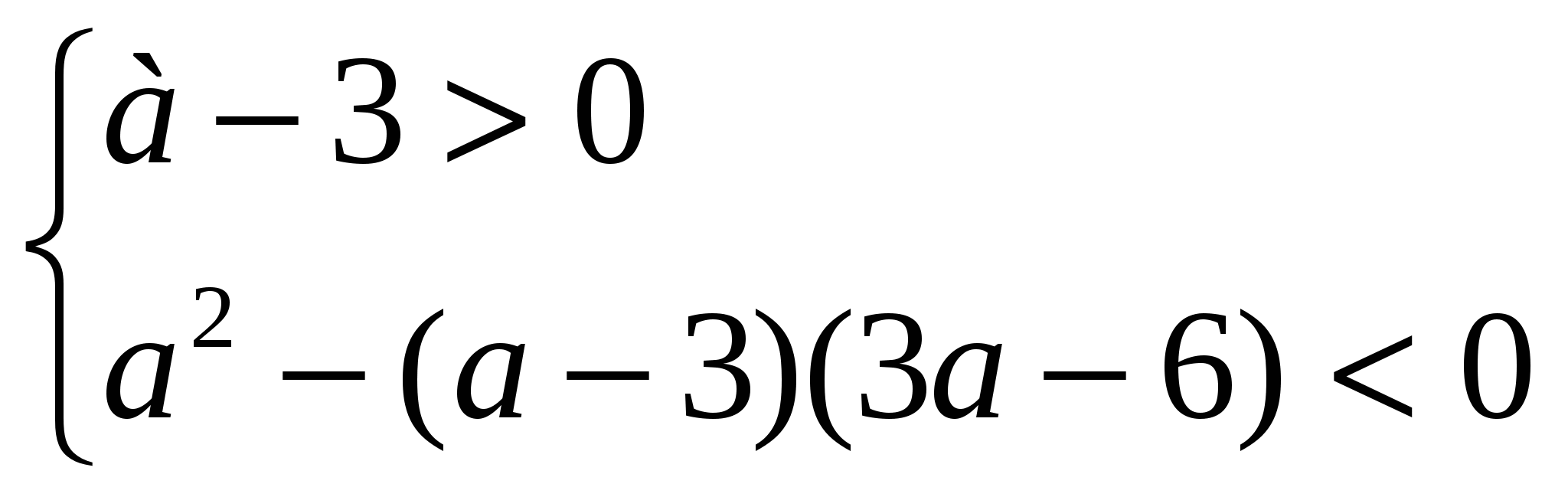
, d'où il s'ensuit queun > 6 .

Répondre.un > 6

§3. Equations rationnelles fractionnaires avec paramètre,

réductible à linéaire

Le processus de résolution d'équations fractionnaires s'effectue selon le schéma habituel : le fractionnaire est remplacé par un nombre entier en multipliant les deux parties de l'équation par le dénominateur commun de ses parties gauche et droite. Après cela, toute l'équation est résolue, à l'exclusion des racines superflues, c'est-à-dire des nombres qui ramènent le dénominateur à zéro.

Dans le cas des équations à paramètre, ce problème est plus complexe. Ici, afin de « éliminer » les racines superflues, il est nécessaire de trouver la valeur du paramètre qui ramène le dénominateur commun à zéro, c'est-à-dire de résoudre les équations correspondantes pour le paramètre.

Exemple 1. Résous l'équation
= 0

Solution: D.Z : x +2 ≠ 0, x ≠ -2

x – une = 0, x = une.

Répondre:À une ≠ - 2, x=une

À une = -2 il n'y a pas de racines.

Exemple 2 . Résous l'équation
-
=
(1)

Ceci est une équation rationnelle fractionnaire

Solution: Signification une = 0 est spécial. À une = 0 l'équation n'a aucun sens et n'a donc pas de racines. Si une ≠ 0, puis après transformations l'équation prendra la forme : x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- équation quadratique.

Trouvons le discriminant = (1 – a)² - (a² – 2a – 3)= 4, trouver les racines de l'équationX 1 = une + 1, x 2 = un - 3.

En passant de l'équation (1) à l'équation (2), le domaine de définition de l'équation (1) s'est élargi, ce qui pourrait conduire à l'apparition de racines superflues. Une vérification est donc nécessaire.

Examen. Excluons des valeurs trouvées X ceux dans lesquels

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

Si X 1 +1=0, c'est (une+1) + 1= 0, Que une= -2. Ainsi,

à une= -2 , X 1 -

Si X 1 +2=0, c'est (une+1)+2=0, Que une = - 3. Ainsi, quand une = - 3, x 1 - racine étrangère de l’équation. (1).

Si X 2 +1=0, c'est (une – 3) + 1= 0, Que une = 2. Ainsi, quand une = 2x 2 - racine étrangère de l’équation (1).

Si X 2 +2=0, c'est ( une – 3) + 2 = 0, Que une=1. Ainsi, quand une = 1,

X 2 - racine étrangère de l'équation (1).

Conformément à cela, lorsque une = - 3 on a x = - 3 – 3 = -6;

à une = - 2 x = -2 – 3= - 5;

à une = 1 x =1 + 1= 2 ;

à une = 2x = 2+1 = 3.

Vous pouvez écrire la réponse.

Répondre: 1) si une= -3, Que x= -6 ; 2) si une= -2, Que x= -5; 3) si une = 0, alors il n'y a pas de racines ; 4) si une= 1, Que x=2 ; 5) si une=2, Que x=3; 6) si une ≠ -3, une ≠ -2, une ≠ 0, une≠ 1, une ≠ 2, puis x 1 = une + 1, x 2 = a-3.

§4. Équations irrationnelles et inégalités

Les équations et inégalités dans lesquelles la variable est contenue sous le signe racine sont appelées irrationnel.

Résoudre des équations irrationnelles revient à passer d'une équation irrationnelle à une équation rationnelle en exposant les deux côtés de l'équation ou en remplaçant une variable. Lorsque les deux côtés de l’équation sont élevés à une puissance égale, des racines étrangères peuvent apparaître. Par conséquent, lorsque vous utilisez cette méthode, vous devez vérifier toutes les racines trouvées en les remplaçant dans l'équation d'origine, en tenant compte des changements dans les valeurs des paramètres.

Tapez l'équation
=g (x) est équivalent au système

L'inégalité f (x) ≥ 0 découle de l'équation f (x) = g 2 (x).

Lors de la résolution d'inégalités irrationnelles, nous utiliserons les transformations équivalentes suivantes :

≤ g(x)


≥g(x)

Exemple 1. Résous l'équation
= x + 1 (3)

C'est une équation irrationnelle

Solution: Par définition d'une racine arithmétique, l'équation (3) est équivalente au système
.

À une = 2 la première équation du système a la forme 0 x = 5, c'est-à-dire qu'il n'a pas de solutions.

À une≠ 2x=
. Découvrons à quelles valeursUN valeur trouvéeX satisfait l'inégalitéx ≥ -1 :
≥ - 1,
≥ 0,

où une ≤ ou une > 2.

Répondre:À une≤, une > 2 x=
, à < а ≤ 2 l'équation n'a pas de solutions.

Exemple 2. Résous l'équation
= un (Annexe 4)

Solution. oui =

oui = un– une famille de lignes horizontales.

Construisons des graphiques de fonctions.

Répondre: à UN<0 – il n'y a pas de solutions ;

à UN≥ 0 - une solution.

Exemple 3 . Résolvons les inégalités(a+1)
<1.

Solution. O.D.Z. x ≤ 2. Si a+1 ≤0, alors l'inégalité est vraie pour toutes les valeurs admissibles X. Si a+1>0, Que

(a+1)
<1.

<

où X (2-
2

Répondre. X (- ;2à (-;-1, X (2-
2

à UN (-1;+).

§ 5. Équations trigonométriques et inégalités.

Voici les formules pour résoudre les équations trigonométriques les plus simples :

Sinx = un
x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = une
x = ±arccos a + 2 πn, n Z, ≤1. (2)

Si >1, alors les équations (1) et (2) n’ont pas de solutions.

bronzage x = une
x= arctan a + πn, n Z, une R.

ctg x = a
x = arcctg a + πn, n Z, une R.

Pour chaque inégalité type nous indiquons l’ensemble des solutions :

1. péché x > a
arcsin a + 2 πn Z,

à un <-1, X R. ; à un ≥ 1, il n'y a pas de solutions.

2. . péché x< a
π - arcsin a + 2 πnZ,

pour a≤-1, il n’y a pas de solutions ; pour un > 1,X R.

3. parce que X > un
- arccos un + 2 πn < X < arccos un + 2 πn , n Z ,

à UN<-1, X R. ; à un ≥ 1 , il n'y a pas de solutions.

4. parce que x arccos a+ 2 πnZ,

à a≤-1 , aucune solution ; àun > 1, X R.

5. tan x > a, arctan a + πnZ

6.tgx< a, -π/2 + πn Z

Exemple 1. Trouver UN, pour laquelle cette équation a une solution :

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Solution.Écrivons l'équation sous la forme

Avecsystème d'exploitation 2 X + (2 un -4) cosx +(un – 5)(a+1) =0, en le résolvant comme une quadratique, nous obtenons cosx = 5-UN Et cosx = -a-1.

L'équation cosx = 5- UN a des solutions fournies -1≤ 5-UN ≤1
4≤ UN≤ 6, et l'équation. cosx = - a-1 à condition -1≤ -1-UN ≤ 1
-2 ≤ UN ≤0.

Répondre. UN -2; 0
4; 6

Exemple 2. À quoi bil y a telle que l'inégalité
+ b> 0 est valable pour tout x ≠πn , n Z .

Solution. Mettons UN= 0. L’inégalité est vraie pour b >0. Montrons maintenant qu'aucun b ≤0 ne satisfait les conditions du problème. En effet, il suffit de mettre x = π /2, Si UN <0, и х = - π /2 à UN ≥0.

Répondre.b>0

§ 6. Équations exponentielles et inégalités

1. Équation h(X) F ( X ) = h(X) g ( X) à h(X) > 0 équivaut à une collection de deux systèmes
Et

2. Dans le cas particulier (h (x)= un ) l'équation UN f(x) = UN g(x) à UN> 0, équivaut à une collection de deux systèmes

Et

3. Équation UN f(x) = b , Où UN > 0, un ≠1, b>0, équivalent à l'équation

f (x )= log a b . Événement UN=1 sont considérés séparément.

La solution aux inégalités exponentielles les plus simples repose sur la propriété de puissance. Inégalité de formeF(un X ) > 0 en utilisant le changement de variablet= un X se réduit à résoudre le système d’inégalités
puis à résoudre les inégalités exponentielles simples correspondantes.

Lors de la résolution d’une inégalité non stricte, il est nécessaire d’ajouter les racines de l’équation correspondante à l’ensemble des solutions de l’inégalité stricte. Comme pour résoudre des équations dans tous les exemples contenant l'expression UN f (x), nous supposons UN> 0. Cas UN= 1 sont considérés séparément.

Exemple 1 . À quoi UNéquation 8 x =
n'a que des racines positives ?

Solution. Par la propriété d'une fonction exponentielle de base supérieure à un, on a x>0
8 X >1

>1

>0, d'oùun (1,5;4).

Répondre. un (1,5;4).

Exemple 2. Résoudre les inégalités un 2 ∙2 X > un

Solution. Considérons trois cas :

1. UN< 0 . Puisque le côté gauche de l’inégalité est positif et le côté droit est négatif, l’inégalité est valable pour tout x R..

2. un=0. Il n'y a pas de solutions.

3. UN > 0 . un 2 ∙2 X > un
2 X >
x > -log 2 un

Répondre. X R.à UN > 0 ; il n'y a pas de solutions pour un =0; X (- enregistrer 2 un; +) àune> 0 .

§ 7. Équations logarithmiques et inégalités

Présentons quelques équivalences utilisées pour résoudre équations logarithmiques et inégalités.

1. L'équation log f (x) g (x) = log f (x) h (x) est équivalente au système

En particulier, si UN >0, UN≠1, alors

enregistrer un g(x)=log un h(x)

2. L'équation enregistrer un g(x)=b
g(x)=un b ( UN >0, une ≠ 1, g(x) >0).

3. Inégalité enregistrer F ( X ) g (X) ≤ enregistrer F ( X ) h(X) équivaut à une combinaison de deux systèmes :
Et

Si un, b sont des nombres, a >0, a ≠1, alors

enregistrer un f(x) ≤b

enregistrer un f(x)>b

Exemple 1. Résous l'équation

Solution. Trouvons l'ODZ : x > 0, x ≠ UN 4 , un > 0, UN≠ 1. Transformer l'équation

enregistrer x – 2 = 4 – enregistrer un X
enregistrer x + enregistrer un X– 6 = 0, d'où enregistrer un X = - 3

X = UN-3 et enregistrer un X = 2
X = UN 2. Condition x = UN 4
UN – 3 = UN 4 ou UN 2 = UN 4 n’est pas effectué sur ODZ.

Répondre: X = UN-3, x = UN 2 à UN (0; 1)
(1; ).

Exemple 2 . Trouvez la plus grande valeur UN, pour lequel l'équation

2 enregistrer -
+ un = 0 a des solutions.

Solution. Nous ferons un remplacement
= tet nous obtenons l'équation quadratique 2t 2 – t + un = 0. En résolvant, on trouveD = 1-8 un . Considérons D≥0, 1-8 UN ≥0
UN ≤.

À UN = l'équation quadratique a une racinet= >0.

Répondre. UN =

Exemple 3 . Résoudre les inégalitésenregistrer(X 2 – 2 X + un ) > - 3

Solution. Résolvons le système d'inégalités

Racines des trinômes carrés x 1,2 = 1 ±
leur 3,4 = 1 ±
.

Valeurs des paramètres critiques : UN= 1 et UN= 9.

Soient X 1 et X 2 les ensembles de solutions aux première et deuxième inégalités, alors

X1
X 2 = X – solution à l'inégalité d'origine.

À 0< un <1 Х 1 = (- ;1 -
)
(1 +
; +), àUN> 1X1 = (-;+).

À 0< un < 9 Х 2 = (1 -
; 1 +
), àUN≥9 X 2 – aucune solution.

Considérons trois cas :

1. 0< un ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < un < 9 Х = (1 -
;1 +
).

3. un≥ 9 X – aucune solution.

Objectifs de l'examen d'État unifié

Haut niveau C1, C2

Exemple 1. Trouver toutes les valeurs R., pour lequel l'équation

R. ∙ ctg2x+2sinx+ p= 3 a au moins une racine.

Solution. Transformons l'équation

R. ∙ (
- 1) + 2sinx + p= 3, sinx =t, t
,t 0.

- p+2t+ p = 3, + 2t = 3, 3 -2t = , 3t 2 – 2t 3 = p .

Laisser F(oui) = 3 t 2 – 2 t 3 . Trouvons l'ensemble des valeurs de fonctionF(X) sur


. à / = 6 t – 6 t 2 , 6 t - 6 t 2 = 0, t 1 =0, t 2 = 1. F(-1) = 5, F(1) = 1.

À t
, E(F) =
,

À t
, E(F) =
, c'est quand t


, E(F) =
.

À l'équation 3t 2 – 2 t 3 = p (d'où ce qui est donné) avait au moins une racine nécessaire et suffisantep E(F), c'est p
.

Répondre.
.

Exemple 2.

À quelles valeurs de paramètreUN l'équation enregistrer
(4 X 2 – 4 un + un 2 +7) = 2 a exactement une racine ?

Solution. Transformons l'équation en une équation équivalente à celle-ci :

4x2 – 4 un + un 2 +7 = (x2 + 2) 2.

Notez que si un certain nombre x est la racine de l’équation résultante, alors le nombre – x est également la racine de cette équation. Par condition, cela n’est pas réalisable, donc la seule racine est le nombre 0.

Nous trouverons UN.

4∙ 0 2 - 4un + un 2 +7 = (0 2 + 2) 2 ,

un 2 - 4un +7 = 4, un 2 - 4un +3 = 0, un 1 = 1, un 2 = 3.

Examen.

1) un 1 = 1. L’équation ressemble alors à :enregistrer
(4 X 2 +4) =2. Résolvons-le

4x 2 + 4 = (x 2 + 2) 2, 4x 2 + 4 = x 4 + 4x 2 + 4, x 4 = 0, x = 0 est la seule racine.

2) un 2 = 3. L'équation ressemble à :enregistrer
(4 X 2 +4) =2
x = 0 est la seule racine.

Répondre. 1; 3

Haut niveau C4, C5

Exemple 3. Trouver toutes les valeurs R, pour laquelle l'équation

x2 – ( R.+ 3)x + 1= 0 a des racines entières et ces racines sont des solutions à l'inégalité : x 3 - 7 R. x2 + 2x2 – 14 R. x-3x +21 R. ≤ 0.

Solution. Soit x 1, X 2 – racines entières de l'équation x 2 – (R. + 3)x + 1= 0. Alors, par la formule de Vieta, x 1 +x 2 = R. + 3,x 1 ∙x 2 = 1. Le produit de deux entiers x 1 , X 2 peut être égal à un seulement dans deux cas : x 1 =x 2 = 1 ou x 1 =x 2 = - 1. Si x 1 =x 2 = 1, alorsR. + 3 = 1+1 = 2
R. = - 1 ; si x 1 =x 2 = - 1, alorsR. + 3 = - 1 – 1 = - 2
R. = - 5. Vérifiez si les racines de l'équation x 2 – (R. + 3)x + 1= 0 dans les cas décrits par solutions à cette inégalité. Pour l'occasionR. = - 1,x 1 =x 2 = 1 nous avons

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – vrai ; pour l'occasion R.= - 5, x 1 = x 2 = - 1 nous avons (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 – correct. Ainsi, les conditions du problème ne sont satisfaites que R.= - 1 et R. = - 5.

Répondre.R. 1 = - 1 et R. 2 = - 5.

Exemple 4. Trouver toutes les valeurs positives du paramètre UN, pour lequel le nombre 1 appartient au domaine de définition de la fonction

à = (UN
- UN
).

Type d'emploi : 18

Condition

Pour quelles valeurs du paramètre a l'inégalité est-elle

\log_(5)(4+a+(1+5a^(2)-\cos^(2)x) \cdot\sin x - a \cos 2x) \leq 1 est satisfait pour toutes les valeurs de x ?

Afficher la solution

Solution

Cette inégalité équivaut à la double inégalité 0 < 4+a+(5a^{2}+\sin^{2}x) \sin x+ une(2 \sin^(2)x-1) \leq 5 .

Soit \sin x=t , alors on obtient l'inégalité :

4 < t^{3}+2at^{2}+5a^{2}t \leq 1 \: (*) , qui doit être exécuté pour toutes les valeurs de -1 \leq t \leq 1 . Si a=0, alors l'inégalité (*) est valable pour tout t\in [-1;1] .

Soit a \neq 0 . La fonction f(t)=t^(3)+2at^(2)+5a^(2)t augmente sur l'intervalle [-1;1] , puisque la dérivée f"(t)=3t^(2) +4at +5a^(2) > 0 pour toutes les valeurs de t \in \mathbb(R) et a \neq 0 (discriminant D< 0 и старший коэффициент больше нуля).

L'inégalité (*) sera satisfaite pour t \in [-1;1] dans les conditions

\begin(cases) f(-1) > -4, \\ f(1) \leq 1, \\ a \neq 0; \fin(cas)\ : \Leftrightarrow \begin(cases) -1+2a-5a^(2) > -4, \\ 1+2a+5a^(2) \leq 1, \\ a \neq 0; \fin(cas)\ : \Leftrightarrow \begin(cases) 5a^(2)-2a-3< 0, \\ 5a^{2}+2a \leq 0, \\ a \neq 0; \end{cases}\: \Leftrightarrow -\frac(2)(5)\leq a< 0 .

Ainsi, la condition est satisfaite lorsque -\frac(2)(5) \leq a \leq 0 .

Répondre

\left [ -\frac(2)(5); 0\droite]

Source : « Mathématiques. Préparation à l'examen d'État unifié 2016. Niveau profil." Éd. F. F. Lysenko, S. Yu. Kulabukhova.

Type d'emploi : 18
Sujet : Inégalités avec un paramètre

Condition

Trouver toutes les valeurs du paramètre a , pour chacune desquelles l'inégalité

x^2+3|x-a|-7x\leqslant -2a

a une solution unique.

Afficher la solution

Solution

L'inégalité équivaut à un ensemble de systèmes d'inégalités

\left[\!\!\begin(array)(l) \begin(cases) x \geqslant a, \\ x^2+3x-3a-7x+2a\leqslant0; \fin(cas) \\ \begin(cas)x \left[\!\!\begin(array)(l) \begin(cases) x \geqslant a, \\ x^2-4x-a\leqslant0; \fin(cas) \\ \begin(cas)x \left[\!\!\begin(array)(l) \begin(cases) a \leqslant x, \\ a\geqslant x^2-4x; \end(cases) \\ \begin(cases)a>x, \\ a\leqslant -\frac(x^2)(5)+2x. \end(cases)\end(array)\right.

Dans le système de coordonnées Oxa, nous construirons des graphiques de fonctions a=x, a=x^2-4x, a=-\frac(x^2)(5)+2x.

L'ensemble résultant est satisfait par les points compris entre les graphiques des fonctions a=x^2-4x, a=-\frac(x^2)(5)+2x sur l'intervalle x\in (zone ombrée).

À partir du graphique, nous déterminons : l’inégalité originale a une solution unique pour a=-4 et a=5, puisque dans la zone ombrée il y aura un seul point d’ordonnée a égale à -4 et égale à 5.

Travaux de cours

Interprète : Bugrov S K.

L'étude de nombreux processus physiques et motifs géométriques conduit souvent à résoudre des problèmes liés aux paramètres. Certaines universités incluent également des équations, des inégalités et leurs systèmes dans les épreuves d'examen, qui sont souvent très complexes et nécessitent une approche de solution non standard. À l'école, cette section, l'une des plus difficiles du cours de mathématiques, n'est abordée que dans quelques cours au choix.

En préparant ce travail, je me suis fixé pour objectif une étude plus approfondie de ce sujet, en identifiant la solution la plus rationnelle qui mène rapidement à une réponse. À mon avis, la méthode graphique est un moyen pratique et rapide de résoudre des équations et des inégalités avec paramètres.

Mon essai traite des types d'équations fréquemment rencontrés, des inégalités et de leurs systèmes, et j'espère que les connaissances que j'ai acquises au cours du travail m'aideront lors de la réussite des examens scolaires et lors de l'entrée à l'université.

§ 1. Définitions de base

Considérons l'équation

¦(une, b, c, …, k, x)=j(une, b, c, …, k, x), (1)

où a, b, c, …, k, x sont des quantités variables.

Tout système de valeurs variables

a = a0, b = b0, c = c0, …, k = k0, x = x0,

sous lequel les parties gauche et droite de cette équation prennent des valeurs réelles, est appelé le système de valeurs admissibles des variables a, b, c, ..., k, x. Soit A l'ensemble de toutes les valeurs admissibles de a, B l'ensemble de toutes les valeurs admissibles de b, etc., X l'ensemble de toutes les valeurs admissibles de x, c'est-à-dire аОА, bОB, …, xОX. Si chacun des ensembles A, B, C, …, K choisit et fixe, respectivement, une valeur a, b, c, …, k et les substitue dans l'équation (1), alors nous obtenons une équation pour x, c'est-à-dire équation à une inconnue.

Les variables a, b, c, ..., k, qui sont considérées comme constantes lors de la résolution de l'équation, sont appelées paramètres, et l'équation elle-même est appelée une équation contenant des paramètres.

Les paramètres sont désignés par les premières lettres de l'alphabet latin : a, b, c, d, …, k, l, m, n, et les inconnus par les lettres x, y, z.

Résoudre une équation avec des paramètres signifie indiquer à quelles valeurs des paramètres des solutions existent et quelles sont elles.

Deux équations contenant les mêmes paramètres sont dites équivalentes si :

a) ils ont un sens pour les mêmes valeurs de paramètres ;

b) toute solution de la première équation est une solution de la seconde et vice versa.

§ 2. Algorithme de solution.

Trouvez le domaine de définition de l'équation.

On exprime a en fonction de x.

Dans le système de coordonnées xOa, nous construisons un graphique de la fonction a=¦(x) pour les valeurs de x qui sont incluses dans le domaine de définition de cette équation.

On trouve les points d'intersection de la droite a=c, où cÎ(-¥;+¥) avec le graphe de la fonction a=¦(x). Si la droite a=c coupe le graphe a=¦(x) , puis on détermine l'abscisse des points d'intersection. Pour ce faire, il suffit de résoudre l’équation a=¦(x) pour x.

Nous écrivons la réponse.

I. Résoudre l'équation

(1)

Puisque x=0 n’est pas une racine de l’équation, l’équation peut être résolue pour a :

ou

Le graphique d’une fonction est constitué de deux hyperboles « collées ». Le nombre de solutions à l'équation originale est déterminé par le nombre de points d'intersection de la ligne construite et de la droite y=a.

Si un О (-¥;-1]П(1;+¥)П

, alors la droite y=a coupe le graphique de l'équation (1) en un point. Nous trouverons l'abscisse de ce point lors de la résolution de l'équation de x.

Ainsi, sur cet intervalle, l'équation (1) a une solution

. , alors la droite y=a coupe le graphique de l'équation (1) en deux points. Les abscisses de ces points peuvent être trouvées à partir des équations et , on obtient et . , alors la droite y=a ne coupe pas le graphique de l'équation (1), donc il n'y a pas de solutions.

Si un О (-¥;-1]П(1;+¥)П

, Que ; , Que , ; , alors il n'y a pas de solutions.

II. Trouver toutes les valeurs du paramètre a pour lesquelles l'équation

a trois racines différentes.

Réécrire l'équation comme

et après avoir examiné une paire de fonctions, vous remarquerez que les valeurs souhaitées du paramètre a et elles seules correspondront aux positions du graphique de la fonction auxquelles il a exactement trois points d'intersection avec le graphique de la fonction .

Dans le système de coordonnées xOy nous allons construire un graphique de la fonction

). Pour ce faire, nous pouvons la représenter sous la forme et, après avoir considéré quatre cas qui se présentent, nous écrivons cette fonction sous la forme

Depuis le graphique de la fonction

- il s'agit d'une droite ayant un angle d'inclinaison par rapport à l'axe Ox égal à , et coupant l'axe Oy en un point de coordonnées (0, a), on conclut que les trois points d'intersection indiqués ne peuvent être obtenus que dans le cas où cette ligne touche le graphique de la fonction. On trouve donc la dérivée.

III. Trouver toutes les valeurs du paramètre a, pour chacune desquelles le système d'équations

a des solutions.

De la première équation du système on obtient

Par conséquent, cette équation définit une famille de « semi-paraboles » - les branches droites de la parabole « glissent » avec leurs sommets le long de l'axe des abscisses.

Sélectionnons les carrés complets du côté gauche de la deuxième équation et factorisons-la

De nombreux points de l'avion

satisfaisant la deuxième équation sont deux droites et

Voyons à quelles valeurs du paramètre a une courbe de la famille des « semiparaboles » a au moins un point commun avec l'une des droites résultantes.

Résoudre des inégalités avec un paramètre.

Inégalités qui ont la forme ax > b, ax< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются inégalités linéaires.

Les principes de résolution d'inégalités linéaires avec un paramètre sont très similaires aux principes de résolution d'équations linéaires avec un paramètre.

Exemple 1.

Résolvez l'inégalité 5x – a > hache + 3.

Solution.

Tout d’abord, transformons l’inégalité d’origine :

5x – ax > a + 3, retirons x des parenthèses du côté gauche de l’inégalité :

(5 – a)x > a + 3. Considérons maintenant les cas possibles pour le paramètre a :

Si a > 5, alors x< (а + 3) / (5 – а).

Si a = 5, alors il n’y a pas de solutions.

Si un< 5, то x >(une + 3) / (5 – une).

Cette solution sera la réponse à l’inégalité.

Exemple 2.

Résoudre l'inégalité x(a – 2) / (a ​​​​- 1) – 2a/3 ≤ 2x – a pour a ≠ 1.

Solution.

Transformons l'inégalité originelle :

x(une – 2) / (une ​​​​– 1) – 2x ≤ 2une/3 – une;

Ах/(а – 1) ≤ -а/3. En multipliant les deux côtés de l’inégalité par (-1), on obtient :

hache/(une – 1) ≥ une/3. Explorons les cas possibles pour le paramètre a :

1 cas. Soit a/(a – 1) > 0 ou a € (-∞; 0)ᴗ(1; +∞). Alors x ≥ (a – 1)/3.

Cas 2. Soit a/(a – 1) = 0, c'est-à-dire a = 0. Alors x est n'importe quel nombre réel.

Cas 3. Soit a/(a – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Réponse : x € [(a – 1)/3 ; +∞) pour un € (-∞ ; 0)ᴗ(1 ; +∞) ;
x € [-∞ ; (a – 1)/3] pour un € (0 ; 1) ;
x € R pour a = 0.

Exemple 3.

Résoudre l'inégalité |1 + x| ≤ hache par rapport à x.

Solution.

Il découle de la condition que le membre droit de l'axe des inégalités doit être non négatif, c'est-à-dire ax ≥ 0. Par la règle de révélation du module de l'inégalité |1 + x| ≤ hache on a une double inégalité

Hache ≤ 1 + x ≤ hache. Réécrivons le résultat sous la forme d'un système :

(hache ≥ 1 + x ;
(-ax ≤ 1 + x.

Transformons-le en :

((une – 1)x ≥ 1 ;
((une + 1)x ≥ -1.

Nous étudions le système résultant sur les intervalles et aux points (Fig. 1):

Pour a ≤ -1 x € (-∞; 1/(a – 1)].

À 1< а < 0 x € [-1/(а – 1); 1/(а – 1)].

Quand a = 0 x = -1.

À 0< а ≤ 1 решений нет.

Méthode graphique pour résoudre les inégalités

Le traçage de graphiques simplifie grandement la résolution d'équations contenant un paramètre. L'utilisation de la méthode graphique pour résoudre des inégalités avec un paramètre est encore plus claire et plus pratique.

Résoudre graphiquement des inégalités de la forme f(x) ≥ g(x) signifie trouver les valeurs de la variable x pour lesquelles le graphique de la fonction f(x) se situe au-dessus du graphique de la fonction g(x). Pour ce faire, il faut toujours trouver les points d'intersection des graphiques (s'ils existent).

Exemple 1.

Résoudre l'inégalité |x + 5|< bx.

Solution.

Nous construisons des graphiques de fonctions y = |x + 5| et y = bx (Fig.2). La solution de l'inégalité sera les valeurs de la variable x pour lesquelles le graphique de la fonction y = |x + 5| sera en dessous du graphique de la fonction y = bx.

L'image montre:

1) Pour b > 1, les droites se coupent. L'abscisse du point d'intersection des graphiques de ces fonctions est la solution de l'équation x + 5 = bx, d'où x = 5/(b – 1). Le graphique y = bx est situé au-dessus en x de l'intervalle (5/(b – 1); +∞), ce qui signifie que cet ensemble est la solution de l'inégalité.

2) De même on trouve qu'à -1< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) Pour b ≤ -1 x € (-∞; 5/(b – 1)).

4) Pour 0 ≤ b ≤ 1, les graphiques ne se coupent pas, ce qui signifie que l'inégalité n'a pas de solution.

Réponse : x € (-∞; 5/(b – 1)) pour b ≤ -1 ;
x € (-5/(b + 1); 5/(b – 1)) à -1< b < 0;
il n'y a pas de solutions pour 0 ≤ b ≤ 1 ; x € (5/(b – 1) ; +∞) pour b > 1.

Exemple 2.

Résolvez l'inégalité a(a + 1)x > (a + 1)(a + 4).

Solution.

1) Trouvons les valeurs « contrôle » du paramètre a : a 1 = 0, et 2 = -1.

2) Résolvons cette inégalité sur chaque sous-ensemble de nombres réels : (-∞; -1) ; (-1); (-dix); (0); (0 ; +∞).

une)une< -1, из данного неравенства следует, что х >(une + 4)/une ;

b) a = -1, alors cette inégalité prendra la forme 0 x > 0 – il n'y a pas de solutions ;

c) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, alors cette inégalité a la forme 0 x > 4 – il n'y a pas de solutions ;

e) a > 0, de cette inégalité il résulte que x > (a + 4)/a.

Exemple 3.

Résoudre l’inégalité |2 – |x||< a – x.

Solution.

Nous construisons un graphique de la fonction y = |2 – |x|| (Fig.3) et considérons tous les cas possibles de localisation de la droite y = -x + a.

Réponse : l'inégalité n'a pas de solution pour a ≤ -2 ;
x € (-∞ ; (a – 2)/2) pour un € (-2 ; 2] ;
x € (-∞; (a + 2)/2) pour a > 2.

Lors de la résolution de divers problèmes, équations et inégalités avec paramètres, un nombre important de techniques heuristiques sont découvertes, qui peuvent ensuite être appliquées avec succès dans toutes les autres branches des mathématiques.

Les problèmes liés aux paramètres jouent un rôle important dans la formation de la pensée logique et de la culture mathématique. C'est pourquoi, après avoir maîtrisé les méthodes de résolution de problèmes avec des paramètres, vous réussirez à résoudre d'autres problèmes.

Vous avez encore des questions ? Vous ne savez pas comment résoudre les inégalités ?
Pour obtenir l'aide d'un tuteur -.
Le premier cours est gratuit !

blog.site, lors de la copie totale ou partielle du matériel, un lien vers la source originale est requis.

Série « Apprendre à résoudre des problèmes avec des paramètres »

IV. Équations quadratiques et inégalités avec paramètre

IV.1. Concepts de base

Définition. Une fonction de la forme (1), où , , sont les fonctions données du paramètre UN, considérée à l'intersection de leurs domaines de définition, sera appelée une fonction quadratique de paramètre UN.

Exemples.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

Définition. Sous-domaine de définition de la fonction quadratique (1) avec paramètre UN nous comprendrons l'ensemble des paires de valeurs X Et UN taper ( X; UN), pour chacun desquels l'expression ne perd pas son sens.

Établissons les domaines de définition des fonctions 1-10.

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

Si le paramètre prend une des valeurs numériques de , alors la fonction (1) prendra la forme d'une des fonctions à coefficients numériques :

; ; ;
; ; ; ,

Où k, b, c- nombres réels.

Faisons attention au fait que pour certaines valeurs du paramètre de, une fonction quadratique avec paramètre prend la forme soit d'une fonction quadratique sans paramètre, soit d'une fonction linéaire.

Puisqu’une fonction quadratique avec un paramètre « génère » le plus souvent une famille de fonctions quadratiques ou linéaires avec des coefficients numériques, alors en parlant de graphiques d'une fonction quadratique avec un paramètre, nous entendrons de nombreux graphes de cette famille.

Définition. UN est appelée une équation de la forme (1) où , , sont ces fonctions du paramètre UN, considérés à l’intersection de leurs domaines de définition.

En particulier, certains des coefficients ou du terme d'origine peuvent être des nombres.

Exemples.

, (1)
, (2)
, (3)
, (4)
. (5)

En utilisant la définition d'une fonction quadratique avec un paramètre, nous pouvons donner la définition suivante d'une équation quadratique avec un paramètre.

Définition. Équation quadratique avec paramètre UN est appelée une équation de la forme , où est une fonction quadratique de paramètre UN.

Si , alors l'équation (1) est quadratique au sens traditionnel, c'est-à-dire second degré.
Si , alors l’équation (1) devient linéaire.

Pour toutes les valeurs de paramètres valides UN, pour lequel et , en utilisant des formules connues, nous obtenons des expressions pour les racines de l'équation (1) en termes de paramètre.

Ces valeurs UN, dans lesquels , doivent être considérés séparément comme des cas particuliers.
Ainsi, par exemple, l'équation (5) prendra la forme , d'où .

IV.2. Équations quadratiques avec paramètre

№1. Résous l'équation.

– équation-conséquence. On a: , .

Dans le système de coordonnées ( aoh) nous complétons la solution. (Fig. 1)

Réponse : 1. Si , alors .

2. Si , alors .

3. Si , alors , .

№2. Trouver la valeur du paramètre UN, dans laquelle l'équation a une seule racine. S'il existe plusieurs valeurs de ce type, notez leur somme dans votre réponse.

Cette équation se réduit à un système équivalent :

Mettons-le sous la forme : et résolvons-le graphiquement dans le système de coordonnées ( xOa). (Fig.2).

L'équation a une racine unique en , et .

№3. Trouver toutes les valeurs X tel que pour toute valeur du paramètre UN, n'appartenant pas à l'intervalle (0 ; 2], l'expression n'est pas égale à l'expression. (USE-2007).

Reformulons le problème : « Trouver toutes les valeurs X tel que pour toute valeur du paramètre l'équation n'a pas de racines. »
Exprimons UNà travers X:

1) Laissez . Alors . L’équation a donc des racines. Cela signifie qu’il ne satisfait pas à la condition.
2) Laissez . Alors . Utilisons le système de coordonnées ( xOa). (Fig. 3).

La condition est satisfaite.

№4. Combien de racines en fonction du paramètre UN il y a une équation ?

Développons le module :

Dans le système de coordonnées ( xOy) construisons un graphique de la fonction

et plusieurs lignes d'un crayon de lignes parallèles données par l'équation. (Fig. 4).

Réponse : 1. Si , alors il n’y a pas de racines.

2. Si , alors une racine.

3. Si , alors il y a deux racines.

IV.3. Inégalités quadratiques avec paramètre

№5. Résoudre l'inégalité .

1 voie.

Prenons cela en compte. Alors la solution à cette inégalité pour tout b.(Fig.5).

Si , alors on passe à l'inégalité dont l'ensemble des solutions sera représenté dans le système de coordonnées ( boîte). (Fig.6).

Photo compatible. 5 et 6.

Et maintenant selon la fig. 7, en le coupant avec des lignes droites verticales, il est facile d'obtenir la réponse.

Réponse : 1. Si , alors .
2. Si , alors .
3. Si , alors

Méthode 2.

Résolvons graphiquement l'inégalité dans le système de coordonnées ( xOb):

. (Fig. 8).

Considérons deux cas.

1) . L'inégalité prendra alors la forme où .
2) , alors .

Le graphique de la fonction et la partie du plan contenant les points dont les coordonnées satisfont à l'inégalité sont présentés à la figure 8.

1. Si , alors .
2. Si , alors . 3. Si , alors .

3 voies.

Présentons maintenant une solution graphique dans le système de coordonnées ( xOy). Pour cela, ouvrez le module :

Considérez la fonction .

Racines d'un trinôme quadratique .

Comparons et .

1) , d'où .

Nous obtenons le total. (Fig.9)

2) , d'où . (Fig. 10).

Alors c'est à dire .

3) , d'où . (Fig. 11).

Alors c'est à dire .

Réponse : 1. Si , alors .

2. Si , alors .
3. Si , alors .

№6. Rechercher toutes les valeurs des paramètres UN, pour laquelle la plus petite valeur de la fonction plus de 2.

Il suffit de retrouver toutes les valeurs du paramètre UN, pour chacun desquels l'inégalité est vraie pour tout . Réécrivons l'inégalité sous la forme ., ;