itthon Saját tapasztalat

Lineáris egyenlőtlenségek megoldása paraméterekkel. Oktatóanyag "Egyenletek és egyenlőtlenségek paraméterekkel"

Állami költségvetési oktatási intézmény

Szamarai régió középfokú általános oktatás

iskola 2. szám im. V. Maskina vasút Művészet. Klyavlino

önkormányzati kerület Klyavlinsky

Samara régió

« Egyenletek

És

egyenlőtlenségek

paraméterekkel"

oktatóanyag

Klyavlino

oktatóanyag

"Egyenletek és egyenlőtlenségek paraméterekkel" osztályos tanulók számára a 10-11

ez a kézikönyv az "Egyenletek és egyenlőtlenségek a paraméterekkel" választható kurzus programjának melléklete, amely külső vizsgán ment (a Szamarai Régió Oktatási és Tudományos Minisztériumának 2008. december 19-i tudományos és módszertani szakértői tanácsát ajánlották a szamarai régió oktatási intézményeiben való használatra)

Szerzői

Romadanova Irina Vladimirovna

Matematika tanár, Klyavlinskaya Középfokú Általános Iskola

2. számú iskola őket. V. Maskina, Klyavlinsky kerület, Szamarai régió

Szerbajeva Irina Alekszejevna

Bevezetés……………………………………………………………… 3-4

Lineáris egyenletek és egyenlőtlenségek paraméterekkel………………..4-7

Másodfokú egyenletek és egyenlőtlenségek paraméterekkel……………7-9

Törtracionális egyenletek paraméterekkel……………..10-11

Irracionális egyenletek és paraméteres egyenlőtlenségek……11-13

Trigonometrikus egyenletek és egyenlőtlenségek paraméterekkel.14-15

Exponenciális egyenletek és egyenlőtlenségek paraméterekkel………16-17

Logaritmikus egyenletek és paraméteres egyenlőtlenségek ...... 16-18

Az egységes államvizsga feladatai…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….

Önálló munkavégzés feladatai………………………………21-28

Bevezetés.

Egyenletek és egyenlőtlenségek paraméterekkel.

Ha egy egyenletben vagy egyenlőtlenségben néhány együtthatót nem adott számértékkel adunk meg, hanem betűkkel jelöljük, akkor ún. paraméterek,és maga az egyenlet vagy egyenlőtlenség parametrikus.

Egy egyenlet vagy egyenlőtlenség paraméterekkel történő megoldásához a következőket kell tennie:

Kiemel különleges jelentése- ez annak a paraméternek az értéke, amelyben vagy áthaladásakor az egyenlet vagy egyenlőtlenség megoldása megváltozik.

Határozza meg megengedett értékek azok a paraméterértékek, amelyeknél az egyenletnek vagy egyenlőtlenségnek van értelme.

Egy egyenlet vagy egyenlőtlenség paraméterekkel való megoldása azt jelenti:

1) határozza meg, hogy a paraméterek milyen értékein léteznek megoldások;

2) minden megengedett paraméterérték-rendszerhez keresse meg a megfelelő megoldáskészletet.

Egy paraméterrel rendelkező egyenlet a következő módszerekkel oldható meg: analitikus vagy grafikus.

Analitikai módszer felvállalja az egyenlet vizsgálatát több olyan eset figyelembevételével, amelyek közül egyet sem lehet kihagyni.

Az egyenlet és egyenlőtlenség megoldása az egyes típusok paramétereivel analitikus módszerrel a helyzet részletes elemzését és következetes vizsgálatát foglalja magában, amely során felmerül az igény "gyengéd kezelés" paraméterrel.

Grafikus módszer magában foglalja az egyenlet grafikonjának felépítését, amellyel meghatározható, hogy a paraméter változása hogyan befolyásolja az egyenlet megoldását. A grafikon olykor lehetővé teszi a kitűzött feladatok megoldásához szükséges és elégséges feltételek analitikus megfogalmazását. A grafikus megoldási módszer különösen akkor hatékony, ha meg kell határozni, hogy az egyenletnek hány gyöke van a paramétertől függően, és kétségtelen előnye, hogy ezt vizuálisan látjuk.

§ 1. Lineáris egyenletek és egyenlőtlenségek.

Lineáris egyenlet A x = b , általános formában írva, paraméteres egyenletnek tekinthető, ahol x – ismeretlen , a , b - lehetőségek. Ennél az egyenletnél a paraméter speciális vagy vezérlőértéke az, amelynél az együttható eltűnik az ismeretlenben.

A lineáris egyenlet paraméterrel történő megoldása során azokat az eseteket vesszük figyelembe, amikor a paraméter megegyezik a speciális értékével és eltér attól.

Speciális paraméterérték a az érték A = 0.

b = 0 egy speciális paraméterérték b .

Nál nél b ¹ 0 az egyenletnek nincsenek megoldásai.

Nál nél b = 0 az egyenlet a következő formában lesz: 0x = 0. Ennek az egyenletnek a megoldása bármely valós szám.

A forma egyenlőtlenségei ah > b És fejsze < b (a ≠ 0) lineáris egyenlőtlenségeknek nevezzük. Az egyenlőtlenség megoldásainak halmaza ah >b– intervallum

(; +), Ha a > 0 , És (-;) , Ha A< 0 . Hasonlóan az egyenlőtlenséghez

Ó< b megoldáskészlet - intervallum(-;), Ha a > 0, És (; +), Ha A< 0.

1. példa oldja meg az egyenletet fejsze = 5

Megoldás: Ez egy lineáris egyenlet.

Ha a = 0, akkor az egyenlet 0 × x = 5 nincs megoldása.

Ha A¹ 0, x =- az egyenlet megoldása.

Válasz: nál nél A¹ 0, x=

a = 0 esetén nincs megoldás.

2. példa oldja meg az egyenletet fejsze - 6 \u003d 2a - 3x.

Megoldás: Ez egy lineáris egyenlet fejsze - 6 \u003d 2a - 3x (1)

ax + 3x = 2a +6

Az egyenlet átírása így (a+3)x = 2(a+3) Nézzünk két esetet:

a= -3És A¹ -3.

Ha a= -3, akkor bármilyen valós szám x az (1) egyenlet gyöke. Ha A¹ -3 , az (1) egyenletnek egyetlen gyöke van x = 2.

Válasz: Nál nél a = -3, x R ; nál nél A ¹ -3, x = 2.

3. példa A paraméter milyen értékeinél A az egyenlet gyökerei között

2x - 4x - a 2 + 4а – 4 = 0 több gyökér van 1 ?

Megoldás: Oldja meg az egyenletet 2x - 4x - a 2 + 4а – 4 = 0- lineáris egyenlet

2 (a - 2) x \u003d a 2 - 4a +4

2(a - 2) x \u003d (a - 2) 2

Nál nél a = 2 az egyenlet megoldása 0x = 0 tetszőleges szám lehet, még 1-nél nagyobb is.

Nál nél A¹ 2 x =
. Feltétel szerint x > 1, vagyis
>1, a > 4.

Válasz: Nál nél A (2) U(4;∞).

4. példa . Minden paraméter értékéhez A keresse meg az egyenlet gyökeinek számát ax=8.

Megoldás. fejsze = 8 egy lineáris egyenlet.

y = a– vízszintes vonalak családja;

y = - a grafikon egy hiperbola. Ezekről a függvényekről grafikonokat készítünk.

Válasz: Ha a = 0, akkor az egyenletnek nincsenek megoldásai. Ha a ≠ 0, akkor az egyenletnek egy megoldása van.

5. példa . Grafikonok segítségével nézze meg, hány gyöke van az egyenletnek:

|x| = fejsze - 1.

y=| x | ,

y = fejsze - 1- a gráf egy ponton áthaladó egyenes (0;-1).

Ezekről a függvényekről grafikonokat készítünk.

Válasz: Mikor |a|>1- egy gyökér

nál nél | a|≤1 Az egyenletnek nincs gyökere.

Példa 6 . Oldja meg az egyenlőtlenséget fejsze + 4 > 2x + a 2

Megoldás : fejsze + 4 > 2x + a 2
(а – 2) х >A 2 – 4. Tekintsünk három esetet.

Válasz. x > a + 2 nál nél a > 2; x<а + 2, nál nél A< 2; nál nél a=2 nincsenek megoldások.

2. §. Másodfokú egyenletek és egyenlőtlenségek

Másodfokú egyenlet a forma egyenlete Ó ² + b x + c = 0 , Ahol a≠ 0,

A, b , Val vel - lehetőségek.

A másodfokú egyenletek paraméterrel történő megoldásához használhatja a szabványos megoldási módszereket a következő képletekkel:

1 ) a másodfokú egyenlet diszkriminánsa: D = b ² - 4 ac , (
²- ac)

2) a másodfokú egyenlet gyökeinek képletei:x 1 =
, X 2 =
,

(X 1,2 =
)

A négyzetes egyenlőtlenségeket alakegyenlőtlenségeknek nevezzük

a x 2 + b x + c > 0,a x 2 + b x + c< 0, (1), (2)

a x 2 + b x + c ≥ 0,a x 2 + b x + c ≤ 0,(3), (4)

A (3) egyenlőtlenség megoldásainak halmazát úgy kapjuk meg, hogy az (1) egyenlőtlenség megoldási halmazait és az egyenletet kombináljuk , a x 2 + b x + c=0. A (4) egyenlőtlenség megoldási halmaza hasonlóképpen található.

Ha egy négyzetháromtag diszkriminánsa a x 2 + b x + c kisebb, mint nulla, akkor a > 0 esetén a trinom minden x-re pozitív R.

Ha a négyzetes trinomnak vannak gyökei (x 1 < х 2 ), akkor a > 0 esetén pozitív a halmazon(-; x 2 )
(X 2; +) és negatív az intervallumon

(x 1; x 2 ). Ha egy< 0, то трехчлен положителен на интервале (х 1; x 2 ) és negatív minden x-re (-; x 1 )
(X 2; +).

1. példa oldja meg az egyenletet ax² - 2 (a - 1) x - 4 \u003d 0.

Ez egy másodfokú egyenlet

Megoldás: Különleges jelentés a = 0.

Nál nél a = 0 lineáris egyenletet kapunk 2x - 4 = 0. Egyetlen gyökere van x = 2.

Nál nél a ≠ 0. Keressük a diszkriminánst.

D \u003d (a-1)² + 4a \u003d (a + 1)²

Ha a = -1, Hogy D = 0 - egy gyökér.

Keresse meg a gyökeret helyettesítéssel a = -1.

-x² + 4x - 4 \u003d 0, vagyis x² -4x + 4 = 0, azt találjuk x=2.

Ha a ≠ - 1, Azt D >0 . A gyökképlet szerint a következőket kapjuk:x=
;

x 1 =2, x 2 = -.

Válasz: Nál nél a=0 és a=-1 egyenletnek egy gyöke van x = 2; nál nél a ≠ 0 és

A ≠ - 1 egyenletnek két gyöke vanx 1 =2, x 2 =-.

2. példa Határozza meg az adott egyenlet gyökeinek számát! x²-2x-8-a=0 paraméterértékektől függően A.

Megoldás. Írjuk át ezt az egyenletet a formába x²-2x-8=a

y \u003d x²-2x-8- a gráf egy parabola;

y =a- vízszintes vonalak családja.

Készítsünk függvénygrafikonokat.

Válasz: Mikor A<-9 , az egyenletnek nincsenek megoldásai; ha a=-9, az egyenletnek egy megoldása van; nál nél a>-9, az egyenletnek két megoldása van.

3. példa Miben A egyenlőtlenség (a - 3) x 2 – 2ax + 3a – 6 >0érvényes x minden értékére?

Megoldás. A négyzetes trinom minden x értékére pozitív, ha

a-3 > 0 és D<0, т.е. при а, удовлетворяющих системе неравенств

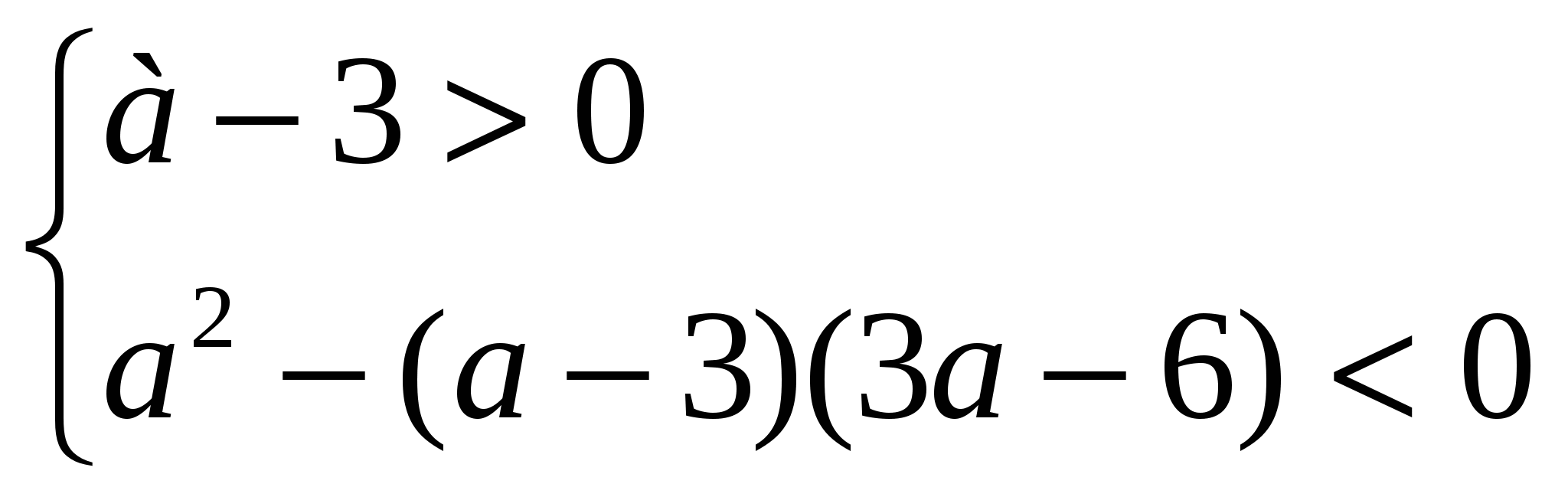
, honnan az következika > 6 .

Válasz.a > 6

3. §. Tört-racionális egyenletek paraméterrel,

lineárisra redukálva

A törtegyenletek megoldását a szokásos séma szerint hajtjuk végre: a törtet egy egész számmal helyettesítjük úgy, hogy az egyenlet mindkét részét megszorozzuk a bal és a jobb oldali rész közös nevezőjével. Ezt követően az egész egyenletet megoldjuk, kivéve az idegen gyököket, vagyis azokat a számokat, amelyek a nevezőt nullára fordítják.

Paraméteres egyenletek esetén ez a probléma bonyolultabb. Itt az idegen gyökök „kiküszöböléséhez” meg kell találni annak a paraméternek az értékét, amelyik a közös nevezőt nullára fordítja, vagyis meg kell oldani a paraméterre vonatkozó megfelelő egyenleteket.

1. példa oldja meg az egyenletet
= 0

Megoldás: D.Z: x +2 ≠ 0, x ≠ -2

x - a \u003d 0, x \u003d a.

Válasz: Nál nél a ≠ - 2, x=a

Nál nél a = -2 nincsenek gyökerei.

2. példa . oldja meg az egyenletet
-
=
(1)

Ez egy tört racionális egyenlet

Megoldás: Jelentése a = 0 különleges. Nál nél a = 0 az egyenlet értelmét veszti, ezért nincs gyökere. Ha a ≠ 0, akkor a transzformációk után az egyenlet a következő alakot veszi fel: x² + 2 (1-a) x + a² - 2a - 3 = 0 (2)- másodfokú egyenlet.

Keressük a diszkriminánst \u003d (1 - a)² - (a² - 2a - 3) \u003d 4, keresse meg az egyenlet gyökereitx 1 = a + 1, x 2 = a - 3.

Az (1) egyenletről a (2) egyenletre való átmenet során az (1) egyenlet definíciós tartománya kibővült, ami idegen gyökerek megjelenéséhez vezethet. Ezért az ellenőrzés szükséges.

Vizsgálat. Kizárás a talált értékek közül x azokat, amelyekben

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

Ha x 1 +1=0, vagyis (a+1) + 1 = 0, Azt a = -2.És így,

nál nél a= -2 , x 1 -

Ha x 1 +2=0, vagyis (a+1)+2=0, Hogy a = -3. Így, at a \u003d - 3, x 1 - az egyenlet idegen gyöke. (1).

Ha x 2 +1=0, vagyis (a - 3) + 1 = 0, Azt a = 2. Így, at a = 2 x 2 - az (1) egyenlet idegen gyöke.

Ha x 2 +2=0, vagyis ( a – 3) + 2 = 0, Hogy a=1. Így, at a = 1,

x 2 - az (1) egyenlet külső gyöke.

Ennek megfelelően a = -3 kapunk x \u003d - 3 - 3 \u003d -6;

nál nél a \u003d - 2 x \u003d -2 – 3= - 5;

nál nél a \u003d 1 x \u003d 1 + 1 \u003d 2;

nál nél a \u003d 2 x \u003d 2 + 1 \u003d 3.

Leírhatod a választ.

Válasz: 1) ha a= -3, Hogy x= -6; 2) ha a= -2, Azt x= -5; 3) ha a=0, akkor nincsenek gyökerek; 4) ha a=1, Azt x=2; 5) ha a=2, Azt x=3; 6) ha a ≠ -3, a ≠ -2, a ≠ 0, a ≠ 1, a ≠ 2, majd x 1 = a + 1, x 2 = a-3.

4. §. Irracionális egyenletek és egyenlőtlenségek

Azokat az egyenleteket és egyenlőtlenségeket, amelyekben a változó a gyökjel alatt található, nevezzük irracionális.

Az irracionális egyenletek megoldása az irracionális egyenletből a racionális egyenletbe való átmenetre redukálódik, ha az egyenlet mindkét oldalát hatványra emeljük, vagy a változót megváltoztatjuk. Ha az egyenlet mindkét oldalát egyenletes hatványra emeljük, idegen gyökök jelenhetnek meg. Ezért ennek a módszernek a használatakor az összes talált gyökeret ellenőrizni kell az eredeti egyenletbe való behelyettesítéssel, figyelembe véve a paraméterértékek változásait.

Típusegyenlet
=g (x ) ekvivalens a rendszerrel

Az f (x) ≥ 0 egyenlőtlenség az f (x) = g 2 (x) egyenletből következik.

Az irracionális egyenlőtlenségek megoldása során a következő ekvivalens transzformációkat használjuk:

≤ g(x)

≥g(x)

1. példa Oldja meg az egyenletet
= x + 1 (3)

Ez egy irracionális egyenlet

Megoldás: Az aritmetikai gyök meghatározása szerint a (3) egyenlet ekvivalens a rendszerrel
.

Nál nél a = 2 a rendszer első egyenlete alakja 0 x = 5, vagyis nincs megoldása.

Nál nél a≠ 2 x=
. Nézzük meg, milyen értékekreA talált értéketx kielégíti az egyenlőtlenségetx ≥ -1:
≥ - 1,
≥ 0,

ahol a ≤ vagy a > 2.

Válasz: Nál nél a≤, a > 2 x=
, nál nél < а ≤ 2 az egyenletnek nincsenek megoldásai.

2. példa oldja meg az egyenletet
= a (4. melléklet)

Megoldás. y =

y = a vízszintes vonalak családja.

Készítsünk függvénygrafikonokat.

Válasz: nál nél A<0 - nincsenek megoldások

nál nél A≥ 0 - egy megoldás.

3. példa . Oldjuk meg az egyenlőtlenséget(a+1)
<1.

Megoldás. O.D.Z. x ≤ 2. Ha a+1 ≤0, akkor az egyenlőtlenség minden megengedett értékre érvényes x. Ha a+1>0, Azt

(a+1)
<1.

<

ahol x (2-
2

Válasz. x (- ;2a (-;-1, x (2-
2

nál nél A (-1;+).

5. § Trigonometrikus egyenletek és egyenlőtlenségek.

Íme a képletek a legegyszerűbb trigonometrikus egyenletek megoldásához:

Sinx = a
x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = a
x = ± arccos a + 2 πn, n Z, ≤1. (2)

Ha >1, akkor az (1) és (2) egyenletnek nincs megoldása.

tan x = a
x= arctg a + πn, n Z, a R

ctg x = a
x = arcctg a + πn, n Z, a R

Minden standard egyenlőtlenséghez megadjuk a megoldások halmazát:

1. sin x > a
arcsin a + 2 n Z,

nál nél a <-1, x R ; nál nél a ≥ 1, nincsenek megoldások.

2. . bűn x< a
π - arcsin a + 2 πnZ,

a≤-1 esetén nincs megoldás; amikor a>1,x R

3. kötözősaláta x > a
- arccos a + 2 pn < x < arccos a + 2 pn , n Z ,

nál nél A<-1, x R ; nál nél a ≥ 1 , nincsenek megoldások.

4. cos x arccos a+ 2 nZ,

nál nél a≤-1 , nincsenek megoldások; nál néla > 1, x R

5. tg x > a, arctg a + πnZ

6.tg x< a, -π/2 + πn Z

Példa1. megtalálja A, amelyre ennek az egyenletnek van megoldása:

Cos 2 x + 2(a-2) cosx + a 2 - 4a - 5 \u003d 0.

Megoldás. Az egyenletet a formába írjuk

Val velos 2 x + (2 a -4) cosx +(a – 5)(а+1) =0, négyzetként megoldva azt kapjuk cosx = 5-AÉs cosx = -a-1.

Az egyenlet cosx = 5- A megoldásokat kínál -1≤ 5-A ≤1
4≤ A≤ 6, és az egyenlet cosx = - a-1 feltéve -1≤ -1-A ≤ 1
-2 ≤ A ≤0.

Válasz. A -2; 0
4; 6

2. példa Miben blétezik olyan, hogy az egyenlőtlenség
+ b> 0 teljesül minden x ≠ eseténpn , n Z .

Megoldás. Tegyük fel A= 0. Az egyenlőtlenség teljesül, ha b >0. Mutassuk meg, hogy egyetlen b ≤0 sem felel meg a feladat feltételeinek. Valóban, elég, ha x =-et teszünk π /2, Ha A <0, и х = - π /2 nál nél A ≥0.

Válasz.b > 0

6. § Exponenciális egyenletek és egyenlőtlenségek

1. Egyenlet h(x) f ( x ) = h(x) g ( x) nál nél h(x) > 0 két rendszer kombinációjának felel meg
És

2. Egy adott esetben (h (x)= a ) az egyenlet A f(x) = A g(x) at A> 0, egyenértékű két rendszer kombinációjával

És

3. Egyenlet A f(x) = b , Ahol A > 0, a ≠1, b>0, ekvivalens az egyenlettel

f(x)= log a b . Esemény A Az =1 értéket külön kell figyelembe venni.

A legegyszerűbb exponenciális egyenlőtlenségek megoldása a fok tulajdonságon alapul. A forma egyenlőtlenségef(a x ) > 0 a változó megváltoztatásávalt= a x az egyenlőtlenségek rendszerének megoldására redukálódik
majd a megfelelő legegyszerűbb exponenciális egyenlőtlenségek megoldására.

Egy nem szigorú egyenlőtlenség megoldása során a megfelelő egyenlet gyökeit kell hozzáadni a szigorú egyenlőtlenség megoldásainak halmazához. Mint az egyenletek megoldásánál minden olyan példában, amely a kifejezést tartalmazza A f (x ) , feltételezzük A> 0. Eset A= 1-et külön kell figyelembe venni.

1. példa . Miben A egyenlet 8 x =
csak pozitív gyökerei vannak?

Megoldás. Egynél nagyobb bázisú exponenciális függvény tulajdonsága alapján x>0
8 x >1

>1

>0, honnana (1,5;4).

Válasz. a (1,5;4).

2. példa Oldja meg az egyenlőtlenséget a 2 ∙2 x > a

Megoldás. Vegyünk három esetet:

1. A< 0 . Mivel az egyenlőtlenség bal oldala pozitív, a jobb oldala pedig negatív, az egyenlőtlenség bármely x-re érvényes R.

2. a=0. Nincsenek megoldások.

3. A > 0 . a 2 ∙2 x > a
2 x >
x > -log 2 a

Válasz. x R nál nél A > 0; nincs megoldás erre a =0; x (- log 2 a; +) nál néla > 0 .

7. § Logaritmikus egyenletek és egyenlőtlenségek

Mutassunk be néhány megoldásban használt ekvivalenciát logaritmikus egyenletek és egyenlőtlenségek.

1. A log f (x) g (x) \u003d log f (x) h (x) egyenlet ekvivalens a rendszerrel

Különösen, ha A >0, A≠1, akkor

log a g(x)=log a h(x)

2. Az egyenlet log a g(x)=b
g(x)=a b ( A >0, a ≠ 1, g(x) >0).

3. Egyenlőtlenség log f ( x ) g (x) ≤ log f ( x ) h(x) egyenértékű két rendszer kombinációjával:
És

Ha egy, b számok, a >0, a ≠1, akkor

log a f(x) ≤ b

log a f(x) > b

1. példa Oldja meg az egyenletet

Megoldás. Keressük az ODZ-t: x > 0, x ≠ A 4 , a > 0, A≠ 1. Alakítsa át az egyenletet

log x - 2 = 4 - log a x
log x + log a x– 6 = 0, honnan log a x = - 3

x = A-3 és log a x = 2
x = A 2. Feltétel x = A 4
A – 3 = A 4 vagy A 2 = A 4 nem hajtották végre az ODZ-n.

Válasz: x = A-3, x = A 2 órakor A (0; 1)
(1; ).

2. példa . Keresse meg a legmagasabb értéket A, amelyre az egyenlet

2 log -
+ a = 0-nak vannak megoldásai.

Megoldás. Cseréljük
= tés kapjuk meg a 2. másodfokú egyenletett 2 – t + a = 0. Megoldás, azt találjukD = 1-8 a . Fontolgat D≥0, 1-8 A ≥0
A ≤.

Nál nél A = a másodfokú egyenletnek van gyöket= >0.

Válasz. A =

3. példa . Oldja meg az egyenlőtlenségetlog(x 2 – 2 x + a ) > - 3

Megoldás. Oldjuk meg az egyenlőtlenségek rendszerét

Négyzetes trinomikus x gyökei 1,2 = 1 ±
az övék 3,4 = 1 ±
.

Kritikus paraméterértékek: A= 1 és A= 9.

Legyen tehát X 1 és X 2 az első és a második egyenlőtlenség megoldáshalmaza

X 1
x 2 = X az eredeti egyenlőtlenség megoldása.

0-nál< a <1 Х 1 = (- ;1 -
)
(1 +
; +), nál nélA> 1 x 1 = (-;+).

0-nál< a < 9 Х 2 = (1 -
; 1 +
), nál nélA≥9 Х 2 – nincs megoldás.

Tekintsünk három esetet:

1. 0< a ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < a < 9 Х = (1 -
;1 +
).

3. a≥ 9 Х – nincs megoldás.

HASZNÁLJON feladatokat

Magas szintű C1, C2

1. példa Keresse meg az összes értéket R, amelyre az egyenlet

R ∙ ctg 2x+2sinx+ p= 3-nak legalább egy gyöke van.

Megoldás. Alakítsuk át az egyenletet

R ∙ (
-1)+2sinx+ p\u003d 3, sinx \u003d t, t
, t 0.

- p+ 2t + p = 3, + 2t = 3, 3 -2t = , 3t2 – 2t3 = p .

Hadd f(y) = 3 t 2 – 2 t 3 . Keressük meg a függvényértékek halmazátf(x) tovább

. nál nél / = 6 t – 6 t 2 , 6 t - 6 t 2 = 0, t 1 =0, t 2 = 1. f(-1) = 5, f(1) = 1.

Nál nél t
, E(f) =
,

Nál nél t
, E(f) =
, vagyis mikor t

, E(f) =
.

A 3. egyenlethezt 2 – 2 t 3 = p (tehát az adott) volt legalább egy szükséges és elegendő gyökp E(f), vagyis p
.

Válasz.
.

2. példa

A paraméter milyen értékeinélA az egyenlet log
(4 x 2 – 4 a + a 2 +7) = 2-nek pontosan egy gyöke van?

Megoldás. Alakítsuk át az egyenletet egy ekvivalenssé:

4x 2-4 a + a 2 +7 \u003d (x 2 + 2) 2.

Vegye figyelembe, hogy ha egy bizonyos x szám a kapott egyenlet gyöke, akkor az - x szám ennek az egyenletnek a gyöke is. Feltétel szerint ez nem kivitelezhető, így az egyetlen gyök a 0.

Keressük A.

4∙ 0 2 - 4a + a 2 +7 = (0 2 + 2) 2 ,

a 2 - 4a +7 = 4, a 2 - 4a +3 = 0, a 1 = 1, a 2 = 3.

Vizsgálat.

1) a 1 = 1. Ekkor az egyenlet a következőképpen alakul:log
(4 x 2 +4) =2. Megoldjuk

4x 2 + 4 \u003d (x 2 + 2) 2, 4x 2 + 4 \u003d x 4 + 4x 2 + 4, x 4 \u003d 0, x \u003d 0 az egyetlen gyök.

2) a 2 = 3. Az egyenlet így néz ki:log
(4 x 2 +4) =2
x = 0 az egyetlen gyök.

Válasz. 1; 3

Magas szintű C4, C5

3. példa Keresse meg az összes értéket R, amely alatt az egyenlet

x 2 - ( R+ 3)x + 1= 0-nak egész gyökei vannak, és ezek a gyökök az x 3 - 7 egyenlőtlenség megoldásai R x 2 + 2x 2 - 14 R x - 3x +21 R ≤ 0.

Megoldás. Legyen x 1, x 2 az x egyenlet egész gyökei 2 – (R + 3)x + 1= 0. Ekkor a Vieta képlet alapján x 1 + x 2 = R + 3, x 1 ∙ x 2 = 1. Két x egész szám szorzata 1 , X 2 csak két esetben lehet egyenlő eggyel: x 1 = x 2 = 1 vagy x 1 = x 2 = - 1. Ha x 1 = x 2 = 1, akkorR + 3 = 1+1 = 2
R = -1; ha x 1 = x 2 = - 1, akkorR + 3 = - 1 – 1 = - 2
R = - 5. Ellenőrizze, hogy az x egyenlet gyökei-e 2 – (R + 3)x + 1= 0 ezen egyenlőtlenség megoldásaival leírt esetekben. Az esethezR = - 1, x 1 = x 2 = 1 van nálunk

1 3 - 7 ∙ (- 1) ∙ 1 2 +2 ∙ 1 2 - 14 ∙ (- 1) ∙ 1 - 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 - igaz; az esethez R\u003d - 5, x 1 \u003d x 2 \u003d - 1 van (- 1) 3 - 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 - 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 helyes. Tehát a probléma feltétele csak teljesül R= - 1 és R = - 5.

Válasz.R 1 = - 1 és R 2 = - 5.

4. példa Keresse meg az összes pozitív paraméterértéket A, amelynél az 1-es szám a függvény tartományába tartozik

nál nél = (A
- A
).

Munka típusa: 18

Feltétel

Az a paraméter mely értékeire vonatkozik az egyenlőtlenség

\log_(5)(4+a+(1+5a^(2)-\cos^(2)x) \cdot\sin x - a \cos 2x) \leq 1érvényes az x összes értékére?

Megoldás megjelenítése

Megoldás

Ez az egyenlőtlenség megegyezik a kettős egyenlőtlenséggel 0 < 4+a+(5a^{2}+\sin^{2}x) \sin x+ a(2 \sin^(2)x-1) \leq 5 .

Legyen \sin x=t , akkor megkapjuk az egyenlőtlenséget:

4 < t^{3}+2at^{2}+5a^{2}t \leq 1 \: (*) , aminek érvényesnek kell lennie a -1 \leq t \leq 1 összes értékére. Ha a=0 , akkor a (*) egyenlőtlenség érvényes bármely t\in [-1;1]-re.

Legyen egy \neq 0 . Az f(t)=t^(3)+2at^(2)+5a^(2)t függvény a [-1;1] intervallumon növekszik, mivel az f"(t)=3t^(2)+ derivált 4at +5a^(2) > 0 t \in \mathbb(R) és a \neq 0 összes értékére (D megkülönböztető< 0 и старший коэффициент больше нуля).

A (*) egyenlőtlenség t \in [-1;1]-re érvényes a feltételek mellett

\begin(esetek) f(-1) > -4, \\ f(1) \leq 1, \\ a \neq 0; \end(esetek)\:\bal jobbra nyíl \begin(esetek) -1+2a-5a^(2) > -4, \\ 1+2a+5a^(2) \leq 1, \\ a \neq 0; \end(esetek)\:\bal jobbra nyíl \begin(esetek) 5a^(2)-2a-3< 0, \\ 5a^{2}+2a \leq 0, \\ a \neq 0; \end{cases}\: \Leftrightarrow -\frac(2)(5) \leq a< 0 .

Tehát a feltétel teljesül, ha -\frac(2)(5) \leq a \leq 0 .

Válasz

\left [-\frac(2)(5); 0\jobbra]

Forrás: "Matematika. Felkészülés a vizsgára-2016. profilszint. Szerk. F. F. Lysenko, S. Yu. Kulabukhova.

Munka típusa: 18
Téma: Egyenlőtlenségek paraméterrel

Feltétel

Keresse meg az a paraméter összes értékét, amelyek mindegyikére az egyenlőtlenség vonatkozik

x^2+3|x-a|-7x\leqslant -2a

egyedi megoldása van.

Megoldás megjelenítése

Megoldás

Az egyenlőtlenség egyenlő az egyenlőtlenségek rendszereinek halmazával

\left[\!\!\begin(array)(l) \begin(cases) x \geqslant a, \\ x^2+3x-3a-7x+2a\leqslant0; \end(esetek) \\ \begin(esetek)x \left[\!\!\begin(array)(l) \begin(cases) x \geqslant a, \\ x^2-4x-a\leqslant0; \end(esetek) \\ \begin(esetek)x \left[\!\!\begin(array)(l) \begin(cases) a \leqslant x, \\ a\geqslant x^2-4x; \end(esetek) \\ \begin(cases)a>x, \\ a\leqslant -\frac(x^2)(5)+2x. \end(esetek)\end(tömb)\jobbra.

Az Oxa koordinátarendszerben függvénygráfokat készítünk a=x, a=x^2-4x, a=-\frac(x^2)(5)+2x.

A kapott halmazt a függvénygráfok közé zárt pontok teljesítik a=x^2-4x, a=-\frac(x^2)(5)+2x x\in (árnyékolt terület).

A grafikon alapján meghatározzuk: az eredeti egyenlőtlenségnek egyedi megoldása van a=-4 és a=5 esetén, mivel az árnyékolt területen egyetlen pont lesz, amelynek a ordinátája -4 és 5.

Tanfolyami munka

Művész: Bugrov S.K.

Számos fizikai folyamat és geometriai mintázat tanulmányozása gyakran a paraméterekkel kapcsolatos problémák megoldásához vezet. Egyes egyetemek egyenleteket, egyenlőtlenségeket és ezek rendszereit is belefoglalják a vizsgajegyekbe, amelyek gyakran nagyon összetettek, és nem szabványos megoldást igényelnek. Az iskolában az iskolai matematika tantárgy egyik legnehezebb szakaszát csak néhány fakultatív órán veszik figyelembe.

A munka elkészítése során a téma mélyebb tanulmányozását tűztem ki célul, azonosítva a legracionálisabb megoldást, amely gyorsan válaszhoz vezet. Véleményem szerint a grafikus módszer kényelmes és gyors módja egyenletek és paraméterekkel való egyenlőtlenségek megoldásának.

Összefoglalómban a gyakran előforduló egyenlettípusokat, egyenlőtlenségeket és ezek rendszereit veszem figyelembe, és remélem, hogy a munka során megszerzett ismereteim segítségemre lesznek az iskolai vizsgák letételekor és az egyetemre való felvételkor.

§ 1. Alapvető definíciók

Tekintsük az egyenletet

¦(a, b, c, …, k, x)=j(a, b, c, …, k, x), (1)

ahol a, b, c, …, k, x változók.

Bármilyen változó értékrendszer

a = a0, b = b0, c = c0, …, k = k0, x = x0,

amely szerint ennek az egyenletnek a bal és jobb része is valós értéket vesz fel, az a, b, c, ..., k, x változók megengedett értékeinek rendszerének nevezzük. Legyen A az a összes megengedett értékének halmaza, B a b összes megengedett értékének halmaza, stb., X az x összes megengedett értékének halmaza, azaz. aОА, bОB, …, xОX. Ha az A, B, C, …, K halmazok mindegyike kiválaszt és rögzít egy a, b, c, …, k értéket, és behelyettesíti őket az (1) egyenletbe, akkor x egyenletet kapunk, azaz. egyenlet egy ismeretlennel.

Az egyenlet megoldása során állandónak tekintett a, b, c, ..., k változókat paramétereknek, magát az egyenletet pedig paramétereket tartalmazó egyenletnek nevezzük.

A paramétereket a latin ábécé első betűivel jelöljük: a, b, c, d, …, k, l, m, n, az ismeretleneket pedig x, y, z betűkkel.

Egy egyenlet paraméterekkel való megoldása azt jelenti, hogy jelezzük, hogy a paraméterek milyen értékeinél léteznek megoldások és mik azok.

Két azonos paramétert tartalmazó egyenletet egyenértékűnek mondunk, ha:

a) a paraméterek azonos értékeihez van értelme;

b) az első egyenlet minden megoldása a második egyenlet megoldása és fordítva.

§ 2. Megoldási algoritmus.

Keresse meg az egyenlet tartományát.

Az a-t x függvényében fejezzük ki.

Az xOa koordinátarendszerben elkészítjük az a=¦(x) függvény grafikonját azokra az x értékekre, amelyek az egyenlet definíciós tartományába tartoznak.

Megtaláljuk az a=c egyenes metszéspontjait, ahol cÎ(-¥;+¥) az a=¦(x) függvény grafikonjával Ha az a=c egyenes metszi az a=¦(x) gráfot , akkor meghatározzuk a metszéspontok abszcisszáját. Ehhez elég megoldani az a=¦(x) egyenletet x-hez képest.

Leírjuk a választ.

I. Oldja meg az egyenletet!

(1)

Mivel x \u003d 0 nem az egyenlet gyöke, így megoldhatjuk az egyenletet a:

vagy

A függvénygráf két „összeragasztott” hiperbola. Az eredeti egyenlet megoldásainak számát a megszerkesztett egyenes és az y=a egyenes metszéspontjainak száma határozza meg.

Ha egy О (-¥;-1]И(1;+¥)И

, akkor az y=a egyenes egy pontban metszi az (1) egyenlet grafikonját. Ennek a pontnak az abszcisszáját az x egyenlet megoldása során találjuk meg.

Így ezen az intervallumon az (1) egyenletnek megvan a megoldása

. , akkor az y=a egyenes két pontban metszi az (1) egyenlet grafikonját. Ezeknek a pontoknak az abszcisszáit a és egyenletekből találhatjuk meg, megkapjuk és . , akkor az y=a egyenes nem metszi az (1) egyenlet grafikonját, ezért nincs megoldás.

Ha egy О (-¥;-1]И(1;+¥)И

, Az ; , Az , ; , akkor nincsenek megoldások.

II. Keresse meg az a paraméter összes értékét, amelyre az egyenlet vonatkozik

három különböző gyökere van.

Az egyenlet átírása így

és figyelembe véve egy pár függvényt, láthatja, hogy az a paraméter kívánt értékei és csak ezek fognak megfelelni a függvény grafikonjának azon pozícióinak, ahol pontosan három metszéspontja van a függvény grafikonjával .

Az xOy koordinátarendszerben ábrázoljuk a függvényt

). Ehhez ábrázolhatjuk formában, és négy felmerülő esetet figyelembe véve ezt a függvényt alakba írjuk.

Mivel a függvény grafikonja

- ez egy egyenes, amelynek dőlésszöge az Ox tengelyhez képest egyenlő, és az Oy tengelyt egy (0, a) koordinátájú pontban metszi, arra a következtetésre jutunk, hogy a három jelzett metszéspont csak akkor érhető el, ha ez az egyenes megérinti a függvény grafikonját. Ezért megtaláljuk a származékot.

III. Keresse meg az a paraméter összes értékét, amelyek mindegyikére az egyenletrendszer

megoldásai vannak.

A rendszer első egyenletéből kapjuk

Ezért ez az egyenlet a „félparabolák” családját határozza meg – a parabola jobb oldali ágai „csúsznak” csúcsaikkal az abszcissza tengely mentén.

Jelölje ki a teljes négyzeteket a második egyenlet bal oldalán, és szorozza azt

A sík pontjainak halmaza

a második egyenletet kielégítő két egyenes és

Nézzük meg, hogy a paraméter mely értékeihez van a „félparabola” családból származó görbének legalább egy közös pontja a kapott egyenesek egyikével.

Egyenlőtlenségek megoldása paraméterrel.

Az ax > b, ax alakú egyenlőtlenségek< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются lineáris egyenlőtlenségek.

A lineáris egyenlőtlenségek paraméterrel történő megoldásának elvei nagyon hasonlóak a lineáris egyenletek paraméterrel történő megoldásának elveihez.

1. példa

Oldja meg az 5x - a > ax + 3 egyenlőtlenséget.

Megoldás.

Először is alakítsuk át az eredeti egyenlőtlenséget:

5x - ax > a + 3, az egyenlőtlenség bal oldalán lévő zárójelekből kivesszük x-et:

(5 - a) x > a + 3. Tekintsük most az a paraméter lehetséges eseteit:

Ha a > 5, akkor x< (а + 3) / (5 – а).

Ha a = 5, akkor nincs megoldás.

Ha egy< 5, то x >(a + 3) / (5 - a).

Ez a megoldás lesz a válasz az egyenlőtlenségre.

2. példa

Oldja meg az x(a - 2) / (a - 1) - 2a / 3 ≤ 2x - a egyenlőtlenséget, ha a ≠ 1.

Megoldás.

Alakítsuk át az eredeti egyenlőtlenséget:

x(a - 2) / (a - 1) - 2x ≤ 2a/3 - a;

Ah/(a – 1) ≤ -a/3. Az egyenlőtlenség mindkét részét megszorozzuk (-1)-gyel, így kapjuk:

ax/(a – 1) ≥ a/3. Vizsgáljuk meg az a paraméter lehetséges eseteit:

1 eset. Legyen a/(a – 1) > 0 vagy a € (-∞; 0)ᴗ(1; +∞). Ekkor x ≥ (а – 1)/3.

2. eset. Legyen a/(а – 1) = 0, azaz. a = 0. Ekkor x bármely valós szám.

3. eset. Legyen a/(а – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Válasz: x € [(a - 1) / 3; +∞) egy € esetén (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] euróért (0; 1);
x € R a = 0 esetén.

3. példa

Oldja meg az |1 + x| egyenlőtlenséget ≤ ax x-hez képest.

Megoldás.

Abból a feltételből következik, hogy az egyenlőtlenségi tengely jobb oldalának nem negatívnak kell lennie, azaz. ax ≥ 0. A modulo kiterjesztési szabály szerint az egyenlőtlenség |1 + x| ≤ ax kettős egyenlőtlenségünk van

Ax ≤ 1 + x ≤ ax. Az eredményt átírjuk egy rendszer formájában:

(ax ≥ 1 + x;
(-ax ≤ 1 + x.

Alakítsuk át a következő formára:

((а – 1)x ≥ 1;
((a + 1)x ≥ -1.

Az eredményül kapott rendszert intervallumokon és pontokon vizsgáljuk (1. ábra):

A ≤ -1 x € (-∞; 1/(a - 1)] esetén.

-1-nél< а < 0 x € [-1/(а – 1); 1/(а – 1)].

Amikor a \u003d 0 x \u003d -1.

0-nál< а ≤ 1 решений нет.

Grafikus módszer egyenlőtlenségek megoldására

Az ábrázolás nagymértékben leegyszerűsíti a paramétert tartalmazó egyenletek megoldását. A grafikus módszer alkalmazása az egyenlőtlenségek paraméterrel történő megoldásában még áttekinthetőbb és célszerűbb.

Az f(x) ≥ g(x) alakú egyenlőtlenségek grafikus megoldása annak az x változónak az értékeinek megtalálását jelenti, amelyre az f(x) függvény grafikonja a g(x) függvény grafikonja felett van. Ehhez mindig meg kell találni a gráfok metszéspontjait (ha vannak).

1. példa

Oldja meg az |x + 5| egyenlőtlenséget< bx.

Megoldás.

Az y = |x + 5| függvények grafikonjait készítjük és y = bx (2. ábra). Az egyenlőtlenség megoldása az x változó azon értékei lesz, amelyekre az y függvény grafikonja = |x + 5| az y = bx függvény grafikonja alatt lesz.

Az ábrán látható:

1) b > 1 esetén az egyenesek metszik egymást. Ezen függvények grafikonjai metszéspontjának abszcisszája az x + 5 = bx egyenlet megoldása, ahonnan x = 5/(b - 1). Az y \u003d bx grafikon az (5 / (b - 1); +∞) intervallum x esetén magasabb, ami azt jelenti, hogy ez a halmaz az egyenlőtlenség megoldása.

2) Hasonlóképpen azt találjuk, hogy -1< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) b ≤ -1 x € esetén (-∞; 5/(b - 1)).

4) 0 ≤ b ≤ 1 esetén a gráfok nem metszik egymást, ami azt jelenti, hogy az egyenlőtlenségnek nincs megoldása.

Válasz: x € (-∞; 5/(b - 1)) b ≤ -1 esetén;
x € (-5/(b + 1); 5/(b – 1)) -1-nél< b < 0;
0 ≤ b ≤ 1-re nincs megoldás; x € (5/(b – 1); +∞), ha b > 1.

2. példa

Oldja meg az a(a + 1)x > (a + 1)(a + 4) egyenlőtlenséget.

Megoldás.

1) Keressük meg az a paraméter "vezérlő" értékeit: a 1 = 0, a 2 = -1.

2) Oldjuk meg ezt az egyenlőtlenséget a valós számok minden részhalmazán: (-∞; -1); (-1); (-10); (0); (0; +∞).

a) a< -1, из данного неравенства следует, что х >(a + 4)/a;

b) a \u003d -1, akkor ez az egyenlőtlenség 0 x > 0 alakot ölt - nincs megoldás;

c)-1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, akkor ez az egyenlőtlenség 0 x > 4 alakú – nincs megoldás;

e) a > 0, ez az egyenlőtlenség azt jelenti, hogy x > (a + 4)/a.

3. példa

Oldja meg a |2 – |x|| egyenlőtlenséget< a – x.

Megoldás.

Ábrázoljuk az y = |2 – |x|| függvényt (3. ábra)és vegye figyelembe az y \u003d -x + a sor helyének minden lehetséges esetét.

Válasz: az egyenlőtlenségnek nincs megoldása a ≤ -2-re;
x € (-∞; (a - 2)/2) egy €-val (-2; 2]);
x € (-∞; (a + 2)/2), ha a > 2.

Különböző problémák, egyenletek, paraméterekkel való egyenlőtlenségek megoldása során jelentős számú heurisztikus technika nyílik meg, amelyek aztán a matematika bármely más ágában sikeresen alkalmazhatók.

A paraméterekkel kapcsolatos problémák fontos szerepet játszanak a logikus gondolkodás és a matematikai kultúra kialakításában. Éppen ezért, miután elsajátította a paraméterekkel kapcsolatos problémák megoldásának módszereit, sikeresen megbirkózik más problémákkal.

Van kérdésed? Nem tudja, hogyan oldja meg az egyenlőtlenségeket?
Segítséget kérni egy oktatótól -.
Az első óra ingyenes!

blog.site, az anyag teljes vagy részleges másolásakor a forrásra mutató hivatkozás szükséges.

Sorozat "Tanuljuk meg a problémákat paraméterrel megoldani"

IV. Másodfokú egyenletek és egyenlőtlenségek paraméterrel

IV.1. Alapfogalmak

Meghatározás. Egy (1) alakú függvény, ahol , , a paraméter adott függvényei A, amelyeket a definíciós tartományuk metszéspontjában tekintünk, másodfokú függvényt hívunk a paraméterrel A.

Példák.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

Meghatározás. A másodfokú függvény (1) altartománya a paraméterrel A meg fogjuk érteni az értékpárok egész halmazát xÉs A kedves ( x; A), amelyek mindegyikénél a kifejezés nem veszíti el jelentését.

Állítsuk be az 1-10 függvények definícióinak tartományait.

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

Ha a paraméter a numerikus értékek egyikét veszi át, akkor az (1) függvény a numerikus együtthatós függvények egyike lesz:

; ; ;
; ; ; ,

Ahol k, b, c valós számok.

Figyeljünk arra, hogy a paraméter egyes értékeinél a paraméterrel rendelkező másodfokú függvény vagy paraméter nélküli másodfokú függvény, vagy lineáris függvény formáját ölti.

Mivel egy paraméterrel rendelkező másodfokú függvény leggyakrabban másodfokú vagy lineáris függvénycsaládot "generál" numerikus együtthatókkal, akkor a másodfokú függvény grafikonjai paraméterrel, ennek a családnak a grafikonkészletét fogjuk érteni.

Meghatározás. A egy (1) alakú egyenlet, ahol , , a paraméter adott függvényei A definíciós területeik metszéspontjában tekintendők.

Az együtthatók vagy metszéspontok egy része különösen szám lehet.

Példák.

, (1)
, (2)
, (3)
, (4)
. (5)

A másodfokú függvény paraméteres definícióját felhasználva megadható egy paraméteres másodfokú egyenlet ilyen definíciója.

Meghatározás. Másodfokú egyenlet paraméterrel A alakú egyenletnek nevezzük, ahol egy másodfokú függvény paraméterrel A.

Ha , akkor az (1) egyenlet hagyományos értelemben másodfokú, azaz. másodfokú.
Ha , akkor az (1) egyenlet lineárissá válik.

A paraméter összes érvényes értékéhez A, amelyre és az ismert képletek szerint az (1) egyenlet gyökére kifejezéseket kapunk a paraméter szempontjából.

Azok a jelentések A, amelyeknél külön-külön kell figyelembe venni, mint speciális eseteket.
Így például az (5) at egyenlet a következőt veszi fel, ahonnan .

IV.2. Másodfokú egyenletek paraméterrel

№1. Oldja meg az egyenletet.

– egyenlet-következmény. Kapunk: , .

A koordinátarendszerben ( ó) fejezze be a megoldást. (1. ábra)

Válasz: 1. Ha , akkor .

2. Ha , akkor .

3. Ha , , akkor , .

№2. Keresse meg a paraméter értékét A, amelyre az egyenletnek egyetlen gyöke van. Ha több ilyen érték van, írja be válaszában ezek összegét.

Ez az egyenlet egy ekvivalens rendszerre redukálódik:

Hozzuk formába: és oldjuk meg grafikusan a koordinátarendszerben ( hoa). (2. ábra).

Az egyenletnek egyetlen gyöke van , és .

№3. Keresse meg az összes értéket xúgy, hogy a paraméter bármely értékére A, amely nem tartozik a (0; 2] intervallumhoz, a kifejezés nem egyenlő a kifejezéssel. (USE-2007).

Fogalmazza meg újra a problémát: „Keresse meg az összes értéket xúgy, hogy a paraméter bármely értékére az egyenlet nincsenek gyökerei.
Expressz A keresztül x:

1) Hagyjuk. Akkor . Ezért az egyenletnek gyökerei vannak. Tehát nem felel meg a feltételnek.
2) Hagyjuk. Akkor . A koordinátarendszert használjuk ( hoa). (3. ábra).

A feltétel teljesül.