Egy függvény extrém pontjai online. Két változó függvényének szélsőértéke

Ebből a cikkből az olvasó megtudhatja, mi a funkcionális érték szélsősége, valamint a gyakorlati tevékenységekben való felhasználásának jellemzői. Egy ilyen fogalom tanulmányozása rendkívül fontos a magasabb matematika alapjainak megértéséhez. Ez a téma alapvető a kurzus mélyebb tanulmányozásához.

Kapcsolatban áll

Mi az extrémum?

Az iskolai kurzusban a „szélsőség” fogalmának számos meghatározása megtalálható. Ennek a cikknek az a célja, hogy a szó legmélyebb és legtisztább megértését nyújtsa azok számára, akik nem ismerik a kérdést. Tehát a kifejezés azt jelenti, hogy a funkcionális rés mennyit szerez minimális ill maximális érték egyik vagy másik készleten.

Az extrémum egy függvény minimumértéke és maximuma egyszerre. Van egy minimumpont és egy maximumpont, vagyis az argumentum szélső értékei a grafikonon. A főbb tudományok, amelyek ezt a fogalmat használják:

• statisztika;
• gépvezérlés;
• ökonometria.

Az extrém pontok fontos szerepet játszanak az adott függvény sorrendjének meghatározásában. A koordinátarendszer a grafikonon be a javából a szélső pozíció változását mutatja a funkcionalitás változásától függően.

A derivált függvény szélsőértéke

Létezik olyan jelenség is, mint a „származék”. Meg kell határozni a szélsőpontot. Fontos, hogy ne keverjük össze a minimum vagy maximum pontot a legmagasabb és legalacsonyabb értékkel. Ezek különböző fogalmak, bár hasonlónak tűnhetnek.

A függvény értéke a fő tényező a maximális pont megtalálásának meghatározásában. A származék nem értékekből alakul ki, hanem kizárólag az egyik vagy másik sorrendben elfoglalt szélső helyzetéből.

Maga a derivált ezek alapján a szélsőpontok alapján kerül meghatározásra, nem pedig a legnagyobb vagy legkisebb érték alapján. Az orosz iskolákban nem húzzák meg egyértelműen a határvonalat e két fogalom között, ami befolyásolja a téma általános megértését.

Tekintsük most az „akut szélsőség” fogalmát. Ma van egy akut minimumérték és egy akut maximum érték. A meghatározást a függvény kritikus pontjainak orosz besorolása szerint adjuk meg. A szélsőségpont fogalma az alapja a kritikus pontok megtalálásának a gráfon.

Egy ilyen fogalom meghatározásához Fermat tételéhez folyamodnak. Ez a legfontosabb a szélsőséges pontok tanulmányozásában, és világos képet ad létezésükről ilyen vagy olyan formában. Az extrémség biztosítása érdekében fontos bizonyos feltételeket megteremteni a grafikonon a csökkenéshez vagy növekedéshez.

A „maximum pont megtalálása” kérdés pontos megválaszolásához kövesse az alábbi irányelveket:

1. A definíció pontos tartományának megtalálása a gráfon.
2. Keresse meg a függvény deriváltját és a szélsőpontot.
3. Oldja meg a standard egyenlőtlenségeket arra a tartományra, ahol az argumentum található.
4. Legyen képes igazolni, hogy egy gráf egy pontja mely függvényekben definiált és folytonos.

Figyelem! Egy függvény kritikus pontjának keresése csak akkor lehetséges, ha van legalább másodrendű derivált, amit a szélsőpont jelenlétének magas aránya biztosít.

Egy függvény szélsőértékének szükséges feltétele

A szélsőség létezéséhez fontos, hogy legyen minimum és maximum pont is. Ha ezt a szabályt csak részben tartják be, akkor a szélsőség fennállásának feltétele sérül.

Minden funkciót bármely pozícióban meg kell különböztetni, hogy azonosítani lehessen új jelentését. Fontos megérteni, hogy egy pont nullára kerülése nem a megkülönböztethető pont megtalálásának fő elve.

Az akut extrémum, valamint a függvény minimuma rendkívül fontos szempont egy matematikai probléma szélsőséges értékeket használó megoldásában. Ennek az összetevőnek a jobb megértése érdekében fontos hivatkozni a táblázatos értékekre a funkcionalitás meghatározásához.

Teljes jelentéskutatás

Értékgrafikon ábrázolása

1. Növekvő és csökkenő értékek pontjainak meghatározása. 2. Megszakítási pontok, szélsőségek és koordinátatengelyekkel való metszéspontok keresése. 3. A grafikonon a pozícióváltozások meghatározásának folyamata. 4. A konvexitás és konvexitás mutatójának és irányának meghatározása, figyelembe véve az aszimptoták jelenlétét. 5. Kutatási összefoglaló táblázat készítése koordinátáinak meghatározása szempontjából. 6. Növekvő és csökkenő szélső és éles pontok intervallumainak megtalálása. 7. Görbe domborúságának és konkávságának meghatározása. 8. A kutatást figyelembe vevő grafikon ábrázolása lehetővé teszi a minimum vagy maximum meghatározását.

A fő elem, amikor szélsőséges pontokkal kell dolgozni, a grafikonjának pontos felépítése. Az iskolai tanárok gyakran nem fordítanak maximális figyelmet egy ilyen fontos szempontra, amely az oktatási folyamat durva megsértését jelenti. A grafikon felépítése csak a funkcionális adatok tanulmányozása, az akut szélsőségek azonosítása, valamint a grafikon pontjai alapján történik. A derivált függvény éles szélsőértékei a pontos értékek diagramján jelennek meg, a segítségével szokásos eljárás az aszimptoták meghatározása. A függvény maximum és minimum pontjait több is kíséri összetett konstrukciók grafika. Ennek oka az akut extrémum problémájának mélyebb feldolgozásának szükségessége. Egy összetett és egyszerű függvény deriváltját is meg kell találni, hiszen ez az egyik legfontosabb fogalom az extrémum problémájában.

A funkcionális szélsősége

A fenti érték megtalálásához be kell tartania a következő szabályokat:

• meghatározza az extrém reláció szükséges feltételét;
• vegye figyelembe a grafikon szélső pontjainak megfelelő állapotát;
• végezze el az akut extrémum számítását.

Olyan fogalmakat is használnak, mint a gyenge minimum és az erős minimum. Ezt figyelembe kell venni az extrémum meghatározásakor és pontos kiszámításakor. Ugyanakkor az akut funkcionalitás a függvény grafikonjával való munkához szükséges összes feltétel keresése és létrehozása.

1. definíció. Az M(x 0 ; y 0) pontot a z = f(x; y) függvény maximális (minimális) pontjának nevezzük, ha az M pontnak olyan szomszédsága van, hogy ebből az összes (x; y) pontra szomszédságában a következő egyenlőtlenség érvényesül:

f(x 0 ; y 0)  f(x; y), .

1. tétel (az extrémum létezésének szükséges feltétele) . Ha egy z = f(x; y) differenciálható függvény extrémumot ér el az M(x 0 ; y 0) pontban, akkor elsőrendű parciális deriváltjai ebben a pontban nullával egyenlők, azaz.
;

Azokat a pontokat, ahol a parciális deriváltak egyenlők nullával, nevezzük helyhez kötött vagy kritikus pontok.

2. tétel (elegendő feltétel az extrémum meglétéhez)

Legyen z = f(x; y) függvény:

a) az (x 0 ; y 0) pont egy bizonyos környezetében definiált, amelyben
És
;

b) ezen a ponton folytonos másodrendű parciális deriváltjai vannak

;

Ekkor, ha  = AC  B 2 > 0, akkor az (x 0 ; y 0) pontban a z = f(x; y) függvénynek szélsőértéke van, és ha A< 0 (или С < 0) – максимум, если А >0 (vagy C > 0) – minimum.  = AC  B 2 esetben< 0, функция z = f(x; y) экстремума не имеет. Если  = AC  B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).

1. példa Határozzuk meg a z = x 2 + xy + y 2  3x  6y függvény szélsőértékét!

Megoldás. Keressük az elsőrendű parciális deriváltokat:

Használjuk az extrémum létezéséhez szükséges feltételt:

Az egyenletrendszert megoldva megtaláljuk a stacionárius pontok x és y koordinátáit: x = 0; y = 3, azaz M(0; 3).

Számítsuk ki a másodrendű parciális deriváltokat, és keressük meg értéküket az M pontban.

A =
= 2; C =
= 2;

B =
.

Tegyük fel a  = AC  B 2 = 2  2  1 > 0, A = 2 > 0 diszkriminánst. Ezért az M(0; 3) pontban az adott függvénynek van minimuma. A függvény értéke ezen a ponton z min = 9.

Keresse meg a függvények szélsőségeit

322. z = x 2 + y 2 + xy  4x  5y 323. z = y 3  x 3  3xy

324. z = x 2  2xy + 4y 3 325. z =
 y 2  x + 6y

326. z = x y (1  x  y) 327. z = 2xy  4x  2y

328. z = e  x/2 (x + y 2) 329. z = x 3 + 8y 3  6xy + 1

330. z = 3x 2 y  x 3  y 4 331. z = 3x + 6y  x 2  xy + y 2

Két változó függvényének legnagyobb és legkisebb értéke egy zárt tartományban

Annak érdekében, hogy megtalálja legnagyobbÉs legkevésbé egy függvény értékeit egy zárt régióban, akkor a következőket kell tennie:

1) keresse meg egy adott területen található kritikus pontokat, és számítsa ki ezeken a pontokon a függvényértékeket;

2) keresse meg a kritikus pontokat a régió határán, és számítsa ki a bennük lévő függvények legnagyobb és legkisebb értékét;

3) az összes talált érték közül válassza ki a legnagyobbat és a legkisebbet.

2. példa Keresse meg a z = függvény legnagyobb és legkisebb értékét
körben x 2 + y 2  1.

Megoldás. Keressük meg a vizsgált tartományon belül elhelyezkedő kritikus pontok koordinátáit, amelyekhez kiszámítjuk a z függvény elsőrendű parciális deriváltjait, és egyenlővé tesszük őket nullával.

ahol x = 0, y = 0, és ezért M(0; 0) kritikus pont.

Számítsuk ki a z függvény értékét az M(0; 0) pontban: z(0; 0) = 2.

Keressük meg a kritikus pontokat az x 2 + y 2 = 1 egyenlettel meghatározott kör tartomány határán. Ha y 2 = 1 - x 2-t behelyettesítünk a z = z(x; y) függvénybe, egy függvényt kapunk. egy változóból

z =
;

ahol x[1; 1].

A derivált kiszámítása után
és nullával egyenlővé téve kritikus pontokat kapunk az x 1 = 0, x 2 = tartomány határán. , x 3 =

Keressük meg a z(x) = függvény értékét
kritikus pontokon és a szakasz végein [1; 1]: z(0) = ;
=;
; z(1) = ; z(1) =

Válasszuk ki a z függvény értékei közül a legnagyobbat és a legkisebbet a kör belsejében és határán található kritikus pontokban.

Tehát z max. = z(0; 0) = 2

Az optimalizálási feladatokban szükség van a szélsőségek megtalálására két vagy több változó függvényei feltéve, hogy ennek a kapcsolatnak az egyenlet által adott változói között kapcsolat van . Ebben az esetben azt mondjuk, hogy meg kell találnunk feltételes szélsőség .

A feltételes szélsőség megtalálásához meg kell találnia részleges származékokés döntsön egyenletrendszerek Létezik egy algoritmus a feltételes szélsőség megtalálására három lépésben, amelyet most egy példa segítségével elemezünk, valamint a feltételes szélsőség geometriai jelentését, aminek el kell jutnia mindenkihez, ha éppen ezt a példát elemezzük.

Tehát elemezzük az algoritmust a leggyakoribb probléma - két változó függvényének feltételes szélsőértékének megtalálása - példáján. .

1. lépés. Bemutatott Lagrange funkció

ahol az első tag maga az eredeti függvény, a második mínusz előjelű tag pedig a kapcsolódási feltétel egyenletének bal oldala, megszorozva (lambda) - a Lagrange-szorzóval.

1. példa megtalálja feltételes szélsőségek két változó függvénye, amelyek egy téglalap területét az oldalaiban fejezik ki xÉs y feltéve, hogy van egy kötél, amely meg tudja kötni ezt a téglalapot, és ennek a kötélnek a hossza 100.

1. lépés. Megoldás. Hozzuk a kapcsolódási feltétel egyenletét a kívánt formába nullával a jobb oldalon:

.

Komponáljunk Lagrange funkció:

2. lépés. Egyenlőségekből egyenletrendszert állítunk össze részleges származékok nulla és a kapcsolódási feltétel egyenlete (a feltételes szélsőség létezésének szükséges jele):

Ennek az egyenletrendszernek a megoldásai egy lehetséges feltételes szélsőség pontjai - stacionárius pontok vagy, ahogy mondják, kritikus pontok.

1. példa 2. lépés.

Megoldás.

xÉs y :

Helyettesítsük be ezeket a kifejezéseket a harmadik egyenletbe, és keressük meg a Lagrange-szorzó értékét:

xÉs yés keresse meg az eredeti függvény változóinak értékeit:

Megkaptuk és. Ezek az értékek egyben az állópont koordinátái is. Így stacionárius pontot kaptunk.

3. lépés Legyen a 2. lépésben talált stacionárius pont. Annak meghatározásához, hogy a feltételes szélsőérték minimum vagy maximum, meg kell találni a Lagrange-függvény második differenciálját

és a kapott kifejezésben helyettesítse a „lambda” helyett annak értékeit (a Lagrange-szorzó értékeit), amelyeket a 2. lépésben találtunk.

Ha a Lagrange-függvény második differenciálértéke kisebb, mint nulla (), akkor az stacionárius pont egy maximumpont, ha nagyobb, mint nulla (), akkor az állópont egy minimumpont. Ha a Lagrange-függvény második differenciáljának értéke nulla, akkor további kutatások szükségesek, de az ilyen esetek gyakorlatilag nem fordulnak elő a hallgatókhoz rendelt feladatokban.

A stacionárius pontok koordinátáit behelyettesítjük a kezdőpontba, és így végül megtaláljuk feltételes szélsőségek (vagy minimum és maximum vagy e szélsőségek egyike).

1. példa 3. lépés.

Megoldás. Keressük meg a Lagrange-függvény második differenciálját:

Esetünkben, mivel az első és a harmadik komponens nulla, nem kell behelyettesítenünk a Lagrange-szorzó értékeit. De meg kell találni a kapcsolatot a különbségek között dxÉs dy :

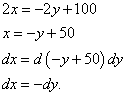
Mivel a kapott értékek ellentétes előjelűek, úgy találjuk, hogy minden esetben .

Most megtaláljuk az értéket feltételes véglet az eredeti függvényből, ami a maximum:

.

Ez az eredeti függvény által megadott téglalap maximális területe, amelyet egy 100 hosszú kötél korlátozhat.

2. példa megtalálja feltételes szélsőségek

1. lépés. Komponáljunk Lagrange funkció:

2. lépés. Keressük meg a Lagrange-függvény parciális deriváltjait, és alkossunk egyenletrendszert azok nullához való egyenlőségéből és a kapcsolódási feltétel egyenletéből:

Az első és a második egyenletből rendre kifejezzük xÉs y :

Helyettesítsük be ezeket a kifejezéseket a harmadik egyenletbe, és keressük meg a Lagrange-szorzó értékeit:

Helyettesítsük be most a Lagrange-szorzó értékét a kifejezésekbe xÉs yés keresse meg az eredeti függvény változóinak értékét a Lagrange-szorzó két értékéhez:

Ezek az x és y értékek két állópont koordinátái. Így stacionárius pontokat kaptunk .

3. lépés Keressük meg a Lagrange-függvény másodrendű parciális deriváltjait:

Keressük meg a Lagrange-függvény második differenciálját a képlet segítségével

:

Nullánál kisebb értéket kaptunk, ezért pont - pont feltételes maximum:

.

Állítsuk fel a Lagrange-függvény második differenciáljának előjelét a Lagrange-szorzó értékén:

Nullánál nagyobb értéket kaptunk, ezért pont - pont feltételes minimum:

.

És így, feltételes szélsőségek adott függvények találhatók.

3. példa megtalálja feltételes szélsőségek két változó függvényei .

1. lépés. Komponáljunk Lagrange funkció:

2. lépés. Keressük meg a Lagrange-függvény parciális deriváltjait, és alkossunk egyenletrendszert azok nullához való egyenlőségéből és a kapcsolódási feltétel egyenletéből:

Az első és a második egyenletből rendre kifejezzük xÉs y :

Azt tapasztaljuk azonban, hogy ha ezeket a változóértékeket behelyettesítjük a rendszer harmadik egyenletébe, nem adjuk meg a helyes egyenlőséget. Ezért úgy gondoljuk, hogy valójában az egyenlőség második tényezője egyenlő nullával: . Innentől kapunk

Stacionárius pontok koordinátáit keressük a Lagrange-szorzó értékén. Ekkor az egyenletrendszerből származó X és Y kifejezésekből az következik, hogy . A rendszer harmadik egyenletéből kapjuk.

A matematikában fontos fogalom a függvény. Segítségével vizuálisan elképzelheti a természetben előforduló számos folyamatot, és képletek, táblázatok és képek segítségével tükrözheti bizonyos mennyiségek közötti kapcsolatot. Példa erre a folyadékréteg nyomásának a testen való függése a merülés mélységétől, a gyorsulástól - egy bizonyos erő hatásától egy tárgyra, a hőmérséklet növekedésétől - az átvitt energiától és sok más folyamattól. Egy függvény tanulmányozása magában foglalja a gráf felépítését, tulajdonságainak, definíciós tartományának és értékeinek, növekedési és csökkenési intervallumainak megismerését. Egy fontos pont ez a folyamat az extrém pontok megtalálása. A továbbiakban arról fogunk beszélni, hogyan kell ezt helyesen megtenni.

Magáról a koncepcióról egy konkrét példa segítségével

Az orvostudományban a függvénygrafikon felrajzolása elárulhat egy betegség előrehaladását a páciens szervezetében, egyértelműen tükrözve az állapotát. Tegyük fel, hogy az OX tengely az időt jelenti napokban, az OU tengely pedig az emberi test hőmérsékletét. Az ábrán jól látható, hogy ez a mutató hogyan emelkedik meredeken, majd csökken. Könnyen észrevehető olyan speciális pontok is, amelyek tükrözik azokat a pillanatokat, amikor egy korábban növekvő függvény csökkenni kezd, és fordítva. Ezek szélsőséges pontok, vagyis kritikus értékek (maximum és minimum) a páciens hőmérsékletének ebben az esetben, ami után megváltozik az állapota.

Hajlásszög

Az ábráról könnyen megállapítható, hogyan változik a függvény deriváltja. Ha a grafikon egyenesei idővel felfelé mennek, akkor az pozitív. És minél meredekebbek, annál nagyobb a derivált értéke, ahogy a dőlésszög nő. A csökkenés időszakaiban ez az érték negatív értékeket vesz fel, a szélsőpontokban nullára fordul, és ez utóbbi esetben a derivált grafikonja párhuzamos az OX tengellyel.

Minden más folyamatot ugyanígy kell kezelni. De erről a koncepcióról a legjobb módja a különféle testek mozgása, amely jól látható a grafikonokon.

Mozgalom

Tegyük fel, hogy egy tárgy egyenes vonalban mozog, egyenletesen felveszi a sebességet. Ebben az időszakban a test koordinátáinak változását grafikusan egy bizonyos görbe ábrázolja, amelyet a matematikus a parabola ágának nevezne. Ugyanakkor a funkció folyamatosan növekszik, mivel a koordináta-jelzők másodpercenként gyorsabban és gyorsabban változnak. A sebesség grafikon a derivált viselkedését mutatja, melynek értéke is nő. Ez azt jelenti, hogy a mozgásnak nincsenek kritikus pontjai.

Ez a végtelenségig folytatódna. De mi van akkor, ha a test hirtelen úgy dönt, hogy lelassít, megáll és más irányba indul el? Ebben az esetben a koordináta mutatók csökkenni kezdenek. És a függvény átad egy kritikus értéket, és növekvőről csökkenőre vált.

Ezzel a példával ismét megértheti, hogy egy függvény grafikonján az extrémpontok azokban a pillanatokban jelennek meg, amikor a függvény megszűnik monoton lenni.

A származék fizikai jelentése

A korábban leírtak egyértelműen megmutatták, hogy a derivált lényegében a függvény változási sebessége. Ez a pontosítás tartalmazza annak fizikai jelentése. Az extrém pontok kritikus területek a grafikonon. Azonosíthatók és kimutathatók a derivált értékének kiszámításával, amely nullával egyenlő.

Van még egy jel, ami elégséges feltétele a szélsőségnek. Az ilyen inflexiós pontokon a derivált előjelét változtatja: „+”-ról „-”-ra a maximális területen, és „-”-ról „+”-ra a minimális területen.

Mozgás a gravitáció hatására

Képzeljünk el egy másik helyzetet. A labdával játszó gyerekek úgy dobták el, hogy az ferdén kezdett mozogni a látóhatárhoz képest. A kezdeti pillanatban ennek az objektumnak a sebessége volt a legnagyobb, de a gravitáció hatására csökkenni kezdett, és minden másodpercben ugyanannyival, körülbelül 9,8 m/s 2 -vel. Ez annak a gyorsulásnak az értéke, amely a föld gravitációjának hatására fellép a szabadesés során. A Holdon körülbelül hatszor kisebb lenne.

A test mozgását leíró grafikon egy parabola, melynek ágai lefelé mutatnak. Hogyan lehet megtalálni az extrém pontokat? Ebben az esetben ez a függvény teteje, ahol a test (labda) sebessége nulla értéket vesz fel. A függvény deriváltja nulla lesz. Ebben az esetben az irány, és így a sebességérték az ellenkezőjére változik. A test másodpercenként gyorsabban repül le, és ugyanannyit - 9,8 m/s 2 - gyorsul.

Második származék

Az előző esetben a sebességi modulus grafikonját egyenesként rajzoljuk meg. Ez a vonal kezdetben lefelé irányul, mivel ennek az értéknek az értéke folyamatosan csökken. Miután egy időpontban elérte a nullát, ennek az értéknek a mutatói növekedni kezdenek, és a sebességmodul grafikus ábrázolásának iránya drámaian megváltozik. A vonal most felfelé mutat.

A sebességnek, amely a koordináta időbeli deriváltja, szintén van egy kritikus pontja. Ebben a régióban a funkció kezdetben csökkenőben kezd növekedni. Ez a függvény deriváltjának szélsőpontjának helye. Ebben az esetben az érintő dőlésszöge nulla lesz. A gyorsulás pedig, amely a koordináta második deriváltja az idő függvényében, az előjelet „-”-ról „+”-ra változtatja. Az egyenletesen lassú mozgás pedig egyenletesen gyorsul.

Gyorsulási grafikon

Nézzünk most négy képet. Mindegyik egy olyan grafikont jelenít meg, amely az idő függvényében változik olyan fizikai mennyiségben, mint a gyorsulás. „A” esetén az értéke pozitív és állandó marad. Ez azt jelenti, hogy a test sebessége, akárcsak a koordinátája, folyamatosan növekszik. Ha azt képzeljük, hogy az objektum végtelenül sokáig fog így mozogni, akkor a koordináta időfüggőségét tükröző függvény folyamatosan növekszik. Ebből következik, hogy nincsenek kritikus területei. A derivált, azaz lineárisan változó sebesség grafikonján szintén nincsenek szélsőpontok.

Ugyanez vonatkozik a pozitív és folyamatosan növekvő gyorsulású „B” esetre is. Igaz, a koordináták és a sebesség grafikonjai itt valamivel bonyolultabbak lesznek.

Amikor a gyorsulás nullára megy

A „B” ábrát tekintve egészen más képet láthatunk, amely a test mozgását jellemzi. Sebességét grafikusan egy parabola ábrázolja lefelé irányuló ágakkal. Ha a gyorsulás változását leíró sort az OX tengellyel való metszésig folytatjuk és tovább, akkor elképzelhetjük, hogy e kritikus értékig, ahol a gyorsulás nullának bizonyul, a tárgy sebessége egyre lassabban fog növekedni. . A koordinátafüggvény deriváltjának szélsőpontja pontosan a parabola csúcsánál lesz, ezután a test gyökeresen megváltoztatja mozgásának természetét, és más irányba kezd el mozogni.

Az utolsó „G” esetben a mozgás jellege nem határozható meg pontosan. Itt csak azt tudjuk, hogy a vizsgált időszakban nincs gyorsulás. Ez azt jelenti, hogy a tárgy a helyén maradhat, vagy állandó sebességgel mozoghat.

Koordináta összeadás probléma

Térjünk át azokra a feladatokra, amelyekkel gyakran találkozunk az algebra iskolai tanulmányozása során, és amelyeket az egységes államvizsgára való felkészüléshez kínálnak. Az alábbi ábra a függvény grafikonját mutatja. Ki kell számítani a szélsőpontok összegét.

Tegyük ezt az ordináta tengelyre úgy, hogy meghatározzuk azon kritikus területek koordinátáit, ahol a függvény jellemzőiben változás figyelhető meg. Egyszerűen fogalmazva, megkeressük az OX tengely mentén az inflexiós pontok értékeit, majd folytassuk a kapott tagok hozzáadásával. A grafikon szerint nyilvánvaló, hogy a következő értékeket veszik fel: -8; -7 ; -5; -3; -2; 1; 3. Ez összeadja -21-et, ami a válasz.

Optimális megoldás

Nem kell magyarázni, milyen fontos lehet a megvalósítás gyakorlati feladatokat az optimális megoldás kiválasztása. Végül is sokféleképpen lehet elérni egy célt, de a legjobb kiút általában csak egy. Ez rendkívül szükséges például hajók, űrhajók és repülőgépek, valamint építészeti struktúrák tervezésekor, hogy megtalálják ezeknek az ember alkotta tárgyaknak az optimális formáját.

A járművek sebessége nagymértékben függ a vízen és levegőn áthaladva tapasztalható ellenállás megfelelő minimalizálásától, a gravitációs erők hatására fellépő túlterhelésektől és sok más mutatótól. A tengeren közlekedő hajónak olyan tulajdonságokra van szüksége, mint a stabilitás vihar alatt; a folyami hajóknál a minimális merülés fontos. Az optimális tervezés kiszámításakor a grafikon szélsőpontjai egyértelműen képet adnak arról a legjobb megoldásösszetett probléma. Az ilyen jellegű problémákat gyakran a közgazdaságtanban, az üzleti életben és sok más élethelyzetben oldják meg.

Az ókori történelemből

Még az ókori bölcseket is rendkívüli problémák foglalkoztatták. A görög tudósok matematikai számításokkal sikeresen megfejtették a területek és térfogatok titkát. Ők voltak az elsők, akik megértették, hogy különböző, azonos kerületű alakzatok síkján mindig a körnek van a legnagyobb területe. Hasonlóképpen, a labda a maximális térfogattal rendelkezik a térben lévő, azonos felületű objektumok között. Olyan híres személyiségek, mint Arkhimédész, Eukleidész, Arisztotelész, Apollonius szentelték magukat az ilyen problémák megoldásának. Heron kiválóan tudott extrém pontokat találni, és számítások segítségével zseniális eszközöket épített. Ilyenek voltak a gőzzel mozgó gépek, szivattyúk és azonos elven működő turbinák.

Karthágó építése

Van egy legenda, amelynek cselekménye az egyik szélsőséges probléma megoldásán alapul. A föníciai hercegnő üzleti megközelítésének eredménye, aki a bölcsekhez fordult segítségért, Karthágó megépítése volt. Ennek az ősi és híres városnak a telkét Didónak (ez volt az uralkodó neve) az egyik afrikai törzs vezetője adta. A kiosztás területe elsőre nem tűnt túl nagynak, hiszen a szerződés szerint ökörbőrrel kellett volna borítani. De a hercegnő megparancsolta katonáinak, hogy vágják vékony csíkokra, és készítsenek belőlük övet. Olyan hosszúnak bizonyult, hogy egy egész város elfért benne.

A matematikai elemzés eredete

Most térjünk át az ókorból egy későbbi korszakba. Érdekes, hogy Keplert a 17. században egy borárussal való találkozás késztette arra, hogy megértse a matematikai elemzés alapjait. A kereskedő annyira jártas volt a szakmájában, hogy egy vaskötelet leeresztve könnyedén meg tudta határozni a hordóban lévő ital térfogatát. Egy ilyen érdekességre gondolva a híres tudósnak sikerült megoldania ezt a dilemmát magának. Kiderült, hogy az akkori ügyes kádárok rájöttek az edénykészítésre úgy, hogy a rögzítőgyűrűk kerületének bizonyos magasságában és sugarában maximális kapacitással rendelkezzenek.

Ez okot adott Keplernek a továbbgondolásra. A kádárok hosszas keresgélés, hibák és újabb próbálkozások során jutottak el az optimális megoldáshoz, tapasztalataikat generációról generációra adva. De Kepler fel akarta gyorsítani a folyamatot, és megtanulni, hogyan kell rövid időn belül matematikai számításokkal megtenni ugyanezt. Minden fejlesztése, amelyet kollégái átvettek, a ma már híres Fermat- és Newton-Leibniz-tételekké változott.

Maximális terület probléma

Képzeljük el, hogy van egy huzalunk, melynek hossza 50 cm. Hogyan készítsünk belőle olyan téglalapot, amelynek a területe a legnagyobb?

A döntés megkezdésekor a mindenki által ismert egyszerű igazságokból kell kiindulnia. Jól látható, hogy a figuránk kerülete 50 cm lesz, mindkét oldala dupla hosszából áll. Ez azt jelenti, hogy ha az egyiket „X”-nek jelöltük, a másikat (25 - X) lehet kifejezni.

Innen egy X(25 - X) területet kapunk. Ez a kifejezés olyan függvénynek tekinthető, amely több értéket vesz fel. A probléma megoldásához meg kell találni belőlük a maximumot, ami azt jelenti, hogy meg kell találni az extrém pontokat.

Ehhez megkeressük az első deriváltot, és egyenlővé tesszük nullával. Az eredmény egy egyszerű egyenlet: 25 - 2X = 0.

Ebből megtudjuk, hogy az egyik oldal X = 12,5.

Ezért a másik: 25 - 12,5 = 12,5.

Kiderült, hogy a probléma megoldása egy 12,5 cm-es oldalú négyzet lesz.

Hogyan lehet megtalálni a maximális sebességet

Nézzünk egy másik példát. Képzeljük el, hogy van egy test, egyenes vonalú mozgás amelyet az S = - t 3 + 9t 2 - 24t - 8 egyenlet ír le, ahol a megtett távolság méterben, az idő pedig másodpercben van kifejezve. Meg kell találnunk a maximális sebességet. Hogyan kell csinálni? Letöltve megtaláljuk a sebességet, vagyis az első deriváltot.

A következő egyenletet kapjuk: V = - 3t 2 + 18t - 24. A feladat megoldásához ismét meg kell találnunk a szélsőpontokat. Ezt ugyanúgy kell elvégezni, mint az előző feladatnál. Megtaláljuk a sebesség első deriváltját, és egyenlővé tesszük nullával.

A következőt kapjuk: - 6t + 18 = 0. Ebből t = 3 s. Ez az az idő, amikor a test sebessége kritikus értéket vesz fel. A kapott adatokat behelyettesítjük a sebességegyenletbe, és megkapjuk: V = 3 m/s.

De hogyan érti, mi az? maximális sebesség, mert egy függvény kritikus pontjai lehetnek a legnagyobb vagy legkisebb értékei? Az ellenőrzéshez meg kell találnia a sebesség második deriváltját. Ezt a 6-os szám mínuszjellel fejezi ki. Ez azt jelenti, hogy a talált pont maximum. És abban az esetben pozitív érték a második derivált minimum lenne. Ez azt jelenti, hogy a talált megoldás helyesnek bizonyult.

A példaként felhozott feladatok csak egy része azoknak, amelyek megoldhatók, ha tudjuk, hogyan találjuk meg egy függvény szélsőpontjait. Sőt, sokkal több van belőlük. Az ilyen tudás pedig korlátlan lehetőségeket nyit meg az emberi civilizáció előtt.

Funkció y = f(x)-t hívjuk növekvő (csökkenő) egy bizonyos intervallumban, ha x 1-re< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).

Ha az y = f (x) differenciálható függvény növekszik (csökken) egy intervallumon, akkor a deriváltja ezen az f intervallumon " (x)> 0

(f"(x)< 0).

Pont x O hívott helyi maximum pont (minimális) f (x) függvény, ha van a pont szomszédsága x o, amelynek minden pontjára igaz az f (x) egyenlőtlenség≤ f (x o ) (f (x )≥ f (x o )).

A maximum és minimum pontokat hívjuk szélsőséges pontok, és a függvény értékei ezeken a pontokon az ő szélsőségek.

Extrém pontok

A szükséges feltételek extrémum . Ha a lényeg x O az f (x) függvény szélsőpontja, akkor vagy f " (x o ) = 0 vagy f(x o ) nem létezik. Az ilyen pontokat ún kritikai, maga a függvény pedig a kritikus pontban van definiálva. Egy függvény szélsőpontját a kritikus pontjai között kell keresni.

Az első elégséges feltétel. Hadd x O - kritikus pont. Ha f" (x ) ponton való áthaladáskor x O módosítja a plusz jelet mínuszra, majd a pontra x o a függvénynek van maximuma, egyébként minimuma. Ha a kritikus ponton áthaladva a derivált nem vált előjelet, akkor a pontban x O nincs szélsőség.

Második elégséges feltétel. Legyen az f(x) függvény
f" (x ) pont közelében x O és a második derivált f "" (x 0) magában a pontban x o. Ha f"(x o) = 0, f "" (x 0)>0 (f "" (x 0)<0), то точка x o az f (x) függvény lokális minimum (maximum) pontja. Ha f "" (x 0) = 0, akkor vagy az első elégséges feltételt kell használnia, vagy magasabbakat kell bevonnia.

Egy szakaszon az y = f (x) függvény akár a kritikus pontokon, akár a szakasz végein elérheti minimális vagy maximum értékét.

Példa 3.22.

Megoldás. Mert f " (

Egy függvény szélsőértékének megtalálásának problémái

3.23. példa. a

Megoldás. xÉs y y
0 ≤ x≤
> 0, és mikor x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение funkciókat kv. egységek).

3.24. példa. p ≈

Megoldás. p o
S"
R=2, H=16/4=4.

Példa 3.22.Határozzuk meg az f (x) = 2x 3 - 15x 2 + 36x - 14 függvény szélsőértékét.

Megoldás. Mert f " (x ) = 6x 2 - 30x +36 = 6(x ​​-2)(x - 3), akkor az x 1 = 2 és x 2 = 3 függvény kritikus pontjai. Extréma csak ezeken a pontokon lehet. Mivel az x 1 = 2 ponton áthaladva a derivált előjelét pluszból mínuszba változtatja, akkor ezen a ponton a függvénynek van maximuma. Az x 2 = 3 ponton áthaladva a derivált az előjelét mínuszról pluszra változtatja, így az x 2 = 3 pontban a függvénynek minimuma van. A pontokban a függvényértékek kiszámítása után
x 1 = 2 és x 2 = 3, akkor megtaláljuk a függvény szélsőértékét: maximum f (2) = 14 és minimum f (3) = 13.

3.23. példa.A kőfal közelében téglalap alakú területet kell építeni úgy, hogy három oldalról dróthálóval legyen elkerítve, a negyedik oldal pedig a fal mellett legyen. Erre van a lineáris méteres háló. Milyen képarány mellett lesz a webhely legnagyobb területe?

Megoldás.Jelöljük az emelvény oldalait -vel xÉs y. A telek területe S = xy. Hadd y- ez a fal melletti oldal hossza. Ekkor feltétel szerint teljesülnie kell a 2x + y = a egyenlőségnek. Ezért y = a - 2x és S = x (a - 2x), ahol
0 ≤ x≤ a /2 (a terület hossza és szélessége nem lehet negatív). S " = a - 4x, a - 4x = 0 x = a/4-nél, innen
y = a - 2 × a/4 =a/2. Mert a x = a /4 az egyetlen kritikus pont, nézzük meg, hogy ezen a ponton áthaladva változik-e a derivált előjele. x a /4 S "> 0, és mikor x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение funkciókat S(a/4) = a/4(a - a/2) = a 2 /8 (kv. egységek). Mivel S folyamatos bekapcsolt állapotban van, és értékei az S(0) és S(a /2) végén egyenlők nullával, akkor a talált érték lesz a függvény legnagyobb értéke. Így a lelőhely legkedvezőbb oldalaránya a feladat adott feltételei mellett y = 2x.

3.24. példa.V=16 űrtartalmú zárt hengeres tartály gyártása szükséges p ≈ 50 m 3. Mekkora legyen a tartály mérete (R sugár és H magasság), hogy a gyártáshoz a legkevesebb anyag kerüljön felhasználásra?

Megoldás.A henger teljes felülete S = 2 p R(R+H). Ismerjük a henger térfogatát V = p R 2 Н Þ Н = V/ p R 2 =16 p / p R2 = 16/R2. Tehát S(R) = 2 p (R 2 +16/R). Megtaláljuk ennek a függvénynek a származékát:
S"(R) = 2 p (2R-16/R2) = 4 p (R-8/R2). S" (R) = 0, ha R3 = 8, ezért
R=2, H=16/4=4.