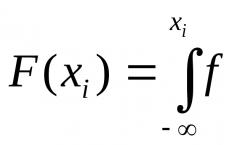Metoda inverzne funkcije

Naj bo zahtevano predvajanje zvezne naključne spremenljivke X, tj. pridobite zaporedje njegovih možnih vrednosti x jaz (jaz= 1,2, ...), poznavanje distribucijske funkcije F(X).

Izrek. če r jaz ,-naključno število, nato možna vrednostx jaz zvezna naključna spremenljivka X, ki se igra z dano porazdelitveno funkcijoF(X)ustreznar jaz , je koren enačbe

F(X jaz)= r jaz . (»)

Dokaz. Naj bo izbrano naključno število r jaz (0≤r jaz <1). Так как в интервале всех возможных зна­чений X distribucijska funkcija F(X) monotono narašča od 0 do 1, potem v tem intervalu obstaja in samo ena taka vrednost argumenta X jaz , pri kateri distribucijska funkcija dobi vrednost r jaz. Z drugimi besedami, enačba (*) ima edinstveno rešitev

X jaz = F - 1 (r jaz),

Kje F - 1 - inverzna funkcija y=F(X).

Dokažimo zdaj, da je koren X jaz enačba (*) je možna vrednost takšne zvezne naključne spremenljivke (začasno jo bomo označili z ξ , nato pa se prepričajte, da ξ=X). V ta namen dokažemo, da je verjetnost zadetka ξ v interval, na primer ( z,d), ki pripadajo intervalu vseh možnih vrednosti X, je enaka prirastku porazdelitvene funkcije F(X) v tem intervalu:

R(z< ξ < d)= F(d)- F(z).

Dejansko, saj F(X)- monotono naraščajočo funkcijo v intervalu vseh možnih vrednosti x, potem v tem intervalu velike vrednosti argumenta ustrezajo velikim vrednostim funkcije in obratno. Zato, če z <X jaz < d, To F(c)< r jaz < F(d), in obratno [ob upoštevanju, da zaradi (*) F(X jaz)=r jaz ].

Iz teh neenakosti sledi, da če je naključna spremenljivka ξ zaprt v intervalu

z< ξ < d, ξ (**)

nato naključna spremenljivka R zaprt v intervalu

F(z)< R< F(d), (***)

in nazaj. Tako sta neenakosti (**) in (***) enakovredni in zato enako verjetni:

R(z< ξ< d)=P[F(z)< R< F(d)]. (****)

Od vrednosti R enakomerno porazdeljena v intervalu (0,1), nato pa verjetnost zadetka R nekemu intervalu, ki pripada intervalu (0,1), je enaka njegovi dolžini (glej XI. poglavje, § 6, opomba). Še posebej,

R[F(z)< R< F(d) ] = F(d) - F(z).

Zato lahko relacijo (****) zapišemo kot

R(z< ξ< d)= F(d) - F(z).

Torej verjetnost zadetka ξ v interval ( z,d) je enaka prirastku porazdelitvene funkcije F(X) na tem intervalu, kar pomeni, da ξ=X. Z drugimi besedami, številke X jaz, definirana s formulo (*), so možne vrednosti količine X s dana distribucijska funkcija F(X), Q.E.D.

1. praviloX jaz , zvezna naključna spremenljivka x, poznavanje njegove distribucijske funkcije F(X), morate izbrati naključno število r jaz enačajte njene porazdelitvene funkcije in rešite X jaz , nastala enačba

F(X jaz)= r jaz .

Opomba 1. Če te enačbe ni mogoče eksplicitno rešiti, se zatečemo k grafični ali numerični metodi.

Primer I Igrajte 3 možne vrednosti zvezne naključne spremenljivke x, enakomerno porazdeljena v intervalu (2, 10).

rešitev. Zapišimo porazdelitveno funkcijo količine x, enakomerno porazdeljena v intervalu ( A,b) (glej primer poglavja XI, § 3):

F(X)= (ha)/ (b-A).

Po pogoju, a = 2, b=10, torej

F(X)= (X- 2)/ 8.

S pravilom iz tega razdelka napišemo enačbo za iskanje možnih vrednosti X jaz , za katero porazdelitveno funkcijo enačimo z naključnim številom:

(X jaz -2 )/8= r jaz .

Od tod X jaz =8 r jaz + 2.

Izberimo 3 naključne številke, npr. r jaz =0,11, r jaz =0,17, r jaz=0,66. Te številke zamenjajte v enačbo, razrešeno glede na X jaz , kot rezultat dobimo ustrezne možne vrednosti X: X 1 \u003d 8 0,11 + 2 \u003d\u003d 2,88; X 2 =1.36; X 3 = 7,28.

Primer 2 Zvezna naključna spremenljivka X porazdeljena po eksponentnem zakonu, ki ga poda porazdelitvena funkcija (parameter λ > 0 je znan)

F(X)= 1 - e - λ X (x>0).

Potrebno je najti eksplicitno formulo za igranje možnih vrednosti x.

rešitev. S pomočjo pravila tega odstavka zapišemo enačbo

1 - e - λ X jaz

Rešimo to enačbo za X jaz :

e - λ X jaz = 1 - r jaz, oz - λ X jaz = ln(1 - r jaz).

X jaz =1p(1– r jaz)/λ .

Naključno število r jaz v intervalu (0,1); torej številka 1 - r jaz, prav tako naključen in spada v interval (0,1). Z drugimi besedami, količine R in 1- R enakomerno porazdeljena. Zato, da bi našli X jaz Uporabite lahko preprostejšo formulo:

x jaz =- ln r jaz /λ.

Opomba 2. Znano je, da (glej poglavje XI, §3)

Še posebej,

Iz tega sledi, da če je gostota verjetnosti znana f(x), nato za igranje X namesto enačb F(x jaz)=r jaz odloča o x jaz enačba

2. pravilo Da bi našli možno vrednost X jaz (zvezna naključna spremenljivka x, poznavanje njegove gostote verjetnosti f(x) izberite naključno število r jaz in se odloči za X jaz , enačba

ali enačba

Kje A- najmanjša končna možna vrednost x.

Primer 3 Glede na gostoto verjetnosti zvezne naključne spremenljivke Xf(X)=λ (1-λx/2) v intervalu (0; 2/λ); zunaj tega intervala f(X)= 0. Potrebno je najti eksplicitno formulo za igranje možnih vrednosti x.

rešitev. Enačbo zapišemo v skladu s pravilom 2

Po integraciji in rešitvi dobljene kvadratne enačbe za X jaz, končno dobimo

LABORATORIJSKO DELO MM-03

PREDVAJANJE DISKRETNIH IN NEPREKIDNIH ROV

Namen dela: študij in programska implementacija metod za predvajanje diskretnih in neprekinjenih RV

VPRAŠANJA ZA PREUČITEV IZ POVZETKA PREDAVANJA:

1. Diskretne naključne spremenljivke in njihove značilnosti.

2. Predvajanje celotne skupine naključnih dogodkov.

3. Predvajanje zvezne naključne spremenljivke z metodo inverzne funkcije.

4. Izbira naključne smeri v prostoru.

5. Standardna normalna porazdelitev in njen preračun za podane parametre.

6. Metoda polarnih koordinat za igranje normalne porazdelitve.

NALOGA 1. Oblikujte (pisno) pravilo za igranje vrednosti diskretnega RV, katerega distribucijski zakon je podan v obliki tabele. Sestavite funkcijo podprograma za predvajanje vrednosti CV z uporabo BSV, prejetega iz podprograma RNG. Predvajajte 50 vrednosti CB in jih prikažite na zaslonu.

Kjer je N številka različice.

NALOGA 2. Podana je funkcija gostote porazdelitve f(x) zvezne naključne spremenljivke X.

V poročilo zapišite formule in izračun naslednjih vrednosti:

A) normalizacijska konstanta;

B) porazdelitvena funkcija F(x);

C) matematično pričakovanje M(X);

D) disperzija D(X);

E) formula za igranje vrednosti CB z metodo inverzne funkcije.

Sestavite funkcijski podprogram za predvajanje podanega življenjepisa in pridobite 1000 vrednosti tega življenjepisa.

Sestavite histogram porazdelitve dobljenih števil na 20 segmentov.

NALOGA 3. Napišite postopek, ki vam omogoča predvajanje parametrov naključne smeri v prostoru. Igrajte 100 naključnih smeri v prostoru.

Uporabite vgrajeni generator psevdonaključnih števil.

Pisno poročilo o laboratorijskem delu naj vsebuje:

1) naziv in namen dela, skupina, priimek in številka izbire študenta;

2) Za vsako nalogo: -pogoj, -potrebne formule in matematične transformacije, -ime programske datoteke, ki implementira uporabljeni algoritem, -rezultati izračuna.

Odpravljene programske datoteke se predajo skupaj s pisnim poročilom.

UPORABA

Različice gostote porazdelitve zveznega SW

Var-t	SW gostota porazdelitve	Var-t	SW gostota porazdelitve

Bistvo metode Monte Carlo je naslednje: najti morate vrednost A neka preučevana vrednost. V ta namen se izbere taka naključna spremenljivka X, katere matematično pričakovanje je enako a: M(X)=a.

V praksi delajo to: izračunajo (izigrajo) n možne vrednosti x i naključne spremenljivke X, poiščite njihovo aritmetično sredino

In vzamejo kot oceno (približno vrednost) a * želenega števila a. Tako je za uporabo metode Monte Carlo potrebno znati igrati naključno spremenljivko.

Naj bo zahtevano predvajanje diskretne naključne spremenljivke X, tj. izračunajte zaporedje njegovih možnih vrednosti x i (i=1,2, …) ob poznavanju porazdelitvenega zakona X. Uvedemo zapis: R je zvezna naključna spremenljivka, enakomerno porazdeljena v intervalu (0,1); r i (j=1,2,…) – naključna števila (možne vrednosti R).

Pravilo: Za predvajanje diskretne naključne spremenljivke X, ki jo določa distribucijski zakon

X x 1 x 2 ... x n

P p 1 p 2 … p n

1. Razdelite interval (0,1) osi ali na n delnih intervalov:

Δ 1 = (0; p 1), Δ 2 = (p 1; p 1+ p 2), ..., Δ n = (p 1 + p 2 + ... + p n -1; 1).

2. Izberite naključno število r j . Če je r j padel v delni interval Δ i, je igralna vrednost imela možno vrednost x i. .

Predvajanje celotne skupine dogodkov

Potrebno je odigrati teste, v vsakem od katerih se zgodi eden od dogodkov celotne skupine, katerih verjetnosti so znane. Predvajanje celotne skupine dogodkov je zmanjšano na predvajanje diskretne naključne spremenljivke.

Pravilo: Za igranje testov, v vsakem od katerih se zgodi eden od dogodkov A 1, A 2, ..., A n celotne skupine, katerih verjetnosti so znane p 1, p 2, ..., p n, dovolj je igrati diskretno vrednost X z naslednjim zakonom porazdelitve:

P p 1 p 2 … p n

Če je pri testu vrednost X prevzela možno vrednost x i =i, se je zgodil dogodek A i.

Predvajanje zvezne naključne spremenljivke

Znana je porazdelitvena funkcija F zvezne naključne spremenljivke X. Zahtevano je predvajanje X, tj. izračunajte zaporedje možnih vrednosti x i (i=1,2, …).

A. Metoda inverznih funkcij. 1. pravilo x i zvezne naključne spremenljivke X, če poznate njeno porazdelitveno funkcijo F, morate izbrati naključno število r i , izenačiti njeno porazdelitveno funkcijo in rešiti za x i nastalo enačbo F(х i) = r i .

Če je gostota verjetnosti f(x) znana, se uporabi pravilo 2.

2. pravilo Zaigrati možen pomen x i zvezne naključne spremenljivke X, če poznate njeno gostoto verjetnosti f, morate izbrati naključno število r i in rešiti enačbo za x i

ali enačba

kjer je a najmanjša končna možna vrednost X.

B. Metoda superpozicije. 3. pravilo Za predvajanje možne vrednosti naključne spremenljivke X, katere distribucijska funkcija

F(x) = C 1 F 1 (x)+C 2 F 2 (x)+…+C n F n (x),

kjer F k (x) – porazdelitvene funkcije (k=1, 2, …, n), С k >0, С i +С 2 +…+С n =1, je treba izbrati dve neodvisni naključni števili r 1 in r 2 ter za naključno število r 1 odigrajte možno vrednost pomožne diskretne naključne spremenljivke Z (v skladu s pravilom 1):

p C 1 C 2 … C n

Če se izkaže, da je Z=k, potem je enačba F k (x) = r 2 rešena za x.

Opomba 1. Če je gostota verjetnosti zvezne naključne spremenljivke X podana v obliki

f(x)=C 1 f 1 (x)+C 2 f 2 (x)+…+C n f n (x),

kjer so f k gostote verjetnosti, koeficienti C k so pozitivni, njihova vsota je enaka ena, in če se izkaže, da je Z=k, potem rešujejo (v skladu s pravilom 2) glede na x i glede na ali enačbo

Približno igranje normalne naključne spremenljivke

Pravilo. Da bi približno ocenili možno vrednost x i normalne naključne spremenljivke X s parametroma a=0 in σ=1, prištejte 12 neodvisnih naključnih števil in dobljeni vsoti odštejte 6:

Komentiraj. Če želite približno igrati normalno naključno spremenljivko Z z matematičnim pričakovanjem A in standardno deviacijo σ, nato pa po predvajanju možne vrednosti x i v skladu z zgornjim pravilom najdejo želeno možno vrednost po formuli: z i =σx i +a.

Opredelitev 24.1.naključna števila poimenovati možne vrednosti r zvezna naključna spremenljivka R, enakomerno porazdeljena v intervalu (0; 1).

1. Predvajanje diskretne naključne spremenljivke.

Naj bo zahtevano predvajanje diskretne naključne spremenljivke X, to je pridobiti zaporedje njegovih možnih vrednosti ob poznavanju distribucijskega zakona X:

x x 1 X 2 … x n

p str 1 R 2 … r str .

Razmislite o naključni spremenljivki, enakomerno porazdeljeni v (0, 1) R in razdeli interval (0, 1) na točke s koordinatami R 1, R 1 + R 2 , …, R 1 + R 2 +… +r str-1 vključeno p delni intervali, katerih dolžine so enake verjetnosti z enakimi indeksi.

Izrek 24.1.Če je vsakemu naključnemu številu, ki pade v interval, dodeljena možna vrednost, bo igralna vrednost imela dani zakon porazdelitve:

x x 1 X 2 … x n

p str 1 R 2 … r str .

Dokaz.

Možne vrednosti dobljene naključne spremenljivke sovpadajo z nizom X 1 , X 2 ,… x n, saj je število intervalov p, in ko je zadet r j v intervalu lahko naključna spremenljivka zavzame le eno od vrednosti X 1 , X 2 ,… x n.

Ker R je enakomerno porazdeljen, potem je verjetnost, da pade v vsak interval, enaka njegovi dolžini, kar pomeni, da vsaka vrednost ustreza verjetnosti pi. Tako ima naključna spremenljivka, ki se igra, dano distribucijsko zakonodajo.

Primer. Predvajajte 10 vrednosti diskretne naključne spremenljivke X, katerega porazdelitveni zakon ima obliko: X 2 3 6 8

R 0,1 0,3 0,5 0,1

rešitev. Interval (0, 1) razdelimo na delne intervale: D 1 - (0; 0,1), D 2 - (0,1; 0,4), D 3 - (0,4; 0,9), D 4 - (0,9; 1). Iz tabele naključnih števil izpišimo 10 števil: 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0,34. Prvo in sedmo število ležita na intervalu D 1, zato je v teh primerih naključna spremenljivka, ki se igra, dobila vrednost X 1 = 2; tretje, četrto, osmo in deseto število so padle v interval D 2 , kar ustreza X 2 = 3; druga, peta, šesta in deveta številka so bile v intervalu D 3 - medtem ko X = x 3 = 6; niti ena številka ni padla v zadnji interval. Torej, odigrane možne vrednosti X so: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. Igranje nasprotnih dogodkov.

Naj bo potrebno igrati poskuse, v vsakem od njih dogodek A pojavi z znano verjetnostjo R. Razmislite o diskretni naključni spremenljivki X, ki ima vrednosti 1 (če dogodek A zgodilo) z verjetnostjo R in 0 (če A ni zgodilo) z verjetnostjo q = 1 – str. Nato odigramo to naključno spremenljivko, kot je predlagano v prejšnjem odstavku.

Primer. Igrajte 10 izzivov, vsak z dogodkom A pojavi z verjetnostjo 0,3.

rešitev. Za naključno spremenljivko X z distribucijskim zakonom X 1 0

R 0,3 0,7

dobimo intervala D 1 - (0; 0,3) in D 2 - (0,3; 1). Uporabimo enak vzorec naključnih števil kot v prejšnjem primeru, pri katerem številke №№1,3 in 7 spadajo v interval D 1, ostale pa v interval D 2 . Zato lahko domnevamo, da dogodek A zgodilo v prvem, tretjem in sedmem poskusu, vendar se ni zgodilo v drugih.

3. Predvajanje celotne skupine dogodkov.

Če dogodki A 1 , A 2 , …, A str, katerih verjetnosti so enake R 1 , R 2 ,… r str, tvorite popolno skupino, potem lahko za predvajanje (to je modeliranje zaporedja njihovih nastopov v nizu testov) predvajate diskretno naključno spremenljivko X z distribucijskim zakonom X 1 2 … P, to storite na enak način kot v odstavku 1. Hkrati predpostavljamo, da

p str 1 R 2 … r str

če X prevzame vrednost x i = i, potem se je v tem poskusu zgodil dogodek A i.

4. Predvajanje zvezne naključne spremenljivke.

a) Metoda inverznih funkcij.

Naj bo zahtevano predvajanje zvezne naključne spremenljivke X, tj. pridobite zaporedje njegovih možnih vrednosti x i (jaz = 1, 2, …, n), poznavanje distribucijske funkcije F(x).

Izrek 24.2.če r i je naključno število, nato možna vrednost x i predvajana zvezna naključna spremenljivka X z dano distribucijsko funkcijo F(x), ki ustreza r i, je koren enačbe

F(x i) = r i. (24.1)

Dokaz.

Ker F(x) monotono narašča v območju od 0 do 1, potem obstaja (in edinstvena) vrednost argumenta x i, pri kateri distribucijska funkcija prevzame vrednost r i. Zato ima enačba (24.1) edinstveno rešitev: x i= F -1 (r i), Kje F-1 - funkcija inverzna na F. Dokažimo, da je koren enačbe (24.1) možna vrednost obravnavane naključne spremenljivke X. Recimo najprej to x i je možna vrednost neke naključne spremenljivke x in dokažemo, da je verjetnost, da x pade v interval ( c, d) je enako F(d) – F(c). Dejansko zaradi monotonosti F(x) in to F(x i) = r i. Potem

Zato je verjetnost, da x pade v interval ( c, d) je enaka prirastku porazdelitvene funkcije F(x) na tem intervalu, torej x = X.

Igrajte 3 možne vrednosti zvezne naključne spremenljivke X, enakomerno porazdeljena v intervalu (5; 8).

F(x) = , to pomeni, da je treba rešiti enačbo. Izberimo 3 naključna števila: 0,23; 0,09 in 0,56 in ju nadomestite v to enačbo. Pridobite ustrezne možne vrednosti X:

b) Metoda superpozicije.

Če je porazdelitveno funkcijo naključne spremenljivke, ki se predvaja, mogoče predstaviti kot linearno kombinacijo dveh porazdelitvenih funkcij:

potem , ker pri X®¥ F(x) ® 1.

Uvedemo pomožno diskretno naključno spremenljivko Z z distribucijskim zakonom

Z 12. Izberimo 2 neodvisni naključni števili r 1 in r 2 in odigrajte možno

pc 1 C 2

pomen Z po številki r 1 (glej odstavek 1). če Z= 1, potem iščemo želeno možno vrednost X iz enačbe, in če Z= 2, potem rešimo enačbo .

Lahko se dokaže, da je v tem primeru porazdelitvena funkcija naključne spremenljivke, ki se igra, enaka dani porazdelitveni funkciji.

c) Približna simulacija normalne naključne spremenljivke.

Ker za R, enakomerno porazdeljen v (0, 1), , potem za vsoto p neodvisne, enakomerno porazdeljene v intervalu (0,1) naključne spremenljivke . Nato je na podlagi centralnega limitnega izreka normalizirana naključna spremenljivka pri p® ¥ bo imel porazdelitev blizu normalne s parametri A= 0 in s =1. Zlasti je dobljen dokaj dober približek za p = 12:

Torej, za predvajanje možne vrednosti normalizirane normalne naključne spremenljivke X, morate dodati 12 neodvisnih naključnih števil in od vsote odšteti 6.

Pošljite svoje dobro delo v bazo znanja je preprosto. Uporabite spodnji obrazec

Študenti, podiplomski študenti, mladi znanstveniki, ki bazo znanja uporabljajo pri študiju in delu, vam bodo zelo hvaležni.

Gostuje na http://www.allbest.ru/

AKTIVNOST 1

Simulacija naključnih dogodkov z danim porazdelitvenim zakonom

Predvajanje diskretne naključne spremenljivke

Naj bo zahtevano predvajanje diskretne naključne spremenljivke, tj. dobimo zaporedje njegovih možnih vrednosti x i (i = 1,2,3,...n), poznamo distribucijski zakon X:

Z R označimo zvezno naključno spremenljivko. Vrednost R je enakomerno porazdeljena v intervalu (0,1). Z r j (j = 1,2,...) označimo možne vrednosti naključne spremenljivke R. Razdelimo interval 0< R < 1 на оси 0r точками с координатами на n частичных интервалов.

Potem dobimo:

Vidimo, da je dolžina delnega intervala z indeksom i enaka verjetnosti R z enakim indeksom. Dolžina

Ko torej naključno število r i pade v interval, prevzame naključna spremenljivka X vrednost x i z verjetnostjo P i .

Obstaja naslednji izrek:

Če je vsakemu naključnemu številu, ki je padlo v interval, dodeljena možna vrednost x i , bo igralna vrednost imela dani zakon porazdelitve

Algoritem za igranje diskretne naključne spremenljivke, podane z distribucijskim zakonom

1. Interval (0,1) osi 0r je potrebno razbiti na n delnih intervalov:

2. Izberite (na primer iz tabele naključnih števil ali v računalniku) naključno število r j .

Če je r j padel v interval, je diskretna naključna spremenljivka, ki se predvaja, prevzela možno vrednost x i .

Predvajanje zvezne naključne spremenljivke

Naj se zahteva predvajanje zvezne naključne spremenljivke X, tj. dobite zaporedje njegovih možnih vrednosti x i (i = 1,2,...). V tem primeru je porazdelitvena funkcija F(X) znana.

obstaja Naslednji izrek.

Če je r i naključno število, potem je možna vrednost x i predvajane zvezne naključne spremenljivke X z znano porazdelitveno funkcijo F(X), ki ustreza r i, koren enačbe.

Algoritem za predvajanje zvezne naključne spremenljivke:

1. Izbrati je treba naključno število r i .

2. Izenačimo izbrano naključno število znane porazdelitvene funkcije F(X) in dobimo enačbo.

3. Reši to enačbo za x i . Dobljena vrednost x i bo istočasno ustrezala naključnemu številu r i . in podan distribucijski zakon F(X).

Primer. Predvajajte 3 možne vrednosti zvezne naključne spremenljivke X, enakomerno porazdeljene v intervalu (2; 10).

Porazdelitvena funkcija X ima naslednjo obliko:

Po pogoju je a = 2, b = 10, torej

V skladu z algoritmom za igranje zvezne naključne spremenljivke enačimo F(X) z izbranim naključnim številom r i .. Iz tega dobimo:

Zamenjajte te številke v enačbo (5.3). Dobimo ustrezne možne vrednosti x:

Problemi modeliranja naključnih dogodkov z danim porazdelitvenim zakonom

1. Predvajati je potrebno 10 vrednosti diskretne naključne spremenljivke, tj. dobimo zaporedje njegovih možnih vrednosti x i (i=1,2,3,…n), poznamo distribucijski zakon X

Iz tabele naključnih števil izberimo naključno število r j: 0,10; 0,12; 0,37; 0,09; 0,65; 0,66; 0,99; 0,19; 0,88; 0,59; 0,78

2. Frekvenca prejema prijav za storitev je podvržena eksponentnemu zakonu porazdelitve () , x, parameter l je znan (v nadaljevanju l = 1/t - intenzivnost prejema prijav)

l=0,5 zahtev/uro. Določite zaporedje vrednosti za trajanje intervalov med prejemi zahtevkov. Število realizacij je enako 5. Število r j: 0,10; 0,12; 0,37; 0,09; 0,65; 0,99;

AKTIVNOST 2

Sistem čakalne vrste

Sistemi, v katerih na eni strani obstajajo množične zahteve za izvajanje katere koli vrste storitev, na drugi strani pa so te zahteve izpolnjene, se imenujejo čakalne vrste. Vsak QS služi za izpolnitev toka zahtev.

QS vključuje: vir zahtev, dohodni tok, čakalno vrsto, servisno napravo, odhodni tok zahtev.

SMO se delijo na:

QS z izgubami (napakami)

CMO s čakanjem (neomejena čakalna vrsta)

QS z omejeno dolžino čakalne vrste

CMO z omejeno čakalno dobo.

Glede na število kanalov oziroma servisnih naprav so QS enokanalni in večkanalni.

Glede na lokacijo vira zahtev: odprta in zaprta.

Po številu servisnih elementov na zahtevo: enofazni in večfazni.

Ena od oblik klasifikacije je klasifikacija D. Kendall - A / B / X / Y / Z

A - določa razporeditev časa med prihodi;

B - določa porazdelitev delovnega časa;

X - določa število servisnih kanalov;

Y - določa prepustnost sistema (dolžina čakalne vrste);

Z - določa vrstni red storitve.

Ko je zmogljivost sistema neskončna in je vrstni red storitve prvi prispe, prvi melje, so deli Y/Z izpuščeni. Prva številka (A) uporablja naslednje znake:

M-porazdelitev ima eksponentni zakon,

G - odsotnost kakršnih koli predpostavk o servisnem procesu ali pa je označen s simbolom GI, kar pomeni ponavljajoč se servisni proces,

D- determinističen (čas storitve je fiksen),

Е n - Erlangian n-tega reda,

NM n - hiper-erlangian n-tega reda.

Druga številka (B) uporablja iste znake.

Četrta številka (Y) prikazuje kapaciteto medpomnilnika, tj. največje število sedežev v čakalni vrsti.

Peta številka (Z) označuje način izbire iz čakalne vrste v čakalnem sistemu: SP-equiprobable, FF-first in-first out, LF-last in-first out, PR-priority.

Za naloge:

l - povprečno število vlog, ki prispejo na časovno enoto

µ je povprečno število opravljenih zahtevkov na časovno enoto

Faktor obremenitve kanala 1 ali odstotek časa, ko je kanal zaseden.

Glavne značilnosti:

1) P ref - verjetnost okvare - verjetnost, da bo sistem zavrnil storitev in bo zahteva izgubljena. To se zgodi, ko je kanal ali vsi kanali zasedeni (PSTN).

Za večkanalni QS R otk = R n, kjer je n število servisnih kanalov.

Za QS z omejeno dolžino čakalne vrste Р otk =Р n + l , kjer je l dovoljena dolžina čakalne vrste.

2) Relativni q in absolutni A prepustnost sistema

q \u003d 1-P otk A \u003d ql

3) Skupno število zahtev v sistemu

L sys = n - za QS z neuspehi, n je število kanalov, ki jih zaseda storitev.

Za QS s čakanjem in omejeno čakalno vrsto

L sistem \u003d n + L kul

kjer je L exp povprečno število zahtev, ki čakajo na začetek storitve itd.

Preostale značilnosti bomo upoštevali med reševanjem problemov.

Enokanalni in večkanalni čakalni sistemi. Sistemi okvar.

Najenostavnejši enokanalni model z verjetnostnim vhodnim tokom in servisno proceduro je model, za katerega je značilna eksponentna porazdelitev tako trajanja intervalov med prispelimi reklamacijami kot trajanja servisiranja. V tem primeru ima porazdelitvena gostota trajanja intervalov med prispelimi zahtevki obliko

Gostota porazdelitve trajanja storitve:

Tokovi zahtevkov in storitev so najenostavnejši. Naj sistem deluje z napakami. Ta tip QS se lahko uporablja pri modeliranju prenosnih kanalov v lokalnih omrežjih. Določiti je treba absolutno in relativno prepustnost sistema. Predstavimo ta čakalni sistem kot graf (slika 2), ki ima dve stanji:

S 0 - kanal je prost (čaka);

S 1 - kanal je zaseden (zahteva se servisira).

Slika 2. Graf stanj enokanalne QS z okvarami

Označimo verjetnosti stanj: P 0 (t) - verjetnost stanja "kanal je prost"; P 1 (t) - verjetnost stanja "kanal je zaseden". Na podlagi označenega grafa stanj sestavimo sistem Kolmogorovih diferencialnih enačb za verjetnosti stanj:

Sistem linearnih diferencialnih enačb ima rešitev pod pogojem normalizacije P 0 (t) + P 1 (t) = 1 . Rešitev tega sistema se imenuje nestacionarna, saj je neposredno odvisna od t in izgleda takole:

P 1 (t) = 1 - P 0 (t) (3.4.3)

Preprosto je videti, da za enokanalni QS z napakami verjetnost P 0 (t) ni nič drugega kot relativna zmogljivost sistema q. Dejansko je P 0 verjetnost, da je kanal ob času t prost in bo zahtevek, ki je prispel ob času t, servisiran, zato je za dani čas t povprečno razmerje med številom servisiranih zahtevkov in številom vhodnih terjatev je prav tako enaka P 0 (t), tj. q = P 0 (t).

Po dolgem časovnem intervalu (at) je dosežen stacionarni način (steady-state):

Če poznamo relativno prepustnost, je enostavno najti absolutno. Absolutna prepustnost (A) - povprečno število aplikacij, ki jih sistem čakalne vrste lahko oskrbi na časovno enoto:

Verjetnost zavrnitve storitve zahteve bo enaka verjetnosti stanja "kanal je zaseden":

To vrednost P otk je mogoče interpretirati kot povprečni delež neoskrbljenih zahtevkov med predloženimi.

V veliki večini primerov so sistemi čakalnih vrst v praksi večkanalni, zato so modeli z n servirnimi kanali (kjer n>1) nedvomno zanimivi. Za proces čakalne vrste, ki ga opisuje ta model, je značilna intenzivnost vhodnega toka l, medtem ko vzporedno ni mogoče oskrbeti več kot n strank (zahtev). Povprečni čas storitve za eno zahtevo je 1/min. Vhodni in izhodni tok sta Poissonova. Način delovanja enega ali drugega servisnega kanala ne vpliva na način delovanja drugih servisnih kanalov sistema, trajanje storitvenega postopka za vsakega od kanalov pa je naključna spremenljivka, za katero velja eksponentni zakon porazdelitve. Končni cilj uporabe n vzporedno povezanih servisnih kanalov je povečati (v primerjavi z enokanalnim sistemom) hitrost servisiranja zahtevkov s hkratno oskrbo n strank. Graf stanja večkanalnega čakalnega sistema z napakami ima obliko, prikazano na sliki 4.

Slika 4. Graf stanj večkanalne QS z okvarami

S 0 - vsi kanali so brezplačni;

S 1 - en kanal je zaseden, ostali so prosti;

S k - natanko k kanalov je zasedenih, ostali so prosti;

S n - vseh n kanalov je zasedenih, ostali so prosti.

Kolmogorove enačbe za verjetnosti stanj sistema P 0 , ... ,P k , ... P n bodo imele naslednjo obliko:

Začetni pogoji za rešitev sistema so naslednji:

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0 .

Stacionarna rešitev sistema ima obliko:

Formule za izračun verjetnosti P k (3.5.1) imenujemo Erlangove formule.

Določimo verjetnostne značilnosti delovanja večkanalnega QS z napakami v stacionarnem načinu:

1) verjetnost okvare:

saj je zahteva zavrnjena, če prispe v trenutku, ko je vseh n kanalov zasedenih. Vrednost P otk označuje popolnost storitve dohodnega toka;

2) verjetnost, da bo aplikacija sprejeta v storitev (je tudi relativna prepustnost sistema q), dopolnjuje P otk na enoto:

3) absolutna pasovna širina

4) povprečno število kanalov, ki jih zaseda storitev (), je naslednje:

Vrednost označuje stopnjo obremenitve QS.

Nalogena lekcijo 2

1. Komunikacijska veja, ki ima en kanal, sprejema najenostavnejši tok sporočil z intenzivnostjo n = 0,08 sporočil na sekundo. Čas prenosa je porazdeljen po zakonu exp. Servisiranje enega sporočila poteka z intenzivnostjo µ=0,1. Sporočila, ki prispejo v času, ko je strežni kanal zaseden s prenosom predhodno prejetega sporočila, prejmejo napako pri prenosu.

Coeff. Relativna obremenitev kanala (verjetnost, da je kanal zaseden)

p

Q je relativna zmogljivost internodalne veje

In absolutna pasovna širina komunikacijske veje.

2. Komunikacijska veja ima en kanal in sprejema sporočila vsakih 10 sekund. Čas storitve za eno sporočilo je 5 sekund. Čas prenosa sporočila je porazdeljen eksponentno. Sporočila, ki prispejo v času, ko je kanal zaseden, so zavrnjena.

Določite

Р zan - verjetnost zasedenosti komunikacijskega kanala (faktor relativne obremenitve)

Q- relativna pasovna širina

A je absolutna pasovna širina komunikacijske veje

4. Internodalna veja sekundarnega komunikacijskega omrežja ima n = 4 kanale. Pretok sporočil, ki prihajajo za prenos po kanalih komunikacijske veje, ima hitrost = 8 sporočil na sekundo. Povprečni čas prenosa enega sporočila je t = 0,1 sekunde Sporočilo, ki prispe v trenutku, ko je zasedenih vseh n kanalov, prejme napako pri prenosu po komunikacijski veji. Poiščite značilnosti CMO:

AKTIVNOST 3

Enokanalni sistem s čakanjem

Razmislite zdaj o enokanalnem QS s pričakovanjem. Sistem čakalne vrste ima en kanal. Vhodni tok zahtevkov za storitve je najenostavnejši tok z intenzivnostjo. Intenzivnost storitvenega toka je enaka (tj. v povprečju bo stalno zaseden kanal izdal servisirane zahteve). Trajanje storitve je naključna spremenljivka, za katero velja eksponentni porazdelitveni zakon. Storitveni tok je najenostavnejši Poissonov tok dogodkov. Zahteva, ki prispe v času, ko je kanal zaseden, je v čakalni vrsti in čaka na storitev. Ta QS je najpogostejši v modeliranju. Z eno ali drugo stopnjo približevanja se lahko uporablja za simulacijo skoraj katerega koli vozlišča lokalnega omrežja (LAN).

Recimo, da ne glede na to, koliko zahtevkov vstopi v vhod strežnega sistema, ta sistem (čakalna vrsta + streženi odjemalci) ne morem prilagoditi več kot N-zahtev (vlog), kar pomeni, da so stranke, ki ne padejo v čakalno dobo, prisiljene biti postrežene drugje. Sistem M/M/1/N. Nazadnje ima vir, ki generira storitvene zahteve, neomejeno (neskončno veliko) zmogljivost. Graf stanja QS ima v tem primeru obliko, prikazano na sliki 3

Slika 3. Graf stanj enokanalnega QS s čakanjem (shema smrti in razmnoževanja)

Stanja QS imajo naslednjo razlago:

S 0 - "kanal je brezplačen";

S 1 - "kanal je zaseden" (ni čakalne vrste);

S 2 - "kanal je zaseden" (ena aplikacija je v čakalni vrsti);

S n - "kanal je zaseden" (n -1 aplikacij je v čakalni vrsti);

S N - "kanal je zaseden" (N - 1 aplikacija je v čakalni vrsti).

Stacionarni proces v tem sistemu bo opisan z naslednjim sistemom algebraičnih enačb:

kjer je p = faktor obremenitve

n - državna številka.

Rešitev zgornjega sistema enačb za naš model QS ima obliko:

Začetna vrednost verjetnosti za QS z omejeno dolžino čakalne vrste

Za QS z neskončno čakalno vrsto H =? :

P 0 \u003d 1- s (3.4.7)

Opozoriti je treba, da izpolnjevanje pogoja stacionarnosti za ta QS ni potrebno, saj se število prijav, sprejetih v strežni sistem, nadzoruje z uvedbo omejitve dolžine čakalne vrste, ki ne sme preseči (N - 1), in ne z razmerjem med jakostmi vhodnega toka, torej ne z razmerjem c=l/m.

V nasprotju z enokanalnim sistemom, ki je bil obravnavan zgoraj in z neomejeno čakalno vrsto, v tem primeru obstaja stacionarna porazdelitev števila zahtev za vse končne vrednosti faktorja obremenitve c.

Določimo značilnosti enokanalnega QS s čakanjem in omejeno dolžino čakalne vrste, ki je enaka (N - 1) (M/M/1/N), kot tudi za enokanalni QS z neomejeno kapaciteto medpomnilnika ( M/M/1/?). Za QS z neskončno čakalno vrsto velja pogoj z<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) verjetnost zavrnitve storitve aplikacije:

Ena najpomembnejših značilnosti sistemov, v katerih se zahteve lahko izgubijo, je verjetnost izgube P, da bo poljubna zahteva izgubljena. V tem primeru verjetnost izgube poljubne zahteve sovpada z verjetnostjo, da so v poljubnem trenutku zasedena vsa čakalna mesta, tj. velja formula P iz k \u003d P H

2) relativna prepustnost sistema:

Za CMO z neomejenimčakalna vrsta q=1, Ker vse prijave bodo postrežene

3) absolutna pasovna širina:

4) povprečno število aplikacij v sistemu:

L S z neomejeno čakalno vrsto

5) povprečni čas zadrževanja aplikacije v sistemu:

Za neomejeno čakalno vrsto

6) povprečno trajanje čakanja stranke (prijave) v čakalni vrsti:

Z neomejeno čakalno vrsto

7) povprečno število prijav (strank) v čakalni vrsti (dolžina čakalne vrste):

z neomejeno čakalno vrsto

Če primerjamo izraze za povprečni čakalni čas v čakalni vrsti T pt in formulo za povprečno dolžino čakalne vrste L pt ter povprečni čas zadrževanja zahtevkov v sistemu T S in povprečno število zahtevkov v sistemu L S , vidimo to

L och \u003d l * T och L s \u003d l * T s

Upoštevajte, da so te formule veljavne tudi za številne sisteme čakalne vrste, ki so bolj splošni od obravnavanega sistema M/M/1 in se imenujejo Littlejeve formule. Praktični pomen teh formul je v tem, da odpravljajo potrebo po neposrednem izračunu vrednosti T och in T s z znano vrednostjo vrednosti L och in L s in obratno.

Naloge za enokanalne CMOs pričakovanjem, zpričakovanje inomejena dolžina čakalne vrste

1. Podan enovrstični QS z neomejenim akumulatorjem čakalne vrste. Prijave prispejo vsakih t =14 sekund. Povprečni čas prenosa enega sporočila je t=10 sekund. Sporočila, ki prispejo v času, ko je strežni kanal zaseden, so sprejeta v čakalno vrsto, ne da bi jo zapustili, dokler se storitev ne začne.

Določite naslednje kazalnike uspešnosti:

2. Internodalna veja komunikacije, ki ima en kanal in pogon čakalne vrste za m=3 čakajočih sporočil (N-1=m), sprejme najenostavnejši tok sporočil s hitrostjo n=5 sporočil. v sek.. Čas prenosa sporočila je porazdeljen po eksponentnem zakonu. Povprečni čas prenosa enega sporočila je 0,1 sekunde. Sporočila, ki prispejo v času, ko je strežni kanal zaseden s prenosom predhodno prejetega sporočila in na pogonu ni prostega prostora, se zavrnejo.

Р otk - verjetnost neuspešnega prejema sporočila

L syst - povprečno skupno število sporočil v čakalni vrsti in prenesenih po komunikacijski veji

T och - povprečni čas, ko sporočilo ostane v čakalni vrsti pred začetkom prenosa

T syst - povprečni skupni čas, ki ga sporočilo porabi v sistemu, vsota povprečnega časa čakanja v čakalni vrsti in povprečnega časa prenosa

Q- relativna pasovna širina

A je absolutna prepustnost

3. Internodalna veja sekundarnega komunikacijskega omrežja, ki ima en kanal in skladišče čakalne vrste za m = 4 (N-1=4) čakajočih sporočil, sprejema najenostavnejši tok sporočil s hitrostjo = 8 sporočil na sekundo. Čas prenosa sporočila je porazdeljen eksponentno. Povprečni čas prenosa enega sporočila je t = 0,1 sekunde. Sporočila, ki prispejo v času, ko je strežni kanal zaseden s prenosom predhodno prejetega sporočila in na pogonu ni prostega prostora, so v čakalni vrsti zavrnjena.

P otk - verjetnost neuspešnega sprejema sporočila za prenos po komunikacijskem kanalu internodalne veje;

L och - povprečno število sporočil v čakalni vrsti do komunikacijske veje sekundarnega omrežja čakalne vrste;

L syst - povprečno skupno število sporočil v čakalni vrsti in prenesenih prek komunikacijske veje sekundarnega omrežja;

T och - povprečni čas, ko sporočilo ostane v čakalni vrsti pred začetkom prenosa;

Р zan - verjetnost zasedenosti komunikacijskega kanala (koeficient relativne obremenitve kanala);

Q je relativna zmogljivost internodalne veje;

A je absolutna zmogljivost internodalne veje;

4. Internodalna komunikacijska veja, ki ima en kanal in pogon čakalne vrste za m=2 čakajočih sporočil, sprejme najenostavnejši tok sporočil z intenzivnostjo n=4 sporočil. v sek.. Čas prenosa sporočila je porazdeljen po eksponentnem zakonu. Povprečni čas prenosa enega sporočila je 0,1 sekunde. Sporočila, ki prispejo v času, ko je strežni kanal zaseden s prenosom predhodno prejetega sporočila in na pogonu ni prostega prostora, se zavrnejo.

Določite naslednje kazalnike uspešnosti komunikacijske veje:

Р otk - verjetnost neuspešnega prejema sporočila

L och - povprečno število sporočil v čakalni vrsti do komunikacijske veje

L syst - povprečno skupno število sporočil v čakalni vrsti in prenesenih po komunikacijski veji

T och - povprečni čas, ko sporočilo ostane v čakalni vrsti pred začetkom prenosa

T syst - povprečni skupni čas, ki ga sporočilo porabi v sistemu, vsota povprečnega časa čakanja v čakalni vrsti in povprečnega časa prenosa

Р zan - verjetnost zasedenosti komunikacijskega kanala (koeficient relativne obremenitve kanala c)

Q- relativna pasovna širina

A je absolutna prepustnost

5. Internodalna veja sekundarnega komunikacijskega omrežja, ki ima en kanal in neomejeno čakalno vrsto za shranjevanje čakajočih sporočil, sprejema najenostavnejši tok sporočil z intenzivnostjo n = 0,06 sporočil na sekundo. Povprečni čas prenosa enega sporočila t =10 sekund. Sporočila, ki prispejo v času, ko je komunikacijski kanal zaseden, se sprejmejo v čakalno vrsto in je ne zapustijo do začetka storitve.

Določite naslednje kazalnike uspešnosti komunikacijske veje sekundarnega omrežja:

L och - povprečno število sporočil v čakalni vrsti do komunikacijske veje;

L syst - povprečno skupno število sporočil v čakalni vrsti in prenesenih po komunikacijski veji;

T och - povprečni čas, ki ga sporočilo porabi v čakalni vrsti;

T syst je povprečni skupni čas, ki ga sporočilo preživi v sistemu, ki je vsota povprečnega časa čakanja v čakalni vrsti in povprečnega časa prenosa;

Р zan - verjetnost zasedenosti komunikacijskega kanala (koeficient relativne obremenitve kanala);

Q je relativna zmogljivost internodalne veje;

A - absolutna prepustnost internodalne veje

6. Podan enovrstični QS z neomejenim akumulatorjem čakalne vrste. Prijave prispejo vsakih t =13 sekund. Povprečni čas prenosa na sporočilo

t=10 sekund. Sporočila, ki prispejo v času, ko je strežni kanal zaseden, so sprejeta v čakalno vrsto, ne da bi jo zapustili, dokler se storitev ne začne.

Določite naslednje kazalnike uspešnosti:

L och - povprečno število sporočil v čakalni vrsti

L syst - povprečno skupno število sporočil v čakalni vrsti in prenesenih po komunikacijski veji

T och - povprečni čas, ko sporočilo ostane v čakalni vrsti pred začetkom prenosa

T syst - povprečni skupni čas, ki ga sporočilo porabi v sistemu, vsota povprečnega časa čakanja v čakalni vrsti in povprečnega časa prenosa

Р zan - verjetnost zasedenosti (koeficient relativne obremenitve kanala c)

Q- relativna pasovna širina

A je absolutna prepustnost

7. Specializirano diagnostično mesto je enokanalni QS. Število parkirnih mest za avtomobile, ki čakajo na diagnostiko, je omejeno in znaša 3 [(N - 1) = 3]. Če so vsa parkirišča zasedena, torej so že trije avtomobili v čakalni vrsti, potem naslednji avto, ki je prišel na diagnostiko, ne pride v servisno čakalno vrsto. Tok avtomobilov, ki prihajajo na diagnostiko, je porazdeljen po Poissonovem zakonu in ima intenziteto = 0,85 (avtomobilov na uro). Čas diagnostike avtomobila je razporejen po eksponentnem zakonu in v povprečju znaša 1,05 ure.

Potrebno je določiti verjetnostne značilnosti diagnostičnega mesta, ki deluje v stacionarnem načinu: P 0, P 1, P 2, P 3, P 4, P odprto, q, A, L och, L sys, T och, T sis

AKTIVNOST 4

Večkanalni QS s čakanjem, s čakanjem in omejeno čakalno vrsto

Razmislite o večkanalnem čakalnem sistemu s čakanjem. Ta tip QS se pogosto uporablja pri modeliranju skupin naročniških terminalov LAN, ki delujejo v on-line načinu. Za proces čakalne vrste je značilno naslednje: vhodni in izhodni tokovi so Poissonovi z intenzivnostjo oz. vzporedno ni mogoče oskrbovati več kot n strank. Sistem ima n servisnih kanalov. Povprečni čas storitve na stranko je 1/m za vsak kanal. Ta sistem se nanaša tudi na proces smrti in razmnoževanja.

с=l/nm - razmerje med intenzivnostjo dovodnega toka in skupno intenzivnostjo storitve, je faktor obremenitve sistema

(Z<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

kjer je Р 0 verjetnost prostega stanja vseh kanalov z neomejeno čakalno vrsto, k je število aplikacij.

če sprejmemo c=l / m, potem lahko P 0 določimo za neomejeno čakalno vrsto:

Za omejeno čakalno vrsto:

kjer je m dolžina čakalne vrste

Z neomejeno čakalno vrsto:

Relativna prepustnost q=1,

Absolutna pasovna širina A \u003d l,

Povprečno število zasedenih kanalov Z=A/m

Z omejeno čakalno vrsto

1 Internodalna veja sekundarnega komunikacijskega omrežja ima n = 4 kanale. Pretok sporočil, ki prihajajo za prenos po kanalih komunikacijske veje, ima hitrost = 8 sporočil na sekundo. Povprečni čas t = 0,1 za prenos enega sporočila po vsakem komunikacijskem kanalu je t/n = 0,025 sekunde. Čakalna doba za sporočila v čakalni vrsti je neomejena. Poiščite značilnosti CMO:

R otk - verjetnost neuspešnega prenosa sporočil;

Q je relativna prepustnost komunikacijske veje;

A je absolutna pasovna širina komunikacijske veje;

Z je povprečno število zasedenih kanalov;

L och - povprečno število sporočil v čakalni vrsti;

T exp - povprečni čakalni čas;

T syst - povprečni skupni čas, ki ga sporočila porabijo v čakalni vrsti in prenos po komunikacijski veji.

2. Mehanska delavnica obrata s tremi delovnimi mesti (kanali) opravlja popravila male mehanizacije. Tok okvarjenih mehanizmov, ki prihajajo v delavnico, je poissonov in ima intenziteto = 2,5 mehanizmov na dan, povprečni čas popravila enega mehanizma pa je porazdeljen po eksponentnem zakonu in je enak = 0,5 dni. Predpostavimo, da v tovarni ni druge delavnice, zato lahko vrsta mehanizmov pred delavnico raste skoraj za nedoločen čas. Potrebno je izračunati naslednje mejne vrednosti verjetnostnih značilnosti sistema:

Verjetnosti sistemskih stanj;

Povprečno število aplikacij v servisni čakalni vrsti;

Povprečno število aplikacij v sistemu;

Povprečno trajanje prijave v čakalni vrsti;

Povprečno trajanje bivanja aplikacije v sistemu.

3. Internodalna veja sekundarnega komunikacijskega omrežja ima n=3 kanale. Tok sporočil, ki prihajajo v prenos po kanalih komunikacijske veje, ima intenziteto n=5 sporočil na sekundo. Povprečni čas prenosa enega sporočila je t=0,1, t/n=0,033 sek.. V pogon čakalne vrste sporočil je mogoče shraniti do m= 2 sporočila. Sporočilo, ki prispe v času, ko so vsa mesta v čakalni vrsti zasedena, prejme zavrnitev prenosa na komunikacijski veji. Poiščite značilnosti QS: P otk - verjetnost neuspešnega prenosa sporočila, Q - relativna prepustnost, A - absolutna prepustnost, Z - povprečno število zasedenih kanalov, L och - povprečno število sporočil v čakalni vrsti, T exp - povprečno čakanje. čas, sistem T - povprečni skupni čas, ki ga sporočilo porabi v čakalni vrsti in njegov prenos po komunikacijski veji.

AKTIVNOST 5

Zaprt QS

Oglejmo si model servisiranja strojnega parka, ki je model zaprtega čakalnega sistema. Do sedaj smo obravnavali le takšne sisteme čakalnih vrst, pri katerih intenzivnost vhodnega toka zahtevkov ni odvisna od stanja sistema. V tem primeru je vir zahtevkov zunaj QS in ustvarja neomejen tok zahtevkov. Razmislite o sistemih čakalnih vrst, za katere je odvisno od stanja sistema, kjer je vir zahtev notranji in ustvarja omejen pretok zahtev. Na primer, strojni park, sestavljen iz N strojev, servisira ekipa R mehanikov (N > R), vsak stroj pa lahko servisira samo en mehanik. Tu so stroji viri zahtev (zahtev za servis), mehaniki pa servisni kanali. Okvarjen stroj po servisu se uporabi za predvideni namen in postane potencialni vir servisnih potreb. Očitno je intenzivnost odvisna od tega, koliko avtomobilov trenutno obratuje (N - k) in koliko avtomobilov je na servisu ali čaka na servis (k). V obravnavanem modelu je treba zmogljivost vira zahtev šteti za omejeno. Vhodni tok zahtev prihaja iz omejenega števila delujočih strojev (N - k), ki ob naključnih trenutkih odpovejo in zahtevajo vzdrževanje. Poleg tega deluje vsak stroj iz (N - k). Generira Poissonov tok povpraševanja z intenzivnostjo X ne glede na druge objekte, skupni vhodni tok ima intenzivnost. Zahteva, ki pride v sistem v trenutku, ko je vsaj en kanal prost, se takoj pošlje v servis. Če zahteva ugotovi, da so vsi kanali zasedeni z drugimi zahtevami, potem ne zapusti sistema, ampak se postavi v čakalno vrsto in počaka, da se eden od kanalov sprosti. Tako se v zaprtem sistemu čakalne vrste dohodni tok zahtev oblikuje iz odhodnega. Za stanje S k sistema je značilno skupno število zahtev, ki so servisirane in v čakalni vrsti, enako k. Za obravnavani zaprti sistem je očitno k = 0, 1, 2, ..., N. Še več, če je sistem v stanju S k, potem je število objektov v delovanju (N - k). Če - intenzivnost pretoka zahtev na stroj, potem:

Sistem algebraičnih enačb, ki opisuje delovanje zaprtega QS v stacionarnem načinu, je naslednji:

Če rešimo ta sistem, najdemo verjetnost k-tega stanja:

Vrednost P 0 je določena iz pogoja normalizacije rezultatov, dobljenih s formulami za P k , k = 0, 1, 2, ..., N. Določimo naslednje verjetnostne značilnosti sistema:

Povprečno število zahtevkov v servisni čakalni vrsti:

Povprečno število zahtevkov v sistemu (v servisu in v čakalni vrsti)

povprečno število mehanikov (kanalov) "v mirovanju" zaradi pomanjkanja dela

Razmerje izpadov servisiranega objekta (stroja) v čakalni vrsti

Stopnja izkoriščenosti objektov (strojev)

Razmerje izpadov servisnih kanalov (mehanika)

Povprečna čakalna doba na storitev (čas čakanja na storitev v čakalni vrsti)

Zaprta težava QS

1. Naj bosta dva inženirja enake produktivnosti dodeljena za servisiranje desetih osebnih računalnikov (PC). Tok okvar (napak) enega računalnika je Poisson z intenziteto = 0,2. Čas delovanja osebnega računalnika se ravna po eksponentnem zakonu. Povprečni čas vzdrževanja enega osebnega računalnika s strani enega inženirja je: = 1,25 ure. Na voljo so naslednje možnosti organizacije storitev:

Oba inženirja služita vsem desetim računalnikom, tako da če PC odpove, ga streže eden od prostih inženirjev, v tem primeru R = 2, N = 10;

Vsak od obeh inženirjev vzdržuje pet računalnikov, ki so mu dodeljeni. V tem primeru je R = 1, N = 5.

Treba je izbrati najboljšo možnost za organizacijo vzdrževanja računalnika.

Treba je definirati vse verjetnosti stanj P k: P 1 - P 10, glede na to in z uporabo rezultatov izračuna P k izračunamo P 0

AKTIVNOST 6

Izračun prometa.

Teorija teleprometa je del teorije čakalne vrste. Temelje teorije teleprometa je postavil danski znanstvenik A.K. Erlang. Njegova dela so bila objavljena v letih 1909-1928. Naj navedemo pomembne definicije, ki se uporabljajo v teoriji teleprometa (TT). Izraz "traffic" (angleško, traffic) ustreza izrazu "telephone load". Pomeni obremenitev, ki jo ustvari pretok klicev, zahtev, sporočil, ki prihajajo na vhode QS. Obseg prometa se imenuje vrednost celotnega, integralnega časovnega intervala, ki ga je zamudil en ali drug vir, med katerim je bil ta vir zaseden v analiziranem časovnem obdobju. Enota dela se lahko šteje za drugo zasedbo vira. Včasih lahko berete približno ure, včasih pa le sekunde ali ure. Vendar pa priporočila ITU podajajo razsežnost obsega prometa v erlango urah. Za razumevanje pomena takšne merske enote je treba upoštevati še en prometni parameter - intenzivnost prometa. V tem primeru pogosto govorijo o povprečni intenzivnosti prometa (obremenitvi) na danem bazenu (naboru) virov. Če je v vsakem trenutku t iz danega intervala (t 1 ,t 2) število virov iz tega niza, ki jih zaseda servisiranje prometa, enako A(t), potem bo povprečna intenzivnost prometa

Vrednost intenzivnosti prometa je označena kot povprečno število virov, ki jih promet zaseda v določenem časovnem intervalu. Merska enota intenzivnosti obremenitve je en Erlang (1 Erl, 1 E), t.j. 1 erlang je intenzivnost prometa, ki zahteva polno zaposlenost enega vira ali z drugimi besedami, pri kateri delo ene sekunde opravi vir - zasedenost za čas ene sekunde. V ameriški literaturi lahko včasih najdete še eno mersko enoto, imenovano CCS-Centrum (ali sto) Calls Second (hektosekunda poklicev). Številka CCS odraža čas, ko so strežniki zasedeni v 100-sekundnih intervalih v eni uri. Intenzivnost, izmerjeno v CCS, je mogoče pretvoriti v Erlange z uporabo formule 36CCS=1 Erl.

Promet, ki ga ustvari en vir in je izražen v urah-sejah, je enak zmnožku števila poskusov klicev c za določen časovni interval T in povprečnega trajanja enega poskusa t: y = c t (h-h). Promet je mogoče izračunati na tri različne načine:

1) naj bo število klicev c na uro 1800 in povprečno trajanje lekcije t = 3 minute, potem je Y = 1800 klicev. /h 0,05 h = 90 Erl;

2) naj bodo trajanja t i vseh n zasedenosti izhodov določenega snopa fiksirana v času T, potem je promet določen na naslednji način:

3) naj v času T poteka opazovanje v enakomernih intervalih nad številom sočasno zasedenih izhodov določenega žarka, glede na rezultate opazovanj se zgradi stopenjska funkcija časa x(t) (slika 8) .

Slika 8. Število sočasno zasedenih izhodov snopa

Promet v času T je mogoče oceniti kot povprečno vrednost x(t) v tem času:

kjer je n število vzorcev sočasno zasedenih izhodov. Vrednost Y je povprečno število istočasno zasedenih izhodov snopa v času T.

Nihanja v prometu. Promet sekundarnih telefonskih omrežij skozi čas močno niha. Med delovnikom ima prometna krivulja dva ali celo tri vrhove (Slika 9).

Slika 9. Nihanje prometa čez dan

Ura dneva, v kateri je dolgoročni promet največji, se imenuje ura zasedenosti (BUSH). Poznavanje prometa v CNN je temeljnega pomena, saj določa število kanalov (linij), količino opreme postaj in vozlišč. Promet na isti dan v tednu ima sezonska nihanja. Če je dan v tednu dan pred praznikom, potem je NPV tega dne višja kot dan po prazniku. Če raste število storitev, ki jih podpira omrežje, raste tudi promet. Zato je problematično z zadostno gotovostjo napovedati pojav prometnih konic. Promet skrbno spremljajo uprava omrežja in projektantske organizacije. Pravila za merjenje prometa razvija ITU-T in jih uporabljajo nacionalne omrežne uprave za izpolnjevanje zahtev glede kakovosti storitev tako za naročnike lastnega omrežja kot za naročnike drugih omrežij, povezanih z njim. Teorijo teleprometa lahko uporabimo za praktične izračune izgub ali prostornine opreme postaje (vozlišča) samo, če promet miruje (statistično enakomeren). Ta pogoj je približno izpolnjen s prometom na CNN. Količina obremenitve, ki jo prejme PBX na dan, vpliva na preprečevanje in popravilo opreme. Neenakomernost obremenitve postaje čez dan je določena s koeficientom koncentracije

Bolj stroga definicija NNN je naslednja. Priporočilo ITU E.500 predpisuje analizo podatkov o intenzivnosti za 12 mesecev, med njimi izberite 30 najbolj obremenjenih dni, poiščite najbolj obremenjene ure v teh dneh in povprečje rezultatov meritev intenzivnosti v teh intervalih. Ta izračun intenzivnosti prometa (obremenitev) se imenuje običajna ocena intenzivnosti prometa v obremenjeni uri ali ravni A. Strožja ocena je lahko povprečna za 5 najbolj obremenjenih dni v izbranem 30-dnevnem obdobju. Takšno oceno imenujemo povišana ali ocena stopnje B.

Postopek ustvarjanja prometa. Kot ve vsak uporabnik telefonskega omrežja, se vsi poskusi vzpostavitve povezave s klicanim naročnikom ne končajo uspešno. Včasih morate narediti več neuspešnih poskusov, preden se vzpostavi želena povezava.

Slika 10. Diagram dogodkov ob vzpostavitvi povezave med naročniki

Razmislimo o možnih dogodkih pri simulaciji vzpostavitve povezave med naročnikoma A in B (slika 10). Statistični podatki o klicih v telefonskih omrežjih so naslednji: delež opravljenih klicev je 70-50 %, delež neuspelih klicev je 30-50 %. Vsak poskus naročnika zasede vhod v QS. Pri uspešnih poskusih (ko je bil pogovor) je čas zasedenosti preklopnih naprav, ki vzpostavljajo povezave med vhodi in izhodi, daljši kot pri neuspešnih poskusih. Naročnik lahko kadarkoli prekine poskuse povezave. Ponovne poskuse lahko povzročijo naslednji razlogi:

Nepravilno izbrana številka;

Predpostavka o napaki v omrežju;

Stopnja nujnosti pogovora;

Neuspešni prejšnji poskusi;

Poznavanje navad naročnika B;

Dvom o pravilnem izbiranju.

Ponovni poskus bo morda možen glede na naslednje okoliščine:

Stopnje nujnosti;

Ocene vzrokov za neuspeh;

Ocene smotrnosti ponavljajočih se poskusov,

Ocene sprejemljivega intervala med poskusi.

Zavrnitev ponovnega poskusa je lahko povezana z nizko stopnjo nujnosti. Obstaja več vrst prometa, ki ga ustvarijo klici: dohodni (ponujeni) Y p in zgrešeni Y p. Promet Y p vključuje vse uspešne in neuspešne poskuse, promet Y p, ki je del Y p, vključuje uspešne in del neuspešnih poskusov:

Y pr \u003d Y p + Y np,

kjer je Y p - pogovorni (koristen) promet in Y np - promet, ustvarjen z neuspešnimi poskusi. Enakost Y p = Y p je mogoča le v idealnem primeru, če ni izgub, napak kličočih in odziva klicanih naročnikov.

Razlika med dohodnimi in zamujenimi obremenitvami v določenem časovnem obdobju bo izgubljena obremenitev.

Napovedovanje prometa. Omejeni viri povzročajo potrebo po postopnem širjenju postaje in omrežja. Administracija omrežja napoveduje povečanje prometa v razvojni fazi ob upoštevanju, da:

Dohodek določa delež pretečenega prometa Y p, - stroške določa kakovost storitve pri največjem prometu;

Velik delež izgub (nizka kakovost) se pojavi v redkih primerih in je značilen za konec razvojne dobe;

Največji obseg zamujenega prometa pade na obdobja, ko izgub praktično ni - če so izgube manjše od 10%, se naročniki nanje ne odzivajo. Pri načrtovanju razvoja postaj in omrežja mora projektant odgovoriti na vprašanje, kakšne so zahteve glede kakovosti izvajanja storitev (pri izgubah). Za to je treba izmeriti prometne izgube v skladu s pravili, sprejetimi v državi.

Primer merjenja prometa.

Najprej razmislite o tem, kako lahko prikažete delovanje QS, ki ima več virov, ki služijo določenemu prometu hkrati. Nadalje bomo govorili o virih, kot so strežniki, ki služijo toku aplikacij ali zahtev. Eden najbolj vizualnih in pogosto uporabljenih načinov za prikaz postopka servisiranja zahtev s strani skupine strežnikov je gantogram. Ta grafikon je pravokotni koordinatni sistem, katerega abscisa predstavlja čas, ordinata pa diskretne točke, ki ustrezajo strežnikom skupine. Slika 11 prikazuje gantogram za sistem s tremi strežniki.

V prvih treh časovnih intervalih (štejemo jih za sekundo) sta zasedena prvi in ​​tretji strežnik, naslednji dve sekundi - samo tretji, nato drugi deluje eno sekundo, nato drugi in prvi dve sekundi in zadnji dve sekundi - samo prva.

Konstruirani diagram vam omogoča izračun obsega prometa in njegove intenzivnosti. Diagram prikazuje le postrežen ali zgrešen promet, saj ne pove ničesar o tem, ali so v sistem vstopile zahteve, ki jih strežniki niso mogli postreči.

Obseg pretečenega prometa se izračuna kot skupna dolžina vseh segmentov gantograma. Glasnost v 10 sekundah:

Povežite z vsakim časovnim intervalom, narisanim na abscisi, celo število, ki je enako številu strežnikov, zasedenih v tem posameznem intervalu. Ta vrednost A(t) je trenutna jakost. Za naš primer

A(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Poiščimo zdaj povprečno intenzivnost prometa v obdobju 10 sekund

Tako je povprečna intenzivnost prometa, ki ga prepusti obravnavani sistem treh strežnikov, enaka 1,5 Erl.

Glavni parametri obremenitve

Telefonsko komunikacijo uporabljajo različne kategorije naročnikov, za katere so značilni:

število virov obremenitve - N,

povprečno število klicev iz enega vira v določenem času (običajno HNN) - s,

povprečno trajanje ene zasedbe preklopnega sistema pri servisiranju enega klica je t.

Intenzivnost obremenitve bo

Določimo različne vire klicev. na primer

Povprečno število klicev na službeni telefon na službeni telefon;

Povprečno število klicev iz ene stanovanjske posamezne naprave; naključni dogodek v čakalni vrsti teletraffic

s štetjem - enako iz aparata za skupno rabo;

z ma - enako iz enega avtomata za kovance;

s sl - enako iz ene povezovalne črte.

Potem je povprečno število klicev iz enega vira:

Obstajajo približni podatki za povprečno število klicev iz enega vira ustrezne kategorije:

3,5 - 5, \u003d 0,5 - 1, s štetjem \u003d 1,5 - 2, z ma \u003d 15 - 30, s sl \u003d 10 - 30.

Obstajajo naslednje vrste povezav, ki glede na izid povezave ustvarjajo različno telefonsko obremenitev postaje:

k p - koeficient, ki prikazuje delež povezav, ki so se končale s pogovorom;

k c - povezave, ki se niso zaključile s pogovorom zaradi zasedenosti klicanega naročnika;

k but - koeficient, ki izraža delež zvez, ki se niso zaključile s pogovorom zaradi neodziva klicanega naročnika;

k osh - povezave, ki se niso končale s pogovorom zaradi napak klicatelja;

k od teh - klici, ki se iz tehničnih razlogov niso končali s pogovorom.

Med normalnim delovanjem omrežja so vrednosti teh koeficientov enake:

k p =0,60-0,75; kc =0,12-0,15; k a =0,08-0,12; k osh =0,02-0,05; k tiste = 0,005-0,01.

Povprečno trajanje lekcije je odvisno od vrste povezav. Na primer, če se je povezava končala s pogovorom, bo povprečno trajanje zasedenosti naprav t stanje enako

kje je trajanje vzpostavitve povezave;

t kond. - pogovor, ki je potekal;

t in - trajanje pošiljanja klica na telefonski aparat klicanega naročnika;

t p - trajanje pogovora

kjer je t - signal odziva postaje;

1.5n - čas klicanja klicanega naročnika (n - število znakov v številki);

t s - čas, potreben za vzpostavitev povezave s preklopnimi mehanizmi in prekinitev povezave po koncu pogovora. Približne vrednosti obravnavanih količin:

t co \u003d 3 s, t c \u003d 1-2,5 s, t in \u003d 8-10 s, t p \u003d 90-130 s.

Obremenitev telefona povzročajo tudi klici, ki se ne končajo s pogovorom.

Povprečni čas zasedenosti naprav, ko je klicani naročnik zaseden, je enak

kjer je nastavljen t. določeno z (4.2.3)

t brenčalo - čas poslušanja zasedenega brenčala, t brenčalo =6sek.

Povprečno trajanje zasedenosti naprav, ko se klicani naročnik ne oglasi, je enako

kjer je t pv čas poslušanja krmilnega signala povratnega zvonjenja, t pv = 20 s.

Če pogovora ni bilo zaradi napak naročnika, potem je povprečno t osh = 30 sek.

Trajanje sej, ki se zaradi tehničnih razlogov niso končale s pogovorom, ni opredeljeno, saj je odstotek takih sej majhen.

Iz vsega navedenega izhaja, da je skupna obremenitev skupine virov za NTT enaka vsoti obremenitev posameznih vrst poklicev.

kjer je koeficient, ki upošteva pogoje kot deleže

Na telefonskem omrežju s sedemmestnim številčenjem je bila zasnovana avtomatska telefonska centrala, katere strukturna sestava naročnikov je naslednja:

N chr \u003d 4000, N ind \u003d 1000, N count \u003d 2000, N ma \u003d 400, N sl \u003d 400.

Povprečno število klicev iz enega vira v uri zasedenosti je

S formulama (4.2.3) in (4.2.6) najdemo obremenitev

1.10.62826767 s = 785.2 Hz.

Povprečno trajanje pouka t iz formule Y=Nct

t= Y/Nc= 2826767/7800*3,8=95,4 sek.

Naloži nalogo

1. Na telefonskem omrežju s sedemmestnim številčenjem je bila zasnovana avtomatska telefonska centrala, katere strukturna sestava naročnikov je naslednja:

N uchr \u003d 5000, N ind \u003d 1500, N count \u003d 3000, N ma = 500, N sl \u003d 500.

Določite tovor, ki prihaja na postajo - Y, povprečno trajanje zasedenosti t, če je znano, da

s chr \u003d 4, z ind \u003d 1, s štetjem \u003d 2, z ma \u003d 10, s sl \u003d 12, t p \u003d 120 s, t in \u003d 10 s, k p \u003d 0,6, t z \u003d 1 s., \u003d 1,1.

Gostuje na Allbest.ru

Podobni dokumenti

Koncept enakomerno porazdeljene naključne spremenljivke. Multiplikativna kongruentna metoda. Modeliranje zveznih naključnih spremenljivk in diskretnih porazdelitev. Algoritem za simulacijo ekonomskih odnosov med posojilodajalcem in posojilojemalcem.

seminarska naloga, dodana 1.3.2011


Splošni koncepti teorije čakalne vrste. Značilnosti modeliranja čakalnih sistemov. Grafi stanja QS, enačbe, ki jih opisujejo. Splošne značilnosti sort modelov. Analiza sistema čakalnih vrst v supermarketih.

seminarska naloga, dodana 17.11.2009


Elementi teorije čakalne vrste. Matematično modeliranje čakalnih sistemov, njihova klasifikacija. Simulacijsko modeliranje čakalnih sistemov. Praktična uporaba teorije, reševanje problemov z matematičnimi metodami.

seminarska naloga, dodana 04.05.2011


Koncept naključnega procesa. Naloge teorije čakalne vrste. Klasifikacija čakalnih sistemov (QS). Probabilistični matematični model. Vpliv naključnih dejavnikov na obnašanje objekta. Enokanalni in večkanalni QS s čakanjem.

seminarska naloga, dodana 25.09.2014


Študij teoretičnih vidikov učinkovite konstrukcije in delovanja sistema čakalnih vrst, njegovih glavnih elementov, klasifikacije, značilnosti in delovanja. Modeliranje sistema čakalne vrste v jeziku GPSS.

seminarska naloga, dodana 24.09.2010


Razvoj teorije dinamičnega programiranja, mrežnega načrtovanja in vodenja proizvodnje izdelkov. Komponente teorije iger v problemih modeliranja ekonomskih procesov. Elementi praktične uporabe teorije čakalnih vrst.

praktično delo, dodano 1.8.2011


Osnovni pojmi o naključnih dogodkih, količinah in funkcijah. Numerične značilnosti slučajnih spremenljivk. Vrste asimetrije porazdelitev. Statistično vrednotenje porazdelitve slučajnih spremenljivk. Reševanje problemov strukturno-parametrične identifikacije.

seminarska naloga, dodana 3.6.2012


Modeliranje procesa čakalne vrste. Različne vrste čakalnih kanalov. Rešitev enokanalnega modela čakalne vrste z napakami. Gostota porazdelitve trajanja storitve. Opredelitev absolutne prepustnosti.

test, dodan 15.3.2016


Funkcionalne značilnosti sistema čakalne vrste na področju cestnega prometa, njegova struktura in glavni elementi. Kvantitativni kazalniki kakovosti delovanja sistema čakalnih vrst, postopek in glavne faze njihovega določanja.

laboratorijske vaje, dodano 3. 11. 2011


Postavitev cilja modeliranja. Identifikacija realnih predmetov. Izbira vrste modelov, matematične sheme. Konstrukcija zvezno-stohastičnega modela. Osnovni koncepti teorije čakalnih vrst. Določite tok dogodkov. Izjava algoritmov.