Çevrimiçi işlevin aşırı noktaları. İki değişkenli bir fonksiyonun ekstremumu

Bu makaleden, okuyucu, aşırı fonksiyonel değerin ne olduğunu ve pratikte kullanımının özellikleri hakkında bilgi edinecektir. Böyle bir kavramın incelenmesi, yüksek matematiğin temellerini anlamak için son derece önemlidir. Bu konu, kursun daha derin bir çalışması için esastır.

Temas halinde

aşırı nedir?

Okul dersinde "aşırı" kavramının birçok tanımı verilmektedir. Bu makale, konuya ilgisiz olanlar için terimin en derin ve net anlayışını vermeyi amaçlamaktadır. Böylece terim, belirli bir kümede fonksiyonel aralığın ne ölçüde minimum veya maksimum değer elde ettiği anlaşılır.

Ekstremum, fonksiyonun aynı anda hem minimum hem de maksimum değeridir. Bir minimum nokta ve bir maksimum nokta vardır, yani grafikteki argümanın uç değerleri. Bu kavramın kullanıldığı ana bilimler:

• İstatistik;
• makine kontrolü;
• Ekonometri.

Uç noktalar, verilen bir fonksiyonun sırasını belirlemede önemli bir rol oynar. Grafikteki koordinat sistemi en iyi şekilde işlevsellikteki değişikliğe bağlı olarak uç konumdaki değişikliği gösterir.

Türev fonksiyonunun aşırılığı

Bir de "türev" diye bir şey var. Ekstremum noktasının belirlenmesi gereklidir. Minimum veya maksimum noktaları en büyük ve en küçük değerlerle karıştırmamak önemlidir. Bunlar benzer görünseler de farklı kavramlardır.

Fonksiyonun değeri, maksimum noktanın nasıl bulunacağını belirlemede ana faktördür. Türev, değerlerden değil, yalnızca bir sıradaki uç konumundan oluşur.

Türevin kendisi, en büyük veya en küçük değere değil, uç noktaların verilerine göre belirlenir. Rus okullarında, bu iki kavram arasındaki çizginin net olarak çizilmemesi, bu konunun genel olarak anlaşılmasını etkiler.

Şimdi böyle bir şeyi "keskin ekstremum" olarak ele alalım. Bugüne kadar, akut bir minimum değer ve akut bir maksimum değer vardır. Tanım, bir fonksiyonun kritik noktalarının Rus sınıflandırmasına göre verilmiştir. Bir ekstremum noktası kavramı, bir çizelgede kritik noktaları bulmanın temelidir.

Böyle bir kavramı tanımlamak için Fermat teoremi kullanılır. Uç noktaların incelenmesinde en önemlisidir ve varlıkları hakkında şu ya da bu şekilde net bir fikir verir. Aşırılığı sağlamak için, grafikte azalma veya artış için belirli koşullar oluşturmak önemlidir.

"Maksimum puan nasıl bulunur" sorusuna doğru bir şekilde cevap vermek için şu hükümleri izlemelisiniz:

1. Grafikte tam tanım alanını bulma.
2. Bir fonksiyonun türevini ve bir ekstremum noktası arayın.
3. Argümanın etki alanı için standart eşitsizlikleri çözün.
4. Grafikte bir noktanın hangi fonksiyonlarda tanımlı ve sürekli olduğunu ispatlayabilme.

Dikkat! Bir fonksiyonun kritik bir noktasının aranması, ancak, bir ekstremum noktasının yüksek oranda bulunmasıyla sağlanan en azından ikinci dereceden bir türev varsa mümkündür.

Fonksiyonun ekstremumu için gerekli koşul

Bir ekstremumun var olması için hem minimum noktaların hem de maksimum noktaların bulunması önemlidir. Bu kurala yalnızca kısmen uyulursa, bir ekstremumun varlığı koşulu ihlal edilir.

Herhangi bir konumdaki her işlev, yeni anlamlarını tanımlamak için farklılaştırılmalıdır. Bir noktanın ortadan kaybolmasının, türevlenebilir bir nokta bulmanın ana ilkesi olmadığını anlamak önemlidir.

Keskin bir ekstremum ve ayrıca bir fonksiyon minimumu, ekstrem değerler kullanarak bir matematik problemini çözmenin son derece önemli bir yönüdür. Bu bileşeni daha iyi anlamak için, işlevin atanması için tablo değerlerine başvurmak önemlidir.

Tam bir anlam keşfi

Bir Değer Çizmek

1. Değerlerin artış ve azalış noktalarının belirlenmesi. 2. Koordinat eksenleri ile kırılma noktaları, ekstremum ve kesişim bulma. 3. Haritadaki konum değişikliklerini belirleme süreci. 4. Asimptotların varlığını dikkate alarak dışbükeylik ve dışbükeylik indeksinin ve yönünün belirlenmesi. 5. Çalışmanın koordinatlarının belirlenmesi açısından özet tablosunun oluşturulması. 6. Aşırı ve akut noktaların artış ve azalma aralıklarını bulma. 7. Eğrinin dışbükeyliğinin ve içbükeyliğinin belirlenmesi. 8. Çalışmaya dayalı bir grafik oluşturmak, minimum veya maksimumu bulmanızı sağlar.

Ekstremumlarla çalışmak gerektiğinde ana unsur, grafiğinin tam yapısıdır. Okul öğretmenleri, eğitim sürecinin büyük bir ihlali olan bu kadar önemli bir hususa genellikle azami dikkat göstermezler. Grafik, yalnızca işlevsel verilerin çalışmasının sonuçlarına, keskin ekstremlerin tanımına ve grafikteki noktalara dayanarak oluşturulmuştur. Bir fonksiyonun türevinin keskin ekstremleri, asimptotları belirlemek için standart prosedür kullanılarak kesin değerlerin bir grafiğinde görüntülenir. Fonksiyonun maksimum ve minimum noktalarına daha karmaşık çizim eşlik eder. Bu, keskin bir ekstremum sorununu çözmek için daha derin bir ihtiyaçtan kaynaklanmaktadır. Ekstremum problemindeki en önemli kavramlardan biri olduğu için karmaşık ve basit bir fonksiyonun türevini bulmak da gereklidir.

fonksiyonel ekstremum

Yukarıdaki değeri bulmak için aşağıdaki kurallara uymalısınız:

• aşırı oran için gerekli koşulu belirlemek;
• grafikteki uç noktaların yeterli koşulunu dikkate alın;
• akut ekstremum hesaplamasını yapmak.

Zayıf minimum ve güçlü minimum gibi kavramlar da vardır. Bu, ekstremum ve kesin hesaplanması belirlenirken dikkate alınmalıdır. Aynı zamanda, keskin işlevsellik, işlev grafiğiyle çalışmak için gerekli tüm koşulların aranması ve oluşturulmasıdır.

Tanım 1. M noktasına (x 0; y 0) z \u003d f (x; y) fonksiyonunun maksimum (minimum) noktası denir, eğer M noktasının bir mahallesi varsa, tüm noktalar için (x; y) ) bu komşuluktan aşağıdaki eşitsizlik doğrudur:

f(x 0 ; y 0)  f(x; y), .

teorem 1 (ekstremumun varlığı için gerekli koşul) . Eğer türevlenebilir bir fonksiyon z = f(x; y) M(x 0 ; y 0) noktasında bir uç noktaya ulaşırsa, o zaman bu noktadaki birinci mertebeden kısmi türevleri sıfıra eşittir, yani.
;

Kısmi türevlerin sıfıra eşit olduğu noktalara denir. sabit veya kritik noktalar.

Teorem 2 (ekstremumun varlığı için yeterli koşul)

z = f(x; y) fonksiyonu olsun:

a) (x 0 ; y 0) noktasının bir komşuluğunda tanımlanır, burada
Ve
;

b) bu ​​noktada ikinci mertebeden sürekli kısmi türevlere sahiptir

;

O zaman, eğer  = AC  B 2 > 0 ise, (x 0; y 0) noktasında z = f(x; y) fonksiyonunun bir ekstremumu vardır, ayrıca A ise< 0 (или С < 0) – максимум, если А >0 (veya C > 0) minimumdur.  \u003d AC - B 2 olması durumunda< 0, функция z = f(x; y) экстремума не имеет. Если  = AC  B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).

örnek 1 z = x 2 + xy + y 2  3x  6y fonksiyonunun ekstremumunu bulun.

Çözüm. Birinci mertebeden kısmi türevleri bulalım:

Bir ekstremumun varlığı için gerekli koşulu kullanalım:

Denklem sistemini çözerek, durağan noktaların x ve y koordinatlarını buluruz: x = 0; y = 3, yani M(0; 3).

İkinci mertebenin kısmi türevlerini hesaplıyoruz ve değerlerini M noktasında buluyoruz.

bir =
= 2; C =
= 2;

B =
.

 = AC  B 2 = 2  2  1 > 0, A = 2 > 0 diskriminantını oluşturalım. Bu nedenle, M(0; 3) noktasında verilen fonksiyonun minimumu vardır. Fonksiyonun bu noktadaki değeri z min = -9'dur.

Fonksiyonların ekstremumlarını bulun

322. z = x 2 + y 2 + xy  4x  5y 323. z = y 3  x 3  3xy

324. z = x 2  2xy + 4y 3 325. z =
 y 2  x + 6y

326. z = x y (1  x  y) 327. z = 2xy  4x  2y

328. z = e  x/2 (x + y 2) 329. z = x 3 + 8y 3  6xy + 1

330. z = 3x 2 y  x 3  y 4 331. z = 3x + 6y  x 2  xy + y 2

Kapalı bir bölgedeki iki değişkenli bir fonksiyonun en büyük ve en küçük değerleri

Bulmak En büyük Ve en az kapalı bir alanda fonksiyon değerleri gereklidir:

1) verilen alanda bulunan kritik noktaları bulun ve bu noktalardaki fonksiyonun değerlerini hesaplayın;

2) bölgenin sınırındaki kritik noktaları bulun ve içindeki fonksiyonların maksimum ve minimum değerlerini hesaplayın;

3) bulunan tüm değerlerden en büyüğünü ve en küçüğünü seçin.

Örnek 2 z = fonksiyonunun en büyük ve en küçük değerlerini bulun
bir daire içinde x 2 + y 2  1.

Çözüm. z fonksiyonunun birinci mertebeden kısmi türevlerini hesapladığımız ve bunları sıfıra eşitlediğimiz, söz konusu bölge içinde bulunan kritik noktaların koordinatlarını bulalım.

x = 0, y = 0 ve dolayısıyla M(0; 0) kritik noktadır.

М(0; 0) noktasında z fonksiyonunun değerini hesaplayalım: z(0; 0) = 2.

Bölgenin sınırındaki kritik noktaları bulalım - x 2 + y 2 = 1 denklemiyle verilen daire. y 2 = 1 - x 2'yi z = z(x; y) fonksiyonuna koyarsak, bir fonksiyon elde ederiz. bir değişkenin

z=
;

ve x[1; 1].

türevi hesapladıktan sonra
ve onu sıfıra eşitleyerek, x 1 = 0, x 2 = bölgesinin sınırında kritik noktalar elde ederiz. , x 3 =

z(x) = fonksiyonunun değerini bulun
kritik noktalarda ve segmentin sonunda [-1; 1]: z(0) = ;
=;
; z(1) = ; z(1) =

Dairenin içinde ve sınırında bulunan kritik noktalarda z fonksiyonunun değerleri arasından en büyüğünü ve en küçüğünü seçiyoruz.

Yani, z maks. = z(0; 0) = 2

Optimizasyon problemlerinde ekstremumları bulmak gerekli hale gelir. iki veya daha fazla değişkenli fonksiyonlar denklemle verilen bu ilişkinin değişkenleri arasında bir ilişki olması şartıyla . Bu durumda, bulmamız gerektiğini söylüyoruz. koşullu ekstremum .

Koşullu ekstremumu bulmak için, kısmi türevler ve karar ver denklem sistemleriŞimdi bir örnek kullanarak analiz edeceğimiz üç adımdan oluşan bir koşullu ekstremum bulmak için bir algoritma ve bu örneği analiz ederken herkese ulaşması gereken koşullu ekstremumun geometrik anlamı var.

Bu nedenle, en yaygın problem örneğinde analiz edeceğimiz algoritma - iki değişkenli bir fonksiyonun koşullu ekstremumunu bulmak. .

Aşama 1. tanıtıldı Lagrange işlevi

burada ilk terim orijinal işlevin kendisidir ve eksi işaretli ikinci terim, bağlantı koşulu denkleminin sol tarafıdır, (lambda) - Lagrange çarpanı ile çarpılır.

örnek 1 Bulmak koşullu uçlar bir dikdörtgenin alanını kenarlarına göre ifade eden iki değişkenli bir fonksiyon x Ve y koşulu altında, yani bu dikdörtgeni bağlayabilecek bir ip var ve bu ipin uzunluğu 100'dür.

Aşama 1.Çözüm. Bağlantı koşulunun denklemini sağ tarafta sıfır olacak şekilde istenen forma getiriyoruz:

.

hadi besteleyelim Lagrange işlevi:

Adım 2 Eşitliklerden bir denklem sistemi oluşturuyoruz kısmi türevler sıfır ve bağlantı koşulunun denklemi (koşullu bir ekstremumun varlığının gerekli bir işareti):

Bu denklem sisteminin çözümleri, olası bir koşullu ekstremin noktalarıdır - durağan noktalar veya dedikleri gibi kritik noktalar.

Örnek 1. Adım 2.

Çözüm.

x Ve y :

Bu ifadeleri üçüncü denklemde yerine koyarız ve Lagrange çarpanının değerini buluruz:

x Ve y ve orijinal fonksiyonun değişkenlerinin değerlerini bulun:

alınan ve. Bu değerler aynı zamanda durağan noktanın koordinatlarıdır. Böylece durağan bir nokta elde ettik.

Aşama 3 2. adımda bulunan durağan nokta olsun. Koşullu ekstremin minimum mu yoksa maksimum mu olduğunu belirlemek için Lagrange fonksiyonunun ikinci diferansiyelini bulmamız gerekiyor.

ve ortaya çıkan ifadede, "lambda" değerini 2. adımda bulunan değerleriyle (Lagrange çarpanının değerleri) değiştirin.

Lagrange fonksiyonunun ikinci diferansiyelinin değeri sıfırdan () küçükse, durağan nokta maksimum noktadır, sıfırdan () büyükse, o zaman durağan nokta minimum noktadır. Lagrange fonksiyonunun ikinci diferansiyelinin değeri sıfıra eşitse, ek araştırma gereklidir, ancak bu tür durumlar öğrencilere verilen görevlerde pratik olarak ortaya çıkmaz.

Durağan noktaların koordinatları başlangıç ​​noktasına değiştirilir ve böylece sonunda buluruz. koşullu uçlar (veya minimum ve maksimum veya bu aşırı uçlardan biri).

Örnek 1. Adım 3.

Çözüm. Lagrange fonksiyonunun ikinci diferansiyelini bulun:

Bizim durumumuzda, birinci ve üçüncü bileşenler sıfıra eşit olduğundan, Lagrange çarpanının değerlerini bunlara ikame etmek zorunda değiliz. Ama farklar arasındaki ilişkiyi bulmanız gerekiyor. dx Ve ölmek :

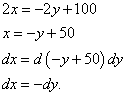
Elde edilen değerler ters işaretli olduğundan, her durumda bunu elde ederiz.

Şimdi değeri bulabiliriz koşullu ekstremum maksimum olan orijinal işlevin:

.

Bu, orijinal fonksiyon tarafından verilen dikdörtgenin uzunluğu 100 olan bir iple bağlanabilen maksimum alanıdır.

Örnek 2 Bulmak koşullu uçlar

Aşama 1. hadi besteleyelim Lagrange işlevi:

Adım 2 Lagrange fonksiyonunun kısmi türevlerini bulalım ve eşitliklerinden sıfıra bir denklem sistemi ve bağlantı koşulunun denklemini oluşturalım:

Birinci ve ikinci denklemlerden sırasıyla, x Ve y :

Bu ifadeleri üçüncü denklemde yerine koyuyoruz ve Lagrange çarpanının değerlerini buluyoruz:

Şimdi Lagrange çarpanının değerini şu ifadelerin yerine koyalım: x Ve y ve Lagrange çarpanının iki değeri için orijinal fonksiyonun değişkenlerinin değerlerini bulun:

Bu x ve y değerleri iki durağan noktanın koordinatlarıdır. Böylece durağan puanlar elde ettik. .

Aşama 3 Lagrange fonksiyonunun ikinci dereceden kısmi türevlerini bulun:

Lagrange fonksiyonunun ikinci diferansiyelini formüle göre bulun

:

Sıfırdan küçük bir değerimiz var, bu nedenle nokta nokta koşullu maksimum:

.

Lagrange fonksiyonunun ikinci diferansiyelinin işaretini Lagrange çarpanının değerine ayarlayın:

Sıfırdan büyük bir değer elde ettik, bu nedenle nokta noktadır. koşullu minimum:

.

Böylece, koşullu uçlar verilen fonksiyon bulunur.

Örnek 3 Bulmak koşullu uçlar koşul altında iki değişkenli fonksiyonlar.

Aşama 1. hadi besteleyelim Lagrange işlevi:

Adım 2 Lagrange fonksiyonunun kısmi türevlerini bulalım ve eşitliklerinden sıfıra bir denklem sistemi ve bağlantı koşulunun denklemini oluşturalım:

Birinci ve ikinci denklemlerden sırasıyla, x Ve y :

Ancak, değişkenlerin bu değerlerinin sistemin üçüncü denkleminde yer değiştirmesinin doğru eşitliği vermediğini anlıyoruz. Bu nedenle, aslında eşitliğin ikinci faktörünün sıfıra eşit olduğuna inanıyoruz: . Buradan alıyoruz

Lagrange çarpanının değerinde durağan noktaların koordinatlarını arıyoruz. Sonra denklem sisteminden x ve y için ifadelerden bunu takip eder. Sistemin üçüncü denkleminden elde ederiz.

Matematikte önemli bir kavram bir fonksiyondur. Onun yardımıyla doğada meydana gelen birçok işlemi görselleştirebilir, belirli miktarlar arasındaki ilişkiyi formüller, tablolar ve grafikler kullanarak bir grafik üzerinde yansıtabilirsiniz. Bir örnek, bir sıvı tabakasının bir gövde üzerindeki basıncının daldırma derinliğine, hızlanma - belirli bir kuvvetin bir nesne üzerindeki etkisine, sıcaklık artışına - iletilen enerjiye ve diğer birçok işleme bağımlılığıdır. Bir fonksiyonun incelenmesi, bir grafiğin oluşturulmasını, özelliklerinin açıklığa kavuşturulmasını, kapsam ve değerleri, artış ve azalma aralıklarını içerir. Bu süreçte önemli bir nokta ekstremum noktalarının bulunmasıdır. Nasıl doğru yapılacağı hakkında ve konuşma devam edecek.

Belirli bir örnekte kavramın kendisi hakkında

Tıpta, bir fonksiyon grafiğinin oluşturulması, hastanın vücudundaki hastalığın gelişiminin seyrini açık bir şekilde yansıtarak anlatabilir. Gün cinsinden zamanın OX ekseni boyunca çizildiğini ve insan vücudunun sıcaklığının OY ekseni boyunca çizildiğini varsayalım. Şekil, bu göstergenin nasıl keskin bir şekilde yükseldiğini ve ardından düştüğünü açıkça göstermektedir. Ayrıca, daha önce artmış olan fonksiyonun azalmaya başladığı ve bunun tersi olduğu anları yansıtan tekil noktaları fark etmek de kolaydır. Bunlar uç noktalardır, yani hastanın sıcaklığındaki bu durumda kritik değerler (maksimum ve minimum), sonrasında durumunda değişiklikler meydana gelir.

eğim açısı

Fonksiyonun türevinin nasıl değiştiğini şekilden belirlemek kolaydır. Grafiğin düz çizgileri zamanla yükselirse, o zaman pozitiftir. Ve ne kadar dik olursa, eğim açısı arttıkça türevin değeri o kadar büyük olur. Azalma dönemlerinde bu değer eksi değerler alarak uç noktalarda sıfıra döner ve ikinci durumda türevin grafiği OX eksenine paralel olarak çizilir.

Diğer tüm işlemler aynı şekilde ele alınmalıdır. Ancak bu kavramı anlatmanın en iyi yolu, grafiklerde açıkça gösterilen çeşitli cisimlerin hareketidir.

Hareket

Bir nesnenin düz bir çizgide hareket ettiğini ve düzgün bir şekilde hız kazandığını varsayalım. Bu süre boyunca, vücudun koordinatlarındaki değişiklik, bir matematikçinin parabolün bir dalı olarak adlandıracağı belirli bir eğriyi grafiksel olarak temsil eder. Aynı zamanda, koordinat göstergeleri her saniye daha hızlı ve daha hızlı değiştiği için fonksiyon sürekli artmaktadır. Hız grafiği, değeri de artan türevin davranışını gösterir. Bu, hareketin kritik noktaları olmadığı anlamına gelir.

Bu süresiz olarak devam edecekti. Ama ya vücut aniden yavaşlamaya, durmaya ve farklı bir yöne doğru hareket etmeye karar verirse? Bu durumda koordinat göstergeleri azalmaya başlayacaktır. Ve fonksiyon kritik bir değere geçecek ve artandan azalana dönüşecektir.

Bu örnekte, fonksiyonun grafiğindeki uç noktaların monoton olmaktan çıktığı anlarda göründüğünü tekrar anlayabilirsiniz.

Türevin fiziksel anlamı

Daha önce açıklananlar, türevin esasen fonksiyonun değişim oranı olduğunu açıkça gösterdi. Bu arıtma, fiziksel anlamını içerir. Uç noktalar, grafikteki kritik alanlardır. Sıfıra eşit olduğu ortaya çıkan türevin değerini hesaplayarak bunları bulmak ve tespit etmek mümkündür.

Bir ekstremum için yeterli bir koşul olan başka bir işaret var. Bu tür bükülme yerlerindeki türev, işaretini değiştirir: maksimum bölgesinde "+" dan "-" ye ve minimum bölgesinde "-" den "+" ye.

Yerçekimi etkisi altında hareket

Başka bir durum düşünelim. Top oynayan çocuklar, ufka doğru bir açıyla hareket etmeye başlayacak şekilde fırlattı. İlk anda, bu nesnenin hızı en büyüktü, ancak yerçekiminin etkisi altında azalmaya başladı ve her saniye aynı değerde, yaklaşık 9,8 m/sn2'ye eşit. Bu, serbest düşüş sırasında yerçekimi etkisi altında meydana gelen ivmenin değeridir. Ay'da, yaklaşık altı kat daha küçük olurdu.

Cismin hareketini açıklayan grafik, dalları aşağıyı gösteren bir paraboldür. Ekstremum noktaları nasıl bulunur? Bu durumda, bu, vücudun (top) hızının sıfır değerini aldığı fonksiyonun tepe noktasıdır. Fonksiyonun türevi sıfır olur. Bu durumda, yön ve dolayısıyla hızın değeri tersine değişir. Vücut her saniye daha hızlı ve daha hızlı uçar ve aynı miktarda hızlanır - 9.8 m/s 2 .

İkinci türev

Önceki durumda, hız modülünün grafiği düz bir çizgi olarak çizilmiştir. Bu miktarın değeri sürekli azaldığından, bu çizgi ilk önce aşağıya doğru yönlendirilir. Zamandaki noktalardan birinde sıfıra ulaştıktan sonra, bu değerin göstergeleri artmaya başlar ve hız modülünün grafiksel gösteriminin yönü önemli ölçüde değişir. Şimdi çizgi yukarıyı gösteriyor.

Koordinatın zamana göre türevi olan hız da kritik bir noktaya sahiptir. Bu bölgede başlangıçta azalan fonksiyon artmaya başlar. Bu, fonksiyonun türevinin uç noktasının yeridir. Bu durumda teğetin eğimi sıfır olur. Koordinatın zamana göre ikinci türevi olan ivme ise işareti “-”den “+”ya değiştirir. Ve tekdüze yavaştan hareket, eşit olarak hızlanır.

Hızlanma Grafiği

Şimdi dört rakam düşünün. Her biri, hızlanma gibi fiziksel bir niceliğin zaman içindeki değişiminin bir grafiğini gösterir. "A" durumunda, değeri pozitif ve sabit kalır. Bu, vücudun hızının, koordinatı gibi sürekli arttığı anlamına gelir. Cismin sonsuz uzun bir süre bu şekilde hareket edeceğini hayal edersek, koordinatın zamana bağımlılığını yansıtan fonksiyonun sürekli arttığı ortaya çıkacaktır. Bundan kritik bölgelerinin olmadığı sonucu çıkar. Ayrıca türevin grafiğinde, yani doğrusal olarak değişen bir hız üzerinde uç noktalar da yoktur.

Aynısı pozitif ve sürekli artan ivmeli "B" durumu için de geçerlidir. Doğru, koordinatlar ve hız grafikleri burada biraz daha karmaşık olacaktır.

Hızlanma sıfıra gittiğinde

Şekil "B"ye bakıldığında, vücudun hareketini karakterize eden tamamen farklı bir resim gözlemlenebilir. Hızı, dalları aşağıyı gösteren bir parabol olarak grafiksel olarak gösterilecektir. OX ekseni ile kesişene kadar ivmedeki değişimi tanımlayan satıra devam edersek ve dahası, ivmenin sıfıra eşit olduğu bu kritik değere kadar, nesnenin hızının artacağını hayal edebiliriz. giderek daha yavaş. Koordinat fonksiyonunun türevinin uç noktası, parabolün tam tepesinde olacak, bundan sonra vücut hareketin doğasını kökten değiştirecek ve farklı bir yönde hareket etmeye başlayacak.

İkinci durumda, "G", hareketin doğası kesin olarak belirlenemez. Burada sadece, incelenen bir dönem için hızlanma olmadığını biliyoruz. Bu, nesnenin yerinde kalabileceği veya hareketin sabit bir hızda gerçekleştiği anlamına gelir.

Koordinat toplama sorunu

Okulda cebir çalışırken sıklıkla karşılaşılan ve sınava hazırlanmak için teklif edilen görevlere geçelim. Aşağıdaki şekil fonksiyonun grafiğini göstermektedir. Ekstremum noktalarının toplamını hesaplamak gerekir.

Bunu y ekseni için fonksiyonun özelliklerinde değişiklik gözlemlenen kritik bölgelerin koordinatlarını belirleyerek yapacağız. Basitçe söylemek gerekirse, bükülme noktaları için x ekseni boyunca değerleri buluyoruz ve ardından ortaya çıkan terimleri eklemeye devam ediyoruz. Grafiğe göre, aşağıdaki değerleri aldıkları açıktır: -8; -7; -beş; -3; -2; 1; 3. Bu, cevap olan -21'e kadar ekler.

En uygun çözüm

Pratik görevlerin yerine getirilmesinde optimal çözümün seçiminin ne kadar önemli olabileceğini açıklamaya gerek yoktur. Sonuçta, hedefe ulaşmanın birçok yolu vardır ve kural olarak en iyi çıkış yolu sadece bir tanesidir. Bu, örneğin, bu insan yapımı nesnelerin en uygun biçimini bulmak için gemiler, uzay araçları ve uçaklar, mimari yapılar tasarlarken son derece gereklidir.

Araçların hızı, büyük ölçüde, su ve havada hareket ederken deneyimledikleri direncin, yerçekimi kuvvetlerinin ve diğer birçok göstergenin etkisi altında ortaya çıkan aşırı yüklenmelerin yetkin bir şekilde en aza indirilmesine bağlıdır. Denizdeki bir geminin fırtına sırasında stabilite gibi niteliklere ihtiyacı vardır; bir nehir gemisi için minimum su çekimi önemlidir. Optimal tasarımı hesaplarken, grafikteki uç noktalar, karmaşık bir problemin en iyi çözümü hakkında görsel olarak fikir verebilir. Böyle bir planın görevleri genellikle ekonomide, ekonomik alanlarda, diğer birçok yaşam durumunda çözülür.

eski tarihten

Aşırı görevler eski bilgeleri bile meşgul etti. Yunan bilim adamları, matematiksel hesaplamalar yoluyla alanların ve hacimlerin gizemini başarıyla çözdüler. Aynı çevreye sahip çeşitli şekillerden oluşan bir düzlemde dairenin her zaman en büyük alana sahip olduğunu ilk fark edenler onlardı. Benzer şekilde, bir top, aynı yüzey alanına sahip uzaydaki diğer nesneler arasında maksimum hacme sahiptir. Arşimet, Öklid, Aristoteles, Apollonius gibi ünlü şahsiyetler kendilerini bu tür sorunları çözmeye adadılar. Heron, hesaplamalara başvurarak ustaca cihazlar inşa eden ekstremum noktaları bulmada çok başarılı oldu. Bunlar arasında buharla hareket eden otomatik makineler, aynı prensipte çalışan pompalar ve türbinler vardı.

Kartaca İnşaatı

Komplosu aşırı görevlerden birini çözmeye dayanan bir efsane var. Bilgelerden yardım isteyen Fenike prensesinin gösterdiği iş yaklaşımının sonucu, Kartaca'nın inşasıydı. Bu eski ve ünlü şehrin arazisi, Afrika kabilelerinden birinin lideri tarafından Dido'ya (hükümdarın adıydı) sunuldu. Tahsis alanı ilk başta ona çok büyük görünmüyordu, çünkü sözleşmeye göre bir öküz derisi ile kaplanması gerekiyordu. Ancak prenses, askerlerine onu ince şeritler halinde kesmelerini ve onlardan bir kemer yapmalarını emretti. O kadar uzun olduğu ortaya çıktı ki, tüm şehrin sığabileceği bir alanı kapladı.

Kalkülüsün kökenleri

Ve şimdi eski çağlardan sonraki bir döneme geçelim. İlginç bir şekilde, 17. yüzyılda Kepler bir şarap satıcısıyla yaptığı görüşmede matematiksel analizin temellerini anlamaya yönlendirildi. Tüccar mesleğinde o kadar bilgiliydi ki, fıçıdaki içeceğin hacmini sadece demir bir turnike indirerek kolayca belirleyebiliyordu. Böyle bir merak üzerine düşünen ünlü bilim adamı, bu ikilemi kendisi çözmeyi başardı. O zamanların usta bakırcılarının, sabitleme halkalarının çevresinin belirli bir yüksekliğinde ve yarıçapında, maksimum kapasiteye sahip olacak şekilde kaplar yapma becerisine sahip oldukları ortaya çıktı.

Bu, Kepler için daha fazla düşünmek için bir fırsat oldu. Bochars, deneyimlerini nesilden nesile aktararak, uzun bir arayış, hatalar ve yeni girişimlerle en uygun çözüme ulaştı. Ancak Kepler, süreci hızlandırmak ve matematiksel hesaplamalarla kısa sürede nasıl yapılacağını öğrenmek istedi. Meslektaşları tarafından toplanan tüm gelişmeleri, şimdi bilinen Fermat ve Newton - Leibniz teoremlerine dönüştü.

Maksimum alanı bulma problemi

Uzunluğu 50 cm olan bir telimiz olduğunu hayal edin, ondan en büyük alana sahip bir dikdörtgen nasıl yapılır?

Bir karara başlamak, basit ve iyi bilinen gerçeklerden hareket etmelidir. Figürümüzün çevresinin 50 cm olacağı açıktır.Ayrıca her iki kenar uzunluğunun iki katından oluşmaktadır. Bu, birinin "X" olarak atanması durumunda diğerinin (25 - X) olarak ifade edilebileceği anlamına gelir.

Buradan X'e (25 - X) eşit bir alan elde ederiz. Bu ifade birçok değer alan bir fonksiyon olarak gösterilebilir. Problemin çözümü bunların maksimumunu bulmayı gerektirir, bu da ekstremum noktalarını bulmanız gerektiği anlamına gelir.

Bunu yapmak için birinci türevi bulup sıfıra eşitliyoruz. Sonuç basit bir denklemdir: 25 - 2X = 0.

Buradan, kenarlardan birinin X = 12.5 olduğunu öğreniyoruz.

Bu nedenle, başka bir: 25 - 12.5 \u003d 12.5.

Sorunun çözümünün 12,5 cm kenarlı bir kare olacağı ortaya çıktı.

Maksimum hız nasıl bulunur

Bir örnek daha düşünelim. Doğrusal hareketi S \u003d - t 3 + 9t 2 - 24t - 8 denklemi ile tanımlanan, kat edilen mesafenin metre cinsinden ifade edildiği ve zamanın saniye cinsinden ifade edildiği bir cisim olduğunu hayal edin. Maksimum hızı bulmak için gereklidir. Nasıl yapılır? İndirilen hızı, yani ilk türevi bulun.

Denklemi elde ederiz: V = - 3t 2 + 18t - 24. Şimdi, sorunu çözmek için yine ekstremum noktalarını bulmamız gerekiyor. Bu, önceki görevdekiyle aynı şekilde yapılmalıdır. Hızın ilk türevini bulup sıfıra eşitliyoruz.

Şunu elde ederiz: - 6t + 18 = 0. Dolayısıyla t = 3 s. Bu, vücudun hızının kritik bir değer aldığı zamandır. Elde edilen verileri hız denkleminde yerine koyarız ve şunu elde ederiz: V = 3 m/s.

Ancak bunun tam olarak maksimum hız olduğu nasıl anlaşılır, çünkü işlevin kritik noktaları en büyük veya en küçük değerler olabilir? Kontrol etmek için hızın ikinci türevini bulmanız gerekir. Eksi işareti ile 6 sayısı olarak ifade edilir. Bu, bulunan noktanın maksimum olduğu anlamına gelir. Ve ikinci türevin pozitif bir değeri olması durumunda, bir minimum olacaktır. Dolayısıyla bulunan çözüm doğruydu.

Örnek olarak verilen görevler, bir fonksiyonun uç noktalarını bularak çözülebileceklerin sadece bir kısmıdır. Aslında, çok daha fazlası var. Ve bu tür bilgi, insan uygarlığı için sınırsız olanaklar açar.

İşlev y = f(x) denir artan (azalan) eğer x 1 için bir aralıkta< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).

Bir segmentteki türevlenebilir bir fonksiyon y \u003d f (x) artarsa ​​(azalırsa), o zaman bu segmentteki türevi f " (x )> 0

(F"(x)< 0).

Nokta x hakkında isminde yerel maksimum nokta (asgari) fonksiyonunun f (x ) noktasının bir komşuluğu varsa x o, eşitsizliği f (x) olan tüm noktalar için≤ f (x o) (f (x)≥ f(xo)).

Maksimum ve minimum noktalar denir uç noktalar, ve bu noktalardaki fonksiyonun değerleri onun aşırılık.

uç noktalar

Ekstremum için gerekli koşullar . Eğer nokta x hakkında f (x) fonksiyonunun bir uç noktasıdır, o zaman ya f " (x o ) = 0 veya f(x o ) yok. Bu tür noktalara denir kritik, burada fonksiyonun kendisi kritik noktada tanımlanır. Bir fonksiyonun uç noktaları, kritik noktaları arasında aranmalıdır.

İlk yeterli koşul. İzin vermek x hakkında - kritik nokta. Eğer f" (x ) noktadan geçerken x hakkında artı işaretini eksi olarak değiştirir, ardından noktada x o fonksiyonun bir maksimumu vardır, aksi takdirde bir minimumu vardır. Kritik bir noktadan geçerken türev işaret değiştirmiyorsa, o noktada x hakkında ekstremum yoktur.

İkinci yeterli koşul. f(x) fonksiyonuna sahip olsun
F" (x ) noktanın yakınında x hakkında ve ikinci türev f "" (x 0) tam noktada x o. Eğer f"(x o) = 0, f "" (x 0)>0 (f "" (x 0)<0), то точка x o f(x) fonksiyonunun yerel minimum (maksimum) noktasıdır. Eğer f "" (x 0) = 0 ise, o zaman ya ilk yeterli koşulu kullanmanız ya da daha yüksek olanları dahil etmeniz gerekir.

Bir segmentte, y \u003d f (x) işlevi, kritik noktalarda veya segmentin uçlarında en küçük veya en büyük değere ulaşabilir.

Örnek 3.22.

Çözüm.Çünkü F " (

Bir fonksiyonun ekstremumunu bulmak için görevler

Örnek 3.23. a

Çözüm. x Ve y y
0 ≤ x≤
> 0, iken x >a/4S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение fonksiyonlar metrekare. birimler).

Örnek 3.24. p ≈

Çözüm. kişi
S"
R = 2, H = 16/4 = 4.

Örnek 3.22.f (x) = 2x 3 - 15x 2 + 36x - 14 fonksiyonunun ekstremumunu bulun.

Çözüm.Çünkü F " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), ardından x 1 \u003d 2 ve x 2 \u003d 3. fonksiyonunun kritik noktaları puan. x 1 \u003d 2 noktasından geçerken, türev işareti artıdan eksiye değiştirdiğinden, bu noktada fonksiyonun bir maksimumu vardır. x 2 \u003d 3 noktasından geçerken, türev işareti eksiden artıya değiştirir, bu nedenle x 2 \u003d 3 noktasında fonksiyonun bir minimumu vardır. Fonksiyonun değerlerinin puan cinsinden hesaplanması
x 1 = 2 ve x 2 = 3, fonksiyonun ekstremumunu buluruz: maksimum f (2) = 14 ve minimum f (3) = 13.

Örnek 3.23.Taş duvarın yanına, üç tarafı tel örgü ile çevrilecek ve dördüncü tarafta duvara bitişik olacak şekilde dikdörtgen bir alan inşa etmek gerekir. Bunun için var aızgara lineer metre. Site hangi en-boy oranında en geniş alana sahip olacak?

Çözüm.aracılığıyla sitenin yanlarını belirtin x Ve y. Sitenin alanı S = xy'ye eşittir. İzin vermek y duvara bitişik kenarın uzunluğudur. O halde koşula göre 2x + y = a eşitliği sağlanmalıdır. Bu nedenle y = a - 2x ve S = x (a - 2x), burada
0 ≤ x≤ a /2 (pedin uzunluğu ve genişliği negatif olamaz). S "= a - 4x, a - 4x = 0 için x = a/4, nereden
y \u003d a - 2 × a / 4 \u003d a / 2. kadarıyla x = a/4 tek kritik nokta, bu noktadan geçerken türevin işaretinin değişip değişmediğini kontrol edelim. xa/4S için"> 0, iken x >a/4S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение fonksiyonlar S(a/4) = a/4(a - a/2) = bir 2/8 (metrekare. birimler). S sürekli olduğu ve S(0) ve S(a/2) uçlarındaki değerleri sıfıra eşit olduğu için bulunan değer fonksiyonun en büyük değeri olacaktır. Böylece, problemin verilen koşulları altında sitenin en uygun en boy oranı y = 2x'tir.

Örnek 3.24.V=16 kapasiteli kapalı silindirik tank yapılması gerekmektedir. p ≈ 50 m3 Üretiminde en az miktarda malzeme kullanmak için tankın boyutları (yarıçap R ve yükseklik H) ne olmalıdır?

Çözüm.Silindirin toplam yüzey alanı S = 2'dir. P R(R+H). Silindirin hacmini biliyoruz V = p R 2 N Þ N \u003d V / p R 2 \u003d 16 p / p R2 \u003d 16 / R2. O halde S(R) = 2 P (R2+16/R). Bu fonksiyonun türevini buluruz:
S"(R) \u003d 2 p (2R- 16 / R 2) \u003d 4 p (R- 8 / R 2). S" (R) = 0, R3 = 8 için, bu nedenle,
R = 2, H = 16/4 = 4.