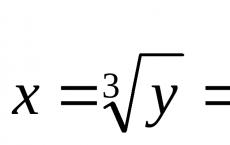ماذا تعني مجموعة القيم الوظيفية. نطاق الوظيفة (مجموعة قيم الوظائف)

ذ = س 3

ص=| س|

ص=

ه( ذ) = [- 1, 1]

ه( ذ) = (– ∞, + ∞)

ه( ذ) = (– ∞, + ∞)

ه( ذ) = (– ∞, + ∞)

ه( ذ) = (0, + ∞)

مقدمة لخوارزمية حل مسائل إيجاد مجموعة قيم الدوال المثلثية.

دعونا نرى كيف يمكننا تطبيق خبرتنا على المهام المختلفة المضمنة في الخيارات الخاصة باختبار واحد.

1. العثور على قيم الدوال لقيمة معينة للوسيطة.

مثال.أوجد قيمة الدالة y = 2 كوس(π/2+ π/4 ) – 1, لو س = -π/2.

حل.

= –
– 1.

2. إيجاد مدى الدوال المثلثية


حل.

1≤ خطيئةX≤ 1

2 ≤ 2 خطيئةX≤ 2

9 ≤ 11+2خطيئةX≤ 13

3 ≤
+2∙ خطيئةس ≥
، أي. ه (ص) = .

دعونا نكتب القيم الصحيحة للدالة على الفاصل الزمني. هذا الرقم هو 3.

الجواب: 3.

• 
  أوجد مجموعة قيم الدالة في= الخطيئة 2 X+6خطيئة X + 10.

• 
  أوجد مجموعة قيم الدالة: في = خطيئة 2 X - 6 خطيئة س + 8 . (على المرء)

في= خطيئة 2 X- 2 3 خطيئةس + 3 2 - 3 2 + 8,

في= (خطيئةX- 3) 2 -1.

ه ( خطيئةX) = [-1;1];

ه ( خطيئةX -3) = [-4;-2];

ه ( خطيئةX -3) 2 = ;

ه ( في) = .

إجابة: .

• 
  أوجد أصغر قيمة للدالة في= كوس 2 س+2خطيئة س – 2.

هل يمكننا إيجاد مجموعة من القيم لهذه الدالة؟ (لا.)

ما الذي يجب إتمامه؟ (تم تقليله إلى وظيفة واحدة.)

كيف افعلها؟ (استخدم الصيغة cos 2 س= 1-الذنب 2 س.)

لذا، في= 1-الذنب 2 س+2خطيئة س –2,

ذ= -الخطيئة 2 س+2خطيئة س –1,

في= -(خطيئة س –1) 2 .

حسنًا، الآن يمكننا إيجاد مجموعة من القيم واختيار الأصغر منها.

1 ≥ الخطيئة س ≤ 1,

2 ≥ الخطيئة س – 1 ≤ 0,

0 ≥ (الخطيئة س – 1) 2 ≤ 4,

4 ≥ -(خطيئة س -1) 2 ≤ 0.

إذن أصغر قيمة للدالة في يؤجر= -4. الجواب: -4.

• 
  ابحث عن حاصل ضرب أكبر وأصغر قيم للدالة

حل.

في= 1-كوس 2 س+ كوس س + 1,5,

في= -كوس 2 س+ 2∙0.5∙cos س - 0,25 + 2,75,

في= -(كوس س- 0,5) 2 + 2,75.

ه(كوس س) = [-1;1],

ه(كوس س – 0,5) = [-1,5;0,5],

ه(كوس س – 0,5) 2 = ,

ه(-(كوس س-0,5) 2) = [-2,25;0],

ه( في) = .

أكبر قيمة للدالة في naib= 2.75؛ أصغر قيمة في يؤجر= 0.5. لنجد حاصل ضرب القيمة الأكبر والأصغر للدالة:

في naib ∙في يؤجر = 0,5∙2,75 = 1,375.

الجواب: 1.375.

دعونا نعيد كتابة الوظيفة في النموذج في =,

في =
,

دعونا الآن نجد مجموعة قيم الدالة.

ه(الخطيئة س) = [-1, 1],

ه(6الخطيئة س) = [-6, 6],

ه(6الخطيئة س + 1) = [-5, 7],

ه ((6خطيئة س + 1) 2) = ,

ه(- (6الخطيئة س + 1) 2) = [-49, 0],

ه(- (6الخطيئة س + 1) 2 + 64) = ,

ه( ذ) = [
, 8].

لنجد مجموع القيم الصحيحة للدالة: 4 + 5 + 6 + 7 + 8 = 30.

الجواب: 30.

1)
إنه Xينتمي إلى الربع الأول.

2)

ولذلك، 2 Xتنتمي إلى الربع الثاني.

3) في الربع الثاني تتناقص دالة الجيب وتكون مستمرة. إذن هذه الوظيفة
يأخذ كل القيم من
قبل

4) احسب هذه القيم:

إجابة :
.

1) بما أن الجيب يأخذ القيم من -1 إلى 1، فإن مجموعة قيم الفرق
. عندما تتضاعف
سوف يذهب هذا الجزء إلى الجزء
.

2) الأركوسين هو دالة متناقصة ومستمرة بشكل رتيب. وبالتالي فإن مجموعة قيم التعبير هي قطعة
.

3) عند ضرب هذا الجزء ب نحن نحصل
.

إجابة:
.

بما أن قوس الظل هو دالة متزايدة، إذن
.

2) عند الزيادة Xمن
قبل الحجة 2 Xيزيد من
قبل . بما أن جيب الجيب في مثل هذه الفترة يزداد، فإن الدالة
يأخذ القيم من
تصل إلى 1.

3) عند الزيادة من قبل
الحجة 2 Xيزيد من قبل
. بما أن جيب الجيب يتناقص في مثل هذه الفترة، فإن الدالة
يأخذ القيم من
تصل إلى 1.

4) باستخدام صيغة التعبير عن الجيب بدلالة ظل نصف الزاوية نجد ذلك

.

ومن ثم فإن مجموعة القيم المطلوبة هي اتحاد الأجزاء
و
، أي المقطع
.

إجابة:
.
تستخدم هذه التقنية (إدخال زاوية مساعدة) لإيجاد مجموعة قيم دوال الشكل

في= خطيئة س + ب كوس سأو في= ذنب (رس) + بكوس (رس).

• 
  أوجد مجموعة قيم الدالة

حل.

دعونا نجد القيمة
=
= 25.

دعونا تحويل التعبير

15 جا 2س + 20 جتا 2س = 25 (
) = 25 () =

25 خطيئة (2x + )، حيث كوس = الخطيئة =.

مجموعة قيم الدالة y \u003d sin (2x + ): -1 الخطيئة (2x + ) 1.

ثم مجموعة قيم الدالة الأصلية -25 25 خطيئة (2x + ) 25.

إجابة: [-25; 25].
3. مهام العثور على أكبر وأصغر قيم للدالة على الفاصل الزمني.

• 
  أوجد أكبر وأصغر قيمة للدالة في= ط م Xعلى المقطع [π/4; π/2].

وظيفة في= ط م Xيتناقص على المقطع [π/4; π/2]، وبالتالي فإن الدالة سوف تأخذ أصغر قيمة عند س =π/2، أي في(π/2) = сtg π/2 = 0; وأكبر قيمة هي في س=π/4، أي في(π/4) = π/4 = 1.

الجواب: 1، 0.

منفصلة في المساواة
الجزء الكامل: .

ويترتب على ذلك أن الرسم البياني للدالة f(x) هو إما قطع زائد (а≠ 0) أو خط مستقيم بدون نقطة.

علاوة على ذلك، إذا كان أ؛ 2 أ) و (2 أ؛
) وإذا كانت a > 0، فإنها تزداد رتابة على هذه الأشعة.

إذا كانت a \u003d 0، ثم f (x) \u003d -2 على كامل مجال التعريف x ≠ 0. لذلك، من الواضح أن القيم المطلوبة للمعلمة لا تساوي الصفر.

نظرًا لأننا مهتمون فقط بقيم الوظيفة في المقطع [-1؛ 1]، ثم يتم تحديد تصنيف المواقف من خلال حقيقة أن الخط المقارب x = 2a للقطع الزائد (a≠0) يقع بالنسبة إلى هذا الجزء.

الحالة 1. جميع نقاط الفاصل الزمني [-1؛ 1] على يمين الخط المقارب العمودي x = 2a، أي عندما يكون 2a

الحالة 2. الخط المقارب العمودي يتقاطع مع الفاصل الزمني [-1؛ 1]، وتتناقص الدالة (كما في الحالة 1)، أي متى

الحالة 3. الخط المقارب العمودي يتقاطع مع الفاصل الزمني [-1؛ 1] والدالة متزايدة، أي -1

.

الحالة 4. جميع نقاط الفاصل الزمني [-1؛ 1] على يسار الخط المقارب العمودي، أي 1 أ > . والثانية
الاستقبال 4 . التعبير عن x بدلالة y. (إيجاد مجال الدالة العكسية)

الاستقبال 5.تبسيط الصيغة التي تحدد دالة عقلانية كسرية

الاستقبال 6.العثور على مجموعة من القيم وظائف تربيعية(من خلال إيجاد رأس القطع المكافئ وتحديد طبيعة سلوك فروعه).

الاستقبال 7.إدخال زاوية مساعدة لإيجاد مجموعة قيم بعض الدوال المثلثية.

صفحة 1

يسمى اعتماد متغير واحد على آخر التبعية الوظيفيةالتبعية المتغيرة ذمن متغير سمُسَمًّى وظيفة، إذا كانت كل قيمة سيطابق قيمة واحدة ذ.

تعيين:

عامل سيسمى المتغير المستقل أو دعوى، والمتغير ذ- متكل. ويقولون ان ذهي وظيفة س. معنى ذالمقابلة للقيمة المحددة س، مُسَمًّى قيمة الوظيفة.

كل القيم التي يتطلبها س، استمارة نطاق الوظيفة; كل القيم التي يتطلبها ذ، استمارة مجموعة من القيم الوظيفية.

التسميات:

د(و)- قيم الوسيطة. ه(و)- القيم الوظيفية. إذا تم إعطاء الدالة بواسطة صيغة، فيعتبر أن مجال التعريف يتكون من جميع قيم المتغير الذي تكون هذه الصيغة منطقية له.

الرسم البياني الوظيفييتم استدعاء مجموعة جميع النقاط على المستوى الإحداثي ، والتي تساوي حروفها قيم الوسيطة ، والإحداثيات تساوي القيم المقابلة للدالة. إذا كانت بعض القيمة س=س0مطابقة قيم متعددة (وليس واحدة فقط) ذ، فإن مثل هذه المراسلات ليست وظيفة. لكي تكون مجموعة نقاط المستوى الإحداثي رسمًا بيانيًا لوظيفة ما، فمن الضروري والكافي أن يتقاطع أي خط مستقيم موازٍ لمحور Oy مع الرسم البياني عند نقطة واحدة فقط.

طرق ضبط الوظيفة

1) يمكن ضبط الوظيفة تحليليافي شكل صيغة. على سبيل المثال،

2) يمكن تعريف الوظيفة من خلال جدول مكون من عدة أزواج (س؛ ص).

3) يمكن ضبط الوظيفة بيانيا. أزواج القيمة (س؛ ص)يتم عرضها على المستوى الإحداثي.

رتابة الوظيفة

وظيفة و (خ)مُسَمًّى في ازديادعلى فاصل رقمي محدد، إذا كانت القيمة الأكبر للوسيطة تتوافق مع قيمة أكبر للدالة. تخيل أن نقطة معينة تتحرك على طول الرسم البياني من اليسار إلى اليمين. بعد ذلك سوف تقوم النقطة بنوع من "الصعود" إلى أعلى الرسم البياني.

وظيفة و (خ)مُسَمًّى يتضاءلعلى فاصل رقمي معين، إذا كانت القيمة الأكبر للوسيطة تتوافق مع قيمة أصغر للدالة. تخيل أن نقطة معينة تتحرك على طول الرسم البياني من اليسار إلى اليمين. بعد ذلك سوف "تتدحرج" النقطة إلى أسفل المخطط.

تسمى الدالة التي تكون متزايدة أو تتناقص فقط خلال فترة رقمية معينة رتيبفي هذه الفترة.

وظيفة الأصفار وفترات الثبات

قيم X، الذي ص=0، يسمى وظيفة الأصفار. هذه هي حدود نقاط تقاطع الرسم البياني للدالة مع المحور السيني.

مثل هذه النطاقات من القيم س، والتي عليها قيم الدالة ذيتم استدعاء إما الإيجابية فقط أو السلبية فقط فترات ثبات الإشارة للدالة.

وظائف زوجية وغريبة

دالة زوجية
1) مجال التعريف متماثل بالنسبة للنقطة (0؛ 0)، أي إذا كانت النقطة أينتمي إلى مجال التعريف، ثم هذه النقطة -أينتمي أيضًا إلى مجال التعريف.
2) لأي قيمة س و(-س)=و(خ)
3) الرسم البياني للدالة الزوجية متماثل حول محور أوي.

وظيفة غريبةلديه الخصائص التالية:
1) مجال التعريف متماثل بالنسبة للنقطة (0؛ 0).
2) لأي قيمة س، الذي ينتمي إلى مجال التعريف، المساواة و(-س)=-و(خ)
3) الرسم البياني للدالة الفردية متماثل بالنسبة إلى الأصل (0؛ 0).

ليست كل دالة زوجية أو فردية. المهام منظر عام ليست حتى ولا غريبة.

وظائف دورية

وظيفة Fيسمى دوريًا إذا كان هناك رقم مثل هذا لأي سمن مجال تعريف المساواة و(س)=و(س-T)=و(س+T). تهي فترة الوظيفة.

كل دالة دورية لها عدد لا نهائي من الفترات. ومن الناحية العملية، عادة ما تؤخذ في الاعتبار أصغر فترة إيجابية.

تتكرر قيم الدالة الدورية بعد فترة تساوي هذه الفترة. يتم استخدامه عند رسم الرسوم البيانية.

د(و)- تلك القيم التي يمكن أن تتخذها الحجة، أي نطاق الوظيفة.

ه(و)- تلك القيم التي يمكن أن تأخذها الدالة، أي مجموعة من القيم الوظيفية.

طرق العثور على نطاقات الوظائف.

البحث المتسلسل لقيم وسيطات الوظائف المعقدة؛

طريقة التسجيل/الحدود؛

استخدام خصائص الاستمرارية ورتابة الوظيفة؛

استخدام مشتق.

باستخدام أكبر وأصغر قيم الدالة؛

الطريقة الرسومية

طريقة إدخال المعلمة؛

طريقة الدالة العكسية

دعونا نفكر في بعض منهم.

باستخدام المشتقة

النهج العاملإيجاد مجموعة قيم الدالة المستمرة f(x) هو العثور على أكبر وأصغر قيم للدالة f(x) في مجالها (أو إثبات عدم وجود أحدهما أو كليهما) .

إذا كنت بحاجة إلى العثور على مجموعة قيم الوظيفة على الجزء:

أوجد مشتقة الدالة المعطاة f "(x);

ابحث عن النقاط الحرجة للدالة f(x) واختر تلك التي تنتمي إلى المقطع المحدد؛

حساب قيم الوظيفة في نهايات المقطع وعند النقاط الحرجة المحددة؛

من بين القيم التي تم العثور عليها، حدد القيم الأصغر والأكبر؛

يتم الانتهاء من مجموعة القيم الوظيفية بين هذه القيم.

إذا كان نطاق الوظيفة هو فاصلة، ثم يتم استخدام نفس المخطط، ولكن بدلاً من القيم الموجودة في النهايات، يتم استخدام حدود الدالة عندما يميل الوسيط إلى نهايات الفاصل الزمني. القيم الحدية من غير مضمنة في مجموعة القيم.

طريقة الحدود/النتيجة

للعثور على مجموعة قيم الدالة، ابحث أولاً عن مجموعة قيم الوسيطات، ثم ابحث عن القيم الدنيا والقصوى المقابلة لوظيفة الدالة. استخدام عدم المساواة - تحديد الحدود.

والجوهر هو تقدير الدالة المستمرة من الأسفل ومن الأعلى وإثبات أن الدالة تصل إلى الحدود الدنيا والعليا للتقديرات. وفي هذه الحالة يتم تحديد تزامن مجموعة قيم الدالة مع الفاصل الزمني من الحد الأدنى للتقدير إلى الحد الأعلى من خلال استمرارية الدالة وغياب قيم أخرى لها.

خواص الدالة المستمرة

هناك خيار آخر وهو تحويل الدالة إلى دالة رتيبة مستمرة، ثم باستخدام خصائص المتباينات، يتم تقدير مجموعة قيم الدالة التي تم الحصول عليها حديثًا.

البحث بشكل متسلسل عن قيم وسيطات الوظائف المعقدة

بناءً على البحث المتسلسل عن مجموعة قيم الدوال الوسيطة التي تتكون منها الدالة

نطاقات الوظائف الأولية الأساسية

أمثلة

أوجد مجموعة قيم الدالة:

باستخدام المشتقة

ابحث عن مجال التعريف: D(f)=[-3;3]، لأن $9-x^(2)\geq 0$

أوجد المشتقة: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$

f"(x) = 0 إذا x = 0. f"(x) غير موجود إذا كان $\sqrt(9-x^(2))=0$، أي لـ x = ±3. نحصل على ثلاث نقاط حرجة: x 1 \u003d -3، x 2 \u003d 0، x 3 \u003d 3، اثنتان منها تتزامن مع نهايات المقطع. احسب: f(–3) = 0، f(0) = 3، f(3) = 0. وبالتالي، أصغر قيمة لـ f(x) هي 0، وأكبر قيمة هي 3.

الإجابة: ه(و) = .

عدم استخدام المشتقة

ابحث عن القيم الأكبر والأصغر للدالة:

منذ $
و(س) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ ، ثم:

$f(x)\leq \frac(3)(4)$ لكل x;

$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ لجميع x(لأن $|\cos (خ)|\leq 1$);

$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;

$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;

الإجابة: $\frac(3)(4)$ و$-\frac(3)(2)$

إذا قمت بحل هذه المشكلة بمساعدة المشتقات، فستحتاج إلى التغلب على العقبات المرتبطة بحقيقة أن الوظيفة f (x) محددة ليس على قطعة، ولكن على الخط الحقيقي بأكمله.

استخدام طريقة الحدود/التقديرات

ويترتب على تعريف الجيب أن $-1\leq\sin(x)\leq 1$. بعد ذلك، نستخدم خصائص المتباينات العددية.

$-4\leq - 4\sin(x)\leq 4$، (اضرب الأجزاء الثلاثة للمتباينة المزدوجة في -4)؛

$1\leq 5 - 4\sin(x)\leq 9$ (يضاف إلى الأجزاء الثلاثة للمتباينة المزدوجة 5)؛

وبما أن هذه الدالة متصلة على كامل مجال التعريف فإن مجموعة قيمها تقع بين قيمتها الأصغر والأكبر على كامل مجال التعريف إن وجدت.

في هذه الحالة، مجموعة قيم الدالة $y = 5 - 4\sin(x)$ هي المجموعة .

من المتباينات $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ نحصل على التقدير $$\\ -6\leq y\ ليك 6$$

بالنسبة لـ x = p وx = 0، تأخذ الدالة القيمتين -6 و6، أي. يصل إلى الحدود الدنيا والعليا. كمجموعة خطية من الدوال المستمرة cos(7x) وcos(x)، فإن الدالة y مستمرة على طول محور العدد الصحيح، وبالتالي، من خلال خاصية الدالة المستمرة، فإنها تأخذ جميع القيم من -6 إلى 6 شاملة ، وهم فقط، لأنه بسبب عدم المساواة $- 6\leq y\leq 6$ فإن القيم الأخرى مستحيلة لذلك.

وبالتالي، E(y) = [-6;6].

$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ الإجابة: E(f) = .

$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

دعونا نحول التعبير $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ((\ فارك(x + \frac(\pi)(2) - x)(2)) \يمين)\cos\left ((\frac(x + \frac(\pi)(2) + x)( 2)) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.

تعريف جيب التمام يعني $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$

وبما أن هذه الدالة متصلة على كامل مجال التعريف فإن مجموعة قيمها تقع بين قيمتها الأصغر والأكبر إن وجدت، مجموعة قيم الدالة $y =\sqrt(2)\ cos((x +\frac(\pi)(4 )))$ هي المجموعة $[-\sqrt(2);\sqrt(2)]$.

$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$

تشير إلى $t = 5 – (3^(x)+1)^(2)$، حيث -∞≥t≥4. وهكذا تتلخص المشكلة في إيجاد مجموعة قيم الدالة $y = \log_(0,5)(t)$ على الشعاع (-∞;4). نظرًا لأن الدالة $y = \log_(0,5)(t)$ محددة فقط من أجل t > 0 ، فإن مجموعة قيمها على الشعاع (-∞;4) تتزامن مع مجموعة قيم الدالة على الفاصل الزمني (0;4) تمثل تقاطع الشعاع (-∞;4) مع مجال التعريف (0;+∞) للدالة اللوغاريتمية. في الفترة (0;4) تكون هذه الدالة مستمرة ومتناقصة. بالنسبة لـ t > 0، فإنها تميل إلى +∞، وبالنسبة لـ t = 4 فإنها تأخذ القيمة -2، لذا فإن E(y) = (-2، +∞).

نحن نستخدم تقنية تعتمد على التمثيل الرسومي للوظيفة.

بعد تحويلات الدالة، لدينا: y 2 + x 2 = 25، و y ≥ 0, |x| ≥ 5.

يجب أن نتذكر أن $x^(2)+y^(2)=r^(2)$ هي معادلة دائرة نصف قطرها r.

في ظل هذه القيود، الرسم البياني لهذه المعادلة هو نصف الدائرة العلوي المتمركز عند نقطة الأصل ونصف القطر يساوي 5. ومن الواضح أن E(y) = .

الإجابة: ه(ذ) = .

مراجع

نطاق الوظائف في استخدام المهام، مينيوك إيرينا بوريسوفنا

نصائح للعثور على مجموعة قيم الوظائف، Belyaeva I.، Fedorova S.

إيجاد مجموعة قيم الدالة

كيفية حل المشكلات في الرياضيات في امتحانات القبول، I. I. Melnikov، I. N. Sergeev

الوظيفة هي النموذج دعونا نعرّف X على أنها مجموعة قيم لمتغير مستقل // يعني أي مستقل.

الدالة هي قاعدة يمكن من خلالها، لكل قيمة للمتغير المستقل من المجموعة X، إيجاد القيمة الوحيدة للمتغير التابع. // أي. لكل x يوجد y واحد.

يترتب على التعريف أن هناك مفهومين - متغير مستقل (نشير إليه بـ x ويمكن أن يأخذ أي قيمة) ومتغير تابع (نشير إليه بـ y أو f (x) ويتم حسابه من الدالة عندما نستبدل x).

على سبيل المثال ص=5+س

1. المستقل هو x، لذلك نأخذ أي قيمة، دع x = 3

2. والآن نحسب y، إذن y \u003d 5 + x \u003d 5 + 3 \u003d 8. (y يعتمد على x، لأن ما x نستبدله، نحصل على y)

نقول أن المتغير y يعتمد وظيفيا على المتغير x ويرمز لذلك كما يلي: y = f (x).

على سبيل المثال.

1.ص=1/س. (يسمى مبالغة)

2.ص=س^2. (يسمى القطع المكافئ)

3.ص=3س+7. (يسمى الخط المستقيم)

4. ص \u003d √ س. (ويسمى فرع القطع المكافئ)

المتغير المستقل (الذي نشير إليه بـ x) يسمى وسيطة الدالة.

نطاق الوظيفة

مجموعة جميع القيم التي تأخذها وسيطة الدالة تسمى مجال الدالة ويشار إليها بـ D(f) أو D(y).

خذ بعين الاعتبار D(y) لـ 1.,2.,3.,4.

1. D (y)= (∞; 0) و (0;+∞) // المجموعة الكاملة للأعداد الحقيقية باستثناء الصفر.

2. D (y) \u003d (∞; +∞) // جميع الأعداد الحقيقية العديدة

3. D (y) \u003d (∞; +∞) // جميع الأعداد الحقيقية العديدة

4. د (ص) \u003d)