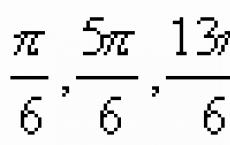Inverzne trigonometrijske funkcije i njihovi grafovi. Šta je arcsin, arkosinus? Šta je arc tangenta, arc tangenta? Članak inverzne trigonometrijske funkcije

U nizu zadataka matematike i njene primjene, potrebno je, iz poznate vrijednosti trigonometrijske funkcije, pronaći odgovarajuću vrijednost ugla, izraženu u stepenima ili radijanima. Poznato je da ista vrijednost sinusa odgovara beskonačnom broju uglova, na primjer, ako je $\sin α=1/2,$ onda ugao $α$ može biti jednak i $30°$ i $150°, $ ili u radijanskim mjerama $π /6$ i $5π/6,$ i bilo koji od uglova dobijenih iz njih dodavanjem člana u obliku $360°⋅k,$ odnosno $2πk,$ gdje je $k$ bilo koji cijeli broj. Ovo postaje jasno iz razmatranja grafika funkcije $y=\sin x$ na cijeloj brojevnoj pravoj (vidi sliku $1$): ako na osi $Oy$ nacrtamo segment dužine $1/2$ i nacrtamo prava paralelna sa $Ox osom, $ tada će preseći sinusoidu u beskonačnom broju tačaka. Kako bi se izbjegla moguća raznolikost odgovora, uvode se inverzne trigonometrijske funkcije, inače zvane kružne, ili lučne funkcije (od latinske riječi arcus - "luk").

Četiri osnovne trigonometrijske funkcije $\sin x,$ $\cos x,$ $\mathrm(tg)\,x$ i $\mathrm(ctg)\,x$ odgovaraju četiri lučne funkcije $\arcsin x,$ $\arccos x ,$ $\mathrm(arctg)\,x$ i $\mathrm(arcctg)\,x$ (čitaj: arksinus, arkosinus, arktangens, arkkotangens). Razmotrimo funkcije \arcsin x i \mathrm(arctg)\,x, pošto su druge dvije izražene u njima pomoću formula:

$\arccos x = \frac(π)(2) − \arcsin x,$ $\mathrm(arcctg)\,x = \frac(π)(2) − \mathrm(arctg)\,x.$

Jednakost $y = \arcsin x$ po definiciji znači takav ugao $y,$ izražen u radijanskim mjerama i uključen u raspon od $−\frac(π)(2)$ do $\frac(π)(2) ,$ sinus koji je jednak $x,$ tj. $\sin y = x.$ Funkcija $\arcsin x$ je inverzna funkcija funkcije $\sin x,$ razmatrane na intervalu $\left[−\ frac(π)(2),+\frac(π)(2)\right],$ pri čemu se ova funkcija monotono povećava i poprima sve vrijednosti od $−1$ do $+1.$ Očigledno, argument $y$ funkcije $\arcsin x$ može uzimati vrijednosti samo iz segmenta $\left[−1,+1\right].$ Dakle, funkcija $y=\arcsin x$ je definirana na segmentu $\left[−1,+1\right],$ monotono raste, a njegove vrijednosti ispunjavaju segment $\left[−\frac(π)(2),+\frac(π)(2)\ desno].$ Grafikon funkcije je prikazan na sl. $2.$

Pod uslovom $−1 ≤ a ≤ 1$, sva rješenja jednačine $\sin x = a$ predstavljamo kao $x=(−1)^n \arcsin a + πn,$ $n=0,±1 ,± 2, … .$ Na primjer, ako

$\sin x = \frac(\sqrt(2))(2)$ tada je $x = (−1)^n \frac(π)(4)+πn,$ $n = 0, ±1, ±2 , … .$

Relacija $y=\mathrm(arcctg)\,x$ je definirana za sve vrijednosti $x$ i po definiciji znači da je ugao $y,$ izražen u radijanskoj mjeri unutar

$−\frac(π)(2)

a tangenta ovog ugla je x, tj. $\mathrm(tg)\,y = x.$ Funkcija $\mathrm(arctg)\,x$ je definirana na cijeloj realnoj pravoj, inverzna je funkcija funkcije $\mathrm(tg)\,x$, koji se razmatra samo na intervalu

$−\frac(π)(2)

Funkcija $y = \mathrm(arctg)\,x$ je monotono rastuća, njen graf je dat na sl. $3.$

Sva rješenja jednadžbe $\mathrm(tg)\,x = a$ mogu se napisati kao $x=\mathrm(arctg)\,a+πn,$ $n=0,±1,±2,… .$

Imajte na umu da se inverzne trigonometrijske funkcije široko koriste u matematičkoj analizi. Na primjer, jedna od prvih funkcija za koju je dobijena beskonačna reprezentacija potencijskog niza bila je funkcija $\mathrm(arctg)\,x.$ blizu

Zadaci koji se odnose na inverzne trigonometrijske funkcije često se nude na školskim završnim ispitima i na prijemnim ispitima na nekim univerzitetima. Detaljno proučavanje ove teme može se postići samo u vannastavnoj nastavi ili u izbornim predmetima. Predloženi kurs je osmišljen tako da što potpunije razvije sposobnosti svakog polaznika, da unapredi njegovu matematičku obuku.

Kurs je predviđen za 10 sati:

1. Funkcije arcsin x, arccos x, arctg x, arcctg x (4 sata).

2. Operacije nad inverznim trigonometrijskim funkcijama (4 sata).

3. Inverzne trigonometrijske operacije na trigonometrijskim funkcijama (2 sata).

Lekcija 1 (2 sata) Tema: Funkcije y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.

Svrha: potpuna pokrivenost ovog pitanja.

1. Funkcija y \u003d arcsin x.

a) Za funkciju y = sin x na segmentu postoji inverzna (jednoznačna) funkcija, koju smo dogovorili nazvati arcsinusom i označiti na sljedeći način: y = arcsin x. Grafikon inverzne funkcije je simetričan sa grafikom glavne funkcije u odnosu na simetralu I - III koordinatnih uglova.

Svojstva funkcije y = arcsin x .

1) Obim definicije: segment [-1; jedan];

2) Područje promjene: rez;

3) Funkcija y = arcsin x neparan: arcsin (-x) = - arcsin x;

4) Funkcija y = arcsin x monotono raste;

5) Grafikon prelazi ose Ox, Oy na početku.

Primjer 1. Pronađite a = arcsin . Ovaj primjer se može detaljno formulirati na sljedeći način: pronađite takav argument a , koji leži u rasponu od do , čiji je sinus jednak .

Odluka. Postoji bezbroj argumenata čiji je sinus, na primjer: itd. Ali nas zanima samo argument koji je na intervalu. Ovaj argument će biti . Dakle, .

Primjer 2. Pronađite .Odluka. Argumentirajući na isti način kao u primjeru 1, dobijamo .

b) oralne vježbe. Pronađite: arcsin 1, arcsin (-1), arcsin , arcsin (), arcsin , arcsin (), arcsin , arcsin (), arcsin 0 Primer odgovora: , jer . Da li izrazi imaju smisla: ; arcsin 1.5; ?

c) Rasporedite u rastućem redoslijedu: arcsin, arcsin (-0,3), arcsin 0,9.

II. Funkcije y = arccos x, y = arctg x, y = arcctg x (slično).

Lekcija 2 (2 sata) Tema: Inverzne trigonometrijske funkcije, njihovi grafovi.

Svrha: u ovoj lekciji potrebno je razraditi vještine određivanja vrijednosti trigonometrijskih funkcija, crtanja inverznih trigonometrijskih funkcija pomoću D (y), E (y) i potrebnih transformacija.

U ovoj lekciji izvodite vježbe koje uključuju pronalaženje domene definicije, opsega funkcija tipa: y = arcsin , y = arccos (x-2), y = arctg (tg x), y = arccos .

Potrebno je izgraditi grafove funkcija: a) y = arcsin 2x; b) y = 2 arcsin 2x; c) y \u003d arcsin;

d) y \u003d arcsin; e) y = arcsin; f) y = arcsin; g) y = | arcsin | .

Primjer. Nacrtajmo y = arccos

U svoj domaći zadatak možete uključiti sljedeće vježbe: izgraditi grafove funkcija: y = arccos , y = 2 arcctg x, y = arccos | x | .

Grafovi inverznih funkcija

Lekcija #3 (2 sata) Tema:

Operacije nad inverznim trigonometrijskim funkcijama.

Svrha: proširiti matematičko znanje (ovo je važno za kandidate za specijalnosti sa povećanim zahtjevima za matematičku pripremu) uvođenjem osnovnih odnosa za inverzne trigonometrijske funkcije.

Materijal za lekciju.

Neke jednostavne trigonometrijske operacije nad inverznim trigonometrijskim funkcijama: sin (arcsin x) \u003d x, i xi? jedan; cos (arscos x) = x, i xi? jedan; tg (arctg x)= x , x I R; ctg (arcctg x) = x , x I R.

Vježbe.

a) tg (1,5 + arctg 5) = - ctg (arctg 5) = .

ctg (arctgx) = ; tg (arctgx) = .

b) cos (+ arcsin 0,6) = - cos (arcsin 0,6). Neka je arcsin 0,6 \u003d a, sin a \u003d 0,6;

cos(arcsin x) = ; sin (arccos x) = .

Napomena: uzimamo znak “+” ispred korijena jer a = arcsin x zadovoljava .

c) sin (1,5 + arcsin) Odgovor:;

d) ctg ( + arctg 3) Odgovor: ;

e) tg (- arcctg 4) Odgovor: .

f) cos (0,5 + arccos) . Odgovor: .

Izračunati:

a) sin (2 arktan 5) .

Neka je arctg 5 = a, zatim sin 2 a = ili sin(2 arktan 5) = ;

b) cos (+ 2 arcsin 0,8) Odgovor: 0,28.

c) arctg + arctg.

Neka je a = arctg, b = arctg,

tada tan(a + b) = .

d) sin (arcsin + arcsin).

e) Dokazati da je za sve x I [-1; 1] true arcsin x + arccos x = .

dokaz:

arcsin x = - arccos x

sin (arcsin x) = sin (- arccos x)

x = cos (arccos x)

Za samostalno rješenje: sin (arccos ), cos (arcsin ) , cos (arcsin ()), sin (arctg (- 3)), tg (arccos ) , ctg (arccos ).

Za kućno rešenje: 1) sin (arcsin 0,6 + arctg 0); 2) arcsin + arcsin; 3) ctg ( - arccos 0,6); 4) cos (2 arcctg 5) ; 5) sin (1,5 - arcsin 0,8); 6) arctg 0,5 - arctg 3.

Lekcija br. 4 (2 sata) Tema: Operacije nad inverznim trigonometrijskim funkcijama.

Svrha: u ovoj lekciji pokazati upotrebu omjera u transformaciji složenijih izraza.

Materijal za lekciju.

USMENI:

a) sin (arccos 0,6), cos (arcsin 0,8);

b) tg (arctg 5), ctg (arctg 5);

c) sin (arctg -3), cos (arctg ());

d) tg (arccos), ctg (arccos()).

NAPISANO:

1) cos (arcsin + arcsin + arcsin).

2) cos (arctg 5 - arccos 0,8) = cos (arctg 5) cos (arctg 0,8) + sin (arctg 5) sin (arccos 0,8) =

3) tg (- arcsin 0,6) = - tg (arcsin 0,6) =

4)

Samostalni rad pomoći će u određivanju nivoa asimilacije materijala

1) tg ( arctg 2 - arctg ) 2) cos( - arctg2) 3) arcsin + arccos	1) cos (arcsin + arcsin) 2) sin (1.5 - arctg 3) 3) arcctg3 - arctg 2

Za domaću zadaću možete ponuditi:

1) ctg (arctg + arctg + arctg); 2) sin 2 (arctg 2 - arcctg ()); 3) sin (2 arctg + tg ( arcsin )); 4) sin (2 arktan); 5) tg ( (arcsin))

Lekcija br. 5 (2h) Tema: Inverzne trigonometrijske operacije nad trigonometrijskim funkcijama.

Svrha: formirati razumijevanje učenika o inverznim trigonometrijskim operacijama nad trigonometrijskim funkcijama, fokusirati se na povećanje smisla teorije koja se proučava.

Prilikom proučavanja ove teme, pretpostavlja se da je količina teorijskog materijala za pamćenje ograničena.

Materijal za lekciju:

Možete početi učiti novi materijal tako što ćete ispitati funkciju y = arcsin (sin x) i nacrtati je.

3. Svaki x I R je povezan sa y I , tj.<= y <= такое, что sin y = sin x.

4. Funkcija je neparna: sin (-x) \u003d - sin x; arcsin(sin(-x)) = - arcsin(sin x).

6. Grafikon y = arcsin (sin x) na:

a) 0<= x <= имеем y = arcsin(sin x) = x, ибо sin y = sin x и <= y <= .

b)<= x <= получим y = arcsin (sin x) = arcsin ( - x) = - x, ибо

sin y = sin ( - x) = sinx, 0<= - x <= .

dakle,

Izgradivši y = arcsin (sin x) na , nastavljamo simetrično oko ishodišta na [- ; 0], uzimajući u obzir neparnost ove funkcije. Koristeći periodičnost, nastavljamo do cijele numeričke ose.

Zatim zapišite neke omjere: arcsin (sin a) = a if<= a <= ; arccos (cos a ) = a ako je 0<= a <= ; arctg (tg a) = a if< a < ; arcctg (ctg a) = a , если 0 < a < .

I uradite sljedeće vježbe: a) arccos (sin 2) Odgovor: 2 - ; b) arcsin (cos 0,6) Odgovor: - 0,1; c) arctg (tg 2) Odgovor: 2 -;

d) arcctg (tg 0,6) Odgovor: 0,9; e) arccos (cos ( - 2)) Odgovor: 2 -; f) arcsin (sin (-0,6)). Odgovor: - 0,6; g) arctg (tg 2) = arctg (tg (2 - )). Odgovor: 2 - ; h) arcctg (tg 0,6). Odgovor: - 0,6; - arktanks; e) arccos + arccos

Šta je arcsin, arkosinus? Šta je arc tangenta, arc tangenta?

Pažnja!
Postoje dodatni
materijali u Posebni odjeljak 555.
Za one koji snažno "ne baš..."
I za one koji "jako...")

Za koncepte arksinus, arkosinus, arktangens, arkotangens studentska populacija je oprezna. On ne razumije ove pojmove i stoga ne vjeruje ovoj slavnoj porodici.) Ali uzalud. Ovo su vrlo jednostavni koncepti. Koje, inače, znatno olakšavaju život upućenoj osobi pri odlučivanju trigonometrijske jednačine!

Zbunjeni ste zbog jednostavnosti? Uzalud.) Upravo ovdje i sada ćete se u to uvjeriti.

Naravno, za razumijevanje, bilo bi lijepo znati šta je sinus, kosinus, tangent i kotangens. da ih tablične vrijednosti za neke uglove... Barem u najopštijem smislu. Onda ni ovdje neće biti problema.

Dakle, iznenađeni smo, ali zapamtite: arksinus, arkosinus, arktangens i arktangens su samo neki uglovi. Ni više, ni manje. Postoji ugao, recimo 30°. I postoji ugao arcsin0.4. Or arctg(-1.3). Ima raznih uglova.) Možete jednostavno napisati uglove na različite načine. Možete napisati ugao u terminima stepeni ili radijani. Ili možete - kroz njegov sinus, kosinus, tangens i kotangens...

Šta izraz znači

arcsin 0.4?

Ovo je ugao čiji je sinus 0,4! Da da. Ovo je značenje arcsinusa. Konkretno ponavljam: arcsin 0,4 je ugao čiji je sinus 0,4.

I to je to.

Da bih ovu jednostavnu misao dugo zadržao u svojoj glavi, čak ću dati i raščlambu ovog strašnog pojma - arcsin:

arc grijeh 0,4
injekcija, čiji sinus jednako 0,4

Kako se piše, tako se i čuje.) Skoro. Prefiks arc znači arc(reč arh znate?), jer stari ljudi su koristili lukove umjesto uglova, ali to ne mijenja suštinu stvari. Zapamtite ovo elementarno dekodiranje matematičkog pojma! Štoviše, za arc kosinus, arc tangent i arc tangent, dekodiranje se razlikuje samo u nazivu funkcije.

Šta je arccos 0.8?
Ovo je ugao čiji je kosinus 0,8.

Šta je arktan(-1,3)?
Ovo je ugao čiji je tangent -1,3.

Šta je arcctg 12?
Ovo je ugao čiji je kotangens 12.

Takvo elementarno dekodiranje omogućava, inače, izbjegavanje epskih grešaka.) Na primjer, izraz arccos1,8 izgleda sasvim solidno. Počnimo s dekodiranjem: arccos1,8 je ugao čiji je kosinus jednak 1,8... Hop-hop!? 1.8!? Kosinus ne može biti veći od jedan!

U redu. Izraz arccos1,8 nema smisla. A pisanje takvog izraza u nekom odgovoru će jako zabaviti verifikatora.)

Elementarno, kao što vidite.) Svaki ugao ima svoj lični sinus i kosinus. I skoro svako ima svoju tangentu i kotangens. Stoga, poznavajući trigonometrijsku funkciju, možete zapisati sam ugao. Za to su namijenjeni arksinus, arkosinus, arktangens i arkkotangens. Dalje, celu ovu porodicu ću nazvati umanjenicom - lukovi. da manje kucate.)

Pažnja! Elementarni verbalni i svjesni dešifriranje lukova omogućava vam da mirno i samouvjereno rješavate razne zadatke. I unutra neobično zadatke samo ona spašava.

Da li je moguće preći sa lukova na obične stepene ili radijane?- Čujem oprezno pitanje.)

Zašto ne!? Lako. Možeš ići tamo i nazad. Štaviše, ponekad je to neophodno učiniti. Lukovi su jednostavna stvar, ali bez njih je nekako mirnije, zar ne?)

Na primjer: šta je arcsin 0,5?

Pogledajmo dešifrovanje: arcsin 0,5 je ugao čiji je sinus 0,5. Sada okrenite glavu (ili Google)) i zapamtite koji ugao ima sinus od 0,5? Sinus je 0,5 y ugao od 30 stepeni. To je sve o tome: arcsin 0,5 je ugao od 30°. Možete sa sigurnošću napisati:

arcsin 0,5 = 30°

Ili, preciznije, u radijanima:

To je to, možete zaboraviti na arcsin i raditi s uobičajenim stepenima ili radijanima.

Ako ste shvatili šta je arksinus, arkosinus... Šta je arktangens, arkkotangens... Tada se lako možete nositi s, na primjer, takvim čudovištem.)

Neupućena osoba će ustuknuti od užasa, da...) I upućena zapamtite dešifrovanje: arksinus je ugao čiji je sinus ... Pa, i tako dalje. Ako i upućena osoba zna tabela sinusa... tabela kosinusa. Tabela tangenti i kotangensa, onda nema nikakvih problema!

Dovoljno je uzeti u obzir da:

Ja ću dešifrovati, tj. prevedi formulu u riječi: ugao čija je tangenta 1 (arctg1) je ugao od 45°. Ili, što je isto, Pi/4. Slično:

i to je sve... Sve lukove zamjenjujemo vrijednostima u radijanima, sve se smanjuje, ostaje da izračunamo koliko će biti 1 + 1. Biće 2.) Što je tačan odgovor.

Ovo je način na koji možete (i trebate) prijeći od arksinusa, arkkosinusa, arktangensa i arktangensa do običnih stupnjeva i radijana. Ovo uvelike pojednostavljuje zastrašujuće primjere!

Često su, u takvim primjerima, unutar lukova negativan vrijednosti. Kao, arctg(-1.3), ili, na primjer, arccos(-0.8)... To nije problem. Evo nekoliko jednostavnih formula za prelazak iz negativnog u pozitivno:

Trebate, recimo, da odredite vrijednost izraza:

Ovo možete riješiti pomoću trigonometrijskog kruga, ali ga ne želite crtati. Pa, ok. Idem iz negativan vrijednosti unutar arc kosinusa do pozitivno prema drugoj formuli:

Već unutar arkosinusa na desnoj strani pozitivno značenje. Šta

samo moraš znati. Ostaje zamijeniti radijane umjesto arc kosinusa i izračunati odgovor:

To je sve.

Ograničenja za arksinus, arkosinus, arktangens, arkkotangens.

Postoji li problem sa primjerima 7 - 9? Pa, da, postoji neki trik.)

Svi ovi primjerci, od 1. do 9., pažljivo su razvrstani po policama Član 555.Šta, kako i zašto. Sa svim tajnim zamkama i trikovima. Plus načini za dramatično pojednostavljenje rješenja. Inače, ovaj odjeljak sadrži puno korisnih informacija i praktičnih savjeta o trigonometriji općenito. I ne samo u trigonometriji. Pomaže puno.

Ako vam se sviđa ovaj sajt...

Inače, imam još par zanimljivih stranica za vas.)

Možete vježbati rješavanje primjera i saznati svoj nivo. Testiranje sa trenutnom verifikacijom. Učenje - sa interesovanjem!)

možete se upoznati sa funkcijama i izvedenicama.

Inverzne trigonometrijske funkcije(kružne funkcije, lučne funkcije) - matematičke funkcije koje su inverzne trigonometrijskim funkcijama.

One obično uključuju 6 ​​funkcija:

• arcsine(simbol: arcsin x; arcsin x je ugao grijehšto je jednako x),
• arccosine(simbol: arccos x; arccos x je ugao kojem je kosinus jednak x itd),
• arc tangent(simbol: arctg x ili arctan x),
• arc tangent(simbol: arcctg x ili arccot ​​x ili arccotan x),
• arcsecant(simbol: arcsec x),
• arccosecan(simbol: arccosec x ili arccsc x).

Arcsine (y = arcsin x) je inverzna funkcija prema grijeh (x = sin . Drugim riječima, vraća ugao po njegovoj vrijednosti grijeh.

Arc kosinus (y = arccos x) je inverzna funkcija prema cos (x = cos y cos.

Arktangent (y = arktan x) je inverzna funkcija prema tg (x = tgy), koji ima domen definicije i skup vrijednosti . Drugim riječima, vraća ugao po njegovoj vrijednosti tg.

Arc tangent (y = arcctg x) je inverzna funkcija prema ctg (x = ctg y), koji ima domenu definicije i skup vrijednosti. Drugim riječima, vraća ugao po njegovoj vrijednosti ctg.

arcsec- arcsecant, vraća ugao po vrijednosti njegove sekante.

arccosec- arccosecans, vraća ugao po vrijednosti njegovog kosekansa.

Kada inverzna trigonometrijska funkcija nije definirana u navedenoj tački, tada se njena vrijednost neće pojaviti u rezultirajućoj tablici. Funkcije arcsec i arccosec nisu definisani na segmentu (-1,1), ali arc sin i arccos definisani su samo na intervalu [-1,1].

Naziv inverzne trigonometrijske funkcije formira se od naziva odgovarajuće trigonometrijske funkcije dodavanjem prefiksa "ark-" (od lat. arc nas- luk). To je zbog činjenice da je geometrijski vrijednost inverzne trigonometrijske funkcije povezana s dužinom luka jedinične kružnice (ili kuta koji savija ovaj luk), koji odgovara jednom ili drugom segmentu.

Ponekad se u stranoj literaturi, kao iu naučnim/inženjerskim kalkulatorima, koriste oznake poput sin −1, cos -1 za arcsin, arkosinus i slično - ovo se smatra nepotpuno tačnim, jer vjerovatno zabuna sa podizanjem funkcije na stepen −1 (« −1 » (minus prvi stepen) definira funkciju x=f-1(y), inverzna funkcija y=f(x)).

Osnovne relacije inverznih trigonometrijskih funkcija.

Ovdje je važno obratiti pažnju na intervale za koje vrijede formule.

Formule koje se odnose na inverzne trigonometrijske funkcije.

Označite bilo koju od vrijednosti inverznih trigonometrijskih funkcija kroz Arcsin x, Arccos x, Arctan x, Arccot ​​x i zadrži notaciju: arcsin x, arcos x, arctan x, arccot ​​x za njihove glavne vrijednosti, onda se odnos između njih izražava takvim odnosima.