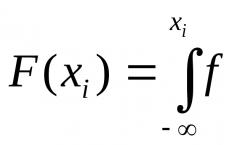Méthode de la fonction inverse

Soit qu'il soit demandé de jouer une variable aléatoire continue X, c'est-à-dire obtenir la séquence de ses valeurs possibles X je (je= 1,2, ...), connaissant la fonction de distribution F(X).

Théorème. Si r je ,-nombre aléatoire, puis valeur possibleX je variable aléatoire continue X jouée avec une fonction de distribution donnéeF(X)correspondantr je , est la racine de l'équation

F(X je)= r je . (»)

Preuve. Laisser un nombre aléatoire être choisi r je (0≤r je <1). Так как в интервале всех возможных зна­чений X fonction de répartition F(X) croît de manière monotone de 0 à 1, alors dans cet intervalle il existe, et une seule, une telle valeur de l'argument X je , où la fonction de distribution prend la valeur r je. En d'autres termes, l'équation (*) a une solution unique

X je = F - 1 (r je),

Où F - 1 - fonction inverse y=F(X).

Prouvons maintenant que la racine X je l'équation (*) est une valeur possible d'une telle variable aléatoire continue (nous la noterons provisoirement par ξ , puis assurez-vous que ξ=X). Pour cela, nous montrons que la probabilité de toucher ξ dans un intervalle, par exemple ( Avec,d), appartenant à l'intervalle de toutes les valeurs possibles X, est égal à l'incrément de la fonction de distribution F(X) sur cet intervalle :

R(Avec< ξ < d)= F(d)- F(Avec).

En effet, depuis F(X)- fonction monotone croissante dans l'intervalle de toutes les valeurs possibles X, alors dans cet intervalle, les grandes valeurs de l'argument correspondent aux grandes valeurs de la fonction, et inversement. Par conséquent, si Avec <X je < d, Ce F(c)< r je < F(d), et vice versa [en tenant compte du fait qu'en raison de (*) F(X je)=r je ].

De ces inégalités, il résulte que si la variable aléatoire ξ enfermé dans l'intervalle

Avec< ξ < d, ξ (**)

alors la variable aléatoire R enfermé dans l'intervalle

F(Avec)< R< F(d), (***)

et retour. Ainsi, les inégalités (**) et (***) sont équivalentes, donc équiprobables :

R(Avec< ξ< d)=P[F(Avec)< R< F(d)]. (****)

Puisque la valeur R distribué uniformément dans l'intervalle (0,1), alors la probabilité de toucher Rà un intervalle appartenant à l'intervalle (0,1) est égal à sa longueur (voir Chap. XI, § 6, remarque). En particulier,

R[F(Avec)< R< F(d) ] = F(d) - F(Avec).

Par conséquent, la relation (****) peut être écrite comme

R(Avec< ξ< d)= F(d) - F(Avec).

Donc la probabilité de toucher ξ dans l'intervalle ( Avec,d) est égal à l'incrément de la fonction de distribution F(X) sur cet intervalle, ce qui signifie que ξ=X. Autrement dit, les chiffres X je, défini par la formule (*), il existe des valeurs possibles de la quantité X s fonction de distribution donnée F(X), Q.E.D.

Règle 1X je , variable aléatoire continue X, connaissant sa fonction de distribution F(X), vous devez choisir un nombre au hasard r jeégaliser ses fonctions de distribution et résoudre pour X je , équation résultante

F(X je)= r je .

Remarque 1. Si cette équation ne peut pas être résolue explicitement, alors on a recours à des méthodes graphiques ou numériques.

Exemple I Jouer 3 valeurs possibles d'une variable aléatoire continue X, répartis uniformément dans l'intervalle (2, 10).

Solution. Écrivons la fonction de distribution de la quantité X, distribué uniformément dans l'intervalle ( UN,b) (voir Ch. XI, § 3, exemple) :

F(X)= (Ha)/ (b-UN).

Par état, un = 2, b=10, donc,

F(X)= (X- 2)/ 8.

En utilisant la règle de cette section, nous écrivons une équation pour trouver les valeurs possibles X je , pour lequel on assimile la fonction de distribution à un nombre aléatoire :

(X je -2 )/8= r je .

D'ici X je =8 r je + 2.

Choisissons 3 nombres aléatoires, par exemple, r je =0,11, r je =0,17, r je=0,66. Remplacez ces nombres dans l'équation, résolue par rapport à X je , en conséquence, nous obtenons les valeurs possibles correspondantes X: X 1 \u003d 8 0,11 + 2 \u003d\u003d 2,88; X 2 =1.36; X 3 = 7,28.

Exemple 2 Variable aléatoire continue X distribué selon la loi exponentielle donnée par la fonction de distribution (le paramètre λ > 0 est connu)

F(X)= 1 - e - λ X (x>0).

Il faut trouver une formule explicite pour jouer les valeurs possibles X.

Solution. En utilisant la règle de ce paragraphe, on écrit l'équation

1 - e - λ X je

Résolvons cette équation pour X je :

e - λ X je = 1 - r je, ou - λ X je = dans(1 - r je).

X je =1p(1– r je)/λ .

Nombre aléatoire r je inclus dans l'intervalle (0,1); d'où le chiffre 1 - r je, également aléatoire et appartient à l'intervalle (0,1). Autrement dit, les quantités R et 1- R répartis équitablement. Par conséquent, pour trouver X je Vous pouvez utiliser une formule plus simple :

X je =- dans r je /λ.

Remarque 2. On sait que (voir Ch. XI, §3)

En particulier,

Il s'ensuit que si la densité de probabilité est connue F(X), puis jouer X au lieu des équations F(X je)=r je décider X je l'équation

Règle 2 Pour trouver une valeur possible X je (variable aléatoire continue X, connaissant sa densité de probabilité F(X) choisissez un nombre au hasard r je et décider de X je , l'équation

ou équation

Où UN- la plus petite valeur finale possible X.

Exemple 3Étant donné la densité de probabilité d'une variable aléatoire continue XF(X)=λ (1-λx/2) dans l'intervalle (0 ; 2/λ) ; en dehors de cet intervalle F(X)= 0. Il faut trouver une formule explicite pour jouer les valeurs possibles X.

Solution. On écrit conformément à la règle 2 l'équation

Après avoir intégré et résolu l'équation quadratique résultante pour X je, on obtient enfin

TRAVAIL DE LABORATOIRE MM-03

JOUER DES ROV DISCRETS ET CONTINUS

Objet du travail : étude et implémentation logicielle de méthodes de lecture de RV discrètes et continues

QUESTIONS À ÉTUDIER À PARTIR DU RÉSUMÉ DU COURS :

1. Variables aléatoires discrètes et leurs caractéristiques.

2. Jouer un groupe complet d'événements aléatoires.

3. Lecture d'une variable aléatoire continue par la méthode de la fonction inverse.

4. Choix d'une direction aléatoire dans l'espace.

5. Distribution normale standard et son recalcul pour des paramètres donnés.

6. La méthode des coordonnées polaires pour jouer la distribution normale.

TÂCHE 1. Formulez (par écrit) une règle pour jouer les valeurs d'un RV discret, dont la loi de distribution est donnée sous forme de tableau. Composez une fonction de sous-programme pour lire les valeurs de CV en utilisant le BSV reçu du sous-programme RNG. Jouez 50 valeurs CB et affichez-les à l'écran.

Où N est le numéro de variante.

TÂCHE 2. La fonction de densité de distribution f(x) d'une variable aléatoire continue X est donnée.

Dans le rapport, notez les formules et le calcul des valeurs suivantes :

A) constante de normalisation ;

B) fonction de distribution F(x);

C) espérance mathématique M(X);

D) dispersion D(X);

E) une formule pour jouer les valeurs de CB en utilisant la méthode de la fonction inverse.

Composez une sous-routine de fonction pour jouer le CV donné et obtenez 1000 valeurs de ce CV.

Construire un histogramme de la distribution des nombres obtenus sur 20 segments.

TÂCHE 3.Écrivez une procédure qui vous permet de jouer les paramètres d'une direction aléatoire dans l'espace. Jouez 100 directions aléatoires dans l'espace.

Utilisez le générateur de nombres pseudo-aléatoires intégré.

Le rapport écrit sur les travaux de laboratoire doit contenir :

1) Nom et objet du travail, groupe, nom et numéro de l'option de l'étudiant;

2) Pour chaque tâche : -condition, -formules et transformations mathématiques nécessaires, -nom du fichier programme qui implémente l'algorithme utilisé, -résultats des calculs.

Les fichiers de programme débogués sont remis avec le rapport écrit.

APPLICATION

Variantes de la densité de distribution du SW continu

Var-t	Densité de distribution SW	Var-t	Densité de distribution SW

L'essence de la méthode de Monte Carlo est la suivante : vous devez trouver la valeur UN une valeur à l'étude. A cet effet, on choisit une telle variable aléatoire X dont l'espérance mathématique est égale à a : M(X) = a.

En pratique, ils font ceci : ils calculent (jouent) n valeurs possibles x i d'une variable aléatoire X, trouver leur moyenne arithmétique

Et ils prennent comme estimation (valeur approximative) a * du nombre souhaité a. Ainsi, pour appliquer la méthode de Monte Carlo, il est nécessaire de pouvoir jouer une variable aléatoire.

Soit qu'il soit demandé de jouer une variable aléatoire discrète X, c'est-à-dire calculer la suite de ses valeurs possibles x i (i=1,2, …), connaissant la loi de distribution X. Introduisons la notation : R est une variable aléatoire continue distribuée uniformément dans l'intervalle (0,1) ; r i (j=1,2,…) – nombres aléatoires (valeurs possibles de R).

Règle: Pour jouer une variable aléatoire discrète X donnée par la loi de distribution

X x 1 x 2 ... x n

P p 1 p 2 … p n

1. Décomposez l'intervalle (0,1) de l'axe ou en n intervalles partiels :

Δ 1 = (0 ; p 1), Δ 2 = (p 1 ; p 1+ p 2), ..., Δ n = (p 1 + p 2 + ... + p n -1 ; 1).

2. Choisissez un nombre aléatoire r j . Si r j tombe dans l'intervalle partiel Δ i , alors la valeur jouée prend la valeur possible de x i . .

Jouer un groupe complet d'événements

Il est nécessaire de jouer des tests, dans chacun desquels se produit l'un des événements du groupe complet, dont les probabilités sont connues. Jouer un groupe complet d'événements revient à jouer une variable aléatoire discrète.

Règle: Pour jouer des tests, dans chacun desquels survient un des événements A 1, A 2, ..., A n du groupe complet, dont les probabilités p 1, p 2, ..., p n sont connues, il suffit de jouer une valeur discrète X avec la loi de distribution suivante :

P p 1 p 2 … p n

Si dans le test la valeur X a pris la valeur possible x i =i, alors l'événement A i s'est produit.

Lecture d'une variable aléatoire continue

On connaît la fonction de distribution F d'une variable aléatoire continue X. Il faut jouer X, c'est-à-dire calculer la suite des valeurs possibles x i (i=1,2, …).

A. Méthode des fonctions inverses. Règle 1 x i d'une variable aléatoire continue X, connaissant sa fonction de distribution F, vous devez choisir un nombre aléatoire r i , égaliser sa fonction de distribution et résoudre pour x i l'équation résultante F(х i) = r i .

Si la densité de probabilité f(x) est connue, alors la règle 2 est utilisée.

Règle 2 Pour jouer le sens possible x i d'une variable aléatoire continue X, connaissant sa densité de probabilité f, vous devez choisir un nombre aléatoire r i et résoudre l'équation pour x i

ou équation

où a est la plus petite valeur finie possible de X.

B. Méthode de superposition. Règle 3 Pour jouer la valeur possible d'une variable aléatoire X, dont la fonction de distribution

F(x) = C 1 F 1 (x)+C 2 F 2 (x)+…+C n F n (x),

où F k (x) – fonctions de répartition (k=1, 2, …, n), С k >0, С i +С 2 +…+С n =1, il faut choisir deux nombres aléatoires indépendants r 1 et r 2 et utiliser le nombre aléatoire r 1 pour jouer la valeur possible de la variable aléatoire discrète auxiliaire Z (selon la règle 1) :

p C 1 C 2 … C n

S'il s'avère que Z=k, alors l'équation F k (x) = r 2 est résolue pour x.

Remarque 1. Si la densité de probabilité d'une variable aléatoire continue X est donnée sous la forme

f(x)=C 1 f 1 (x)+C 2 f 2 (x)+…+C n f n (x),

où f k sont les densités de probabilité, les coefficients C k sont positifs, leur somme est égale à un, et s'il s'avère que Z=k, alors ils résolvent (selon la règle 2) par rapport à x i par rapport à ou l'équation

Jeu approximatif d'une variable aléatoire normale

Règle. Pour estimer la valeur possible x i d'une variable aléatoire normale X de paramètres a=0 et σ=1, ajouter 12 nombres aléatoires indépendants et soustraire 6 de la somme résultante :

Commentaire. Si vous voulez jouer approximativement une variable aléatoire normale Z avec une espérance mathématique UN et l'écart-type σ, puis, après avoir joué la valeur possible de x i selon la règle ci-dessus, ils trouvent la valeur possible souhaitée par la formule : z i =σx i +a.

Définition 24.1.nombres aléatoires nommer les valeurs possibles r variable aléatoire continue R, distribué uniformément dans l'intervalle (0; 1).

1. Jouer une variable aléatoire discrète.

Soit qu'il soit demandé de jouer une variable aléatoire discrète X, c'est-à-dire obtenir une séquence de ses valeurs possibles, connaissant la loi de distribution X:

x x 1 X 2 … x n

pp 1 R 2 … r p .

Considérons une variable aléatoire uniformément distribuée dans (0, 1) R et diviser l'intervalle (0, 1) par des points de coordonnées R 1, R 1 + R 2 , …, R 1 + R 2 +… +r p-1 sur P intervalles partiels dont les longueurs sont égales aux probabilités de mêmes indices.

Théorème 24.1. Si chaque nombre aléatoire qui tombe dans l'intervalle se voit attribuer une valeur possible , alors la valeur jouée aura une loi de distribution donnée :

x x 1 X 2 … x n

pp 1 R 2 … r p .

Preuve.

Les valeurs possibles de la variable aléatoire obtenue coïncident avec l'ensemble X 1 , X 2 ,… x n, puisque le nombre d'intervalles est P, et lorsqu'il est touché r j dans l'intervalle, une variable aléatoire ne peut prendre qu'une des valeurs X 1 , X 2 ,… x n.

Parce que R est uniformément distribuée, alors la probabilité qu'il tombe dans chaque intervalle est égale à sa longueur, ce qui implique que chaque valeur correspond à la probabilité pi. Ainsi, la variable aléatoire jouée a une loi de distribution donnée.

Exemple. Jouer 10 valeurs d'une variable aléatoire discrète X, dont la loi de distribution est de la forme : X 2 3 6 8

R 0,1 0,3 0,5 0,1

Solution. Décomposons l'intervalle (0, 1) en intervalles partiels : D 1 - (0 ; 0,1), D 2 - (0,1 ; ​​0,4), D 3 - (0,4 ; 0,9), D 4 - (0,9 ; 1). Écrivons 10 nombres du tableau des nombres aléatoires : 0,09 ; 0,73 ; 0,25 ; 0,33 ; 0,76 ; 0,52 ; 0,01 ; 0,35 ; 0,86 ; 0,34. Les premier et septième nombres se trouvent sur l'intervalle D 1 , donc, dans ces cas, la variable aléatoire jouée a pris la valeur X 1 = 2 ; les troisième, quatrième, huitième et dixième nombres sont tombés dans l'intervalle D 2 , ce qui correspond à X 2 = 3 ; les deuxième, cinquième, sixième et neuvième numéros étaient dans l'intervalle D 3 - tandis que X = X 3 = 6 ; pas un seul nombre n'est tombé dans le dernier intervalle. Ainsi, les valeurs possibles jouées X sont : 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. Jouer des événements opposés.

Qu'il soit exigé de jouer des épreuves, dans chacune desquelles l'événement UN apparaît avec une probabilité connue R. Considérons une variable aléatoire discrète X, qui prend les valeurs 1 (si l'événement UN arrivé) avec une probabilité R et 0 (si UN ne s'est pas produit) avec une probabilité q = 1 – p. Ensuite, nous jouons cette variable aléatoire comme suggéré dans le paragraphe précédent.

Exemple. Jouez à 10 défis, chacun avec un événement UN apparaît avec une probabilité de 0,3.

Solution. Pour une variable aléatoire X avec loi de distribution X 1 0

R 0,3 0,7

on obtient les intervalles D 1 - (0 ; 0,3) et D 2 - (0,3 ; 1). Nous utilisons le même échantillon de nombres aléatoires que dans l'exemple précédent, pour lequel les nombres №№1,3 et 7 tombent dans l'intervalle D 1, et le reste - dans l'intervalle D 2 . On peut donc supposer que l'événement UN s'est produit dans les première, troisième et septième épreuves, mais ne s'est pas produit dans les autres.

3. Jouer un groupe complet d'événements.

Si les événements UN 1 , UN 2 , …, Un p, dont les probabilités sont égales R 1 , R 2 ,… r p, formez un groupe complet, puis pour jouer (c'est-à-dire modéliser la séquence de leurs apparitions dans une série de tests), vous pouvez jouer une variable aléatoire discrète X avec loi de distribution X 1 2 … P, faire cela de la même manière qu'au paragraphe 1. En même temps, nous supposons que

pp 1 R 2 … r p

Si X prend la valeur x je = je, alors dans ce procès un événement s'est produit Un je.

4. Jouer une variable aléatoire continue.

a) Méthode des fonctions inverses.

Soit qu'il soit demandé de jouer une variable aléatoire continue X, c'est-à-dire obtenir la séquence de ses valeurs possibles x je (je = 1, 2, …, n), connaissant la fonction de distribution F(X).

Théorème 24.2. Si r je est un nombre aléatoire, alors la valeur possible x je variable aléatoire continue jouée X avec une fonction de distribution donnée F(X), correspondant r je, est la racine de l'équation

F(x je) = r je. (24.1)

Preuve.

Parce que F(X) augmente de manière monotone dans la plage de 0 à 1, alors il existe une valeur (et unique) de l'argument x je, auquel la fonction de distribution prend la valeur r je. Ainsi, l'équation (24.1) a une solution unique : x je= F -1 (r je), Où F-1 - fonction inverse de F. Montrons que la racine de l'équation (24.1) est une valeur possible de la variable aléatoire considérée X. Supposons d'abord que x je est une valeur possible d'une variable aléatoire x, et nous prouvons que la probabilité que x tombe dans l'intervalle ( c, ré) est égal à F(d) – F(c). En effet, du fait de la monotonie F(X) et cela F(x je) = r je. Alors

Par conséquent, Par conséquent, la probabilité que x tombe dans l'intervalle ( c, ré) est égal à l'incrément de la fonction de distribution F(X) sur cet intervalle, donc x = X.

Jouer 3 valeurs possibles d'une variable aléatoire continue X, répartis uniformément dans l'intervalle (5 ; 8).

F(X) = , c'est-à-dire qu'il est nécessaire pour résoudre l'équation Choisissons 3 nombres aléatoires : 0,23 ; 0,09 et 0,56 et substituez-les dans cette équation. Obtenir les valeurs possibles correspondantes X:

b) Méthode de superposition.

Si la fonction de distribution de la variable aléatoire jouée peut être représentée comme une combinaison linéaire de deux fonctions de distribution :

alors, parce qu'à X®¥ F(X) ® 1.

Nous introduisons une variable aléatoire discrète auxiliaire Z avec loi de distribution

Z 12 . Choisissons 2 nombres aléatoires indépendants r 1 et r 2 et jouer le possible

pc 1 C 2

signification Z par numéro r 1 (voir paragraphe 1). Si Z= 1, alors on cherche la valeur possible souhaitée X de l'équation, et si Z= 2, puis on résout l'équation .

On peut prouver que dans ce cas, la fonction de distribution de la variable aléatoire jouée est égale à la fonction de distribution donnée.

c) Simulation approchée d'une variable aléatoire normale.

Depuis pour R, uniformément distribué dans (0, 1), , alors pour la somme P indépendantes, uniformément distribuées dans l'intervalle (0,1) variables aléatoires . Alors, en vertu du théorème central limite, la variable aléatoire normalisée à P® ¥ aura une distribution proche de la normale, avec des paramètres UN= 0 et s =1. En particulier, une assez bonne approximation est obtenue pour P = 12:

Donc, pour jouer la valeur possible de la variable aléatoire normale normalisée X, vous devez ajouter 12 nombres aléatoires indépendants et soustraire 6 de la somme.

Envoyer votre bon travail dans la base de connaissances est simple. Utilisez le formulaire ci-dessous

Les étudiants, les étudiants diplômés, les jeunes scientifiques qui utilisent la base de connaissances dans leurs études et leur travail vous en seront très reconnaissants.

Hébergé sur http://www.allbest.ru/

ACTIVITÉ 1

Simulation d'événements aléatoires avec une loi de distribution donnée

Lecture d'une variable aléatoire discrète

Supposons qu'il soit nécessaire de jouer une variable aléatoire discrète, c'est-à-dire obtenir la suite de ses valeurs possibles x i (i = 1,2,3,...n), connaissant la loi de distribution X :

Notons R une variable aléatoire continue. La valeur de R est distribuée uniformément dans l'intervalle (0,1). Notons par r j (j = 1,2,...) les valeurs possibles de la variable aléatoire R. Divisons l'intervalle 0< R < 1 на оси 0r точками с координатами на n частичных интервалов.

Alors on obtient :

On voit que la longueur de l'intervalle partiel d'indice i est égale à la probabilité Р de même indice. Longueur

Ainsi, lorsqu'un nombre aléatoire r i tombe dans l'intervalle, la variable aléatoire X prend la valeur x i avec probabilité P i .

Il existe le théorème suivant :

Si chaque nombre aléatoire qui est tombé dans l'intervalle se voit attribuer une valeur possible x i , alors la valeur jouée aura une loi de distribution donnée

Algorithme pour jouer une variable aléatoire discrète donnée par la loi de distribution

1. Il faut décomposer l'intervalle (0,1) de l'axe 0r en n intervalles partiels :

2. Sélectionnez (par exemple, dans une table de nombres aléatoires ou dans un ordinateur) un nombre aléatoire r j .

Si r j tombait dans l'intervalle, alors la variable aléatoire discrète jouée prenait la valeur possible x i .

Lecture d'une variable aléatoire continue

Soit qu'il soit demandé de jouer une variable aléatoire continue X, c'est-à-dire obtenir la suite de ses valeurs possibles x i (i = 1,2,...). Dans ce cas, la fonction de distribution F(X) est connue.

Existe suivant théorème.

Si r i est un nombre aléatoire, alors la valeur possible x i de la variable aléatoire continue jouée X avec une fonction de distribution connue F(X) correspondant à r i est la racine de l'équation

Algorithme pour jouer une variable aléatoire continue :

1. Il faut choisir un nombre aléatoire r i .

2. Mettez en équation le nombre aléatoire sélectionné de la fonction de distribution connue F(X) et obtenez l'équation.

3. Résolvez cette équation pour x i . La valeur résultante x i correspondra simultanément à un nombre aléatoire r i . et étant donné la loi de distribution F(X).

Exemple. Jouez 3 valeurs possibles d'une variable aléatoire continue X distribuée uniformément dans l'intervalle (2 ; 10).

La fonction de distribution de X a la forme suivante :

Par condition, a = 2, b = 10, donc,

Conformément à l'algorithme de jeu d'une variable aléatoire continue, on égalise F(X) au nombre aléatoire choisi r i .. On en déduit :

Remplacez ces nombres dans l'équation (5.3) Nous obtenons les valeurs possibles correspondantes de x:

Problèmes de modélisation d'événements aléatoires avec une loi de distribution donnée

1. Il est nécessaire de jouer 10 valeurs d'une variable aléatoire discrète, c'est-à-dire obtenir une séquence de ses valeurs possibles x i (i=1,2,3,…n), connaissant la loi de distribution X

Choisissons dans la table des nombres aléatoires un nombre aléatoire r j : 0,10 ; 0,12 ; 0,37 ; 0,09 ; 0,65 ; 0,66 ; 0,99 ; 0,19 ; 0,88 ; 0,59 ; 0,78

2. La fréquence de réception des demandes de service est soumise à la loi de distribution exponentielle () , x, le paramètre l est connu (ci-après l = 1/t est l'intensité de réception des demandes)

1 = 0,5 application/heure. Déterminez la séquence de valeurs pour la durée des intervalles entre les réceptions des demandes. Le nombre de réalisations est égal à 5. Nombre r j : 0,10 ; 0,12 ; 0,37 ; 0,09 ; 0,65 ; 0,99 ;

ACTIVITÉ 2

Système de file d'attente

Les systèmes dans lesquels, d'une part, il y a des demandes massives pour l'exécution de tous types de services, et d'autre part, ces demandes sont satisfaites, sont appelés systèmes de file d'attente. Tout QS sert à remplir le flux de candidatures.

Les QS comprennent : une source d'exigences, un flux entrant, une file d'attente, un dispositif de service, un flux sortant de requêtes.

Les SMO sont divisés en :

QS avec pertes (échecs)

CMO avec attente (longueur de file d'attente illimitée)

QS avec une longueur de file d'attente limitée

CMO avec un temps d'attente limité.

Selon le nombre de canaux ou d'appareils de service, les QS sont monocanaux et multicanaux.

Selon la localisation de la source des besoins : ouverte et fermée.

Par le nombre d'éléments de service par besoin : monophasé et multiphasé.

L'une des formes de classification est la classification de D. Kendall - A / B / X / Y / Z

A - détermine la répartition du temps entre les arrivées ;

B - détermine la répartition du temps de service ;

X - détermine le nombre de canaux de service ;

Y - détermine le débit du système (longueur de la file d'attente) ;

Z - détermine l'ordre de service.

Lorsque la capacité du système est infinie et que la commande de service est premier arrivé, premier servi, les parties Y/Z sont omises. Le premier chiffre (A) utilise les symboles suivants :

La distribution M a une loi exponentielle,

G - l'absence de toute hypothèse sur le processus de service, ou il est identifié par le symbole GI, signifiant un processus de service récurrent,

D- déterministe (le temps de service est fixe),

Е n - Erlangien du n-ième ordre,

NM n - hyper-erlangien du n-ième ordre.

Le deuxième chiffre (B) utilise les mêmes caractères.

Le quatrième chiffre (Y) indique la capacité du tampon, c'est-à-dire le nombre maximum de places dans la file d'attente.

Le cinquième chiffre (Z) indique la méthode de choix dans la file d'attente dans un système d'attente : SP-équiprobable, FF-first in-first out, LF-last in-first out, PR-priority.

Pour les tâches :

l - le nombre moyen de candidatures arrivant par unité de temps

µ est le nombre moyen de requêtes servies par unité de temps

Facteur de charge du canal 1, ou pourcentage de temps pendant lequel un canal est occupé.

Caractéristiques principales:

1) P ref - la probabilité de défaillance - la probabilité que le système refuse le service et que l'exigence soit perdue. Cela se produit lorsque le canal ou tous les canaux sont occupés (PSTN).

Pour un QS multicanal R otk = R n , où n est le nombre de canaux de service.

Pour un QS avec une longueur de file d'attente limitée Р otk =Р n + l , où l est la longueur de file d'attente autorisée.

2) Débit relatif q et absolu A du système

q \u003d 1-P otk A \u003d ql

3) Le nombre total d'exigences dans le système

Lsys = n - pour QS avec des échecs, n est le nombre de canaux occupés par le service.

Pour QS avec attente et longueur de file d'attente limitée

L sys \u003d n + L cool

où L exp est le nombre moyen de requêtes en attente de démarrage du service, etc.

Les caractéristiques restantes seront prises en compte lors de la résolution des problèmes.

Systèmes de file d'attente monocanal et multicanal. Systèmes d'échec.

Le modèle monocanal le plus simple avec un flux d'entrée probabiliste et une procédure de service est un modèle caractérisé par une distribution exponentielle à la fois des durées des intervalles entre les arrivées de sinistres et des durées de service. Dans ce cas, la densité de distribution des durées des intervalles entre les arrivées de sinistres a la forme

Densité de distribution de durée de service :

Les flux de requêtes et de services sont les plus simples. Laissez le système fonctionner avec des échecs. Ce type de QS peut être utilisé dans la modélisation des canaux de transmission dans les réseaux locaux. Il est nécessaire de déterminer le débit absolu et relatif du système. Représentons ce système de file d'attente sous la forme d'un graphique (Figure 2), qui a deux états :

S 0 - le canal est libre (en attente) ;

S 1 - le canal est occupé (la demande est en cours de traitement).

Figure 2. Graphique des états d'un QS monocanal avec pannes

Désignons les probabilités d'états : P 0 (t) - la probabilité de l'état « le canal est libre » ; P 1 (t) - la probabilité de l'état "le canal est occupé". Sur la base du graphe d'état étiqueté, nous composons un système d'équations différentielles de Kolmogorov pour les probabilités d'état :

Le système d'équations différentielles linéaires a une solution soumise à la condition de normalisation P 0 (t) + P 1 (t) = 1 . La solution de ce système est dite non stationnaire, car elle dépend directement de t et ressemble à ceci :

P 1 (t) = 1 - P 0 (t) (3.4.3)

Il est facile de voir que pour un QS monocanal avec pannes, la probabilité P 0 (t) n'est rien d'autre que la capacité relative du système q. En effet, P 0 est la probabilité qu'à l'instant t le canal soit libre et que le sinistre arrivé à l'instant t soit servi, et donc, pour un temps t donné, le rapport moyen du nombre de sinistres servis sur le nombre de sinistres entrants est également égal à P 0 (t), soit q = P 0 (t).

Après un long intervalle de temps (at), un mode stationnaire (état stable) est atteint :

Connaissant le débit relatif, il est facile de trouver le débit absolu. Débit absolu (A) - le nombre moyen d'applications que le système de file d'attente peut servir par unité de temps :

La probabilité de refus de service de la requête sera égale à la probabilité de l'état "canal occupé" :

Cette valeur P otk peut être interprétée comme la part moyenne des requêtes non servies parmi celles soumises.

Dans l'écrasante majorité des cas, en pratique, les systèmes de file d'attente sont multicanaux, et, par conséquent, les modèles avec n canaux de desserte (où n > 1) présentent un intérêt certain. Le processus de mise en file d'attente décrit par ce modèle est caractérisé par l'intensité du flux d'entrée l, tandis que pas plus de n clients (requêtes) peuvent être servis en parallèle. Le temps de service moyen pour une demande est de 1/m. Les flux d'entrée et de sortie sont Poisson. Le mode de fonctionnement de l'un ou l'autre canal de service n'affecte pas le mode de fonctionnement des autres canaux de service du système, et la durée de la procédure de service pour chacun des canaux est une variable aléatoire soumise à une loi de distribution exponentielle. Le but ultime de l'utilisation de n canaux de service connectés en parallèle est d'augmenter (par rapport à un système à canal unique) la vitesse de traitement des demandes en servant n clients simultanément. Le graphe d'état d'un système de mise en file d'attente multicanal avec défaillances a la forme illustrée à la figure 4.

Figure 4. Graphe des états d'un QS multicanal avec pannes

S 0 - tous les canaux sont gratuits ;

S 1 - un canal est occupé, les autres sont libres ;

S k - exactement k canaux sont occupés, les autres sont libres ;

S n - tous les n canaux sont occupés, les autres sont libres.

Les équations de Kolmogorov pour les probabilités des états du système P 0 , ... ,P k , ... P n auront la forme suivante :

Les conditions initiales de résolution du système sont les suivantes :

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0 .

La solution stationnaire du système est de la forme :

Les formules de calcul des probabilités P k (3.5.1) sont appelées formules d'Erlang.

Déterminons les caractéristiques probabilistes du fonctionnement d'un QS multicanal avec des pannes en mode stationnaire :

1) probabilité de défaillance :

puisque la requête est rejetée si elle arrive au moment où tous les n canaux sont occupés. La valeur de P otk caractérise la complétude du service du flux entrant ;

2) la probabilité que la demande soit acceptée pour le service (c'est aussi le débit relatif du système q) complète P otk à l'unité :

3) bande passante absolue

4) le nombre moyen de canaux occupés par le service () est le suivant :

La valeur caractérise le degré de chargement du QS.

Tâchesà la leçon 2

1. La branche de communication, qui a un canal, reçoit le flux de messages le plus simple avec une intensité de n = 0,08 messages par seconde. Le temps de transmission est distribué selon la loi exp. Le traitement d'un message se produit avec l'intensité µ=0,1. Les messages arrivant à des moments où le canal de desserte est occupé à transmettre un message précédemment reçu reçoivent un échec de transmission.

Coeff. Charge relative du canal (probabilité que le canal soit occupé)

P

Q est la capacité relative de la branche internodale

Et la bande passante absolue de la branche communication.

2. La branche de communication a un canal et reçoit des messages toutes les 10 secondes. Le temps de service pour un message est de 5 secondes. Le temps de transmission des messages est distribué de façon exponentielle. Les messages arrivant à des moments où le canal est occupé se voient refuser le service.

Définir

Р zan - la probabilité d'occupation du canal de communication (facteur de charge relative)

Q- bande passante relative

A est la bande passante absolue de la branche de communication

4. La branche internodale du réseau de communication secondaire a n = 4 canaux. Le flux de messages arrivant pour transmission sur les canaux de la branche de communication a un débit de = 8 messages par seconde. Le temps de transmission moyen d'un message est t = 0,1 seconde Un message arrivant au moment où tous les n canaux sont occupés reçoit un échec de transmission le long de la branche de communication. Trouver les caractéristiques du CMO :

ACTIVITÉ 3

Système monocanal avec attente

Considérons maintenant un QS monocanal avec attente. Le système de file d'attente a un canal. Le flux entrant de demandes de service est le flux le plus simple avec intensité. L'intensité du flux de service est égale (c'est-à-dire qu'en moyenne, un canal continuellement occupé émettra des demandes de service). La durée de service est une variable aléatoire soumise à une loi de distribution exponentielle. Le flux de service est le flux d'événements de Poisson le plus simple. Une demande qui arrive à un moment où le canal est occupé est mise en file d'attente et attend le service. Ce QS est le plus courant en modélisation. Avec un ou un autre degré d'approximation, il peut être utilisé pour simuler presque n'importe quel nœud d'un réseau local (LAN).

Supposons que peu importe le nombre de requêtes entrant dans l'entrée du système de service, ce système (file d'attente + clients servis) ne peut pas répondre à plus de N-exigences (demandes), c'est-à-dire que les clients qui ne tombent pas dans la période d'attente sont forcés d'être servis ailleurs. Système M/M/1/N. Enfin, la source qui génère les demandes de service a une capacité illimitée (infiniment grande). Le graphe d'état QS dans ce cas a la forme illustrée à la figure 3

Figure 3. Graphique des états d'un QS monocanal avec attente (schéma de mort et de reproduction)

Les états QS ont l'interprétation suivante :

S 0 - "le canal est libre" ;

S 1 - "le canal est occupé" (il n'y a pas de file d'attente);

S 2 - "le canal est occupé" (une application est dans la file d'attente) ;

S n - "le canal est occupé" (n -1 applications sont dans la file d'attente) ;

S N - "le canal est occupé" (N - 1 applications sont dans la file d'attente).

Le processus stationnaire dans ce système sera décrit par le système d'équations algébriques suivant :

où p=facteur de charge

n - numéro d'état.

La solution du système d'équations ci-dessus pour notre modèle QS a la forme :

La valeur initiale de la probabilité pour un QS avec une longueur de file d'attente limitée

Pour un QS avec une file d'attente infinie H =? :

P 0 \u003d 1- s (3.4.7)

Il est à noter que la satisfaction de la condition de stationnarité pour ce QS n'est pas nécessaire, puisque le nombre d'applications admises au système serveur est contrôlé en introduisant une restriction sur la longueur de la file d'attente, qui ne peut pas dépasser (N - 1), et non par le rapport entre les intensités du flux d'entrée, c'est-à-dire pas par le rapport c = l/m.

Contrairement au système monocanal, qui a été considéré ci-dessus et avec une file d'attente illimitée, dans ce cas, la distribution stationnaire du nombre de requêtes existe pour toutes les valeurs finies du facteur de charge c.

Déterminons les caractéristiques d'un QS monocanal avec attente et longueur de file limitée égale à (N - 1) (M/M/1/N), ainsi que pour un QS monocanal avec buffer de capacité illimitée (M/M/1/?). Pour un QS avec une file d'attente infinie, la condition avec<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) la probabilité de refus de service de la demande :

L'une des caractéristiques les plus importantes des systèmes dans lesquels des requêtes peuvent être perdues est la probabilité P loss qu'une requête arbitraire soit perdue. Dans ce cas, la probabilité de perdre une demande arbitraire coïncide avec la probabilité qu'à un moment arbitraire toutes les places d'attente soient occupées, c'est-à-dire la formule P de k \u003d P H est valide

2) débit relatif du système :

Pour CMO avec illimitéème file d'attente q=1, parce que toutes les demandes seront servies

3) bande passante absolue :

4) le nombre moyen d'applications dans le système :

L S avec file d'attente illimitée

5) temps de séjour moyen d'une application dans le système :

Pour file d'attente illimitée

6) la durée moyenne du séjour du client (de l'application) dans la file d'attente :

Avec file d'attente illimitée

7) le nombre moyen d'applications (clients) dans la file d'attente (longueur de la file d'attente) :

avec file d'attente illimitée

En comparant les expressions du temps d'attente moyen dans la file d'attente T pt et la formule de la longueur moyenne de la file d'attente L pt, ainsi que le temps de séjour moyen des requêtes dans le système T S et le nombre moyen de requêtes dans le système L S , on voit que

L och \u003d l * T och L s \u003d l * T s

Notez que ces formules sont également valables pour de nombreux systèmes de file d'attente plus généraux que le système M/M/1 considéré et sont appelées formules de Little. L'importance pratique de ces formules réside dans le fait qu'elles éliminent la nécessité de calculer directement les valeurs de T och et T s avec une valeur connue des valeurs de L och et L s et vice versa.

Tâches pour monocanal CMOavec attente, Avecanticipation etlongueur de file d'attente limitée

1. Étant donné un QS à une seule ligne avec un accumulateur de file d'attente illimité. Les candidatures arrivent toutes les t =14 secondes. Le temps de transmission moyen d'un message est de t=10 secondes. Les messages arrivant à des moments où le canal de desserte est occupé sont reçus dans la file d'attente sans la quitter jusqu'au début du service.

Déterminez les indicateurs de performance suivants :

2. La branche de communication internodale, qui a un canal et un lecteur de file d'attente pour m=3 messages en attente (N-1=m), reçoit le flux de messages le plus simple avec un débit de n=5 messages. en sec.. Le temps de transmission du message est distribué selon la loi exponentielle. Le temps de transmission moyen d'un message est de 0,1 seconde. Les messages arrivant à des moments où le canal de desserte est occupé à transmettre un message précédemment reçu et qu'il n'y a pas d'espace libre dans le lecteur sont rejetés.

Р otk - la probabilité de ne pas recevoir un message

L syst - le nombre total moyen de messages dans la file d'attente et transmis le long de la branche de communication

T och - le temps moyen pendant lequel le message reste dans la file d'attente avant le début de la transmission

T syst - le temps total moyen passé par un message dans le système, la somme du temps d'attente moyen dans la file d'attente et le temps de transmission moyen

Q- bande passante relative

A est le débit absolu

3. La branche internodale du réseau de communication secondaire, qui a un canal et une mémoire de file d'attente pour m = 4 (N-1=4) messages en attente, reçoit le flux de messages le plus simple avec un débit de = 8 messages par seconde. Le temps de transmission des messages est distribué de façon exponentielle. Le temps de transmission moyen d'un message est t = 0,1 seconde. Les messages arrivant à des moments où le canal de desserte est occupé à transmettre un message précédemment reçu et qu'il n'y a pas d'espace libre sur le lecteur sont refusés dans la file d'attente.

P otk - la probabilité d'échec de réception d'un message à transmettre sur le canal de communication de la branche internodale;

L och - le nombre moyen de messages dans la file d'attente vers la branche de communication du réseau secondaire de la file d'attente ;

L syst - le nombre total moyen de messages dans la file d'attente et transmis via la branche de communication du réseau secondaire;

Toch - le temps moyen pendant lequel le message reste dans la file d'attente avant le début de la transmission ;

Р zan - la probabilité d'occupation du canal de communication (coefficient de charge relative du canal);

Q est la capacité relative de la branche internodale ;

A est la capacité absolue de la branche internodale ;

4. La branche de communication internodale, qui a un canal et un lecteur de file d'attente pour m = 2 messages en attente, reçoit le flux de messages le plus simple avec une intensité de n = 4 messages. en sec.. Le temps de transmission du message est distribué selon la loi exponentielle. Le temps de transmission moyen d'un message est de 0,1 seconde. Les messages arrivant à des moments où le canal de desserte est occupé à transmettre un message précédemment reçu et qu'il n'y a pas d'espace libre dans le lecteur sont rejetés.

Déterminer les indicateurs de performance suivants de la branche communication :

Р otk - la probabilité de ne pas recevoir un message

L och - le nombre moyen de messages dans la file d'attente de la branche de communication

L syst - le nombre total moyen de messages dans la file d'attente et transmis le long de la branche de communication

T och - le temps moyen pendant lequel le message reste dans la file d'attente avant le début de la transmission

T syst - le temps total moyen passé par un message dans le système, la somme du temps d'attente moyen dans la file d'attente et le temps de transmission moyen

Р zan - la probabilité d'occupation du canal de communication (coefficient de charge relative du canal c)

Q- bande passante relative

A est le débit absolu

5. La branche internodale du réseau de communication secondaire, qui a un canal et une file d'attente de stockage illimitée de messages en attente, reçoit le flux de messages le plus simple avec une intensité de n = 0,06 messages par seconde. Temps de transmission moyen d'un message t = 10 secondes. Les messages arrivant à des moments où le canal de communication est occupé sont reçus dans la file d'attente et ne la quittent qu'au début du service.

Déterminez les indicateurs de performance suivants de la branche de communication du réseau secondaire :

L och - le nombre moyen de messages dans la file d'attente de la branche de communication ;

L syst - le nombre total moyen de messages dans la file d'attente et transmis le long de la branche de communication ;

Toch - le temps moyen passé par un message dans la file d'attente ;

T syst est le temps total moyen passé par un message dans le système, qui est la somme du temps d'attente moyen dans la file d'attente et du temps de transmission moyen ;

Р zan - la probabilité d'occupation du canal de communication (le coefficient de la charge relative du canal);

Q est la capacité relative de la branche internodale ;

A - débit absolu de la branche internodale

6. Étant donné un QS à une ligne avec un accumulateur de file d'attente illimité. Les candidatures arrivent toutes les t =13 secondes. Temps de transmission moyen par message

t=10 secondes. Les messages arrivant à des moments où le canal de desserte est occupé sont reçus dans la file d'attente sans la quitter jusqu'au début du service.

Déterminez les indicateurs de performance suivants :

L och - le nombre moyen de messages dans la file d'attente

L syst - le nombre total moyen de messages dans la file d'attente et transmis le long de la branche de communication

T och - le temps moyen pendant lequel le message reste dans la file d'attente avant le début de la transmission

T syst - le temps total moyen passé par un message dans le système, la somme du temps d'attente moyen dans la file d'attente et le temps de transmission moyen

Р zan - probabilité d'occupation (coefficient de charge relative du canal c)

Q- bande passante relative

A est le débit absolu

7. Un poste de diagnostic spécialisé est un QS monocanal. Le nombre de parkings pour voitures en attente de diagnostic est limité et égal à 3 [(N - 1) = 3]. Si tous les parkings sont occupés, c'est-à-dire qu'il y a déjà trois voitures dans la file d'attente, la voiture suivante arrivée pour le diagnostic n'entre pas dans la file d'attente de service. Le flux de voitures arrivant pour diagnostic est distribué selon la loi de Poisson et a une intensité = 0,85 (voitures par heure). Le temps de diagnostic automobile est distribué selon la loi exponentielle et est égal à 1,05 heure en moyenne.

Il s'agit de déterminer les caractéristiques probabilistes du poste de diagnostic fonctionnant en mode stationnaire : P 0 , P 1 , P 2 , P 3 , P 4 , P ouvert, q, A, L och, L sys, T och, T sis

ACTIVITÉ 4

QS multicanal avec attente, avec attente et longueur de file d'attente limitée

Considérez un système de file d'attente multicanal avec attente. Ce type de QS est souvent utilisé lors de la modélisation de groupes de terminaux d'abonnés LAN fonctionnant en mode en ligne. Le processus de mise en file d'attente est caractérisé par ce qui suit : les flux d'entrée et de sortie sont Poisson avec des intensités et respectivement ; pas plus de n clients peuvent être servis en parallèle. Le système dispose de n canaux de service. Le temps de service moyen par client est de 1/m pour chaque canal. Ce système fait également référence au processus de mort et de reproduction.

c=l/nm - le rapport de l'intensité du flux entrant à l'intensité totale du service, est le facteur de charge du système

(Avec<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

où Р 0 est la probabilité d'un état libre de tous les canaux avec une file d'attente illimitée, k est le nombre d'applications.

si l'on accepte c=l / m, alors P 0 peut être déterminé pour une file d'attente illimitée :

Pour file d'attente limitée :

où m est la longueur de la file d'attente

Avec file d'attente illimitée :

Débit relatif q=1,

Bande passante absolue A \u003d l,

Nombre moyen de canaux occupés Z=A/m

Avec file d'attente limitée

1 La branche inter-nodale du réseau de communication secondaire comporte n = 4 canaux. Le flux de messages arrivant pour transmission sur les canaux de la branche de communication a un débit de = 8 messages par seconde. Le temps moyen t = 0,1 pour la transmission d'un message par chaque canal de communication est t/n = 0,025 secondes. Le temps d'attente des messages dans la file d'attente est illimité. Trouver les caractéristiques du CMO :

R otk - la probabilité d'échec de la transmission des messages ;

Q est le débit relatif de la branche de communication ;

A est la bande passante absolue de la branche de communication ;

Z est le nombre moyen de canaux occupés ;

L och - le nombre moyen de messages dans la file d'attente ;

T exp - temps d'attente moyen ;

T syst - le temps total moyen passé par les messages dans la file d'attente et la transmission le long de la branche de communication.

2. L'atelier mécanique de l'usine à trois postes (canaux) effectue des réparations de mécanisation à petite échelle. Le flux de mécanismes défectueux arrivant à l'atelier est de Poisson et a une intensité de = 2,5 mécanismes par jour, le temps moyen de réparation pour un mécanisme est distribué selon la loi exponentielle et est égal à = 0,5 jours. Supposons qu'il n'y ait pas d'autre atelier dans l'usine et que, par conséquent, la file d'attente de mécanismes devant l'atelier puisse s'allonger presque indéfiniment. Il est nécessaire de calculer les valeurs limites suivantes des caractéristiques probabilistes du système :

Probabilités des états du système ;

Le nombre moyen d'applications dans la file d'attente de service ;

Le nombre moyen d'applications dans le système ;

La durée moyenne de l'application dans la file d'attente ;

La durée moyenne de séjour d'une application dans le système.

3. La branche internodale du réseau de communication secondaire comporte n=3 canaux. Le flux de messages arrivant pour transmission par les canaux de la branche de communication a une intensité de n = 5 messages par seconde. Le temps de transmission moyen d'un message est t = 0,1 , t/n = 0,033 s Jusqu'à m = 2 messages peuvent être stockés dans le lecteur de file d'attente des messages en attente. Un message qui arrive à un moment où toutes les places de la file d'attente sont occupées reçoit un rejet de transmission sur la branche de communication. Trouvez les caractéristiques du QS : Р ref est la probabilité d'échec de la transmission des messages, Q est le débit relatif, A est le débit absolu, Z est le nombre moyen de canaux occupés, L och est le nombre moyen de messages dans la file d'attente, T exp est le temps d'attente moyen, T sys est le temps total moyen pendant lequel le message reste dans la file d'attente et sa transmission le long de la branche de communication.

ACTIVITÉ 5

QS fermé

Considérons le modèle de desserte du parc machine, qui est un modèle de système de file d'attente fermée. Jusqu'à présent, nous n'avons considéré que de tels systèmes de file d'attente pour lesquels l'intensité du flux entrant de requêtes ne dépend pas de l'état du système. Dans ce cas, la source des sinistres est externe au QS et génère un flux illimité de sinistres. Considérez les systèmes de file d'attente pour lesquels dépend de l'état du système, où la source des exigences est interne et génère un flux limité de demandes. Par exemple, un parc machine composé de N machines est entretenu par une équipe de R mécaniciens (N > R), et chaque machine ne peut être entretenue que par un seul mécanicien. Ici, les machines sont des sources d'exigences (demandes de service), et les mécaniciens sont des canaux de service. Une machine défaillante après entretien est utilisée conformément à sa destination et devient une source potentielle d'exigences d'entretien. Évidemment, l'intensité dépend du nombre de voitures actuellement en service (N - k) et du nombre de voitures en cours d'entretien ou en file d'attente (k). Dans le modèle considéré, la capacité de la source d'exigences doit être considérée comme limitée. Le flux entrant de besoins provient d'un nombre limité de machines en fonctionnement (N - k), qui tombent en panne à des moments aléatoires et nécessitent une maintenance. De plus, chaque machine de (N - k) est en fonctionnement. Génère un flux de demande de Poisson avec une intensité X indépendamment des autres objets, le flux entrant total a une intensité. Une requête qui entre dans le système au moment où au moins un canal est libre est immédiatement envoyée en service. Si une exigence trouve tous les canaux occupés à servir d'autres exigences, elle ne quitte pas le système, mais se met en file d'attente et attend jusqu'à ce que l'un des canaux se libère. Ainsi, dans un système de file d'attente fermée, le flux entrant de demandes est formé à partir du flux sortant. L'état S k du système est caractérisé par le nombre total de requêtes en cours de traitement et dans la file d'attente, égal à k. Pour le système fermé considéré, évidemment, k = 0, 1, 2, ... , N. De plus, si le système est dans l'état S k , alors le nombre d'objets en fonctionnement est (N - k). Si - l'intensité du flux de besoins par machine, alors :

Le système d'équations algébriques décrivant le fonctionnement d'un QS fermé en mode stationnaire est le suivant :

En résolvant ce système, nous trouvons la probabilité du k-ième état :

La valeur de P 0 est déterminée à partir de la condition de normalisation des résultats obtenus par les formules pour P k , k = 0, 1, 2, ... , N. Définissons les caractéristiques probabilistes suivantes du système :

Nombre moyen de requêtes dans la file d'attente de service :

Nombre moyen de requêtes dans le système (en service et en file d'attente)

nombre moyen de mécaniciens (canaux) "inactifs" faute de travail

Le taux d'indisponibilité de l'objet desservi (machine) dans la file d'attente

Taux d'utilisation des objets (machines)

Taux d'indisponibilité des canaux de service (mécanique)

Temps d'attente moyen pour le service (temps d'attente du service dans la file d'attente)

Problème QS fermé

1. Que deux ingénieurs de la même productivité soient affectés à l'entretien de dix ordinateurs personnels (PC). Le flux de pannes (dysfonctionnements) d'un ordinateur est de Poisson avec une intensité = 0,2. Le temps de service d'un PC obéit à une loi exponentielle. Le temps de maintenance moyen d'un PC par un ingénieur est de : = 1,25 heures. Les options d'organisation de service suivantes sont disponibles :

Les deux ingénieurs servent les dix ordinateurs, donc si le PC tombe en panne, l'un des ingénieurs libres le sert, dans ce cas R = 2, N = 10 ;

Chacun des deux ingénieurs maintient cinq PC qui lui sont assignés. Dans ce cas, R = 1, N = 5.

Il est nécessaire de choisir la meilleure option pour organiser la maintenance du PC.

Il faut définir toutes les probabilités d'états P k : P 1 - P 10, sachant que et à partir des résultats du calcul de P k, on calcule P 0

ACTIVITÉ 6

Calcul du trafic.

La théorie du télétrafic est une partie de la théorie des files d'attente. Les bases de la théorie du télétrafic ont été posées par le scientifique danois A.K. Erlang. Ses œuvres ont été publiées en 1909-1928. Donnons des définitions importantes utilisées dans la théorie du télétrafic (TT). Le terme "trafic" (en anglais, trafic) correspond au terme "charge téléphonique". Il implique la charge créée par le flux d'appels, de demandes, de messages arrivant aux entrées du QS. Le volume de trafic est appelé la valeur de l'intervalle de temps total, entier, manqué par l'une ou l'autre ressource, pendant lequel cette ressource a été occupée pendant la période de temps analysée. Une unité de travail peut être considérée comme une deuxième occupation d'une ressource. Parfois, vous pouvez lire des heures, et parfois seulement des secondes ou des heures. Cependant, les recommandations de l'UIT donnent la dimension du volume de trafic en heures d'erlango. Pour comprendre la signification d'une telle unité de mesure, un autre paramètre de trafic doit être pris en compte - l'intensité du trafic. Dans ce cas, ils parlent souvent de l'intensité moyenne du trafic (charge) sur un pool (ensemble) de ressources donné. Si à chaque instant t d'un intervalle donné (t 1 ,t 2) le nombre de ressources de cet ensemble occupées par le trafic de desserte est égal à A(t), alors l'intensité moyenne du trafic sera

La valeur de l'intensité du trafic est caractérisée comme le nombre moyen de ressources occupées par le trafic dans un intervalle de temps donné. L'unité de mesure de l'intensité de la charge est un Erlang (1 Erl, 1 E), c'est-à-dire 1 erlang est l'intensité du trafic qui nécessite le plein emploi d'une ressource, ou, en d'autres termes, à laquelle le travail d'une seconde est effectué par la ressource - occupation pendant une durée d'une seconde. Dans la littérature américaine, on trouve parfois une autre unité de mesure appelée CCS-Centrum (ou cent) Calls Second (hectosecond occupations). Le numéro CCS reflète le temps d'occupation des serveurs par intervalles de 100 secondes en 1 heure. L'intensité mesurée en CCS peut être convertie en Erlangs en utilisant la formule 36CCS=1 Erl.

Le trafic généré par une source et exprimé en heures-sessions est égal au produit du nombre de tentatives d'appel c pendant un certain intervalle de temps T et de la durée moyenne d'une tentative t : y = c t (h-h). Le trafic peut être calculé de trois manières différentes :

1) soit le nombre d'appels c par heure soit 1800, et la durée moyenne de la leçon t = 3 minutes, alors Y = 1800 appels. /h 0,05 h = 90 Erl ;

2) en fixant les durées t i de toutes les n occupations des sorties d'un certain faisceau pendant le temps T, alors le trafic est déterminé comme suit :

3) soit pendant le temps T, l'observation est effectuée à intervalles réguliers sur le nombre de sorties occupées simultanément d'un certain faisceau, selon les résultats des observations, une fonction échelon du temps x(t) est construite (Figure 8).

Figure 8. Nombre de sorties de faisceau occupées simultanément

Le trafic pendant le temps T peut être estimé comme la valeur moyenne de x(t) sur ce temps :

où n est le nombre d'échantillons de sorties occupées simultanément. La valeur de Y est le nombre moyen de sorties de faisceau occupées simultanément pendant le temps T.

Fluctuations du trafic. Le trafic des réseaux téléphoniques secondaires fluctue fortement dans le temps. Pendant la journée de travail, la courbe de trafic présente deux voire trois pics (Figure 9).

Figure 9. Fluctuations du trafic au cours de la journée

L'heure de la journée pendant laquelle le trafic de longue durée est le plus important est appelée l'heure de pointe (BUSH). La connaissance du trafic dans le CNN est d'une importance fondamentale, car elle détermine le nombre de canaux (lignes), la quantité d'équipements des stations et des nœuds. Le trafic d'un même jour de la semaine connaît des fluctuations saisonnières. Si le jour de la semaine est un jour pré-férié, la VAN de ce jour est supérieure à celle du jour suivant le jour férié. Si le nombre de services pris en charge par le réseau augmente, le trafic augmente également. Par conséquent, il est difficile de prédire avec suffisamment de certitude l'occurrence des pics de trafic. Le trafic est étroitement surveillé par les organismes d'administration et de conception du réseau. Les règles de mesure du trafic sont élaborées par l'UIT-T et sont utilisées par les administrations des réseaux nationaux afin de répondre aux exigences de qualité de service tant pour les abonnés de leur propre réseau que pour les abonnés d'autres réseaux qui y sont connectés. La théorie du télétrafic ne peut être utilisée pour des calculs pratiques de pertes ou de volume d'équipement d'une station (nœud) que si le trafic est stationnaire (statistiquement stable). Cette condition est approximativement satisfaite par le trafic dans le CNN. La quantité de charge reçue par jour sur le PBX affecte la prévention et la réparation des équipements. L'inégalité de la charge sur la station pendant la journée est déterminée par le coefficient de concentration

Une définition plus rigoureuse de NNN est la suivante. La Recommandation UIT E.500 prescrit d'analyser les données d'intensité sur 12 mois, d'en sélectionner les 30 jours les plus chargés, de trouver les heures les plus chargées de ces jours et de faire la moyenne des résultats de mesure d'intensité sur ces intervalles. Ce calcul de l'intensité du trafic (charge) s'appelle l'estimation normale de l'intensité du trafic à l'heure chargée ou au niveau A. Une estimation plus stricte peut être calculée en moyenne sur les 5 jours les plus chargés de la période de 30 jours sélectionnée. Une telle évaluation est appelée une augmentation ou une évaluation du niveau de B.

Le processus de création de trafic. Comme tout utilisateur du réseau téléphonique le sait, toutes les tentatives d'établissement d'une connexion avec l'abonné appelé ne se terminent pas avec succès. Parfois, vous devez faire plusieurs tentatives infructueuses avant que la connexion souhaitée ne soit établie.

Figure 10. Diagramme des événements lors de l'établissement d'une connexion entre abonnés

Considérons les événements possibles lors de la simulation de l'établissement d'une connexion entre les abonnés A et B (Figure 10). Les données statistiques sur les appels dans les réseaux téléphoniques sont les suivantes : la part des appels aboutis est de 70 à 50 %, la part des appels échoués est de 30 à 50 %. Toute tentative de l'abonné occupe l'entrée du QS. En cas de tentatives réussies (lorsque la conversation a eu lieu), le temps d'occupation des dispositifs de commutation qui établissent les connexions entre les entrées et les sorties est plus long qu'en cas de tentatives infructueuses. L'abonné peut interrompre les tentatives de connexion à tout moment. Les tentatives peuvent être causées par les raisons suivantes :

Numéro mal composé ;

Hypothèse d'erreur dans le réseau ;

Le degré d'urgence de la conversation;

Tentatives précédentes infructueuses ;

Connaître les habitudes de l'abonné B ;

Doute sur la numérotation correcte.

Une nouvelle tentative peut être tentée dans les circonstances suivantes :

Degrés d'urgence ;

Estimations des raisons de l'échec ;

Estimations de l'opportunité de tentatives répétées,

Estimations de l'intervalle acceptable entre les tentatives.

Le refus de réessayer peut être associé à un faible degré d'urgence. Il existe plusieurs types de trafic générés par les appels : entrant (offert) Y p et manqué Y p. Le trafic Y p comprend toutes les tentatives réussies et infructueuses, le trafic Y p, qui fait partie de Y p, comprend les tentatives réussies et une partie des tentatives infructueuses :

Y pr \u003d Y p + Y np,

où Y p - trafic conversationnel (utile) et Y np - trafic créé par des tentatives infructueuses. L'égalité Yp = Yp n'est possible que dans le cas idéal, s'il n'y a pas de pertes, d'erreurs d'appelants et pas de réponses d'abonnés appelés.

La différence entre les charges entrantes et manquées pendant une certaine période de temps sera la charge perdue.

Prévision de trafic. Les ressources limitées conduisent à la nécessité d'une extension progressive de la gare et du réseau. L'administration du réseau fait une prévision d'augmentation du trafic pendant la phase de développement, considérant que :

Le revenu est déterminé par la part du trafic transité Y p, - les coûts sont déterminés par la qualité de service au trafic le plus élevé ;

Une grande proportion de pertes (faible qualité) se produit dans de rares cas et est typique de la fin de la période de développement ;

Le plus grand volume de trafic manqué tombe sur les périodes où il n'y a pratiquement pas de pertes - si les pertes sont inférieures à 10%, les abonnés n'y répondent pas. Lors de la planification du développement des stations et du réseau, le concepteur doit répondre à la question, quelles sont les exigences pour la qualité de la fourniture de service (pour les pertes). Pour ce faire, il est nécessaire de mesurer les pertes de trafic selon les règles adoptées dans le pays.

Un exemple de mesure de trafic.

Tout d'abord, considérez comment vous pouvez afficher le fonctionnement d'un QS qui a plusieurs ressources qui desservent du trafic en même temps. Nous parlerons plus loin de ressources telles que les serveurs qui servent le flux d'applications ou d'exigences. L'un des moyens les plus visuels et les plus couramment utilisés pour décrire le processus de traitement des demandes par un pool de serveurs est un diagramme de Gantt. Ce graphe est un repère rectangulaire dont l'abscisse représente le temps et l'ordonnée représente des points discrets correspondant aux serveurs du pool. La figure 11 montre un diagramme de Gantt pour un système avec trois serveurs.

Dans les trois premiers intervalles de temps (nous les considérons comme une seconde), les premier et troisième serveurs sont occupés, les deux secondes suivantes - seulement la troisième, puis la seconde fonctionne pendant une seconde, puis la seconde et la première pendant deux secondes, et les deux dernières secondes - seulement la première.

Le schéma construit permet de calculer le volume de trafic et son intensité. Le diagramme ne montre que le trafic servi ou manqué, car il ne dit rien sur le fait que les demandes entrées dans le système n'ont pas pu être servies par les serveurs.

Le volume du trafic passé est calculé comme la longueur totale de tous les segments du diagramme de Gantt. Volume en 10 secondes :

Associez à chaque intervalle de temps porté en abscisse, un entier égal au nombre de serveurs occupés dans cet intervalle unique. Cette valeur A(t) est l'intensité instantanée. Pour notre exemple

A(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Trouvons maintenant l'intensité moyenne du trafic sur une période de 10 secondes

Ainsi, l'intensité moyenne du trafic transité par le système considéré de trois serveurs est égale à 1,5 Erl.

Principaux paramètres de charge

La communication téléphonique est utilisée par différentes catégories d'abonnés, qui se caractérisent par :

le nombre de sources de charge - N,

le nombre moyen d'appels d'une source dans un certain temps (HNN généralement) - s,

la durée moyenne d'une occupation du système de commutation lors du service d'un appel est t.

L'intensité de la charge sera

Définissons différentes sources d'appels. Par exemple,

Nombre moyen d'appels par téléphone de bureau par téléphone de bureau ;

Le nombre moyen d'appels depuis un appareil individuel d'appartement ; télétrafic de mise en file d'attente d'événements aléatoires

avec un décompte - le même de l'appareil à usage collectif;

avec ma - la même chose à partir d'une machine à sous;

avec sl - le même à partir d'une ligne de connexion.

Alors le nombre moyen d'appels d'une source est :

Il existe des données approximatives pour le nombre moyen d'appels d'une source de la catégorie correspondante :

3,5 - 5, \u003d 0,5 - 1, avec comptage \u003d 1,5 - 2, avec ma \u003d 15 - 30, avec sl \u003d 10 - 30.

Il existe les types de connexions suivants, qui, selon le résultat de la connexion, créent une charge téléphonique différente au poste :

k p - coefficient indiquant la proportion de connexions qui se sont terminées par une conversation ;

k c - connexions qui ne se sont pas terminées par une conversation en raison de l'occupation de l'abonné appelé;

k mais - coefficient exprimant la proportion de connexions qui ne se sont pas terminées par une conversation en raison de la non-réponse de l'abonné appelé ;

k osh - connexions qui ne se sont pas terminées par une conversation en raison d'erreurs de l'appelant ;

k de ceux-ci - appels qui ne se sont pas terminés par une conversation pour des raisons techniques.

En fonctionnement normal du réseau, les valeurs de ces coefficients sont égales à :

k p = 0,60-0,75 ; k c = 0,12-0,15 ; k mais = 0,08-0,12 ; kosh = 0,02-0,05 ; k ceux = 0,005-0,01.

La durée moyenne d'une leçon dépend des types de connexions. Par exemple, si la connexion s'est terminée par une conversation, la durée moyenne d'occupation des appareils t état sera égale à

où est la durée d'établissement de la connexion ;

cond. - la conversation qui a eu lieu ;

t in - la durée d'envoi d'un appel vers le poste téléphonique de l'abonné appelé;

t p - durée de la conversation

où t co - signal de réponse de la station ;

1,5n - temps de numérotation de l'abonné appelé (n - nombre de caractères dans le numéro);

t avec - le temps nécessaire pour établir une connexion en commutant les mécanismes et déconnecter la connexion après la fin de la conversation. Valeurs approximatives des grandeurs considérées :

t co \u003d 3 sec., t c \u003d 1-2,5 sec., t en \u003d 8-10 sec., t p \u003d 90-130 sec.

Les appels qui ne se terminent pas par une conversation créent également une charge téléphonique.

Le temps d'occupation moyen des appareils lorsque l'abonné appelé est occupé est égal à

où t est défini. déterminé par (4.2.3)

t buzzer - temps d'écoute du buzzer occupé, t buzzer =6sec.

La durée moyenne d'occupation des appareils lorsque l'abonné appelé ne répond pas est égale à

où t pv est le temps d'écoute du signal de commande de retour d'appel, t pv = 20 sec.

S'il n'y a pas eu de conversation en raison d'erreurs d'abonné, alors en moyenne t osh = 30 sec.

La durée des sessions qui ne se sont pas terminées par une conversation pour des raisons techniques n'est pas définie, car le pourcentage de telles sessions est faible.

De tout ce qui précède, il s'ensuit que la charge totale créée par un groupe de sources pour le NTT est égale à la somme des charges des différents types d'occupations.

où est un coefficient qui prend en compte les termes comme parts

Sur un réseau téléphonique avec une numérotation à sept chiffres, un central téléphonique automatique a été conçu, dont la composition structurelle des abonnés est la suivante:

N chr \u003d 4000, N ind \u003d 1000, N count \u003d 2000, N ma \u003d 400, N sl \u003d 400.

Le nombre moyen d'appels provenant d'une source au cours d'une heure chargée est

Par les formules (4.2.3) et (4.2.6) on trouve la charge

1.10.62826767 s = 785,2 Hz.

Durée moyenne des cours t selon la formule Y=Nct

t= Y/Nc= 2826767/7800*3,8=95,4 s.

Charger la tâche

1. Sur un réseau téléphonique à numérotation à sept chiffres, un central téléphonique automatique a été conçu, dont la composition structurelle des abonnés est la suivante:

N uchr \u003d 5000, N ind \u003d 1500, N count \u003d 3000, N ma \u003d 500, N sl \u003d 500.

Déterminer la charge arrivant à la station - Y, la durée moyenne d'occupation t, si l'on sait que

avec uchr \u003d 4, avec ind \u003d 1, avec count \u003d 2, avec ma \u003d 10, avec sl \u003d 12, t p \u003d 120 sec., t in \u003d 10 sec., k p \u003d 0,6, t avec \u003d 1 sec., \u 003d 1.1.

Hébergé sur Allbest.ru

Documents similaires

Le concept d'une variable aléatoire uniformément distribuée. Méthode congruente multiplicative. Modélisation de variables aléatoires continues et de distributions discrètes. Algorithme de simulation des relations économiques entre un prêteur et un emprunteur.

dissertation, ajouté le 01/03/2011


Concepts généraux de la théorie des files d'attente. Caractéristiques de la modélisation des systèmes de file d'attente. Graphes d'état QS, équations les décrivant. Caractéristiques générales des variétés de modèles. Analyse du système de file d'attente des supermarchés.

dissertation, ajouté le 17/11/2009


Éléments de la théorie des files d'attente. Modélisation mathématique des systèmes de file d'attente, leur classification. Modélisation de simulation de systèmes de file d'attente. Application pratique de la théorie, résolution de problèmes par des méthodes mathématiques.

dissertation, ajouté le 04/05/2011


Le concept de processus aléatoire. Tâches de la théorie des files d'attente. Classification des systèmes de file d'attente (QS). Modèle mathématique probabiliste. Influence de facteurs aléatoires sur le comportement d'un objet. QS monocanal et multicanal avec attente.

dissertation, ajouté le 25/09/2014


L'étude des aspects théoriques de la construction et du fonctionnement efficaces d'un système de file d'attente, ses principaux éléments, sa classification, ses caractéristiques et ses performances. Modélisation d'un système de file d'attente en langage GPSS.

dissertation, ajouté le 24/09/2010


Développement de la théorie de la programmation dynamique, de la planification des réseaux et de la gestion de la fabrication des produits. Composantes de la théorie des jeux dans les problèmes de modélisation des processus économiques. Éléments d'application pratique de la théorie des files d'attente.

travaux pratiques, ajouté le 01/08/2011


Concepts élémentaires sur les événements aléatoires, les quantités et les fonctions. Caractéristiques numériques des variables aléatoires. Types d'asymétrie des distributions. Évaluation statistique de la distribution des variables aléatoires. Résolution de problèmes d'identification structurale-paramétrique.

dissertation, ajouté le 06/03/2012


Modélisation du processus de file d'attente. Différents types de canaux de file d'attente. Solution du modèle de file d'attente à canal unique avec échecs. Densité de distribution de durée de service. Définition du débit absolu.

test, ajouté le 15/03/2016


Caractéristiques fonctionnelles du système de file d'attente dans le domaine du transport routier, sa structure et ses principaux éléments. Indicateurs quantitatifs de la qualité du fonctionnement du système de file d'attente, de la procédure et des principales étapes de leur détermination.

travail de laboratoire, ajouté le 11/03/2011


Fixer l'objectif de la modélisation. Identification d'objets réels. Sélection du type de modèles, schéma mathématique. Construction d'un modèle stochastique continu. Concepts de base de la théorie des files d'attente. Définir le flux des événements. Énoncé des algorithmes.