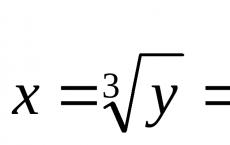Hogyan határozzuk meg a függvényértékek halmazát. A funkciók köre a USE problémákban

Egyik változónak a másiktól való függését nevezzük funkcionális függőség. Függőségi változó y változótól x hívott funkció, ha minden érték x egyetlen értéknek felel meg y.

Kijelölés:

Változó x független változónak, ill érv, és a változó y- függő. Azt mondják y függvénye x. Jelentése y, amely megfelel a megadott értéknek x, hívott függvény értéke.

Minden érték, amit elfogad x, forma egy függvény tartománya; az összes szükséges értéket y, forma függvényértékek halmaza.

Megnevezések:

D(f)- érvértékek. E(f)- függvényértékek. Ha egy függvényt egy képlet ad meg, akkor a definíciós tartomány a változó összes értékéből áll, amelyre ennek a képletnek van értelme.

Függvénygrafikon a koordinátasíkon lévő azon pontok halmaza, amelyek abszcisszái megegyeznek az argumentum értékeivel, és amelyek ordinátái megegyeznek a függvény megfelelő értékeivel. Ha valamilyen érték x=x 0 több értékkel egyezik (nem csak egy) y, akkor az ilyen megfeleltetés nem függvény. Ahhoz, hogy egy koordinátasíkon egy ponthalmaz egy bizonyos függvény grafikonja legyen, szükséges és elegendő, hogy az Oy tengellyel párhuzamos bármely egyenes legfeljebb egy pontban metszi a gráfot.

Funkció megadásának módszerei

1) A funkció beállítható elemzőleg képlet formájában. Például,

2) A függvény sok párból álló táblázattal adható meg (x; y).

3) A funkció grafikusan megadható. Értékpárok (x; y) koordinátasíkon vannak ábrázolva.

A függvény monotonitása

Funkció f(x) hívott növekvő adott numerikus intervallumon, ha az argumentum nagyobb értéke a függvény nagyobb értékének felel meg. Képzelje el, hogy egy bizonyos pont balról jobbra mozog a grafikonon. Ekkor a pont úgy tűnik, hogy „felmászik” a grafikonon.

Funkció f(x) hívott csökkenő adott numerikus intervallumon, ha az argumentum nagyobb értéke a függvény kisebb értékének felel meg. Képzelje el, hogy egy bizonyos pont balról jobbra mozog a grafikonon. Ekkor a pont úgy tűnik, hogy „legurul” a grafikonon.

Olyan függvényt hívunk meg, amely egy adott numerikus intervallumon csak növekszik vagy csak csökken monoton ezen az intervallumon.

A függvény nullái és az állandó előjel intervallumai

Értékek x, ahol y=0, hívott függvény nullák. Ezek a függvénygráf és az Ox tengellyel való metszéspontjainak abszcisszán.

Ilyen értéktartományok x, amelyen a függvény értékeit y vagy csak pozitív vagy csak negatív hívják a függvény állandó előjelének intervallumai.

Páros és páratlan függvények

Egyenletes funkció
1) A definíciós tartomány szimmetrikus a (0; 0) ponthoz képest, vagyis ha a pont a a definíció tartományába tartozik, akkor a pont -a szintén a definíció tartományába tartozik.
2) Bármilyen értékre x f(-x)=f(x)
3) Egy páros függvény grafikonja szimmetrikus az Oy tengelyre.

Páratlan funkció a következő tulajdonságokkal rendelkezik:
1) A definíciós tartomány szimmetrikus a (0; 0) pontra.
2) bármilyen értékre x, amely a definíció, az egyenlőség tartományába tartozik f(-x)=-f(x)
3) Egy páratlan függvény grafikonja szimmetrikus az origóhoz (0; 0).

Nem minden függvény páros vagy páratlan. Funkciók Általános nézet sem nem párosak, sem nem páratlanok.

Periodikus funkciók

Funkció f periodikusnak nevezzük, ha van olyan szám, hogy bármely x a definíció tartományából az egyenlőség f(x)=f(x-T)=f(x+T). T a függvény periódusa.

Minden periodikus függvénynek végtelen számú periódusa van. A gyakorlatban általában a legkisebb pozitív időszakot veszik figyelembe.

A periodikus függvény értékei a periódussal megegyező intervallum után ismétlődnek. Ezt grafikonok készítésekor használják.

Gyakran a problémák megoldásának részeként egy függvény számos értékét kell keresnünk egy definíciós tartományon vagy egy szegmensen. Például ezt a megoldáskor kell megtenni különböző típusok egyenlőtlenségek, kifejezések értékelései stb.

Ennek az anyagnak a részeként elmondjuk, hogy mi a függvény értéktartománya, megadjuk a főbb módszereket, amelyekkel kiszámítható, és elemezzük a problémákat. változó mértékben nehézségek. Az egyértelműség kedvéért az egyes rendelkezéseket grafikonokkal illusztráljuk. A cikk elolvasása után átfogó képet kap egy funkció tartományáról.

Kezdjük az alapvető definíciókkal.

1. definíció

Egy y = f (x) függvény értékkészlete egy bizonyos x intervallumon az összes érték halmaza, amelyet ez a függvény felvesz, amikor az összes x ∈ X értéket iterálja.

2. definíció

Az y = f (x) függvény értéktartománya az összes érték halmaza, amelyet felvehet, amikor az x ∈ (f) tartományból keresi az x értékeit.

Egy bizonyos függvény értéktartományát általában E (f) jelöli.

Kérjük, vegye figyelembe, hogy egy függvény értékkészletének fogalma nem mindig azonos az értéktartományával. Ezek a fogalmak csak akkor lesznek ekvivalensek, ha az x értékeinek intervalluma egy értékkészlet megtalálásakor egybeesik a függvény definíciós tartományával.

Szintén fontos különbséget tenni az értéktartomány és az x változó elfogadható értékeinek tartománya között a jobb oldali y = f (x) kifejezéshez. Az f (x) kifejezés megengedett x értékeinek tartománya lesz a függvény definíciós tartománya.

Az alábbiakban egy illusztráció néhány példát mutat be. A kék vonalak függvénygrafikonok, a piros vonalak aszimptoták, a piros pontok és az ordináta tengelyen lévő vonalak függvénytartományok.

Nyilvánvaló, hogy egy függvény értéktartományát úgy kaphatjuk meg, ha a függvény grafikonját az O y tengelyre vetítjük. Ezenkívül képviselhet egyetlen számot vagy számkészletet, szegmenst, intervallumot, nyílt sugarat, numerikus intervallumok unióját stb.

Nézzük meg a függvény értéktartományának megtalálásának fő módjait.

Kezdjük azzal, hogy meghatározzuk az y = f (x) folytonos függvény értékkészletét egy bizonyos [ a ; b ] . Tudjuk, hogy egy adott szakaszon folytonos függvény eléri rajta a minimumát és maximumát, vagyis a legnagyobb m a x x ∈ a ; b f (x) és a legkisebb érték m i n x ∈ a ; b f (x) . Ez azt jelenti, hogy egy m i n x ∈ a szakaszt kapunk; bf(x); m a x x ∈ a ; b f (x) , amely az eredeti függvény értékkészleteit fogja tartalmazni. Ezután már csak meg kell találnunk a jelzett minimum és maximum pontot ezen a szakaszon.

Vegyünk egy feladatot, amelyben meg kell határoznunk az arcszinusz értékek tartományát.

1. példa

Feltétel: keresse meg az y = a r c sin x értéktartományt.

Megoldás

Általános esetben az arcszinusz definíciós tartománya a [ - 1 ; 1 ] . Meg kell határoznunk rajta a megadott függvény legnagyobb és legkisebb értékét.

y " = a r c sin x " = 1 1 - x 2

Tudjuk, hogy a függvény deriváltja pozitív lesz a [-1] intervallumban található x összes értékére; 1 ], vagyis a teljes definíciós tartományban az arcszinusz függvény növekedni fog. Ez azt jelenti, hogy a legkisebb értéket akkor veszi fel, ha x egyenlő -1-gyel, a legnagyobb értéket pedig akkor, ha x egyenlő 1-gyel.

m i n x ∈ - 1; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2

Így az arcszinusz függvény értéktartománya egyenlő lesz: E (a r c sin x) = - π 2; π 2.

Válasz: E (a r c sin x) = - π 2 ; π 2

2. példa

Feltétel: számítsa ki az y = x 4 - 5 x 3 + 6 x 2 értéktartományt az adott intervallumon [ 1 ; 4 ] .

Megoldás

Csak annyit kell tennünk, hogy kiszámítjuk a függvény legnagyobb és legkisebb értékét egy adott intervallumban.

Az extrém pontok meghatározásához a következő számításokat kell elvégezni:

y " = x 4 - 5 x 3 + 6 x 2 " = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1; 4 és l és 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1, 16 ∈ 1; 4 x 3 = 15 + 33 8 ≈ 2, 59 ∈ 1; 4

Most keressük meg az adott függvény értékeit a szakasz és az x 2 = 15 - 33 8 pontok végén; x 3 = 15 + 33 8:

y (1) = 1 4 - 5 1 3 + 6 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 ≉ + 165 33 512 2. 08 y 15 + 33 8 = 15 + 33 8 4 - 5 · 15 + 33 8 3 + 6 · 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 év (4) = 4 4 - 5 4 3 + 6 4 2 = 32

Ez azt jelenti, hogy a függvényértékek halmazát a 117 - 165 33 512 szegmens határozza meg; 32.

Válasz: 117 - 165 33 512 ; 32 .

Térjünk tovább az y = f (x) folytonos függvény értékkészletének megkeresésére az (a ; b) és a intervallumokban; + ∞ , - ∞ ; b , - ∞ ; + ∞ .

Kezdjük azzal, hogy meghatározzuk a legnagyobb és legkisebb pontokat, valamint a növekedési és csökkentési intervallumokat egy adott intervallumon. Ezt követően egyoldalú határértékeket kell kiszámítanunk az intervallum végén és/vagy határértékeket a végtelenben. Más szóval, meg kell határoznunk a függvény viselkedését adott feltételek mellett. Ehhez minden szükséges adattal rendelkezünk.

3. példa

Feltétel: számítsuk ki az y = 1 x 2 - 4 függvény tartományát a (- 2 ; 2) intervallumon.

Megoldás

Határozza meg egy függvény legnagyobb és legkisebb értékét egy adott szakaszon

y " = 1 x 2 - 4 " = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ ( - 2 ; 2)

0-val egyenlő maximális értéket kaptunk, mivel ezen a ponton változik a függvény előjele, és a grafikon csökkenni kezd. Lásd az illusztrációt:

Vagyis y (0) = 1 0 2 - 4 = - 1 4 lesz maximális értékeket funkciókat.

Most határozzuk meg a függvény viselkedését egy x-re, amely a jobb oldalon -2-re, a bal oldalon pedig + 2-re hajlamos. Más szóval, egyoldalú korlátokat találunk:

lim x → - 2 + 0 1 x 2 - 4 = lim x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 · 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = lim x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = - ∞

Kiderült, hogy a függvényértékek mínusz végtelenről -1 4-re nőnek, ha az argumentum -2-ről 0-ra változik. És amikor az argumentum 0-ról 2-re változik, a függvényértékek mínusz végtelen felé csökkennek. Következésképpen egy adott függvény értékkészlete a szükséges intervallumon (- ∞ ; - 1 4 ] lesz.

Válasz: (- ∞ ; - 1 4 ] .

4. példa

Feltétel: adja meg az y = t g x értékek halmazát egy adott intervallumon - π 2; π 2.

Megoldás

Tudjuk, hogy általános esetben az érintő deriváltja - π 2; π 2 pozitív lesz, vagyis a függvény növekedni fog. Most határozzuk meg, hogyan viselkedik a függvény a megadott határokon belül:

lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞

Megkaptuk a függvény értékeinek növekedését mínusz végtelenről plusz végtelenre, amikor az argumentum -π 2-ről π 2-re változik, és azt mondhatjuk, hogy ennek a függvénynek a megoldási halmaza az összes valós szám halmaza lesz. .

Válasz: - ∞ ; + ∞ .

5. példa

Feltétel: határozza meg az y = ln x természetes logaritmusfüggvény tartományát.

Megoldás

Tudjuk, hogy ez a függvény a D (y) = 0 argumentum pozitív értékeire van definiálva; + ∞ . A derivált egy adott intervallumon pozitív lesz: y " = ln x " = 1 x . Ez azt jelenti, hogy a funkció növekszik rajta. Ezután meg kell határoznunk egy egyoldalú határértéket arra az esetre, amikor az argumentum 0-ra hajlik (a jobb oldalon), és amikor x a végtelenbe megy:

lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞

Azt találtuk, hogy a függvény értékei mínusz végtelenről plusz végtelenre nőnek, ahogy x értékei nulláról plusz végtelenre változnak. Ez azt jelenti, hogy az összes valós szám halmaza a természetes logaritmus függvény értéktartománya.

Válasz: az összes valós szám halmaza a természetes logaritmus függvény értéktartománya.

6. példa

Feltétel: határozza meg az y = 9 x 2 + 1 függvény tartományát.

Megoldás

Ez a függvény akkor van definiálva, ha x egy valós szám. Számítsuk ki a függvény legnagyobb és legkisebb értékét, valamint növekedési és csökkenési intervallumait:

y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0

Ennek eredményeként megállapítottuk, hogy ez a függvény csökkenni fog, ha x ≥ 0; növekszik, ha x ≤ 0 ; maximum pontja y (0) = 9 0 2 + 1 = 9 0-val egyenlő változóval.

Nézzük meg, hogyan viselkedik a függvény a végtelenben:

lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = + 0

A rekordból egyértelműen kiderül, hogy a függvényértékek ebben az esetben aszimptotikusan megközelítik a 0-t.

Összefoglalva: amikor az argumentum mínusz végtelenről nullára változik, a függvényértékek 0-ról 9-re nőnek. Ha az argumentumértékek 0-ról plusz végtelenre változnak, a megfelelő függvényértékek 9-ről 0-ra csökkennek. Ezt mutattuk be az ábrán:

Azt mutatja, hogy a függvény értéktartománya az E (y) = (0 ; 9 ] intervallum lesz)

Válasz: E (y) = (0 ; 9 ]

Ha meg kell határoznunk az y = f (x) függvény értékkészletét az [ a ; b) , (a ; b ] , [a ; + ∞) , (- ∞ ; b ] ), akkor pontosan ugyanazokat a vizsgálatokat kell elvégeznünk, ezeket az eseteket egyelőre nem elemezzük, később találkozunk velük. problémákat.

De mi van akkor, ha egy bizonyos függvény definíciós tartománya több intervallum uniója? Ezután ki kell számítanunk az egyes intervallumok értékkészletét, és kombinálnunk kell őket.

7. példa

Feltétel: határozza meg, hogy mekkora lesz az értéktartomány y = x x - 2 .

Megoldás

Mivel a függvény nevezőjét nem szabad 0-ra fordítani, akkor D (y) = - ∞; 2 ∪ 2; + ∞ .

Kezdjük azzal, hogy meghatározzuk a függvényértékek halmazát az első szegmensen - ∞; 2, ami egy nyitott gerenda. Tudjuk, hogy a rajta lévő függvény csökkenni fog, vagyis ennek a függvénynek a deriváltja negatív lesz.

lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0

Ekkor azokban az esetekben, amikor az argumentum mínusz végtelen felé változik, a függvényértékek aszimptotikusan közelednek az 1-hez. Ha x értékei mínusz végtelenről 2-re változnak, akkor az értékek 1-ről mínusz végtelenre csökkennek, azaz. ezen a szegmensen a függvény a - ∞ intervallumból veszi az értékeket; 1 . Az egységet kizárjuk szempontjaink közül, mivel a függvény értékei nem érik el, hanem csak aszimptotikusan közelítenek hozzá.

Nyitott gerendához 2; + ∞ pontosan ugyanazokat a műveleteket hajtjuk végre. A funkció is csökken rajta:

lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0

A függvény értékeit egy adott szegmensen az 1 halmaz határozza meg; + ∞ . Ez azt jelenti, hogy a feltételben megadott függvényhez szükséges értéktartomány a halmazok uniója lesz - ∞ ; 1. és 1.; + ∞ .

Válasz: E (y) = -∞ ; 1 ∪ 1; + ∞ .

Ez látható a grafikonon:

Speciális eset a periodikus függvények. Értéktartományuk egybeesik a funkció periódusának megfelelő intervallum értékkészletével.

8. példa

Feltétel: határozza meg a szinusz y = sin x értéktartományát.

Megoldás

A szinusz periodikus függvény, periódusa 2 pi. Vegyük a 0 szegmenst; 2 π, és nézd meg, mi lesz az értékkészlet rajta.

y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z

0-n belül; 2 π a függvénynek π 2 és x = 3 π 2 szélsőpontjai lesznek. Számítsuk ki, hogy a függvényértékek mennyivel lesznek egyenlők bennük, valamint a szegmens határain, majd válasszuk ki a legnagyobb és legkisebb értéket.

y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1, max x ∈ 0; 2 π sin x = sin π 2 = 1

Válasz: E (sin x) = -1; 1 .

Ha ismernie kell az olyan függvények tartományait, mint a hatvány, az exponenciális, a logaritmikus, a trigonometrikus, az inverz trigonometrikus, akkor javasoljuk, hogy olvassa el újra az alapvető elemi függvényekről szóló cikket. Az itt bemutatott elmélet lehetővé teszi, hogy ellenőrizzük az ott megadott értékeket. Célszerű ezeket megtanulni, mert gyakran szükség van rájuk a problémák megoldása során. Ha ismeri az alapfüggvények tartományait, könnyen megtalálhatja azokat a függvénytartományokat, amelyeket az elemi függvényekből geometriai transzformációval kapunk.

9. példa

Feltétel: határozza meg az y = 3 a r c cos x 3 + 5 π 7 - 4 értéktartományt.

Megoldás

Tudjuk, hogy a 0-tól pi-ig terjedő szakasz az ív koszinusz tartomány. Más szavakkal, E (a r c cos x) = 0; π vagy 0 ≤ a r c cos x ≤ π . Az ív koszinuszból az a r c cos x 3 + 5 π 7 függvényt megkaphatjuk az O x tengely mentén történő eltolással és nyújtással, de az ilyen transzformációk nem adnak semmit. Ez azt jelenti, hogy 0 ≤ a r c cos x 3 + 5 π 7 ≤ π .

A 3 a r c cos x 3 + 5 π 7 függvényt az a r c cos x 3 + 5 π 7 ív koszinuszból kaphatjuk meg az ordináta tengely mentén történő nyújtással, azaz. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . A végső transzformáció az O y tengely mentén 4 értékkel történő eltolódás. Ennek eredményeként kettős egyenlőtlenséget kapunk:

0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 ív x 3 + 5 π 7 - 4 ≤ 3 π - 4

Azt találtuk, hogy a szükséges értéktartomány egyenlő lesz: E (y) = - 4; 3 π - 4 .

Válasz: E(y)=-4; 3 π - 4 .

Magyarázat nélkül írunk még egy példát, mert teljesen hasonló az előzőhöz.

10. példa

Feltétel: Számítsd ki, hogy mekkora lesz az y = 2 2 x - 1 + 3 függvény tartománya!

Megoldás

Írjuk át a feltételben megadott függvényt a következőre: y = 2 · (2 ​​× - 1) - 1 2 + 3. Az y = x - 1 2 hatványfüggvénynél az értéktartomány a 0 intervallumon lesz meghatározva; + ∞, azaz. x - 1 2 > 0 . Ebben az esetben:

2 x - 1 - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 + 3 > 3

Tehát E(y) = 3; + ∞ .

Válasz: E(y)=3; + ∞ .

Most nézzük meg, hogyan találjuk meg egy nem folytonos függvény értéktartományát. Ehhez fel kell osztanunk a teljes területet intervallumokra, és mindegyikben értékkészletet kell találnunk, majd kombinálni kell, amit kapunk. Ennek jobb megértése érdekében javasoljuk, hogy tekintse át a függvénytöréspontok fő típusait.

11. példa

Feltétel: adott a függvény y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3< x ≤ 3 1 x - 3 , x >3. Számítsa ki az értéktartományát!

Megoldás

Ez a függvény az x összes értékéhez definiálva van. Elemezzük a folytonosság szempontjából az argumentum -3 és 3 értékeivel:

lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)

Az első típusú eltávolíthatatlan folytonossági hiányunk van, ha az argumentum értéke -3. Ahogy közelítjük, a függvény értékei hajlamosak -2 sin 3 2 - 4, és ahogy az x a -3-ra hajlik a jobb oldalon, az értékek -1-re.

lim x → 3 - 0 f (x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f (x) = lim x → 3 + 0 1 x - 3 = + ∞

A 3. pontban van egy eltávolíthatatlan, második típusú folytonossági hiányunk. Amikor egy függvény arra törekszik, értékei megközelítik - 1-et, ha ugyanarra a pontra irányulnak a jobb oldalon - a mínusz végtelenhez.

Ez azt jelenti, hogy ennek a függvénynek a teljes definíciós tartománya 3 intervallumra van felosztva (- ∞ ; - 3 ], (- 3 ; 3 ], (3 ; + ∞).

Az elsőben az y = 2 sin x 2 - 4 függvényt kaptuk. Mivel - 1 ≤ sin x ≤ 1, a következőket kapjuk:

1 ≤ sin x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2

Ez azt jelenti, hogy egy adott intervallumon (- ∞ ; - 3 ] a függvényértékek halmaza [ - 6 ; 2 ] .

A félintervallumon (- 3; 3 ] az eredmény egy állandó függvény y = - 1. Következésképpen az értékeinek teljes halmaza ebben az esetben egy számra - 1 -re csökken.

A második intervallumban 3 ; + ∞ van az y = 1 x - 3 függvény. Csökken, mert y " = - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0

Ez azt jelenti, hogy az eredeti függvény értékkészlete x > 3 esetén a 0; + ∞ . Most kombináljuk az eredményeket: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0; + ∞ .

Válasz: E(y)=-6; - 2 ∪ - 1 ∪ 0; + ∞ .

A megoldást a grafikon mutatja:

12. példa

Feltétel: van egy y = x 2 - 3 e x függvény. Határozza meg értékeinek halmazát!

Megoldás

Meg van határozva minden olyan argumentumértékhez, amely valós szám. Határozzuk meg, hogy ez a függvény mely intervallumokban növekszik, és melyikben csökken:

y " = x 2 - 3 e x " = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x

Tudjuk, hogy a derivált 0 lesz, ha x = - 1 és x = 3. Helyezzük ezt a két pontot a tengelyre, és nézzük meg, hogy a derivált milyen előjelekkel rendelkezik a kapott intervallumokon.

A függvény értéke (- ∞ ; - 1 ] ∪ [ 3 ; + ∞ ) csökken, és [ - 1 ; 3]. A minimális pont - 1, a maximum - 3 lesz.

Most keressük meg a megfelelő függvényértékeket:

y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3

Nézzük meg a függvény viselkedését a végtelenben:

lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 " e x " = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x " (e x) " = 2 lim x → + ∞ 1 e x = 2 1 + ∞ = + 0

A második határ kiszámításához a L'Hopital-szabályt használtuk. Ábrázoljuk a megoldásunk menetét grafikonon.

Azt mutatja, hogy a függvényértékek plusz végtelenről -2e-ra csökkennek, ha az argumentum mínusz végtelenről -1-re változik. Ha 3-ról plusz végtelenre változik, akkor az értékek 6 e - 3-ról 0-ra csökkennek, de a 0-t nem éri el.

Így E(y) = [ - 2 e ; + ∞) .

Válasz: E(y) = [-2e; + ∞)

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt

Számos probléma késztet bennünket arra, hogy függvényértékeket keressünk egy bizonyos szegmensben vagy a teljes definíciós tartományban. Ilyen feladatok közé tartozik a kifejezések különféle értékelése és az egyenlőtlenségek megoldása.

Ebben a cikkben meghatározzuk egy függvény értéktartományát, megvizsgáljuk a keresési módszereket, és részletesen elemezzük a példák megoldását az egyszerűtől a bonyolultabbig. Az áttekinthetőség érdekében minden anyagot grafikus illusztrációkkal látunk el. Tehát ez a cikk egy részletes válasz arra a kérdésre, hogy hogyan lehet megtalálni egy függvény tartományát.

Meghatározás.

Az y = f(x) függvény értékkészlete az X intervallumon egy függvény összes értékének halmaza, amelyet az összes iteráció során vesz fel.

Meghatározás.

Függvénytartomány y = f(x) egy függvény összes értékének halmaza, amelyet akkor vesz fel, amikor a definíciós tartományból az összes x-et iterálja.

A függvény tartományát E(f)-ként jelöljük.

Egy függvény tartománya és egy függvény értékkészlete nem ugyanaz. Ezeket a fogalmakat ekvivalensnek tekintjük, ha az y = f(x) függvény értékkészletének megtalálásakor az X intervallum egybeesik a függvény definíciós tartományával.

Ezenkívül ne keverje össze a függvény tartományát az y=f(x) egyenlőség jobb oldalán lévő kifejezés x változójával. Az x változó megengedett értékeinek tartománya az f(x) kifejezéshez az y=f(x) függvény definíciós tartománya.

Az ábrán több példa látható.

A függvények grafikonjait vastag kék vonalak jelzik, a vékony piros vonalak aszimptotákat, a piros pontok és vonalak az Oy tengelyen a megfelelő függvény értéktartományát mutatják.

Mint látható, egy függvény értéktartományát úgy kapjuk meg, hogy a függvény grafikonját az y tengelyre vetítjük. Ez lehet egyetlen szám (első eset), számhalmaz (második eset), szegmens (harmadik eset), intervallum (negyedik eset), nyitott sugár (ötödik eset), unió (hatodik eset) stb. .

Tehát mit kell tennie egy függvény értéktartományának megtalálásához?

Kezdjük a legegyszerűbb esettel: megmutatjuk, hogyan határozzuk meg az y = f(x) folytonos függvény értékkészletét a szakaszon.

Ismeretes, hogy egy intervallumon folytonos függvény eléri rajta a maximális és minimális értéket. Így a szegmensen az eredeti függvény értékkészlete lesz a szegmens . Következésképpen a feladatunk az, hogy megkeressük a függvény legnagyobb és legkisebb értékét a szegmensen.

Például keressük meg az arcszinusz függvény értéktartományát.

Példa.

Adja meg az y = arcsinx függvény tartományát.

Megoldás.

Az arcszinusz definíciós területe a [-1; 1] . Keressük meg a függvény legnagyobb és legkisebb értékét ezen a szegmensen.

A derivált minden x-re pozitív a (-1; 1) intervallumból, vagyis az arcszinusz függvény a teljes definíciós tartományon növekszik. Következésképpen a legkisebb értéket x = -1-nél, a legnagyobbat pedig x = 1-nél veszi fel.

Megkaptuk az arcszinuszfüggvény tartományát .

Példa.

Keresse meg a függvényértékek halmazát a szegmensen.

Megoldás.

Keressük meg a függvény legnagyobb és legkisebb értékét egy adott szakaszon.

Határozzuk meg a szegmenshez tartozó szélsőpontokat:

Kiszámoljuk az eredeti függvény értékeit a szegmens végén és a pontokon :

Ezért egy függvény értékkészlete egy intervallumon az intervallum .

Most megmutatjuk, hogyan találjuk meg az y = f(x) folytonos függvény értékkészletét az (a; b), , intervallumokban.

Először meghatározzuk a függvény szélsőpontjait, szélsőértékeit, a függvény növekedési és csökkenési intervallumait egy adott intervallumon. Ezután kiszámítjuk az intervallum végén és (vagy) a határértékeket a végtelenben (vagyis megvizsgáljuk a függvény viselkedését az intervallum határain vagy a végtelenben). Ez az információ elegendő ahhoz, hogy megtalálja a függvényértékek készletét ilyen intervallumokon.

Példa.

Határozza meg a függvényértékek halmazát a (-2; 2) intervallumon.

Megoldás.

Keressük meg a függvény (-2; 2) intervallumra eső szélsőpontjait:

Pont x = 0 egy maximális pont, mivel a derivált az előjelet pluszból mínuszba változtatja, amikor áthalad rajta, és a függvény grafikonja növekvőről csökkenőre változik.

van egy megfelelő maximuma a függvénynek.

Nézzük meg a függvény viselkedését, amikor x a jobb oldalon -2-re, míg az x a bal oldalon 2-re hajlik, azaz egyoldalú határértékeket találunk:

Amit kaptunk: amikor az argumentum -2-ről nullára változik, a függvényértékek mínusz végtelenről mínusz egynegyedére nőnek (a függvény maximuma x = 0-nál), amikor az argumentum nulláról 2-re változik, a a függvényértékek mínusz végtelenre csökkennek. Így a függvényértékek halmaza a (-2; 2) intervallumon .

Példa.

Adja meg az y = tgx érintőfüggvény értékkészletét az intervallumon.

Megoldás.

Az intervallum érintőfüggvényének deriváltja pozitív , ami a funkció növekedését jelzi. Vizsgáljuk meg a függvény viselkedését az intervallum határain:

Így, amikor az argumentum értékről -re változik, a függvényértékek mínusz végtelenről plusz végtelenre nőnek, vagyis ezen az intervallumon az érintőértékek halmaza az összes valós szám halmaza.

Példa.

Határozzuk meg az y = lnx természetes logaritmusfüggvény tartományát!

Megoldás.

A természetes logaritmus függvény definiálva van pozitív értékeketérv . Ezen az intervallumon a derivált pozitív , ez a rajta lévő funkció növekedését jelzi. Keressük meg a függvény egyoldali határát, mivel az argumentum a jobb oldalon nullára, az x határértéke pedig a végtelenre hajlik:

Látjuk, hogy amikor x nulláról plusz végtelenre változik, a függvény értékei mínusz végtelenről plusz végtelenre nőnek. Ezért a természetes logaritmus függvény tartománya a valós számok teljes halmaza.

Példa.

Megoldás.

Ez a funkció mindenki számára meghatározott valódi értékeket x. Határozzuk meg a függvény szélsőpontjait, valamint növekedési és csökkenési intervallumait.

Következésképpen a függvény csökken -ben, növekszik -nál, x = 0 a maximális pont, a függvény megfelelő maximumát.

Nézzük meg a függvény viselkedését a végtelenben:

Így a végtelenben a függvény értékei aszimptotikusan megközelítik a nullát.

Megállapítottuk, hogy amikor az argumentum mínusz végtelenről nullára (maximális pontra) változik, a függvény értéke nulláról kilencre (a függvény maximumára) nő, és amikor x nulláról plusz végtelenre változik, a függvény az értékek kilencről nullára csökkennek.

Nézd meg a vázlatos rajzot.

Most már jól látható, hogy a függvény értéktartománya .

Hasonló kutatást igényel az y = f(x) függvény értékkészletének intervallumokon való megtalálása. Ezekre az esetekre most nem térünk ki részletesen. Az alábbi példákban újra találkozunk velük.

Legyen az y = f(x) függvény definíciós tartománya több intervallum uniója. Egy ilyen függvény értéktartományának megtalálásakor meg kell határozni az egyes intervallumok értékkészletét, és egyesíteni kell őket.

Példa.

Keresse meg a függvény tartományát.

Megoldás.

Függvényünk nevezője ne menjen nullára, azaz .

Először keressük meg a függvényértékek halmazát a nyílt sugáron.

Függvény származéka negatív ezen az intervallumon, vagyis a függvény csökken rajta.

Azt találtuk, hogy mivel az argumentum a végtelen mínuszára hajlamos, a függvényértékek aszimptotikusan megközelítik az egységet. Amikor x mínusz végtelenről kettőre változik, a függvény értékei egyről mínusz végtelenre csökkennek, vagyis a vizsgált intervallumon a függvény egy értékkészletet vesz fel. Az egységet nem vesszük figyelembe, mivel a függvény értékei nem érik el, hanem csak aszimptotikusan hajlanak hozzá a mínusz végtelenben.

Hasonló módon járunk el a nyitott gerenda esetében is.

Ezen az intervallumon a függvény is csökken.

A függvényértékek halmaza ezen az intervallumon a készlet.

Így a függvény kívánt értéktartománya a és a halmazok uniója.

Grafikus illusztráció.

Különös figyelmet kell fordítani az időszakos funkciókra. A periodikus függvények értéktartománya egybeesik a függvény periódusának megfelelő intervallum értékkészletével.

Példa.

Határozzuk meg az y = sinx szinuszfüggvény tartományát.

Megoldás.

Ez a függvény periodikus, két pi periódussal. Vegyünk egy szegmenst, és határozzuk meg rajta az értékkészletet.

A szegmens két szélsőpontot és .

Kiszámítjuk a függvény értékeit ezeken a pontokon és a szakasz határain, kiválasztjuk a legkisebb és legnagyobb értéket:

Ennélfogva, .

Példa.

Keresse meg egy függvény tartományát .

Megoldás.

Tudjuk, hogy az arc koszinusz tartomány a nullától pi-ig terjedő szakasz, azaz vagy egy másik bejegyzésben. Funkció az arccosx-ból az abszcissza tengelye mentén történő eltolással és nyújtással nyerhető. Az ilyen transzformációk nem befolyásolják az értéktartományt, ezért . Funkció megszerzett valahonnan háromszoros nyújtás az Oy tengely mentén, azaz . Az átalakulás utolsó szakasza pedig négy egységgel lefelé történő eltolódás az ordináta mentén. Ez kétszeres egyenlőtlenséghez vezet

Így a szükséges értéktartomány a .

Adjuk meg egy másik példának a megoldást, de magyarázat nélkül (nem kötelező, mert teljesen hasonlóak).

Példa.

Funkciótartomány meghatározása .

Megoldás.

Írjuk be az eredeti függvényt a formába . A teljesítményfüggvény értéktartománya az intervallum. Azaz,. Akkor

Ennélfogva, .

Hogy teljes legyen a kép, egy olyan függvény értéktartományának megtalálásáról kell beszélnünk, amely nem folytonos a definíciós tartományban. Ebben az esetben a definíciós tartományt töréspontokkal intervallumokra osztjuk, és mindegyiken értékkészleteket keresünk. A kapott értékkészletek kombinálásával megkapjuk az eredeti függvény értéktartományát. Javasoljuk, hogy emlékezzen a bal oldali 3-ra, a függvény értékei mínusz egyre irányulnak, és ahogy az x a 3-ra hajlamos a jobb oldalon, a függvény értékei általában plusz a végtelen.

Így a függvény definíciós tartományát három intervallumra osztjuk.

Az intervallumon megvan a függvény . Azóta

Így az eredeti függvény értékkészlete az intervallumon [-6;2] .

A félintervallumon y = -1 állandó függvényünk van. Vagyis az eredeti függvény értékkészlete az intervallumon egyetlen elemből áll.

A függvény minden érvényes argumentumértékhez definiálva van. Nézzük meg a függvény növekedési és csökkenési intervallumait.

A derivált x=-1 és x=3 esetén eltűnik. Jelöljük ezeket a pontokat a számegyenesen, és határozzuk meg a derivált előjeleit a kapott intervallumokon.

A funkció értéke csökken , növekszik [-1; 3] , x=-1 minimum pont, x=3 maximum pont.

Számítsuk ki a függvény megfelelő minimumát és maximumát:

Ellenőrizzük a függvény viselkedését a végtelenben:

A második határértéket a segítségével számítottuk ki.

Készítsünk sematikus rajzot.

Amikor az argumentum mínusz végtelenről -1-re változik, a függvényértékek plusz végtelenről -2e-re csökkennek, amikor az argumentum -1-ről 3-ra változik, a függvény értékei -2e-ről -2e-re nőnek, amikor az argumentum változik 3-tól plusz végtelenig a függvényértékek nulláról csökkennek, de nem érik el a nullát.

A függvény az egyik legfontosabb matematikai fogalom.

Definíció: Ha egy bizonyos x halmaz minden számához egyetlen y szám tartozik, akkor azt mondják, hogy ezen a halmazon y(x) függvény van definiálva. Ebben az esetben x-et független változónak vagy argumentumnak, y-t pedig függő változónak vagy egy függvény vagy egyszerűen függvény értékének nevezzük.

Az y változóról azt is mondjuk, hogy az x változó függvénye.

Miután az egyezést egy betűvel, például f-vel jelöltük, kényelmesen írható: y=f (x), vagyis az y értéket az x argumentumból kapjuk az f egyezés segítségével. (Olvassa el: y egyenlő az x f-jével.) Az f (x) szimbólum az x-szel egyenlő argumentum értékének megfelelő függvény értékét jelöli.

1. példa Adjuk meg a függvényt az y=2x 2 –6 képlettel. Ekkor felírhatjuk, hogy f(x)=2x 2 –6. Keressük meg a függvény értékeit például 1-gyel egyenlő x értékekre; 2,5;–3; azaz megtaláljuk az f(1), f(2.5), f(–3):

f(1)=2 1 2 –6=–4;
f(2,5)=2 2,5 2 –6=6,5;
f(–3)=2 (–3) 2 –6= 12.

Figyeljük meg, hogy az y=f (x) alak jelölésében f helyett más betűket használunk: g stb.

Definíció: A függvény tartománya az x összes értéke, amelyre a függvény létezik.

Ha egy függvényt egy képlet ad meg, és a definíciós tartománya nincs megadva, akkor a függvény definíciós tartománya az argumentum összes értékéből áll, amelyre a képletnek értelme van.

Más szóval, egy képlet által megadott függvény tartománya az argumentum összes értéke, kivéve azokat, amelyek olyan műveleteket eredményeznek, amelyeket nem tudunk végrehajtani. Tovább Ebben a pillanatban csak két ilyen akciót ismerünk. Nem oszthatunk nullával, és nem vehetjük fel a negatív szám négyzetgyökét.

Definíció: Minden érték, amelyet a függő változó felvesz a függvény tartományából.

Egy valós folyamatot leíró függvény definíciós tartománya az előfordulásának konkrét feltételeitől függ. Például egy vasrúd l hosszának a t fűtési hőmérséklettől való függését a képlet fejezi ki, ahol l 0 a rúd kezdeti hossza, és a lineáris tágulási együttható. Ez a képlet értelmes t bármely értékére. Az l=g(t) függvény definíciós tartománya azonban egy több tíz fokos intervallum, amelyre a lineáris tágulás törvénye érvényes.

Példa.

Adja meg a függvénytartományt y = arcsinx.

Megoldás.

Az arcszinusz definíciós tartománya a szakasz [-1; 1] . Keressük meg a függvény legnagyobb és legkisebb értékét ezen a szegmensen.

A derivált mindenki számára pozitív x az intervallumból (-1; 1) , vagyis az arcszinusz függvény a teljes definíciós tartományon növekszik. Ezért akkor veszi a legkisebb értéket, amikor x = -1, és a legnagyobb at x = 1.

Megkaptuk az arcszinuszfüggvény tartományát .

Keresse meg a függvényértékek halmazát a szegmensen .

Megoldás.

Keressük meg a függvény legnagyobb és legkisebb értékét egy adott szakaszon.

Határozzuk meg a szakaszhoz tartozó szélsőpontokat :

D(f)- azok az értékek, amelyeket az érvelés felvehet, pl. egy függvény tartománya.

E(f)- azokat az értékeket, amelyeket a függvény felvehet, pl. függvényértékek halmaza.

A függvénytartományok megtalálásának módszerei.

szekvenciális értékek keresése összetett érvek funkciók;

becslés/határ módszer;

függvény folytonossági és monotonitási tulajdonságainak felhasználása;

származék használata;

egy függvény legnagyobb és legkisebb értékének felhasználása;

grafikus módszer;

paraméter beviteli mód;

inverz függvény módszer.

Nézzünk meg néhányat közülük.

Származék használata

Általános megközelítés egy f(x) folytonos függvény értékkészletének megtalálása abból áll, hogy megkeressük az f(x) függvény legnagyobb és legkisebb értékét a tartományában (vagy annak bizonyítását, hogy az egyik vagy mindkettő nem létezik).

Abban az esetben, ha meg kell találnia a függvényértékek halmazait a szegmensen:

keressük meg az adott f "(x) függvény deriváltját;

keresse meg az f(x) függvény kritikus pontjait, és válassza ki azokat, amelyek ehhez a szegmenshez tartoznak;

kiszámítja a függvényértékeket a szegmens végén és a kiválasztott kritikus pontokon;

a talált értékek közül válassza ki a legkisebb és legnagyobb értéket;

A függvényértékek halmaza ezek közé az értékek közé tartozik.

Ha egy függvény tartománya az intervallum, akkor ugyanazt a sémát használjuk, de a végén lévő értékek helyett a függvény határait használjuk, mivel az argumentum az intervallum végére irányul. A tól származó határértékek nem szerepelnek az értékkészletben.

Határok/pontszámok módszere

A függvényértékek készletének megtalálásához először keresse meg az argumentumértékek készletét, majd keresse meg a függvényfüggvény megfelelő legkisebb és legnagyobb értékét. Egyenlőtlenségek segítségével határozzuk meg a határokat.

A lényeg, hogy egy folytonos függvényt alulról és felülről becsüljünk meg, és bizonyítsuk, hogy a függvény eléri a becslések alsó és felső határát. Ebben az esetben a függvényértékek készletének egybeesését a becslés alsó határától a felsőig terjedő intervallummal a függvény folytonossága és más értékek hiánya határozza meg.

A folytonos függvény tulajdonságai

Egy másik lehetőség, hogy a függvényt folytonos monotonná alakítjuk, majd az egyenlőtlenségek tulajdonságait felhasználva megbecsüljük az újonnan kapott függvény értékkészletét.

Az összetett függvényargumentumok értékeinek szekvenciális keresése

A köztes függvények értékkészletének szekvenciális keresése alapján, amelyből a függvény összeáll

Alapvető elemi függvények értéktartományai

Funkció	Többféle jelentés
$y = kx+ b$	E(y) = (-∞;+∞)
$y = x^(2n)$	E(y) =
$y = \cos(x)$	E(y) = [-1;1]
$y = (\rm tg)\, x$	E(y) = (-∞;+∞)
$y = (\rm ctg)\, x$	E(y) = (-∞;+∞)
$y = \arcsin(x)$	E(y) = [-π/2; π/2]
$y = \arccos(x)$	E(y) =
$y = (\rm arctan)\, x$	E(y) = (-π/2; π/2)
$y = (\rm arcctg)\, x$	E(y) = (0; π)

Példák

Keresse meg a függvényértékek halmazát:

Származék használata

Megtaláljuk a definíciós tartományt: D(f)=[-3;3], mert $9-x^(2)\geq 0$

Keresse meg a derivált: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$

f"(x) = 0, ha x = 0. f"(x) nem létezik, ha $\sqrt(9-x^(2))=0$, azaz x = ±3 esetén. Három kritikus pontot kapunk: x 1 = –3, x 2 = 0, x 3 = 3, ebből kettő egybeesik a szakasz végével. Számítsuk ki: f(–3) = 0, f(0) = 3, f(3) = 0. Így f(x) legkisebb értéke 0, legnagyobb értéke 3.

Válasz: E(f) = .

NEM használ derivált

Keresse meg a függvény legnagyobb és legkisebb értékét:

$ óta
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , majd:

$f(x)\leq \frac(3)(4)$ minden x-re;

$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ minden x(a $|\cos óta (x)|\leq 1$);

$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;

$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;

Válasz: $\frac(3)(4)$ és $-\frac(3)(2)$

Ha ezt a problémát deriváltokkal oldja meg, akkor le kell győznie azokat az akadályokat, amelyek abból adódnak, hogy az f(x) függvény nem egy szakaszon, hanem a teljes számegyenesen van definiálva.

A határok/becslések módszerével

A szinusz definíciójából az következik, hogy $-1\leq\sin(x)\leq 1$. Ezután a numerikus egyenlőtlenségek tulajdonságait fogjuk használni.

$-4\leq - 4\sin(x)\leq 4$, (a kettős egyenlőtlenség mindhárom részét -4-gyel megszorozva);

$1\leq 5 - 4\sin(x)\leq 9$ (hozzáadva az 5-ös kettős egyenlőtlenség három részéhez);

Mivel ez a függvény a teljes definíciós tartományon folytonos, értékkészlete a legkisebb és a legnagyobb értéke között van a teljes definíciós tartományban, ha van ilyen.

Ebben az esetben a $y = 5 - 4\sin(x)$ függvény értékkészlete a halmaz.

A $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ egyenlőtlenségekből megkapjuk a $$\\ -6\leq y\ becslést leq 6 $ $

x = p és x = 0 esetén a függvény -6 és 6 értéket vesz fel, azaz. eléri a becslés alsó és felső határát. A cos(7x) és cos(x) folytonos függvények lineáris kombinációjaként az y függvény a teljes számegyenesen folytonos, ezért a folytonos függvény tulajdonsága alapján minden értéket felvesz -6-tól 6-ig. , és csak őket, mivel a $- 6\leq y\leq 6$ egyenlőtlenségek miatt más értékei lehetetlenek.

Ezért E(y) = [-6;6].

$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Válasz: E(f) = .

$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

Alakítsuk át a $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ( (\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)(2 )) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac(\) pi) (4)) $$.

A koszinusz definíciójából következik: $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$

Mivel ez a függvény folytonos a teljes definíciós tartományban, értékeinek halmaza a legkisebb és a legnagyobb értéke között helyezkedik el, ha van ilyen, a függvényértékek halmaza $y =\sqrt(2)\cos((x) A +\frac(\pi)(4 )))$ a $[-\sqrt(2);\sqrt(2)]$ halmaz.

$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$

Jelöljük $t = 5 – (3^(x)+1)^(2)$, ahol -∞≤t≤4. Így a probléma a $y = \log_(0,5)(t)$ függvény értékkészletének megtalálására a (-∞;4) sugáron redukálódik. Mivel a $y = \log_(0,5)(t)$ függvény csak t > 0 esetén van definiálva, ezért a sugáron lévő értékkészlete (-∞;4) egybeesik a függvényértékek halmazával a (0;4) intervallumon a sugár (-∞;4) metszéspontja a logaritmikus függvény definíciós tartományával (0;+∞). A (0;4) intervallumon ez a függvény folyamatos és csökkenő. t > 0 esetén +∞, t = 4 esetén pedig -2 értéket vesz fel, tehát E(y) = (-2, +∞).

Egy függvény grafikus ábrázolásán alapuló technikát használunk.

A függvény átalakítása után a következőt kapjuk: y 2 + x 2 = 25, és y ≥ 0, |x| ≤ 5.

Emlékeztetni kell arra, hogy $x^(2)+y^(2)=r^(2)$ az r sugarú kör egyenlete.

Ezen korlátozások mellett ennek az egyenletnek a grafikonja a felső félkör, amelynek középpontja az origóban van, sugara pedig 5. Nyilvánvaló, hogy E(y) = .

Válasz: E(y) = .

Hivatkozások

Az egységes államvizsga-problémák funkcióinak jelentőségének területe, Irina Boriszovna Minyuk

Tippek egy függvény értékkészletének megtalálásához, Belyaeva I., Fedorova S.

A függvényértékek halmazának megkeresése

Hogyan lehet matematikai problémákat megoldani a felvételi vizsgákon, I. I. Melnikov, I. N. Szergejev