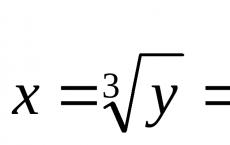Inverz függvény. Elmélet és alkalmazás C 3 inverz függvény 2. opció

Legyen egy y=f(x) függvény, X a definíciós tartománya, Y az értéktartománya. Tudjuk, hogy minden x 0  egyetlen y 0 =f(x 0), y 0 Y értéknek felel meg.

Kiderülhet, hogy minden y (vagy annak  1 része) egy X-ből származó egyetlen x-nek is megfelel.

Ekkor azt mondják, hogy az  régión (vagy annak   részén) az x=y függvény az y=f(x) függvény inverz függvénye.

Például:

x =(); Y=$

Mivel ez a függvény a $X$ intervallumon csökkenő és folytonos, így a $Y=$ intervallumon, amely szintén csökkenő és folytonos ezen az intervallumon (1. tétel).

Számolja ki $x$:

\ \

Válassza ki a megfelelő $x$-t:

Válasz: inverz függvény $y=-\sqrt(x)$.

Problémák az inverz függvények megtalálásakor

Ebben a részben néhány elemi függvény inverz függvényeit fogjuk megvizsgálni. A problémákat a fent megadott séma szerint oldjuk meg.

2. példa

Keresse meg az $y=x+4$ függvény inverz függvényét

Keresse meg a $x$ értéket a $y=x+4$ egyenletből:

3. példa

Keresse meg az $y=x^3$ függvény inverz függvényét

Megoldás.

Mivel a függvény a teljes definíciós tartományon növekvő és folytonos, ezért az 1. Tétel szerint van rajta egy inverz folytonos és növekvő függvény.

Keresse meg az $x$ értéket a $y=x^3$ egyenletből:

$x$ megfelelő értékeinek megtalálása

A mi esetünkben az érték megfelelő (mivel a hatókör minden szám)

A változókat újradefiniálva azt kapjuk, hogy az inverz függvénynek van alakja

4. példa

Keresse meg a $y=cosx$ függvény inverz függvényét a $$ intervallumon

Megoldás.

Tekintsük a $y=cosx$ függvényt a $X=\left$ halmazon. Folyamatos és csökkenő a $X$ halmazon, és leképezi a $X=\left$ halmazt a $Y=[-1,1]$ halmazra, ezért az inverz folytonos monoton függvény létezésére vonatkozó tétel alapján, a $y=cosx$ függvény a $ Y$ halmazban van egy inverz függvény, amely szintén folytonos és növekvő a $Y=[-1,1]$ halmazban és leképezi a $[-1,1]$ halmazt a $\left$ halmazba.

Keresse meg a $x$ értéket a $y=cosx$ egyenletből:

$x$ megfelelő értékeinek megtalálása

A változókat újradefiniálva azt kapjuk, hogy az inverz függvénynek van alakja

5. példa

Keresse meg a $y=tgx$ függvény inverz függvényét a $\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ intervallumban.

Megoldás.

Tekintsük a $y=tgx$ függvényt a $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ halmazon. Folyamatos és növekvő a $X$ halmazon, és leképezi a $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ halmazt a $Y halmazra =R$, ezért az inverz folytonos monoton függvény létezésére vonatkozó tétel szerint a $y=tgx$ függvénynek a $Y$ halmazban van egy inverz függvénye, amely szintén folytonos és növekvő a $Y=R halmazban. $ és leképezi a $R$ halmazt a $\left(- \frac(\pi )(2),\frac(\pi )(2)\right)$ halmazra

Keressük meg az $x$ értéket a $y=tgx$ egyenletből:

$x$ megfelelő értékeinek megtalálása

A változókat újradefiniálva azt kapjuk, hogy az inverz függvénynek van alakja

Találkoztunk már olyan problémával, ahol adott f függvény és argumentuma adott értékénél ezen a ponton kellett kiszámolni a függvény értékét. De néha szembe kell nézni az inverz problémával: egy ismert f függvény és bizonyos y érték mellett meg kell találni annak az argumentumnak az értékét, amelyben a függvény adott y értéket vesz fel.

Azt a függvényt, amely minden értékét a definíciós tartományának egyetlen pontján veszi fel, invertálható függvénynek nevezzük. Például egy lineáris függvény lenne invertálható függvény. De a másodfokú függvény vagy a szinuszfüggvény nem lesz invertálható függvény. Mivel egy függvény ugyanazt az értéket veheti fel különböző argumentumokkal.

Inverz függvény

Tegyük fel, hogy f egy tetszőleges invertálható függvény. Az y0 értéktartományból származó minden szám csak egy számnak felel meg az x0 definíciós tartományból, így f(x0) = y0.

Ha most minden x0 értéket társítunk egy y0 értékkel, akkor új függvényt kapunk. Például egy f(x) = k * x + b lineáris függvény esetén a g(x) = (x - b)/k függvény az inverze.

Ha valamilyen funkciót g minden ponton x az f invertálható függvény értéktartománya olyan értéket vesz fel, hogy f(y) = x, akkor azt mondjuk, hogy a függvény g- van egy inverz függvénye f-nek.

Ha valamilyen f invertálható függvény gráfját adjuk meg, akkor az inverz függvény gráfjának elkészítéséhez a következő állítást használhatjuk: az f függvény gráfja és a g inverz függvénye szimmetrikus lesz az egyeneshez képest. az y = x egyenlettel meghatározott egyenes.

Ha egy g függvény egy f függvény inverze, akkor a g függvény invertálható függvény lesz. Az f függvény pedig a g függvény inverze lesz. Általában azt mondják, hogy két f és g függvény kölcsönösen inverz egymással.

A következő ábra az f és g függvények grafikonjait mutatja, amelyek egymással kölcsönösen inverzek.

Levezetjük a következő tételt: ha egy f függvény valamely A intervallumon növekszik (vagy csökken), akkor invertálható. Az f függvény értéktartományában definiált g inverz függvény is egy növekvő (vagy ennek megfelelően csökkenő) függvény. Ezt a tételt ún inverz függvénytétel.