itthon Internet

A megadott inverz mátrixa és számítási algoritmusa. Keresse meg az inverz mátrixot online

Kezdeti a képlet szerint: A^-1 = A*/detA, ahol A* a társított mátrix, detA az eredeti mátrix. A csatolt mátrix az eredeti mátrix elemeihez való kiegészítések transzponált mátrixa.

Először is keresse meg a mátrix determinánsát, annak nullától eltérőnek kell lennie, mivel akkor a determináns osztóként lesz használva. Adjuk meg például a harmadik mátrixát (három sorból és három oszlopból áll). Mint látható, a mátrix determinánsa nem egyenlő nullával, tehát van egy inverz mátrix.

Keresse meg az A mátrix egyes elemeinek komplementerét. Az A komplementere az i-edik sor és a j-edik oszlop törlésével kapott részmátrix determinánsa, és ezt a determinánst előjellel vesszük. Az előjelet úgy határozzuk meg, hogy a determinánst (-1) megszorozzuk i+j hatványával. Így például az A komplementere lesz a determináns az ábrán. A jel így alakult: (-1)^(2+1) = -1.

Ennek eredményeként kapsz mátrix kiegészítéseket, most ültesse át. A transzpozíció olyan művelet, amely szimmetrikus a mátrix főátlójával, az oszlopok és a sorok felcserélődnek. Így megtalálta a kapcsolódó A* mátrixot.

Ez a téma az egyik leggyűlöltebb a diákok körében. Ami még rosszabb, valószínűleg csak a meghatározók.

A trükk az, hogy maga az inverz elem fogalma (és most nem csak a mátrixokról beszélek) a szorzás műveletére utal. Az iskolai tantervben is összetett műveletnek számít a szorzás, a mátrixszorzás pedig általában külön téma, aminek egy egész bekezdést és egy videóórát szentelek.

Ma nem megyünk bele a mátrixszámítások részleteibe. Ne feledje: hogyan jelöljük a mátrixokat, hogyan szorozzuk őket, és mi következik ebből.

Áttekintés: Mátrixszorzás

Először is állapodjunk meg a jelölésben. A $\left[ m\times n \right]$ méretű $A$ mátrix egyszerűen egy számtáblázat pontosan $m$ sorral és $n$ oszloppal:

\=\zárójel(\left[ \begin(mátrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(mátrix) \jobbra])_(n)\]

Hogy véletlenül ne keverjük össze helyenként a sorokat és az oszlopokat (hidd el, a vizsgán össze lehet keverni egyet a kettessel - mit is mondhatnánk ott néhány sorról), csak vessünk egy pillantást a képre:

Mátrixsejtek indexeinek meghatározása

Mi történik? Ha az $OXY$ szabványos koordinátarendszert a bal felső sarokba helyezzük, és a tengelyeket úgy irányítjuk, hogy azok lefedjék a teljes mátrixot, akkor ennek a mátrixnak minden cellája egyedileg társítható a $\left(x;y \right) koordinátákkal. $ - ez lesz a sorszám és az oszlop száma.

Miért van a koordinátarendszer pontosan a bal felső sarokban? Igen, mert onnan kezdünk el olvasni bármilyen szöveget. Nagyon könnyű megjegyezni.

Miért mutat a $x$ tengely lefelé, és miért nem jobbra? Megint egyszerű: vegyük a szabványos koordinátarendszert (az $x$ tengely jobbra, a $y$ tengely felfelé megy), és forgassa el úgy, hogy az bezárja a mátrixot. Ez egy 90 fokos elforgatás az óramutató járásával megegyező irányban – ennek eredményét látjuk a képen.

Általában kitaláltuk, hogyan határozzuk meg a mátrixelemek indexeit. Most foglalkozzunk a szorzással.

Meghatározás. A $A=\left[ m\times n \right]$ és a $B=\left[ n\times k \right]$ mátrixok, amikor az első oszlopok száma megegyezik a második sorainak számával következetesnek nevezik.

Ebben a sorrendben. Lehet kétértelmű, és azt mondhatjuk, hogy a $A$ és $B$ mátrixok egy $\left(A;B \right)$ rendezett párt alkotnak: ha konzisztensek ebben a sorrendben, akkor egyáltalán nem szükséges, hogy $B $ és $A$, azok. a $\left(B;A \right)$ pár is konzisztens.

Csak konzisztens mátrixok szorozhatók.

Meghatározás. A $A=\left[ m\times n \right]$ és a $B=\left[ n\times k \right]$ konzisztens mátrixok szorzata az új $C=\left[ m\times k \right mátrix ]$ , melynek $((c)_(ij))$ elemeit a következő képlet számítja ki:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Más szavakkal: ahhoz, hogy megkapjuk a $C=A\cdot B$ mátrix $((c)_(ij))$ elemét, az első mátrix $i$-sorát kell venni, a $j$ a második mátrix -edik oszlopát, majd szorozzuk meg párban az ebből a sorból és oszlopból származó elemeket. Adja össze az eredményeket.

Igen, ez kemény meghatározás. Ebből azonnal több tény is következik:

A mátrixszorzás általánosságban véve nem kommutatív: $A\cdot B\ne B\cdot A$;
A szorzás azonban asszociatív: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
És még disztributív: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
És ismét disztributív: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

A szorzás eloszlását külön kellett leírni a bal és a jobb oldali szorzóösszegre, már csak a szorzási művelet nem kommutativitása miatt is.

Ha ennek ellenére kiderül, hogy $A\cdot B=B\cdot A$, az ilyen mátrixokat permutálhatónak nevezzük.

Az összes mátrix között, amelyek megszorozódnak valamivel, vannak speciálisak – azok, amelyek bármely $A$ mátrixszal megszorozva ismét $A$-t adnak:

Meghatározás. A $E$ mátrixot azonosságnak nevezzük, ha $A\cdot E=A$ vagy $E\cdot A=A$. $A$ négyzetmátrix esetén ezt írhatjuk:

Az identitásmátrix gyakori vendég a mátrixegyenletek megoldásában. És általában gyakori vendég a mátrixok világában. :)

És emiatt a $E$ miatt valaki kitalálta a következő játékot.

Mi az inverz mátrix

Mivel a mátrixszorzás nagyon időigényes művelet (egy csomó sort és oszlopot meg kell szorozni), az inverz mátrix fogalma sem a legtriviálisabb. És ehhez némi magyarázat kell.

Kulcs definíció

Nos, ideje megtudni az igazságot.

Meghatározás. A $B$ mátrixot a $A$ mátrix inverzének nevezzük, ha

Az inverz mátrixot $((A)^(-1))$ jelöli (nem tévesztendő össze a fokozattal!), így a definíció így átírható:

Úgy tűnik, hogy minden rendkívül egyszerű és világos. De egy ilyen meghatározás elemzésekor számos kérdés azonnal felmerül:

Mindig létezik inverz mátrix? És ha nem mindig, akkor hogyan lehet meghatározni: mikor létezik és mikor nem?
És ki mondta, hogy egy ilyen mátrix pontosan egy? Mi van akkor, ha valami eredeti $A$ mátrixhoz inverzek egész tömege van?
Hogy néznek ki ezek a "fordítások"? És valójában hogyan számolod meg őket?

Ami a számítási algoritmusokat illeti - erről egy kicsit később fogunk beszélni. De a többi kérdésre most válaszolunk. Rendezzük őket külön állítások-lemmák formájában.

Alaptulajdonságok

Kezdjük azzal, hogyan kell kinéznie a $A$ mátrixnak, hogy $((A)^(-1))$ legyen. Most megbizonyosodunk arról, hogy mindkét mátrixnak négyzet alakúnak és azonos méretűnek kell lennie: $\left[ n\times n \right]$.

1. lemma. Adott egy $A$ mátrix és annak inverze $((A)^(-1))$. Ekkor mindkét mátrix négyzet alakú, és azonos sorrendű $n$.

Bizonyíték. Minden egyszerű. Legyen a $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$ mátrix. Mivel a $A\cdot ((A)^(-1))=E$ szorzat definíció szerint létezik, a $A$ és $((A)^(-1))$ mátrixok következetesek ebben a sorrendben:

\[\begin(igazítás) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( igazítsa)\]

Ez egyenes következménye a mátrixszorzó algoritmusnak: az $n$ és $a$ együtthatók "tranzit" és egyenlőnek kell lenniük.

Ugyanakkor az inverz szorzás is definiálva van: $((A)^(-1))\cdot A=E$, így a $((A)^(-1))$ és $A$ mátrixok következetes is ebben a sorrendben:

\[\begin(igazítás) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( igazítsa)\]

Így az általánosság elvesztése nélkül feltételezhetjük, hogy $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. A $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$ definíciója szerint azonban a mátrixok méretei pontosan megegyeznek:

\[\begin(igazítás) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(igazítás)\]

Így kiderül, hogy mindhárom mátrix - $A$, $((A)^(-1))$ és $E$ - négyzet alakú $\left[ n\times n \right]$. A lemma bevált.

Hát ez már jó. Látjuk, hogy csak a négyzetmátrixok invertálhatók. Most győződjünk meg arról, hogy az inverz mátrix mindig ugyanaz.

2. lemma. Adott egy $A$ mátrix és annak inverze $((A)^(-1))$. Akkor ez az inverz mátrix egyedi.

Bizonyíték. Kezdjük az ellenkezőjével: legyen az $A$ mátrixnak legalább két inverze - $B$ és $C$. Ekkor a definíció szerint a következő egyenlőségek igazak:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(igazítás)\]

Az 1. lemmából arra a következtetésre jutunk, hogy mind a négy $A$, $B$, $C$ és $E$ mátrix azonos sorrendű négyzet: $\left[ n\times n \right]$. Ezért a termék meghatározása:

Mivel a mátrixszorzás asszociatív (de nem kommutatív!), ezt írhatjuk:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Jobbra B=C. \\ \end(igazítás)\]

Az egyetlen lehetséges opciót kaptuk: az inverz mátrix két másolata egyenlő. A lemma bevált.

A fenti érvelés szinte szó szerint megismétli az inverz elem egyediségének bizonyítását minden $b\ne 0$ valós számra. Az egyetlen jelentős kiegészítés a mátrixok dimenziójának figyelembevétele.

Azonban még mindig nem tudunk semmit arról, hogy bármelyik négyzetmátrix megfordítható-e. Itt a determináns jön a segítségünkre – ez minden négyzetmátrix kulcsjellemzője.

3. lemma. Adott egy $A$ mátrix. Ha létezik vele fordított $((A)^(-1))$ mátrix, akkor az eredeti mátrix determinánsa nem nulla:

\[\bal| A \right|\ne 0\]

Bizonyíték. Azt már tudjuk, hogy a $A$ és a $((A)^(-1))$ $\left[ n\times n \right]$ méretű négyzetmátrixok. Ezért mindegyikre ki lehet számítani a determinánst: $\left| A \right|$ és $\left| ((A)^(-1)) \jobbra|$. A szorzat determinánsa azonban egyenlő a determinánsok szorzatával:

\[\bal| A\cdot B \right|=\left| A \right|\cdot \left| B \jobbra|\Jobbra \balra| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \jobbra|\]

De a $A\cdot ((A)^(-1))=E$ definíciója szerint, és a $E$ determinánsa mindig egyenlő 1-gyel, tehát

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E\jobbra|; \\ & \left| A \right|\cdot \left| ((A)^(-1)) \jobbra|=1. \\ \end(igazítás)\]

Két szám szorzata csak akkor egyenlő eggyel, ha mindegyik szám különbözik nullától:

\[\bal| A \right|\ne 0;\quad \left| ((A)^(-1)) \jobbra|\ne 0.\]

Így kiderül, hogy $\left| A \right|\ne 0$. A lemma bevált.

Valójában ez a követelmény teljesen logikus. Most elemezzük az inverz mátrix megtalálásának algoritmusát - és teljesen világossá válik, hogy elvileg miért nem létezhet inverz mátrix nulla determinánssal.

De először fogalmazzunk meg egy "kiegészítő" definíciót:

Meghatározás. A degenerált mátrix egy $\left[ n\x n \right]$ méretű négyzetmátrix, amelynek determinánsa nulla.

Így kijelenthetjük, hogy bármely invertálható mátrix nem degenerált.

Hogyan találjuk meg az inverz mátrixot

Most megvizsgálunk egy univerzális algoritmust az inverz mátrixok megtalálására. Általában két általánosan elfogadott algoritmus létezik, és ma a másodikkal is foglalkozunk.

A most figyelembe vett mátrix nagyon hatékony a $\left[ 2\x 2 \right]$ és - részben - a $\left[ 3\x 3 \right]$ méretű mátrixok esetén. De a $\left[ 4\x 4 \right]$ mérettől kezdve jobb, ha nem használod. Miért – most mindent meg fog érteni.

Algebrai összeadások

Készülj fel. Most fájdalom lesz. Nem, ne aggódj: egy gyönyörű nővér szoknyában, csipkés harisnyában nem jön be, és nem ad be injekciót a fenékbe. Minden sokkal prózaibb: az algebrai kiegészítések és Őfelsége, az „Union Matrix” jönnek Önhöz.

Kezdjük a fővel. Legyen egy $A=\left[ n\times n \right]$ méretű négyzetmátrix, melynek elemei a $((a)_(ij))$ nevet kapják. Ezután minden ilyen elemhez definiálhatunk egy algebrai komplementet:

Meghatározás. A $((A)_(ij))$ algebrai komplementer a $((a)_(ij))$ elemhez a $i$-edik sorában és a $j$-edik oszlopában a $A=\left mátrixban Az [ n \times n \right]$ az űrlap konstrukciója

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Ahol $M_(ij)^(*)$ az eredeti $A$-ból ugyanazon $i$-edik sor és $j$-edik oszlop törlésével kapott mátrix determinánsa.

Újra. A $\left(i;j \right)$ koordinátákkal rendelkező mátrixelem algebrai kiegészítését $((A)_(ij))$-ként jelöljük, és a következő séma szerint számítjuk ki:

Először töröljük az eredeti mátrixból a $i$-sort és a $j$-edik oszlopot. Kapunk egy új négyzetmátrixot, és a determinánsát $M_(ij)^(*)$-ként jelöljük.
Ezután ezt a determinánst megszorozzuk $((\left(-1 \right))^(i+j))$-val - elsőre ez a kifejezés észbontónak tűnhet, de valójában csak megtudjuk a $ előtti jelet M_(ij)^(*) $.
Számolunk - egy adott számot kapunk. Azok. az algebrai összeadás csak egy szám, nem valami új mátrix stb.

Magát a $M_(ij)^(*)$ mátrixot a $((a)_(ij))$ elem komplementer minorjának nevezzük. És ebben az értelemben az algebrai komplementer fenti definíciója egy összetettebb definíció speciális esete - annak, amelyet a determinánsról szóló leckében megvizsgáltunk.

Fontos jegyzet. Valójában a "felnőtt" matematikában az algebrai összeadások meghatározása a következő:

Négyzetmátrixban $k$ sorokat és $k$ oszlopokat veszünk. A metszéspontjuknál egy $\left[ k\x k \right]$ méretű mátrixot kapunk – determinánsát $k$ rendű minornak nevezzük, és $((M)_(k))$-val jelöljük.

Ezután áthúzzuk ezeket a "kiválasztott" $k$ sorokat és $k$ oszlopokat. Ismét kapunk egy négyzetes mátrixot - a determinánsát komplementer minornak nevezzük, és $M_(k)^(*)$-val jelöljük.

Szorozzuk meg $M_(k)^(*)$ értékét $((\left(-1 \right))^(t))$-val, ahol $t$ (figyelem!) az összes kijelölt sor számának összege és oszlopok . Ez lesz az algebrai összeadás.

Vessen egy pillantást a harmadik lépésre: valójában 2 000 dolláros kifejezések összege van! A másik dolog, hogy $k=1$-ra csak 2 tagot kapunk - ezek ugyanazok lesznek a $i+j$ - a $((a)_(ij))$ elem "koordinátái", amelyre mi algebrai kiegészítést keres.

Tehát ma egy kissé leegyszerűsített definíciót használunk. De mint később látni fogjuk, ez bőven elég lesz. Sokkal fontosabb a következő:

Meghatározás. A $S$ uniómátrix a $A=\left[ n\times n \right]$ négyzetmátrixhoz egy új $\left[ n\times n \right]$ méretű mátrix, amelyet $A$-ból kapunk. a $(( a)_(ij))$ helyére a $((A)_(ij))$ algebrai kiegészítőkkel:

\\Jobbra S=\left[ \begin(mátrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(mátrix) \jobbra]\]

Az első gondolat, ami a definíció felismerésének pillanatában felmerül: „ennyit kell összesen számolni!” Nyugi: számolni kell, de nem annyira. :)

Nos, ez mind nagyon szép, de miért van erre szükség? De miért.

Főtétel

Menjünk vissza egy kicsit. Ne feledje, a 3. lemma kimondta, hogy egy $A$ invertálható mátrix mindig nem szinguláris (vagyis a determinánsa nem nulla: $\left| A \right|\ne 0$).

Tehát fordítva is igaz: ha az $A$ mátrix nem degenerált, akkor mindig invertálható. És van még egy keresési séma is $((A)^(-1))$. Nézd meg:

Inverz mátrix tétel. Legyen adott egy $A=\left[ n\times n \right]$ négyzetmátrix, amelynek determinánsa nem nulla: $\left| A \right|\ne 0$. Ekkor létezik a $((A)^(-1))$ inverz mátrix, és a következő képlettel számítjuk ki:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

És most - mindegy, de jól olvasható kézírással. Az inverz mátrix megtalálásához a következőkre lesz szüksége:

Számítsa ki a $\left| determinánst Egy \right|$, és győződjön meg arról, hogy nem nulla.
Állítsd össze a $S$ uniómátrixot, azaz! számoljon meg 100500 algebrai összeadást $((A)_(ij))$, és tegye a helyére $((a)_(ij))$.
Transzponálja ezt a $S$ mátrixot, majd szorozza meg valamilyen $q=(1)/(\left| A \right|)\;$ számmal.

És ez az! Megtalálható a $((A)^(-1))$ inverz mátrix. Nézzünk példákat:

\[\left[ \begin(mátrix) 3 & 1 \\ 5 & 2 \\\end(mátrix) \right]\]

Megoldás. Ellenőrizzük a megfordíthatóságot. Számítsuk ki a determinánst:

\[\bal| A \right|=\left| \begin(mátrix) 3 & 1 \\ 5 & 2 \\\end(mátrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

A determináns különbözik a nullától. Tehát a mátrix megfordítható. Hozzunk létre egy szakszervezeti mátrixot:

Számítsuk ki az algebrai összeadásokat:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\jobbra|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\jobbra|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \jobbra|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\jobbra|=3. \\ \end(igazítás)\]

Figyeld: |2|, |5|, |1| meghatározó tényezők és |3| a $\left[ 1\x 1 \right]$ méretű mátrixok meghatározói, nem pedig a modulok. Azok. ha negatív számok voltak a determinánsokban, akkor nem szükséges eltávolítani a "mínuszt".

Összességében a szakszervezeti mátrixunk így néz ki:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (tömb)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(tömb) \jobbra]\]

Rendben, most mindennek vége. Probléma megoldódott.

Válasz. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Feladat. Keresse meg az inverz mátrixot:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

Megoldás. Ismét figyelembe vesszük a meghatározót:

\[\begin(align) & \left| \begin(tömb)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(tömb) \right|=\begin(mátrix ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\bal (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(mátrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

A determináns különbözik a nullától - a mátrix invertálható. De most ez lesz a legapróbb: 9 (kilenc, a fenébe!) algebrai összeadást is meg kell számolni. És mindegyik tartalmazza a $\left[ 2\times 2 \right]$ minősítőt. Repült:

\[\begin(mátrix) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(mátrix) 2 & -1 \\ 0 & 1 \\\end(mátrix) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(mátrix) 0 & -1 \\ 1 & 1 \\\end(mátrix) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(mátrix) 0 & 2 \\ 1 & 0 \\\end(mátrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(mátrix) 1 & -1 \\ 0 & 2 \\\end(mátrix) \right|=2; \\ \end(mátrix)\]

Röviden, a szakszervezeti mátrix így fog kinézni:

Ezért az inverz mátrix a következő lesz:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(mátrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(mátrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(array) \right]\]

Nos, ez minden. Itt a válasz.

Válasz. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

Mint látható, minden példa végén ellenőrzést végeztünk. Ezzel kapcsolatban egy fontos megjegyzés:

Ne légy lusta ellenőrizni. Szorozzuk meg az eredeti mátrixot a talált inverzsel - $E$-t kell kapnia.

Sokkal egyszerűbb és gyorsabb elvégezni ezt az ellenőrzést, mint hibát keresni a további számításoknál, amikor például egy mátrixegyenletet old meg.

Alternatív mód

Mint mondtam, az inverz mátrixtétel jól működik a $\left[ 2\x 2 \right]$ és a $\left[ 3\x 3 \right]$ méreteknél (az utóbbi esetben már nem olyan "szép" ). ”), de nagy mátrixok esetén a szomorúság kezdődik.

De ne aggódj: van egy alternatív algoritmus, amivel nyugodtan meg lehet találni az inverzt még a $\left[ 10\x 10 \right]$ mátrix esetében is. De, ahogy ez gyakran lenni szokott, ennek az algoritmusnak a figyelembevételéhez szükségünk van egy kis elméleti háttérre.

Elemi átalakulások

A mátrix különféle transzformációi között több speciális is van - ezeket eleminek nevezik. Pontosan három ilyen átalakulás létezik:

Szorzás. Kiveheti a $i$-edik sort (oszlopot), és megszorozhatja tetszőleges számmal $k\ne 0$;
Kiegészítés. Adjunk hozzá a $i$-edik sorhoz (oszlophoz) bármely másik $j$-edik sort (oszlopot) megszorozva tetszőleges $k\ne 0$ számmal (természetesen $k=0$ is lehetséges, de mi értelme Ennek ellenére semmi sem fog változni).
Permutáció. Vegyük az $i$-edik és a $j$-edik sort (oszlopot), és cseréljük fel őket.

Miért nevezik ezeket a transzformációkat eleminek (nagy mátrixoknál nem tűnnek olyan eleminek), és miért csak három van belőlük - ezek a kérdések túlmutatnak a mai lecke keretein. Ezért nem megyünk bele a részletekbe.

Egy másik fontos dolog: mindezeket a perverziókat a kapcsolódó mátrixon kell végrehajtanunk. Igen, igen, jól hallottad. Most lesz még egy meghatározás – a mai leckében az utolsó.

Csatolt Mátrix

Bizonyára az iskolában egyenletrendszereket oldottatok meg az összeadás módszerével. Nos, vonjon ki egy másikat egy sorból, szorozzon meg egy sort egy számmal - ez minden.

Tehát: most minden a régiben lesz, de már „felnőtt módon”. Kész?

Meghatározás. Legyen megadva a $A=\left[ n\times n \right]$ mátrix és az azonos méretű $n$ $E$ azonosságmátrix. Ezután a kapcsolódó mátrix $\left[ A\left| E\jobbra. A \right]$ egy új $\left[ n\times 2n \right]$ mátrix, amely így néz ki:

\[\left[ A\left| E\jobbra. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(tömb) \jobbra]\]

Röviden: vesszük a $A$ mátrixot, jobb oldalon hozzárendeljük a kívánt méretű $E$ identitásmátrixot, a szépség kedvéért függőleges sávval választjuk el őket - itt a mellékelt. :)

Mi a fogás? És itt van:

Tétel. Legyen az $A$ mátrix invertálható. Tekintsük a $\left[ A\left| adjungált mátrixot E\jobbra. \jobbra]$. Ha használ elemi karakterlánc transzformációk hozza a $\left[ E\left| alakba Fényes. \right]$, azaz a sorok szorzásával, kivonásával és átrendezésével $A$-ból megkapjuk a jobb oldali $E$ mátrixot, majd a bal oldalon kapott $B$ mátrix a $A$ inverze:

\[\left[ A\left| E\jobbra. \jobbra]\balra[ E\left| Fényes. \right]\Rightarrow B=((A)^(-1))\]

Ez ennyire egyszerű! Röviden, az inverz mátrix megtalálásának algoritmusa így néz ki:

Írja be a hozzá tartozó $\left[ A\left| mátrixot E\jobbra. \jobbra]$;
Végezzen elemi karakterlánc-konverziókat, amíg a jobb oldal nem jelenik meg a $A$ helyett: $E$;
Természetesen a bal oldalon is megjelenik valami - egy bizonyos $B$ mátrix. Ez fordítva lesz;
NYERESÉG! :)

Természetesen sokkal könnyebb mondani, mint megtenni. Lássunk tehát néhány példát: a $\left[ 3\x 3 \right]$ és a $\left[ 4\x 4 \right]$ méretekhez.

Feladat. Keresse meg az inverz mátrixot:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Megoldás. Összeállítjuk a mellékelt mátrixot:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 és 1 \\\end(tömb) \jobbra]\]

Mivel az eredeti mátrix utolsó oszlopa egyesekkel van kitöltve, vonja ki az első sort a többiből:

\[\begin(igazítás) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(tömb) \jobbra]\begin(mátrix) \downarrow \\ -1 \\ -1 \\\end(mátrix)\to \\ & \to \balra [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(tömb) \jobbra] \\ \end(igazítás)\]

Nincs több egység, kivéve az első sort. De nem nyúlunk hozzá, különben az újonnan eltávolított egységek elkezdenek "szaporodni" a harmadik oszlopban.

De a második sort kétszer is kivonhatjuk az utolsóból - a bal alsó sarokban egy mértékegységet kapunk:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right]\begin(mátrix) \ \\ \downarrow \\ -2 \\\end(mátrix)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(tömb) \jobbra] \\ \end(igazítás)\]

Most kivonhatjuk az utolsó sort az elsőből és kétszer a másodikból - így „nullázzuk” az első oszlopot:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(tömb) \jobbra]\begin(mátrix) -1 \\ -2 \\ \uparrow \\\end(mátrix)\to \\ & \ \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(igazítás)\]

Szorozzuk meg a második sort -1-gyel, majd vonjuk ki 6-szor az elsőből, és adjunk 1-szer az utolsóhoz:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(mátrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end(mátrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(tömb) \jobbra]\begin(mátrix) -6 \\ \felfelé nyíl \\ +1 \\\end (mátrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(array) \right] \\ \end(igazítás)\]

Csak az 1. és 3. sort kell felcserélni:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(array) \right]\]

Kész! A jobb oldalon található a szükséges inverz mátrix.

Válasz. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Feladat. Keresse meg az inverz mátrixot:

\[\left[ \begin(mátrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(mátrix) \jobbra]\]

Megoldás. Ismét összeállítjuk a mellékeltet:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Kérjünk kölcsön egy kicsit, törődjünk azzal, hogy mennyit kell most számolnunk... és kezdjünk el számolni. Kezdetben „nullázzuk” az első oszlopot úgy, hogy kivonjuk az 1. sort a 2. és 3. sorból:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(tömb) \jobbra]\begin(mátrix) \downarrow \\ -1 \\ -1 \\ \ \\\end(mátrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(igazítás)\]

Túl sok "mínuszt" figyelünk meg a 2-4. Szorozzuk meg mindhárom sort -1-gyel, majd égessük ki a harmadik oszlopot úgy, hogy a 3. sort kivonjuk a többiből:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \right]\begin(mátrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\\end(mátrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (tömb) \jobbra]\begin(mátrix) -2 \\ -1 \\ \felfelé nyíl \\ -2 \\\end(mátrix)\to \\ & \to \left[ \begin(tömb)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(igazítás)\]

Itt az ideje, hogy "sütjük" az eredeti mátrix utolsó oszlopát: vonjuk ki a 4. sort a többiből:

\[\begin(igazítás) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(tömb ) \jobbra]\begin(mátrix) +1 \\ -3 \\ -2 \\ \uparrow \\\end(mátrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(igazítás)\]

Utolsó dobás: "égesse ki" a második oszlopot úgy, hogy kivonja a 2. sort az 1. és 3. sorból:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( tömb) \jobbra]\begin(mátrix) 6 \\ \felfelé nyíl \\ -5 \\ \ \\\end(mátrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(igazítás)\]

És megint az identitásmátrix a bal oldalon, tehát az inverz a jobb oldalon. :)

Válasz. $\left[ \begin(mátrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(mátrix) \right]$

Rendben, most mindennek vége. Ellenőrizd magad – ki vagyok törve. :)

ALGEBRAI KIEGÉSZÍTÉSEK ÉS KISOROK

Legyen egy harmadrendű determináns: .

Kisebb ennek az elemnek felel meg aij harmadrendű determináns az adottból annak a sornak és oszlopnak a törlésével kapott másodrendű determináns, amelynek metszéspontjában az adott elem áll, azaz. én-edik sor és j-adik oszlop. Adott elemnek megfelelő minorok aij fogjuk jelölni M ij.

Például, kisebb M12 elemnek megfelelő egy 12, lesz meghatározó 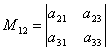, amelyet az 1. sor és a 2. oszlop törlésével kapunk az adott determinánsból.

Így a harmadrendű determinánst meghatározó formula azt mutatja, hogy ez a determináns egyenlő az 1. sor elemei és a hozzájuk tartozó mellékelemek szorzatának összegével; míg az elemnek megfelelő moll egy 12, a „–” jellel veszik, azaz. ezt lehet írni

(1)

Hasonlóképpen bevezethetjük a kiskorúak definícióit a másodrendű és magasabb rendű determinánsok számára.

Mutassunk be még egy fogalmat.

Algebrai összeadás elem aij determinánst minornak nevezzük M ij szorozva (–1) i+j .

Algebrai elemösszeadás aij jelöljük A ij.

A definícióból azt kapjuk, hogy egy elem algebrai komplementere és mollja közötti kapcsolatot az egyenlőség fejezi ki. A ij= (–1) i+j M ij .

Például,

Példa. Adott egy meghatározó. megtalálja A 13, A 21, A 32.

Könnyen belátható, hogy az elemek algebrai összeadásával az (1) képlet a következőképpen írható fel:

Ehhez a képlethez hasonlóan megkaphatjuk a determináns dekompozícióját bármely sor vagy oszlop elemeire.

Például a determináns bontása a 2. sor elemei között a következőképpen érhető el. A determináns 2. tulajdonsága szerint a következőkkel rendelkezünk:

Bővítsük ki a kapott determinánst az 1. sor elemeivel.

(2)

Innen mert a (2) képlet másodrendű determinánsai az elemek minorjai 21, 22, 23. Így , azaz. megkaptuk a determináns kiterjesztését a 2. sor elemeivel.

Hasonlóképpen megkaphatjuk a determináns bontását a harmadik sor elemeire. A determinánsok 1. tulajdonságának felhasználásával (transzpozíciónál) kimutatható, hogy hasonló kiterjesztések érvényesek az oszlopelemek bővítésére is.

Így igaz a következő tétel.

Tétel (egy adott sorban vagy oszlopban a determináns bővítéséről). A determináns egyenlő bármely sora (vagy oszlopa) elemeinek és algebrai komplementereinek szorzatával.

A fentiek mindegyike igaz bármely magasabb rendű determinánsra.

Példák.

INVERZ MÁTRIX

Az inverz mátrix fogalmát csak azért vezették be négyzetes mátrixok.

Ha A akkor négyzetmátrix fordított számára a mátrix egy mátrix, amelyet jelölünk A-1és a feltétel kielégítése . (Ezt a meghatározást a számok szorzásával analóg módon vezetjük be)

A $A^(-1)$ mátrixot a $A$ négyzetmátrix inverzének nevezzük, ha $A^(-1)\cdot A=A\cdot A^(-1)=E$, ahol $E $ az azonosságmátrix, melynek sorrendje megegyezik a $A$ mátrix rendjével.

A nem szinguláris mátrix olyan mátrix, amelynek determinánsa nem egyenlő nullával. Ennek megfelelően egy degenerált mátrix az, amelynek determinánsa nulla.

A $A^(-1)$ inverz mátrix akkor és csak akkor létezik, ha a $A$ mátrix nem szinguláris. Ha létezik $A^(-1)$ inverz mátrix, akkor az egyedi.

Számos módszer létezik a mátrix inverzének meghatározására, ezek közül kettőt vizsgálunk meg. Ez az oldal az adjungált mátrix módszert tárgyalja, amely a legtöbb felsőbb matematikai kurzusban standardnak számít. Az inverz mátrix megtalálásának második módját (elemi transzformációk módszere), amely a Gauss-módszer vagy a Gauss-Jordan-módszer használatát foglalja magában, a második részben tárgyaljuk.

Adjungált (uniós) mátrix módszer

Legyen adott a $A_(n\x n)$ mátrix. A $A^(-1)$ inverz mátrix megtalálásához három lépésre van szükség:

Keresse meg a $A$ mátrix determinánsát és győződjön meg arról, hogy $\Delta A\neq 0$, azaz. hogy az A mátrix nem degenerált.
Állítsa össze a $A_(ij)$ algebrai kiegészítéseit a $A$ mátrix minden eleméhez, és írja le a $A_(n\times n)^(*)=\left(A_(ij) \right)$ mátrixot a találtból algebrai komplementerek.
Írjuk fel az inverz mátrixot a $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ képlet figyelembevételével.

A $(A^(*))^T$ mátrixot gyakran az $A$ adjunkt (kölcsönös, szövetséges) mátrixának nevezik.

Ha a döntést manuálisan hozzuk meg, akkor az első módszer csak viszonylag kis sorrendű mátrixokra jó: második (), harmadik (), negyedik (). A magasabb rendű mátrix inverz mátrixának megtalálásához más módszereket használnak. Például a Gauss-módszer, amelyet a második részben tárgyalunk.

1. példa

A mátrix inverzének megkeresése a mátrixhoz $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Mivel a negyedik oszlop minden eleme nulla, akkor $\Delta A=0$ (azaz a $A$ mátrix degenerált). Mivel $\Delta A=0$, nincs mátrix inverze $A$-nak.

Válasz: $A^(-1)$ mátrix nem létezik.

2. példa

Keresse meg a mátrix inverzét: $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Futtasson ellenőrzést.

Az adjungált mátrix módszert használjuk. Először keressük meg az adott $A$ mátrix determinánsát:

$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Mivel $\Delta A \neq 0$, akkor létezik az inverz mátrix, így folytatjuk a megoldást. Algebrai kiegészítések keresése

\begin(igazított) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(igazított)

Állítson össze egy mátrixot algebrai komplementerekből: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transzponálja a kapott mátrixot: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (az eredményül kapott mátrixot gyakran adjungált vagy unió mátrixnak nevezik a $A$ mátrixhoz). A $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ képlet használatával a következőt kapjuk:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

Tehát az inverz mátrix található: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \jobbra) $. Az eredmény igazságosságának ellenőrzéséhez elegendő ellenőrizni az egyik egyenlőség igazságát: $A^(-1)\cdot A=E$ vagy $A\cdot A^(-1)=E$. Ellenőrizzük a $A^(-1)\cdot A=E$ egyenlőséget. Annak érdekében, hogy kevesebbet dolgozzunk a törtekkel, a $A^(-1)$ mátrixot behelyettesítjük, nem a következő formában: $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ de mint $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \ end(tömb )\jobbra)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( tömb)\jobbra)\cdot\left(\begin(tömb) (cc) -5 & 7 \\ 9 & 8 \end(tömb)\jobbra) =-\frac(1)(103)\cdot\left( \begin(tömb) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(tömb )\right) =E $$

Válasz: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

3. példa

Keresse meg a $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$ mátrix inverzét. Futtasson ellenőrzést.

Kezdjük a $A$ mátrix determinánsának kiszámításával. Tehát az $A$ mátrix determinánsa:

$$ \Delta A=\left| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

Mivel $\Delta A\neq 0$, akkor létezik az inverz mátrix, így folytatjuk a megoldást. Megtaláljuk az adott mátrix egyes elemeinek algebrai komplementereit:

Összeállítunk egy mátrixot algebrai összeadásokból, és transzponáljuk:

$$ A^*=\left(\begin(array) (cccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

A $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ képlet használatával kapjuk:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

Tehát $A^(-1)=\left(\begin(array) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. Az eredmény igazságosságának ellenőrzéséhez elegendő ellenőrizni az egyik egyenlőség igazságát: $A^(-1)\cdot A=E$ vagy $A\cdot A^(-1)=E$. Ellenőrizzük a $A\cdot A^(-1)=E$ egyenlőséget. Annak érdekében, hogy kevesebbet dolgozzunk a törtekkel, a $A^(-1)$ mátrixot behelyettesítjük nem a következő formában: $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, de mint $\frac(1)(26)\ cdot \left( \begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(tömb) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(array) \right) =\frac(1)(26)\cdot\left(\begin(array) (cccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (tömb) \jobbra) =\left(\begin(tömb) (cccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

Az ellenőrzés sikeres volt, a $A^(-1)$ inverz mátrix helyesen található.

Válasz: $A^(-1)=\left(\begin(array) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

4. példa

Keresse meg a $A=\left(\begin(tömb) (cccc) mátrix inverzét 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

Negyedrendű mátrix esetén az inverz mátrix megtalálása algebrai összeadásokkal kissé nehézkes. Ilyen példák azonban találhatók az ellenőrző munkákban.

Az inverz mátrix megtalálásához először ki kell számítani a $A$ mátrix determinánsát. Ennek legjobb módja ebben a helyzetben, ha a determinánst sorban (oszlopban) bővítjük. Kijelölünk egy tetszőleges sort vagy oszlopot, és megkeressük a kiválasztott sor vagy oszlop egyes elemeinek algebrai kiegészítését.

Például az első sorhoz a következőket kapjuk:

$$ A_(11)=\left|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\left|\begin(array)(cccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\left|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

Az $A$ mátrix determinánsát a következő képlettel számítjuk ki:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14) )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(igazított) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(igazított) $$

Algebrai komplement mátrix: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(array)\right)$.

Csatolt mátrix: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Inverz mátrix:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Az ellenőrzést, ha szükséges, az előző példákkal megegyező módon lehet elvégezni.

Válasz: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(tömb) \jobbra) $.

A második részben az inverz mátrix megtalálásának egy másik módját vizsgáljuk meg, amely magában foglalja a Gauss-módszer vagy a Gauss-Jordan-módszer transzformációit.

Legyen adott egy négyzetes mátrix. Meg kell találni az inverz mátrixot.

Első út. Az inverz mátrix létezéséről és egyediségéről szóló 4.1. Tétel megjelöli a megtalálásának egyik módját.

1. Számítsa ki az adott mátrix determinánsát! Ha, akkor az inverz mátrix nem létezik (a mátrix degenerált).

2. Készítsen mátrixot a mátrixelemek algebrai komplementereiből!

3. A mátrix transzponálásával kapjuk meg a hozzá tartozó mátrixot .

4. Keresse meg az inverz mátrixot (4.1) úgy, hogy a hozzá tartozó mátrix összes elemét elosztja a determinánssal

A második út. Az inverz mátrix megtalálásához elemi transzformációk használhatók.

1. Készítsen blokkmátrixot az adott mátrix azonossági mátrixhoz való hozzárendelésével azonos sorrendben.

2. A mátrix sorain végrehajtott elemi transzformációk segítségével állítsa a bal oldali blokkját a legegyszerűbb formába. Ebben az esetben a blokkmátrix olyan formára redukálódik, ahol az identitásmátrixból történő transzformációk eredményeként kapott négyzetes mátrix.

3. Ha , akkor blokk egyenlő az inverz mátrixszal, azaz Ha, akkor a mátrixnak nincs inverze.

Valójában egy mátrix sorainak elemi transzformációi segítségével a bal oldali blokkja leegyszerűsített formára redukálható (lásd 1.5. ábra). Ebben az esetben a blokkmátrixot olyan alakra alakítjuk, ahol egy elemi mátrix, amely kielégíti az egyenlőséget. Ha a mátrix nem szinguláris, akkor a 3.3 megjegyzés 2. pontja szerint egyszerűsített formája egybeesik az azonosságmátrixszal. Aztán az egyenlőségből az következik. Ha a mátrix degenerált, akkor az egyszerűsített formája eltér az azonosságmátrixtól, és a mátrixnak nincs inverze.

11. Mátrixegyenletek és megoldásuk. SLAE mátrixjelölése. Mátrix módszer (inverz mátrix módszer) az SLAE megoldására és alkalmazhatóságának feltételei.

A mátrixegyenletek a következő alakú egyenletek: A*X=C; X*A=C; A*X*B=C ahol az A, B, C mátrix ismert, az X mátrix nem ismert, ha az A és B mátrix nem degenerált, akkor az eredeti mátrixok megoldásait a megfelelő formában írjuk fel: X=A-1*C; X=C*A-1; X \u003d A -1 * C * B -1 Lineáris algebrai egyenletek írásrendszerének mátrixformája. Minden SLAE-hez több mátrix társítható; sőt maga az SLAE is felírható mátrixegyenletként. Az SLAE (1) esetében vegye figyelembe a következő mátrixokat:

Az A mátrixot ún rendszermátrix. Ennek a mátrixnak az elemei az adott SLAE együtthatói.

Az A˜ mátrixot nevezzük kiterjesztett mátrix rendszer. Ezt úgy kapjuk meg, hogy a rendszermátrixhoz hozzáadunk egy b1,b2,...,bm szabad tagokat tartalmazó oszlopot. Általában ezt az oszlopot függőleges vonal választja el az áttekinthetőség kedvéért.

A B oszlopmátrixot ún szabad kifejezések mátrixa, és az X oszlopmátrix az ismeretlenek mátrixa.

A fent bemutatott jelöléssel az SLAE (1) felírható mátrixegyenlet formájában: A⋅X=B.

jegyzet

A rendszerhez tartozó mátrixokat többféleképpen is felírhatjuk: minden a vizsgált SLAE változóinak és egyenleteinek sorrendjétől függ. De mindenesetre az ismeretlenek sorrendjének egy adott SLAE minden egyenletében azonosnak kell lennie.

A mátrix módszer olyan SLAE megoldására alkalmas, amelyben az egyenletek száma egybeesik az ismeretlen változók számával, és a rendszer főmátrixának determinánsa nem nulla. Ha a rendszer háromnál több egyenletet tartalmaz, akkor az inverz mátrix megtalálása jelentős számítási ráfordítást igényel, ezért ebben az esetben célszerű a megoldást használni. Gauss módszer.

12. Homogén SLAE-k, nem-nulla megoldásaik létezésének feltételei. Homogén SLAE-k parciális megoldásainak tulajdonságai.

Egy lineáris egyenletet homogénnek nevezünk, ha a szabad tagja nulla, egyébként inhomogénnek. A homogén egyenletekből álló rendszert homogénnek nevezzük, és általános formája:

13 .Egy homogén SLAE parciális megoldásainak lineáris függetlenségének és függésének fogalma. Fundamentális döntési rendszer (FSR) és megállapítása. Egy homogén SLAE általános megoldásának ábrázolása az FSR szempontjából.

Funkciórendszer y 1 (x ), y 2 (x ), …, y n (x ) nak, nek hívják lineárisan függő az intervallumon ( a , b ) ha van olyan állandó együtthatók halmaza, amelyek egyidejűleg nem egyenlőek nullával, úgy, hogy ezeknek a függvényeknek a lineáris kombinációja azonosan egyenlő nullával on ( a , b ): számára. Ha az egyenlőség csak esetén lehetséges, akkor a függvényrendszer y 1 (x ), y 2 (x ), …, y n (x ) nak, nek hívják lineárisan független az intervallumon ( a , b ). Más szóval, a funkciók y 1 (x ), y 2 (x ), …, y n (x ) lineárisan függő az intervallumon ( a , b ) ha létezik nulla a ( a , b ) ezek nem triviális lineáris kombinációja. Funkciók y 1 (x ),y 2 (x ), …, y n (x ) lineárisan független az intervallumon ( a , b ) ha csak triviális lineáris kombinációjuk egyenlő nullával on ( a , b ).

Alapvető döntési rendszer (FSR) egy homogén SLAE az alapja ennek az oszloprendszernek.

Az FSR elemeinek száma egyenlő a rendszerben lévő ismeretlenek számával mínusz a rendszermátrix rangja. Az eredeti rendszer bármely megoldása az FSR megoldásainak lineáris kombinációja.

Tétel

Az inhomogén SLAE általános megoldása egyenlő az inhomogén SLAE konkrét megoldásának és a megfelelő homogén SLAE általános megoldásának összegével.

1 . Ha az oszlopok egy homogén egyenletrendszer megoldásai, akkor ezek bármely lineáris kombinációja egy homogén rendszer megoldása is.

Valójában az egyenlőségekből az következik

azok. megoldások lineáris kombinációja egy homogén rendszer megoldása.

2. Ha egy homogén rendszer mátrixának rangja , akkor a rendszernek lineárisan független megoldásai vannak.

Valójában a homogén rendszer általános megoldásának (5.13) képleteivel konkrét megoldásokat találhatunk, ha a szabad változókhoz a következőket rendeljük alapértelmezett érték beállításai (minden alkalommal feltételezve, hogy a szabad változók egyike egyenlő eggyel, a többi pedig nullával):

amelyek lineárisan függetlenek. Valóban, ha ezekből az oszlopokból mátrixot képezünk, akkor az utolsó sorai alkotják az identitásmátrixot. Ezért az utolsó sorokban található moll nem egyenlő nullával (egyenlő eggyel), azaz. alapvető. Ezért a mátrix rangja egyenlő lesz. Ezért ennek a mátrixnak minden oszlopa lineárisan független (lásd 3.4. Tétel).

Egy homogén rendszer lineárisan független megoldásainak bármely gyűjteményét nevezzük megoldások alaprendszere (halmaza). .

14 th rendű moll, alapmoll, mátrix rang. Mátrix rangszámítás.

Egy A mátrix k-moll rendje a determinánsa néhány k rendű négyzetes részmátrixának.

Egy m x n A mátrixban egy r rendű mollot alapnak nevezünk, ha nem nulla, és minden nagyobb rendű moll, ha létezik, egyenlő nullával.

Az A mátrix azon oszlopait és sorait, amelyek metszéspontjában bázis-moll található, A bázis oszlopainak és sorainak nevezzük.

1. tétel (A mátrix rangjáról). Bármely mátrix esetében a mellékrang egyenlő a sorranggal és az oszlopranggal.

2. tétel (Az alapmollról). A mátrix minden oszlopa az alaposzlopok lineáris kombinációjára bomlik.

A mátrix rangja (vagy minor rangja) az alapmoll sorrendje, vagy más szóval a legnagyobb rend, amelyhez nem nulla mollok léteznek. Egy nulla mátrix rangját értelemszerűen 0-nak tekintjük.

Két nyilvánvaló kisebbségi tulajdonságot figyelünk meg.

1) A mátrix rangja nem változik transzponáláskor, mivel egy mátrix transzponálásakor az összes almátrixa transzponálódik, és a minorok nem változnak.

2) Ha A' az A mátrix egy részmátrixa, akkor az A' rangja nem haladja meg az A rangját, mivel az A'-ben szereplő nem nulla moll is benne van az A-ban.

15. A -dimenziós aritmetikai vektor fogalma. Vektor egyenlőség. Műveletek vektorokon (összeadás, kivonás, szorzás számmal, szorzás mátrixszal). Vektorok lineáris kombinációja.

Rendelt gyűjtemény n valós vagy komplex számokat nevezünk n-dimenziós vektor. A számokat hívják vektor koordináták.

Két (nem nulla) vektor aÉs b egyenlőek, ha egyenlő irányúak és azonos modulusúak. Minden nulla vektort egyenlőnek tekintünk. Minden más esetben a vektorok nem egyenlőek.

Vektorok összeadása. A vektorok hozzáadásának két módja van.1. paralelogramma szabály. Az és vektorok összeadásához mindkettő kezdetét ugyanabba a pontba helyezzük. Befejezzük a paralelogrammát, és ugyanabból a pontból rajzoljuk meg a paralelogramma átlóját. Ez lesz a vektorok összege.

2. A vektorok összeadásának második módja a háromszögszabály. Vegyük ugyanazokat a vektorokat és . A második elejét hozzáadjuk az első vektor végéhez. Most kössük össze az első elejét és a második végét. Ez a vektorok és az összege. Ugyanezen szabály szerint több vektort is hozzáadhat. Egyenként rögzítjük őket, majd összekötjük az első elejét az utolsó végével.

Vektorok kivonása. A vektor a vektorral ellentétes irányban irányul. A vektorok hossza egyenlő. Most már világos, hogy mi a vektorok kivonása. A és a vektorok különbsége a vektor és a vektor összege.

Szorozza meg a vektort egy számmal

Egy vektort k számmal megszorozva olyan vektort kapunk, amelynek hossza k-szor különbözik a hossztól. Egyirányú a vektorral, ha k nagyobb nullánál, és ellentétes irányú, ha k kisebb, mint nulla.

A vektorok skaláris szorzata a vektorok hosszának és a közöttük lévő szög koszinuszának a szorzata. Ha a vektorok merőlegesek, akkor pontszorzatuk nulla. És így fejeződik ki a skaláris szorzat a és a vektorok koordinátáival.

Vektorok lineáris kombinációja

Vektorok lineáris kombinációja hívás vektor

Ahol - lineáris kombinációs együtthatók. Ha egy kombinációt triviálisnak nevezünk, ha nem triviális.

16 .Aritmetikai vektorok skaláris szorzata. A vektor hossza és a vektorok közötti szög. A vektorok ortogonalitásának fogalma.

Az a és b vektor skaláris szorzata a szám

A skaláris szorzat kiszámítására szolgál: 1) a köztük lévő szög meghatározása; 2) a vektorok vetületének meghatározása; 3) a vektor hosszának kiszámítása; 4) a merőleges vektorok feltételei.

Az AB szakasz hossza az A és B pontok közötti távolság. Az A és B vektorok közötti szöget α = (a, c), 0≤ α ≤П szögnek nevezzük. Amivel el kell forgatni 1 vektort úgy, hogy iránya egy másik vektorral essen egybe. Feltéve, ha a kezdetek egybeesnek.

Az orth a egy a vektor, amelynek hossza és iránya egységnyi a.

17. A vektorrendszer és annak lineáris kombinációja. A vektorrendszer lineáris függésének és függetlenségének fogalma. Tétel egy vektorrendszer lineáris függésének szükséges és elégséges feltételeiről.

Az a1,a2,...,an vektorok rendszerét lineárisan függőnek nevezzük, ha vannak olyan λ1,λ2,...,λn számok, amelyek közül legalább az egyik nem nulla, és λ1a1+λ2a2+...+λnan=0 . Egyébként a rendszert lineárisan függetlennek nevezzük.

Két a1 és a2 vektort kollineárisnak nevezünk, ha irányuk azonos vagy ellentétes.

Három a1, a2 és a3 vektort koplanárisnak nevezünk, ha párhuzamosak valamilyen síkkal.

A lineáris függőség geometriai kritériumai:

a) az (a1,a2) rendszer akkor és csak akkor lineárisan függ, ha az a1 és a2 vektorok kollineárisak.

b) az (a1,a2,a3) rendszer akkor és csak akkor lineárisan függ, ha az a1,a2 és a3 vektorok egysíkúak.

tétel. (A lineáris függőség szükséges és elégséges feltétele rendszerek vektorok.)

Vektoros rendszer vektor hely van lineárisan akkor és csak akkor függ, ha a rendszer egyik vektora lineárisan van kifejezve a többivel vektor ezt a rendszert.

Következmény.1. Egy vektortérben lévő vektorrendszer akkor és csak akkor lineárisan független, ha a rendszer egyik vektora sem fejeződik ki lineárisan ennek a rendszernek a többi vektorával.2. Egy nulla vektort vagy két egyenlő vektort tartalmazó vektorrendszer lineárisan függő.