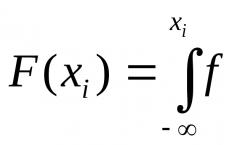ters fonksiyon yöntemi

Sürekli bir rasgele değişken oynamanın gerekli olmasına izin verin X, yani olası değerlerinin sırasını alın X Ben (Ben= 1,2, ...), dağıtım işlevini bilmek F(X).

teorem. Eğer R Ben ,-rastgele sayı, sonra olası değerX Ben sürekli rasgele değişken X, belirli bir dağıtım işleviyle oynanıyorF(X)karşılık gelenR Ben , denklemin köküdür

F(X Ben)= R Ben . (»)

Kanıt. Rastgele bir sayı seçilmesine izin verin R Ben (0≤R Ben <1). Так как в интервале всех возможных зна­чений X dağıtım işlevi F(X) monoton olarak 0'dan 1'e yükselir, o zaman bu aralıkta argümanın böyle bir değeri ve yalnızca bir tane vardır. X Ben , dağıtım fonksiyonunun değeri aldığı yer R Ben. Başka bir deyişle, denklemin (*) tek bir çözümü vardır.

X Ben = F - 1 (R Ben),

Nerede F - 1 - ters fonksiyon y=F(X).

Şimdi kökün olduğunu kanıtlayalım. X Ben denklem (*), böyle sürekli bir rasgele değişkenin olası bir değeridir (geçici olarak şu şekilde göstereceğiz: ξ ve ardından şundan emin olun: ξ=X). Bu amaçla, çarpma olasılığının ξ bir aralığa, örneğin ( İle,D), tüm olası değerlerin aralığına ait X, dağıtım fonksiyonunun artışına eşittir F(X) bu aralıkta:

R(İle< ξ < D)= F(D)- F(İle).

Gerçekten de, beri F(X)- tüm olası değerler aralığında monoton artan fonksiyon X, daha sonra bu aralıkta, argümanın büyük değerleri, fonksiyonun büyük değerlerine karşılık gelir ve bunun tersi de geçerlidir. Bu nedenle, eğer İle <X Ben < D, O F(C)< R Ben < F(D), ve tersi [(*) nedeniyle F(X Ben)=R Ben ].

Bu eşitsizliklerden, rastgele değişkenin ξ aralığın içine alınmış

İle< ξ < D, ξ (**)

sonra rastgele değişken R aralığın içine alınmış

F(İle)< R< F(D), (***)

ve geri Bu nedenle, (**) ve (***) eşitsizlikleri eşdeğerdir ve bu nedenle eşit derecede olasıdır:

R(İle< ξ< D)=P[F(İle)< R< F(D)]. (****)

değerden beri R(0,1) aralığında düzgün dağılmış, ardından isabet olasılığı R(0,1) aralığına ait bir aralığın uzunluğuna eşittir (bkz. Bölüm XI, § 6, açıklama). Özellikle,

R[F(İle)< R< F(D) ] = F(D) - F(İle).

Bu nedenle bağıntı (****) şu şekilde yazılabilir:

R(İle< ξ< D)= F(D) - F(İle).

Yani çarpma olasılığı ξ aralığa ( İle,D) dağıtım fonksiyonunun artışına eşittir F(X) bu aralıkta, yani ξ=X. Başka bir deyişle, sayılar X Ben, formül (*) ile tanımlanan, miktarın olası değerleri vardır X ler verilen dağılım fonksiyonu F(X), Q.E.D.

Kural 1X Ben , sürekli rastgele değişken X, dağıtım işlevini bilmek F(X), rastgele bir sayı seçmelisin R Ben dağılım fonksiyonlarını eşitleyin ve için çözün X Ben , sonuç denklemi

F(X Ben)= R Ben .

Açıklama 1. Bu denklem açık bir şekilde çözülemezse, grafiksel veya sayısal yöntemlere başvurulur.

Örnek 1 Sürekli bir rasgele değişkenin 3 olası değerini oyna X,(2, 10) aralığında düzgün dağılmıştır.

Çözüm. Miktarın dağılım fonksiyonunu yazalım. X, aralığında düzgün dağılmış ( A,B) (bkz. Bölüm XI, § 3, örnek):

F(X)= (Ha)/ (B-A).

Koşula göre, bir = 2, B=10, bu nedenle,

F(X)= (X- 2)/ 8.

Bu bölümün kuralını kullanarak olası değerleri bulmak için bir denklem yazıyoruz. X Ben , bunun için dağıtım fonksiyonunu rastgele bir sayıya eşitliyoruz:

(X Ben -2 )/8= R Ben .

Buradan X Ben =8 R Ben + 2.

Örneğin 3 rastgele sayı seçelim, R Ben =0,11, R Ben =0,17, R Ben= 0.66. Bu sayıları, şuna göre çözülmüş denklemde değiştirin: X Ben , sonuç olarak, karşılık gelen olası değerleri elde ederiz X: X 1 \u003d 8 0,11 + 2 \u003d\u003d 2,88; X 2 =1.36; X 3 = 7,28.

Örnek 2 Sürekli rastgele değişken X dağılım fonksiyonu tarafından verilen üstel yasaya göre dağıtılır (λ > 0 parametresi bilinir)

F(X)= 1 - e - λ X (x>0).

Olası değerleri oynatmak için açık bir formül bulmak gerekir. X.

Çözüm. Bu paragrafın kuralını kullanarak denklemi yazıyoruz

1 - e - λ X Ben

için bu denklemi çözelim X Ben :

e - λ X Ben = 1 - R Ben, veya - λ X Ben = ln(1 - R Ben).

X Ben =1p(1– R Ben)/λ .

Rastgele sayı R Ben(0,1) aralığı içine alınır; dolayısıyla 1 sayısı - R Ben, ayrıca rastgele ve (0,1) aralığına aittir. Başka bir deyişle, miktarlar R ve 1- R eşit olarak dağıtılır. Bu nedenle, bulmak için X Ben Daha basit bir formül kullanabilirsiniz:

X Ben =- ln R Ben /λ.

Açıklama 2. Bilindiği gibi (bkz. Bölüm XI, §3)

Özellikle,

Olasılık yoğunluğu biliniyorsa, F(X), sonra oynamak için X denklemler yerine F(X Ben)=R Ben karar verilen X Ben denklem

Kural 2 Olası bir değeri bulmak için X Ben (sürekli rastgele değişken X, olasılık yoğunluğunu bilmek F(X) rastgele bir sayı seçin R Ben ve karar ver X Ben , denklem

veya denklem

Nerede A- mümkün olan en küçük son değer X.

Örnek 3 Sürekli bir rasgele değişkenin olasılık yoğunluğu göz önüne alındığında XF(X)=λ (1-λx/2) (0; 2/λ) aralığında; bu aralığın dışında F(X)= 0. Olası değerleri oynatmak için açık bir formül bulmak gerekir. X.

Çözüm. Kural 2'ye göre denklemi yazıyoruz

Ortaya çıkan ikinci dereceden denklemi entegre edip çözdükten sonra X Ben, sonunda aldık

LABORATUVAR ÇALIŞMASI MM-03

AYRIK VE SÜREKLİ ROV'LARDA OYNAMA

Çalışmanın amacı: ayrık ve sürekli RV'leri oynatmak için yöntemlerin incelenmesi ve yazılım uygulaması

DERS ÖZETİNDEN ÇALIŞACAK SORULAR:

1. Ayrık rastgele değişkenler ve özellikleri.

2. Rastgele olaylardan oluşan eksiksiz bir grup oynamak.

3. Ters fonksiyon yöntemiyle sürekli bir rasgele değişkeni oynatmak.

4. Uzayda rastgele bir yön seçimi.

5. Standart normal dağılım ve verilen parametreler için yeniden hesaplanması.

6. Normal dağılımı göstermek için kutupsal koordinat yöntemi.

GÖREV 1. Dağıtım yasası bir tablo şeklinde verilen ayrı bir RV'nin değerlerini oynatmak için bir kural (yazılı olarak) formüle edin. RNG alt programından alınan BSV'yi kullanarak CV değerlerini oynatmak için bir alt program işlevi oluşturun. 50 CB değerini oynatın ve ekranda görüntüleyin.

Burada N varyant numarasıdır.

GÖREV 2. Sürekli bir rasgele değişken X'in dağılım yoğunluk fonksiyonu f(x) verilmiştir.

Raporda, formülleri ve aşağıdaki değerlerin hesaplanmasını yazın:

A) normalleştirme sabiti;

B) dağılım fonksiyonu F(x);

C) matematiksel beklenti M(X);

D) dağılım D(X);

E) ters fonksiyon yöntemini kullanarak CB'nin değerlerini oynamak için bir formül.

Verilen CV'yi oynatmak ve bu CV'nin 1000 değerini almak için bir fonksiyon alt programı oluşturun.

Elde edilen sayıların 20 segment üzerinden dağılımının bir histogramını oluşturun.

GÖREV 3. Uzayda rastgele bir yönün parametrelerini oynatmanıza izin veren bir prosedür yazın. Uzayda 100 rastgele yön oynayın.

Yerleşik sözde rasgele sayı üretecini kullanın.

Laboratuvar çalışmasına ilişkin yazılı rapor şunları içermelidir:

1) Çalışmanın adı ve amacı, öğrencinin grubu, soyadı ve numarası seçeneği;

2) Her görev için: -koşul, -gerekli formüller ve matematiksel dönüşümler, -kullanılan algoritmayı uygulayan program dosyasının adı, -hesaplama sonuçları.

Hata ayıklanan program dosyaları yazılı raporla birlikte teslim edilir.

BAŞVURU

Sürekli SW'nin dağıtım yoğunluğunun varyantları

Var-t	SW dağıtım yoğunluğu	Var-t	SW dağıtım yoğunluğu

Monte Carlo yönteminin özü şudur: değeri bulmanız gerekir A incelenmekte olan bazı değerler. Bu amaçla, matematiksel beklentisi a'ya eşit olan böyle bir rastgele değişken X seçilir: M(X)=a.

Pratikte bunu yaparlar: hesaplarlar (oynatırlar) N rastgele bir X değişkeninin olası değerleri x i, aritmetik ortalamalarını bulun

Ve bir tahmin (yaklaşık değer) olarak istenen a sayısının bir * değerini alırlar. Bu nedenle Monte Carlo yöntemini uygulamak için rastgele bir değişkeni oynayabilmek gerekir.

Ayrık bir rasgele değişken X'i oynatmak istensin, yani. X dağılım yasasını bilerek x i (i=1,2, …) olası değerlerinin sırasını hesaplayın. Gösterimi tanıtalım: R, (0,1) aralığında tek tip olarak dağıtılan sürekli bir rasgele değişkendir; r ben (j=1,2,…) – rastgele sayılar (R'nin olası değerleri).

Kural: Dağılım yasası tarafından verilen ayrık bir X rasgele değişkenini oynatmak için

x x 1 x 2 ... x n

P p 1 p 2 … p n

1. veya ekseninin aralığını (0,1) n kısmi aralığa bölün:

Δ 1 = (0; p 1), Δ 2 = (p 1; p 1+ p 2), ..., Δ n = (p 1 + p 2 + ... + p n -1; 1).

2. Rastgele bir sayı seçin rj . Eğer rj kısmi Δi aralığına düşerse, oynatılan değer olası xi değerini alır. .

Tam bir etkinlik grubunu oynatma

Her birinde tam grubun olaylarından birinin meydana geldiği, olasılıkları bilinen testler oynamak gerekir. Tam bir olay grubunu oynatmak, ayrık bir rasgele değişkeni oynatmaya indirgenir.

Kural: Tüm grubun A 1, A 2, ..., An olaylarından birinin meydana geldiği, p 1, p 2, ..., p n olasılıklarının bilindiği testlerin oynanabilmesi için, aşağıdaki dağılım yasası ile ayrık bir X değerinin oynanması yeterlidir:

P p 1 p 2 … p n

Testte X değeri olası x i = i değerini aldıysa, o zaman A i olayı meydana geldi.

Sürekli Rastgele Değişken Oynatma

Sürekli bir rasgele değişken X'in dağılım fonksiyonu F biliniyor, X'i oynamak gerekiyor, yani. x i (i=1,2, …) olası değerlerin sırasını hesaplayın.

A. Ters fonksiyonlar yöntemi. Kural 1 sürekli bir rasgele değişken X'in x i, dağılım fonksiyonunu F bilerek, bir rasgele sayı r i seçmeniz, dağılım fonksiyonunu eşitlemeniz ve x i için elde edilen F(х i) = r ben denklemini çözmeniz gerekir.

Olasılık yoğunluğu f(x) biliniyorsa, kural 2 kullanılır.

Kural 2 Olası anlamı oynamak için x i sürekli bir rasgele değişken X, onun olasılık yoğunluğunu f bilerek, bir rasgele sayı r i seçmeniz ve x i için denklemi çözmeniz gerekir

veya denklem

burada a, X'in mümkün olan en küçük sonlu değeridir.

B. Süperpozisyon yöntemi. Kural 3 Dağılım fonksiyonu olan X rasgele değişkeninin olası değerini oynamak için

F(x) = C 1 F 1 (x)+C 2 F 2 (x)+…+C n F n (x),

burada F k (x) – dağılım fonksiyonları (k=1, 2, …, n), С k >0, С i +С 2 +…+С n =1, iki bağımsız rasgele sayı r 1 ve r 2 seçmek ve yardımcı ayrık rasgele değişken Z'nin olası değerini oynamak için r 1 rasgele sayısını kullanmak gerekir (kural 1'e göre):

p C 1 C 2 … C n

Z=k olduğu ortaya çıkarsa, x için F k (x) = r 2 denklemi çözülür.

Açıklama 1. Sürekli bir rasgele değişken X'in olasılık yoğunluğu şu şekilde verilirse

f(x)=C 1 f 1 (x)+C 2 f 2 (x)+…+C n f n (x),

burada f k olasılık yoğunluklarıdır, C k katsayıları pozitiftir, toplamları bire eşittir ve Z=k olduğu ortaya çıkarsa, o zaman (kural 2'ye göre) x'e göre çözerler ben veya denkleme göre

Normal bir rasgele değişkenin yaklaşık olarak oynatılması

Kural. Olası değere yaklaşmak için a=0 ve σ=1 parametrelerine sahip normal bir rasgele değişken X'in x i'si, 12 bağımsız rasgele sayı ekleyin ve elde edilen toplamdan 6 çıkarın:

Yorum. Matematiksel beklenti ile normal bir rasgele değişken Z'yi yaklaşık olarak oynamak istiyorsanız A ve standart sapma σ, daha sonra, yukarıdaki kurala göre x i'nin olası değerini oynadıktan sonra, aşağıdaki formüle göre istenen olası değeri bulurlar: z i = σx i +a.

Tanım 24.1.rastgele numaralar olası değerleri adlandırın R sürekli rastgele değişken R, (0; 1) aralığında düzgün bir şekilde dağılmıştır.

1. Ayrı bir rasgele değişkenin oynatılması.

Ayrık bir rasgele değişkeni oynatmak istensin X, yani dağıtım yasasını bilerek olası değerlerinin bir dizisini elde etmek X:

x x 1 X 2 … x n

pp 1 R 2 … rp .

(0, 1)'de düzgün dağılmış rastgele bir değişken düşünün R ve aralığı (0, 1) koordinatlı noktalara bölün R 1, R 1 + R 2 , …, R 1 + R 2 +… +rp-1 açık P uzunlukları aynı indekslere sahip olasılıklara eşit olan kısmi aralıklar.

Teorem 24.1. Aralığa düşen her rasgele sayıya olası bir değer atanırsa, çalınan değerin belirli bir dağıtım yasası olacaktır:

x x 1 X 2 … x n

pp 1 R 2 … rp .

Kanıt.

Elde edilen rasgele değişkenin olası değerleri küme ile çakışmaktadır. X 1 , X 2 ,… x n, çünkü aralık sayısı P ve vurulduğunda rj aralığında, rastgele bir değişken değerlerden yalnızca birini alabilir X 1 , X 2 ,… x n.

Çünkü R düzgün dağılmışsa, o zaman her aralığa düşme olasılığı uzunluğuna eşittir, bu da her değerin olasılığa karşılık geldiği anlamına gelir. pi. Böylece, oynanan rasgele değişkenin belirli bir dağıtım yasası vardır.

Örnek. Ayrı bir rasgele değişkenin 10 değerini oyna X, dağıtım yasası şu şekildedir: X 2 3 6 8

R 0,1 0,3 0,5 0,1

Çözüm. (0, 1) aralığını kısmi aralıklara ayıralım: D 1 - (0; 0.1), D 2 - (0.1; 0.4), D 3 - (0.4; 0.9), D 4 - (0.9; 1). Rastgele sayılar tablosundan 10 sayı yazalım: 0.09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0.34. Birinci ve yedinci sayılar D1 aralığında yer alır, bu nedenle bu durumlarda oynanan rasgele değişken şu değeri almıştır: X 1 = 2; üçüncü, dördüncü, sekizinci ve onuncu sayılar, şuna karşılık gelen D2 aralığına düştü X 2 = 3; ikinci, beşinci, altıncı ve dokuzuncu sayılar D3 aralığındaydı - iken x = x 3 = 6; son aralığa tek bir sayı düşmedi. Yani, oynanmış olası değerler X 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. Zıt olayları oynamak.

Her birinde olayın olduğu denemeleri oynamak istensin A bilinen bir olasılıkla ortaya çıkıyor R. Ayrı bir rasgele değişken düşünün X 1 değerlerini alan (eğer olay A oldu) bir olasılıkla R ve 0 (eğer A olmadı) bir olasılıkla Q = 1 – P. Ardından, önceki paragrafta önerildiği gibi bu rastgele değişkeni oynarız.

Örnek. Her biri bir etkinlik içeren 10 meydan okuma oynayın A 0.3 olasılıkla görünür.

Çözüm. Rastgele bir değişken için X dağıtım kanunu ile X 1 0

R 0,3 0,7

D 1 - (0; 0.3) ve D 2 - (0.3; 1) aralıklarını alıyoruz. Önceki örnekte olduğu gibi aynı rasgele sayı örneğini kullanıyoruz, bunun için №№1,3 ve 7 sayıları D 1 aralığına ve geri kalanı - D 2 aralığına düşüyor. Bu nedenle, olayın olduğunu varsayabiliriz. A birinci, üçüncü ve yedinci denemelerde oldu, ancak diğerlerinde olmadı.

3. Eksiksiz bir etkinlik grubunu oynatmak.

eğer olaylar A 1 , A 2 , …, bir p olasılıkları eşit olan R 1 , R 2 ,… rp, tam bir grup oluşturun, ardından oynamak için (yani, bir dizi testte görünüşlerinin sırasını modellemek), ayrı bir rasgele değişkeni oynatabilirsiniz. X dağıtım kanunu ile X 1 2 … P, bunu 1. paragraftaki gibi yapıyoruz. Aynı zamanda şunu varsayıyoruz:

pp 1 R 2 … rp

Eğer X değer alır x ben = ben, sonra bu denemede bir olay meydana geldi bir ben.

4. Sürekli bir rasgele değişken oynamak.

a) Ters fonksiyonlar yöntemi.

Sürekli bir rasgele değişken oynamanın gerekli olmasına izin verin X, yani olası değerlerinin sırasını alın x ben (Ben = 1, 2, …, N), dağıtım işlevini bilmek F(X).

Teorem 24.2. Eğer ri rastgele bir sayıdır, o zaman olası değer x ben sürekli rasgele değişken oynadı X belirli bir dağıtım fonksiyonu ile F(X), karşılık gelen ri, denklemin köküdür

F(x ben) = ri. (24.1)

Kanıt.

Çünkü F(X) 0 ile 1 aralığında monoton olarak artarsa, bağımsız değişkenin (ve benzersiz) bir değeri vardır x ben, dağıtım işlevinin değeri aldığı yer ri. Dolayısıyla, denklem (24.1) benzersiz bir çözüme sahiptir: x ben= F -1 (ri), Nerede F-1 - işlevin tersi F. Denklem kökünün (24.1) dikkate alınan rasgele değişkenin olası bir değeri olduğunu kanıtlayalım. X.İlk önce varsayalım x ben bazı rasgele değişken x'in olası bir değeridir ve x'in aralığa düşme olasılığının ( c, d) eşittir F(D) – F(C). Aslında monotonluktan dolayı F(X) ve şu F(x ben) = ri. Daha sonra

Bu nedenle, Dolayısıyla, x'in () aralığına düşme olasılığı c, d) dağıtım fonksiyonunun artışına eşittir F(X) bu aralıkta, dolayısıyla x = X.

Sürekli bir rasgele değişkenin 3 olası değerini oyna X, (5; 8) aralığında düzgün bir şekilde dağılmıştır.

F(X) = , yani denklemi çözmek gerekiyor Rastgele 3 sayı seçelim: 0.23; 0.09 ve 0.56 ve onları bu denklemde yerine koy. Karşılık gelen olası değerleri alın X:

b) Süperpozisyon yöntemi.

Oynatılan rasgele değişkenin dağıtım işlevi, iki dağıtım işlevinin doğrusal bir kombinasyonu olarak gösterilebilirse:

o zaman, çünkü X®¥ F(X) ® 1.

Yardımcı bir ayrık rasgele değişken tanıtıyoruz Z dağıtım kanunu ile

Z 12. 2 bağımsız rastgele sayı seçelim R 1 ve R 2 ve olası olanı oynayın

bilgisayar 1 C 2

Anlam Z numaraya göre R 1 (bkz. paragraf 1). Eğer Z= 1, o zaman istenen olası değeri arıyoruz X denklemden ve eğer Z= 2, sonra denklemi çözeriz.

Bu durumda, oynanan rasgele değişkenin dağılım fonksiyonunun, verilen dağılım fonksiyonuna eşit olduğu kanıtlanabilir.

c) Normal bir rasgele değişkenin yaklaşık simülasyonu.

Den beri-dir R, (0, 1) içinde düzgün dağılmış, sonra toplam için P bağımsız, düzgün dağılımlı (0,1) aralığında rasgele değişkenler. Daha sonra, merkezi limit teoremi sayesinde, normalize edilmiş rasgele değişken P® ¥ parametreleri ile normale yakın bir dağılıma sahip olacaktır. A= 0 ve s =1. Özellikle, için oldukça iyi bir yaklaşım elde edilir. P = 12:

Bu nedenle, normalleştirilmiş normal rasgele değişkenin olası değerini oynamak için X, 12 bağımsız rasgele sayı eklemeniz ve toplamdan 6 çıkarmanız gerekir.

İyi çalışmalarınızı bilgi bankasına göndermek basittir. Aşağıdaki formu kullanın

Bilgi tabanını çalışmalarında ve işlerinde kullanan öğrenciler, lisansüstü öğrenciler, genç bilim adamları size çok minnettar olacaklar.

http://www.allbest.ru/ adresinde barındırılmaktadır

1. AKTİVİTE

Belirli bir dağıtım yasasıyla rastgele olayların simülasyonu

Ayrık Rastgele Değişken Oynatma

Ayrı bir rasgele değişkeni oynatmak istensin, örn. dağılım yasasını bilerek x i (i = 1,2,3,...n) olası değerlerinin sırasını elde edin:

Sürekli bir rasgele değişkeni R ile gösterin. R'nin değeri (0,1) aralığında düzgün bir şekilde dağılmıştır. Rastgele değişken R'nin olası değerlerini r j (j = 1,2,...) ile belirtin. 0 aralığını bölelim< R < 1 на оси 0r точками с координатами на n частичных интервалов.

Sonra şunu elde ederiz:

Görüldüğü gibi i indeksli kısmi aralığın uzunluğu, aynı indeksli Р olasılığına eşittir. Uzunluk

Böylece, bir r i rasgele sayısı aralığa düştüğünde, rasgele değişken X, P i olasılığıyla x i değerini alır.

Aşağıdaki teorem vardır:

Aralığa düşen her rasgele sayıya olası bir x i değeri atanırsa, o zaman oynanan değerin belirli bir dağıtım yasası olacaktır.

Dağılım yasası tarafından verilen ayrı bir rasgele değişkeni oynatmak için algoritma

1. 0r ekseninin (0,1) aralığını n kısmi aralığa bölmek gerekir:

2. Rastgele bir sayı seçin (örneğin, bir rasgele sayılar tablosundan veya bir bilgisayarda) rj .

Eğer r j aralığa düşerse, o zaman çalınmakta olan ayrık rasgele değişken x i olası değerini alıyordu.

Sürekli Rastgele Değişken Oynatma

Sürekli bir rasgele değişken X oynaması istensin, yani olası değerlerinin sırasını alın x ben (i = 1,2,...). Bu durumda, dağılım fonksiyonu F(X) bilinmektedir.

var Sonraki teorem.

Eğer r i rasgele bir sayıysa, o zaman bilinen bir dağılım fonksiyonu olan F(X) ile oynanan sürekli rasgele değişken X'in olası değeri x i, r i'ye karşılık gelir denklemin köküdür

Sürekli bir rasgele değişkeni oynatmak için algoritma:

1. Rastgele bir sayı seçmek gereklidir r i .

2. Bilinen dağılım fonksiyonu F(X)'in seçilen rasgele sayısını eşitleyin ve denklemi elde edin.

3. x i için bu denklemi çözün. Ortaya çıkan x i değeri aynı anda rastgele bir sayı r i'ye karşılık gelecektir. ve verilen dağıtım yasası F(X).

Örnek. (2; 10) aralığında düzgün bir şekilde dağıtılan X sürekli rasgele değişkeninin 3 olası değerini oynayın.

X'in dağılım işlevi aşağıdaki forma sahiptir:

Koşula göre, a = 2, b = 10, bu nedenle,

Sürekli bir rasgele değişkeni oynatma algoritmasına uygun olarak, F(X)'i seçilen r i rasgele sayısına eşitleriz. Bundan şunu elde ederiz:

Bu sayıları denklemde değiştirin (5.3).Karşılık gelen olası x değerlerini elde ederiz:

Belirli bir dağılım yasasıyla rastgele olayları modellemeye yönelik problemler

1. Ayrık bir rasgele değişkenin 10 değerini oynatmak gerekir, yani. dağıtım yasasını bilerek x i (i=1,2,3,…n) olası değerlerinin bir dizisini elde edin Х

Rastgele sayılar tablosundan bir rastgele sayı seçelim r j: 0.10; 0,12; 0,37; 0,09; 0,65; 0,66; 0,99; 0,19; 0,88; 0,59; 0,78

2. Hizmet başvurularının alınma sıklığı üstel dağılım yasasına tabidir () , x, l parametresi bilinmektedir (bundan sonra l = 1/t - başvuruların alınma yoğunluğu)

l=0,5 istek/saat. Başvuruların alınması arasındaki aralıkların süresi boyunca değer sırasını belirleyin. Gerçekleşme sayısı 5'e eşittir. Sayı r j: 0.10; 0,12; 0,37; 0,09; 0,65; 0,99;

ETKİNLİK 2

Kuyruk sistemi

Bir yandan her türlü hizmetin yerine getirilmesi için toplu isteklerin olduğu, diğer yandan bu isteklerin karşılandığı sistemlere kuyruk sistemleri denir. Herhangi bir QS, talep akışını yerine getirmeye hizmet eder.

QS şunları içerir: bir gereksinim kaynağı, bir gelen akış, bir kuyruk, bir hizmet cihazı, giden bir istek akışı.

SMO'lar ayrılır:

Kayıplı QS (başarısızlıklar)

Bekleyen CMO (sınırsız kuyruk uzunluğu)

Sınırlı kuyruk uzunluğuna sahip QS

Sınırlı bekleme süresi olan CMO.

Kanal veya servis cihazı sayısına göre, QS tek kanallı ve çok kanallıdır.

Gereksinim kaynağının konumuna göre: açık ve kapalı.

Gereksinim başına servis elemanı sayısına göre: tek fazlı ve çok fazlı.

Sınıflandırma biçimlerinden biri de D. Kendall - A / B / X / Y / Z sınıflandırmasıdır.

A - varışlar arasındaki zamanın dağılımını belirler;

B - hizmet süresinin dağılımını belirler;

X - hizmet kanallarının sayısını belirler;

Y - sistem verimini belirler (kuyruk uzunluğu);

Z - servis sırasını belirler.

Sistem kapasitesi sonsuz olduğunda ve servis siparişi ilk gelen alırsa, Y/Z parçaları atlanır. İlk rakam (A) aşağıdaki karakterleri kullanır:

M dağılımının üstel bir yasası vardır,

G - hizmet süreci hakkında herhangi bir varsayımın olmaması veya tekrarlayan bir hizmet süreci anlamına gelen GI sembolü ile tanımlanır,

D- deterministik (hizmet süresi sabittir),

Е n - n'inci mertebeden Erlangian,

NM n - n'inci mertebeden hiper-Erlangian.

İkinci rakam (B) aynı karakterleri kullanır.

Dördüncü basamak (Y) tamponun kapasitesini gösterir, yani. sıradaki maksimum koltuk sayısı.

Beşinci hane (Z), bekleyen bir sistemde sıradan seçme yöntemini gösterir: SP-eşleştirilebilir, FF-ilk giren-ilk çıkar, LF-son giren-ilk çıkar, PR-önceliği.

görevler için:

l - birim zamanda gelen ortalama başvuru sayısı

µ, birim zaman başına sunulan ortalama istek sayısıdır

Kanal 1 yük faktörü veya bir kanalın meşgul olduğu sürenin yüzdesi.

Temel özellikleri:

1) P ref - arıza olasılığı - sistemin hizmeti reddetme ve gereksinimin kaybolma olasılığı. Bu, kanal veya tüm kanallar meşgul olduğunda (PSTN) gerçekleşir.

Çok kanallı bir QS için R otk = Rn, burada n, hizmet kanallarının sayısıdır.

Sınırlı kuyruk uzunluğu Р otk =Р n + l olan bir QS için, burada l izin verilen kuyruk uzunluğudur.

2) Bağıl q ve sistemin mutlak A verimi

q \u003d 1-P otk A \u003d ql

3) Sistemdeki toplam gereksinim sayısı

L sys = n - QS için başarısızlıklarla, n, hizmet tarafından kullanılan kanal sayısıdır.

Bekleyen ve sınırlı kuyruk uzunluğuna sahip QS için

L sys \u003d n + L harika

burada L exp, hizmetin başlamasını bekleyen ortalama istek sayısıdır, vb.

Kalan özellikler problem çözme sürecinde dikkate alınacaktır.

Tek kanallı ve çok kanallı kuyruk sistemleri. Arıza sistemleri.

Olasılığa dayalı bir girdi akışına ve bir hizmet prosedürüne sahip en basit tek kanallı model, hem hasarların gelişleri arasındaki aralık sürelerinin hem de hizmet sürelerinin üstel dağılımı ile karakterize edilen bir modeldir. Bu durumda, istemlerin gelişleri arasındaki aralıkların sürelerinin dağılım yoğunluğu şu şekildedir:

Hizmet süresi dağıtım yoğunluğu:

İstek ve hizmet akışları en basit olanıdır. Sistemin arızalarla çalışmasına izin verin. Bu tür QS, yerel ağlardaki iletim kanallarının modellenmesinde kullanılabilir. Sistemin mutlak ve bağıl verimini belirlemek gereklidir. Bu kuyruk sistemini iki durumu olan bir grafik (Şekil 2) olarak gösterelim:

S 0 - kanal boş (bekliyor);

S 1 - kanal meşgul (isteğe hizmet veriliyor).

Şekil 2. Arızalı tek kanallı QS durumlarının grafiği

Durumların olasılıklarını belirleyelim: P 0 (t) - "kanal boş" durumunun olasılığı; P 1 (t) - "kanal meşgul" durumunun olasılığı. Etiketli durum grafiğine dayanarak, durum olasılıkları için bir Kolmogorov diferansiyel denklem sistemi oluşturuyoruz:

Doğrusal diferansiyel denklemler sisteminin, P 0 (t) + P 1 (t) = 1 normalleştirme koşuluna tabi bir çözümü vardır. Bu sistemin çözümü durağan değildir, çünkü doğrudan t'ye bağlıdır ve şöyle görünür:

P 1 (t) = 1 - P 0 (t) (3.4.3)

Arızalı tek kanallı bir QS için P 0 (t) olasılığının sistemin q göreli kapasitesinden başka bir şey olmadığını görmek kolaydır. Aslında, P 0, t zamanında kanalın boş olması ve t zamanında gelen iddiaya hizmet verilmesi olasılığıdır ve bu nedenle, belirli bir t süresi için, hizmet verilen hasar sayısının gelen talep sayısına ortalama oranı da P 0 (t), yani q = P 0 (t)'ye eşittir.

Uzun bir zaman aralığından (at) sonra, durağan (sabit durum) moda ulaşılır:

Göreceli verimi bilmek, mutlak olanı bulmak kolaydır. Mutlak verim (A) - kuyruk sisteminin birim zamanda hizmet verebileceği ortalama uygulama sayısı:

İsteğe hizmet vermeyi reddetme olasılığı, "kanal meşgul" durumunun olasılığına eşit olacaktır:

Bu P otk değeri, gönderilenler arasında karşılanmayan isteklerin ortalama payı olarak yorumlanabilir.

Vakaların ezici çoğunluğunda, pratikte, kuyruk sistemleri çok kanallıdır ve bu nedenle, n hizmet veren kanallı modeller (n>1 olduğunda) şüphesiz ilgi çekicidir. Bu model tarafından açıklanan kuyruklama süreci, giriş akışının yoğunluğu ile karakterize edilirken, n'den fazla müşteriye (istek) paralel olarak hizmet verilemez. Bir istek için ortalama hizmet süresi 1/dk'dır. Giriş ve çıkış akışları Poisson'dur. Bir veya başka bir hizmet kanalının çalışma modu, sistemin diğer hizmet kanallarının çalışma modunu etkilemez ve kanalların her biri için hizmet prosedürünün süresi, üstel dağıtım yasasına tabi rastgele bir değişkendir. Paralel bağlı n hizmet kanalını kullanmanın nihai amacı, (tek kanallı bir sisteme kıyasla) n istemciye aynı anda hizmet vererek isteklere hizmet verme hızını artırmaktır. Arızalı çok kanallı bir kuyruk sisteminin durum grafiği Şekil 4'te gösterilen forma sahiptir.

Şekil 4. Çok kanallı bir QS'nin arızalı durumlarının grafiği

S 0 - tüm kanallar ücretsizdir;

S 1 - bir kanal meşgul, geri kalanı boş;

S k - tam olarak k kanal dolu, gerisi boş;

S n - tüm n kanallar dolu, geri kalanlar boş.

P 0 , ... ,P k , ... P n durumlarının sistem olasılıkları için Kolmogorov denklemleri aşağıdaki forma sahip olacaktır:

Sistemi çözmek için başlangıç ​​koşulları aşağıdaki gibidir:

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0 .

Sistemin durağan çözümü şu şekildedir:

P k (3.5.1) olasılıklarını hesaplama formüllerine Erlang formülleri denir.

Durağan bir modda arızalı çok kanallı bir QS'nin işleyişinin olasılıksal özelliklerini belirleyelim:

1) başarısızlık olasılığı:

n kanalın tamamı meşgulken istek gelirse reddedilir. P otk değeri, gelen akışın hizmetinin eksiksizliğini karakterize eder;

2) başvurunun hizmet için kabul edilme olasılığı (aynı zamanda sistemin q göreli verimidir) P otk'u bire tamamlar:

3) mutlak bant genişliği

4) hizmet tarafından işgal edilen ortalama kanal sayısı () aşağıdaki gibidir:

Değer, QS'nin yüklenme derecesini karakterize eder.

Görevler2. derse

1. Bir kanalı olan iletişim kolu, saniyede n = 0,08 mesaj yoğunluğuyla en basit mesaj akışını alır. İletim süresi, exp yasasına göre dağıtılır. Bir mesajın servisi, µ=0.1 yoğunluğu ile gerçekleşir. Hizmet veren kanalın daha önce alınan bir mesajı iletmekle meşgul olduğu zamanlarda gelen mesajlar, bir iletim hatası alır.

katsayı. Bağıl kanal yükü (kanalın meşgul olma olasılığı)

P

Q, düğümler arası dalın göreli kapasitesidir

Ve iletişim kolunun mutlak bant genişliği.

2. İletişim şubesinin bir kanalı vardır ve her 10 saniyede bir mesaj alır. Bir mesajın servis süresi 5 saniyedir. Mesaj iletim süresi üstel olarak dağıtılır. Kanalın meşgul olduğu saatlerde gelen mesajların servisi reddedilir.

Tanımlamak

Р zan - iletişim kanalının doluluk olasılığı (bağıl yük faktörü)

Q- göreli bant genişliği

A, iletişim dalının mutlak bant genişliğidir

4. İkincil iletişim ağının düğümler arası şubesi n = 4 kanala sahiptir. İletişim kolunun kanalları üzerinden iletilmek üzere gelen mesajların akışının hızı = saniyede 8 mesajdır. Bir mesajın ortalama iletim süresi t = 0,1 saniyedir.N kanalın tamamı meşgul olduğu anda gelen bir mesaj, iletişim kolu boyunca bir iletim hatası alır. CMO özelliklerini bulun:

ETKİNLİK 3

Beklemeli tek kanallı sistem

Şimdi beklenti ile tek kanallı bir QS düşünün. Kuyruk sistemi tek kanallıdır. Gelen hizmet istekleri akışı, yoğunluğa sahip en basit akıştır. Hizmet akışının yoğunluğu eşittir (yani, ortalama olarak, sürekli meşgul bir kanal, hizmet verilen istekler gönderir). Hizmet süresi, üstel dağılım yasasına tabi rastgele bir değişkendir. Hizmet akışı, olayların en basit Poisson akışıdır. Kanalın meşgul olduğu bir zamanda gelen istek kuyruğa alınır ve hizmet bekler. Bu QS, modellemede en yaygın olanıdır. Bir veya daha fazla yaklaşımla, bir yerel alan ağının (LAN) hemen hemen her düğümünü simüle etmek için kullanılabilir.

Varsayalım ki hizmet veren sistemin girdisine kaç istek girerse girsin, bu sistem (kuyruk + hizmet verilen istemciler) yapamamak N-gereksinimlerinden (uygulamalardan) daha fazlasını barındırır, yani bekleme süresine girmeyen müşteriler başka bir yerde hizmet almaya zorlanır. M/M/1/N sistemi. Son olarak, hizmet isteklerini üreten kaynak sınırsız (sonsuz büyük) bir kapasiteye sahiptir. Bu durumda QS durum grafiği, Şekil 3'te gösterilen forma sahiptir.

Şekil 3. Bekleyen tek kanallı bir QS'nin durum grafiği (ölüm ve üreme şeması)

QS durumlarının aşağıdaki yorumu vardır:

S 0 - "kanal boş";

S 1 - "kanal meşgul" (sıra yok);

S 2 - "kanal meşgul" (bir uygulama sırada);

S n - "kanal meşgul" (n -1 uygulama sırada);

S N - "kanal meşgul" (N - 1 başvuru sırada).

Bu sistemdeki durağan süreç, aşağıdaki cebirsel denklem sistemi ile açıklanacaktır:

burada p=yük faktörü

n - durum numarası.

QS modelimiz için yukarıdaki denklem sisteminin çözümü şu şekildedir:

Sınırlı kuyruk uzunluğuna sahip bir QS için olasılığın başlangıç ​​değeri

Sonsuz kuyruğa sahip bir QS için H =? :

P 0 \u003d 1- sn (3.4.7)

Bu QS için durağanlık koşulunun yerine getirilmesinin gerekli olmadığına dikkat edilmelidir, çünkü hizmet sistemine kabul edilen başvuru sayısı, giriş akışının yoğunlukları arasındaki oranla, yani c = l/m oranıyla değil, (N - 1)'i geçemeyen kuyruk uzunluğuna bir kısıtlama getirilerek kontrol edilir.

Yukarıda ele alınan ve sınırsız kuyruğa sahip tek kanallı sistemin aksine, bu durumda, yük faktörü c'nin herhangi bir sonlu değeri için talep sayısının sabit dağılımı mevcuttur.

Bekleyen ve (N - 1) (M/M/1/N)'ye eşit sınırlı kuyruk uzunluğuna sahip tek kanallı bir QS'nin yanı sıra sınırsız kapasiteli arabelleğe (M/M/1/?) sahip tek kanallı bir QS'nin özelliklerini belirleyelim. Sonsuz kuyruğa sahip bir QS için, koşul<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) başvuruya hizmet vermeyi reddetme olasılığı:

İsteklerin kaybedilebildiği sistemlerin en önemli özelliklerinden biri keyfi bir isteğin kaybedilme olasılığı P kaybıdır. Bu durumda, keyfi bir talebi kaybetme olasılığı, keyfi bir anda tüm bekleme yerlerinin dolu olma olasılığı ile örtüşür, yani. k \u003d PH'dan P formülü geçerlidir

2) sistemin göreli verimi:

CMO için sınırsızinci sıra q=1,Çünkü tüm uygulamalar sunulacak

3) mutlak bant genişliği:

4) sistemdeki ortalama başvuru sayısı:

Sınırsız kuyruğa sahip L S

5) Bir başvurunun sistemde ortalama kalma süresi:

Sınırsız sıra için

6) müşterinin (uygulamanın) kuyrukta kaldığı ortalama süre:

Sınırsız sıra ile

7) kuyruktaki ortalama uygulama (müşteri) sayısı (kuyruk uzunluğu):

sınırsız sıra ile

Sıradaki ortalama bekleme süresi T pt ve ortalama kuyruk uzunluğu L pt formülünün yanı sıra isteklerin sistemdeki ortalama kalma süresi T S ve sistemdeki ortalama istek sayısı L ​​S ile ilgili ifadeleri karşılaştırdığımızda, görüyoruz ki

L och \u003d l * T och Ls \u003d l * T s

Bu formüllerin, incelenmekte olan M/A/1 sisteminden daha genel birçok kuyruk sistemi için de geçerli olduğuna ve Little formülleri olarak adlandırıldığına dikkat edin. Bu formüllerin pratik önemi, L och ve L s değerlerinin bilinen bir değeri ile T och ve T s değerlerini doğrudan hesaplama ihtiyacını ortadan kaldırmaları ve bunun tersi gerçeğinde yatmaktadır.

Tek kanal için görevler CMObeklenti ile, İlebeklenti vesınırlı kuyruk uzunluğu

1. Sınırsız kuyruk toplayıcı ile tek satırlık bir QS verildi. Uygulamalar her t =14 saniyede bir gelir. Bir mesajın ortalama iletim süresi t=10 saniyedir. Servis veren kanalın meşgul olduğu saatlerde gelen mesajlar servis başlayana kadar kuyruğa alınmadan kuyruğa alınır.

Aşağıdaki performans göstergelerini belirleyin:

2. Bir kanalı ve m=3 bekleyen mesaj (N-1=m) için bir kuyruk sürücüsü olan düğümler arası iletişim dalı, n=5 mesaj oranıyla en basit mesaj akışını alır. saniye olarak.. Mesaj iletim süresi üstel kanuna göre dağıtılır. Bir mesajın ortalama iletim süresi 0,1 saniyedir. Hizmet veren kanalın daha önce alınan bir mesajı iletmekle meşgul olduğu ve sürücüde boş alan olmadığı zamanlarda gelen mesajlar reddedilir.

Р otk - mesaj alamama olasılığı

L syst - kuyrukta bulunan ve iletişim dalı boyunca iletilen ortalama toplam mesaj sayısı

T och - iletim başlamadan önce mesajın kuyrukta kaldığı ortalama süre

T syst - sistemde bir mesajın harcadığı ortalama toplam süre, kuyrukta ortalama bekleme süresi ve ortalama iletim süresinin toplamı

Q- göreli bant genişliği

A mutlak verimdir

3. Bir kanala ve m = 4 (N-1=4) bekleyen mesaj için bir kuyruk deposuna sahip olan ikincil iletişim ağının düğümler arası şubesi, saniyede = 8 mesaj oranıyla en basit mesaj akışını alır. Mesaj iletim süresi üstel olarak dağıtılır. Bir mesaj için ortalama iletim süresi t = 0,1 saniyedir. Hizmet veren kanalın daha önce alınan bir mesajı iletmekle meşgul olduğu ve sürücüde boş alan olmadığı zamanlarda gelen mesajlar kuyrukta reddedilir.

P otk - düğümler arası şubenin iletişim kanalı üzerinden iletilmek üzere bir mesaj alamama olasılığı;

L och - sıranın ikincil ağının iletişim dalına giden kuyruktaki ortalama mesaj sayısı;

L syst - kuyruktaki ve ikincil ağın iletişim dalı aracılığıyla iletilen ortalama toplam mesaj sayısı;

T och - iletim başlamadan önce mesajın kuyrukta kaldığı ortalama süre;

Р zan - iletişim kanalının doluluk olasılığı (nispi kanal yükü katsayısı);

Q, düğümler arası dalın göreli kapasitesidir;

A, düğümler arası dalın mutlak kapasitesidir;

4. Bir kanala ve m=2 bekleyen mesaj için bir kuyruk sürücüsüne sahip olan düğümler arası iletişim dalı, n=4 mesaj yoğunluğuyla en basit mesaj akışını alır. saniye olarak.. Mesaj iletim süresi üstel kanuna göre dağıtılır. Bir mesajın ortalama iletim süresi 0,1 saniyedir. Hizmet veren kanalın daha önce alınan bir mesajı iletmekle meşgul olduğu ve sürücüde boş alan olmadığı zamanlarda gelen mesajlar reddedilir.

İletişim şubesinin aşağıdaki performans göstergelerini belirleyin:

Р otk - mesaj alamama olasılığı

L och - iletişim şubesine kuyruktaki ortalama mesaj sayısı

L syst - kuyrukta bulunan ve iletişim dalı boyunca iletilen ortalama toplam mesaj sayısı

T och - iletim başlamadan önce mesajın kuyrukta kaldığı ortalama süre

T syst - sistemde bir mesajın harcadığı ortalama toplam süre, kuyrukta ortalama bekleme süresi ve ortalama iletim süresinin toplamı

Р zan - iletişim kanalının doluluk olasılığı (bağıl kanal yükünün katsayısı c)

Q- göreli bant genişliği

A mutlak verimdir

5. İkincil iletişim ağının bir kanalı ve sınırsız bir bekleyen mesaj saklama kuyruğu olan düğümler arası şubesi, saniyede n = 0,06 mesaj yoğunluğuyla en basit mesaj akışını alır. Bir mesajın ortalama iletim süresi t = 10 saniye. İletişim kanalının meşgul olduğu zamanlarda gelen mesajlar kuyruğa alınır ve servis başlayana kadar oradan ayrılmaz.

İkincil ağın iletişim kolunun aşağıdaki performans göstergelerini belirleyin:

L och - iletişim şubesine kuyruktaki ortalama mesaj sayısı;

L syst - kuyruktaki ve iletişim dalı boyunca iletilen ortalama toplam mesaj sayısı;

T och - kuyrukta bir ileti tarafından harcanan ortalama süre;

T syst, kuyruktaki ortalama bekleme süresi ile ortalama iletim süresinin toplamı olan bir iletinin sistemde harcadığı ortalama toplam süredir;

Р zan - iletişim kanalının doluluk olasılığı (kanalın bağıl yük katsayısı);

Q, düğümler arası dalın göreli kapasitesidir;

A - düğümler arası dalın mutlak verimi

6. Sınırsız kuyruk toplayıcı ile tek satırlık bir QS verildi. Uygulamalar her t =13 saniyede bir gelir. Mesaj başına ortalama iletim süresi

t=10 saniye. Servis veren kanalın meşgul olduğu saatlerde gelen mesajlar servis başlayana kadar kuyruğa alınmadan kuyruğa alınır.

Aşağıdaki performans göstergelerini belirleyin:

L och - kuyruktaki ortalama mesaj sayısı

L syst - kuyrukta bulunan ve iletişim dalı boyunca iletilen ortalama toplam mesaj sayısı

T och - iletim başlamadan önce mesajın kuyrukta kaldığı ortalama süre

T syst - sistemde bir mesajın harcadığı ortalama toplam süre, kuyrukta ortalama bekleme süresi ve ortalama iletim süresinin toplamı

Р zan - doluluk olasılığı (bağıl kanal yükünün katsayısı c)

Q- göreli bant genişliği

A mutlak verimdir

7. Özel bir teşhis gönderisi, tek kanallı bir QS'dir. Teşhis için bekleyen araçlar için park yeri sayısı sınırlıdır ve 3'e eşittir [(N - 1) = 3]. Tüm otoparklar doluysa, yani sırada zaten üç araba varsa, teşhis için gelen bir sonraki araba servis kuyruğuna girmez. Teşhis için gelen arabaların akışı Poisson yasasına göre dağıtılır ve yoğunluğu = 0,85'tir (saatte araba). Araba teşhis süresi üstel kanuna göre dağıtılır ve ortalama 1,05 saate eşittir.

Durağan modda çalışan diyagnostik postun olasılıksal özelliklerini belirlemek gerekir: P 0 , P 1 , P 2 , P 3 , P 4 , P open, q, A, L och, L sys, T och, T sis

ETKİNLİK 4

Bekleme, bekleme ve sınırlı kuyruk uzunluğu ile çok kanallı QS

Beklemeli çok kanallı bir kuyruk sistemi düşünün. Bu tür QS, genellikle bir çevrimiçi modda çalışan LAN abone terminallerinin gruplarını modellerken kullanılır. Sıralama süreci aşağıdakilerle karakterize edilir: giriş ve çıkış akışları sırasıyla yoğunluklara sahip Poisson'dur ve; paralel olarak en fazla n istemciye hizmet verilebilir. Sistemde n servis kanalı vardır. İstemci başına ortalama hizmet süresi, her kanal için 1/dak'dır. Bu sistem aynı zamanda ölüm ve üreme sürecini de ifade eder.

с=l/nm - gelen akış yoğunluğunun toplam hizmet yoğunluğuna oranı, sistem yük faktörüdür

(İle<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

burada Р 0, sınırsız kuyruğa sahip tüm kanalların serbest olma olasılığıdır, k, uygulama sayısıdır.

c=l/m kabul edersek, sınırsız bir sıra için P 0 belirlenebilir:

Sınırlı sıra için:

burada m, sıranın uzunluğudur

Sınırsız sıra ile:

Bağıl verim q=1,

Mutlak bant genişliği A \u003d l,

Ortalama dolu kanal sayısı Z=A/m

Sınırlı sıra ile

1 İkincil iletişim ağının düğümler arası dalında n = 4 kanal vardır. İletişim kolunun kanalları üzerinden iletilmek üzere gelen mesajların akışının hızı = saniyede 8 mesajdır. Her bir iletişim kanalı tarafından bir mesajın iletilmesi için ortalama süre t = 0,1, t/n = 0,025 saniyedir. Sıradaki mesajların bekleme süresi sınırsızdır. CMO özelliklerini bulun:

R otk - mesajların iletilmemesi olasılığı;

Q, iletişim dalının göreli verimidir;

A, iletişim dalının mutlak verimidir;

Z, ortalama meşgul kanal sayısıdır;

L och - sıradaki ortalama mesaj sayısı;

T exp - ortalama bekleme süresi;

T syst - kuyruktaki mesajların ve iletişim şubesi boyunca iletimin harcadığı ortalama toplam süre.

2. Tesisin üç direkli (kanallı) mekanik atölyesi, küçük ölçekli mekanizasyonun onarımlarını gerçekleştirir. Atölyeye gelen arızalı mekanizmaların akışı Poisson'dur ve günde = 2,5 mekanizma yoğunluğuna sahiptir, bir mekanizmanın ortalama onarım süresi üstel kanuna göre dağıtılır ve = 0,5 güne eşittir. Diyelim ki fabrikada başka atölye yok ve bu nedenle atölyenin önündeki mekanizma kuyruğu neredeyse sonsuza kadar uzayabilir. Sistemin olasılıksal özelliklerinin aşağıdaki sınır değerlerinin hesaplanması gerekmektedir:

Sistem durumlarının olasılıkları;

Hizmet kuyruğundaki ortalama uygulama sayısı;

Sistemdeki ortalama uygulama sayısı;

Başvurunun kuyruktaki ortalama süresi;

Bir uygulamanın sistemde ortalama kalış süresi.

3. İkincil iletişim ağının düğümler arası şubesi n=3 kanala sahiptir. İletişim kolunun kanalları aracılığıyla iletilmek üzere gelen mesajların akışı saniyede n=5 mesaj yoğunluğuna sahiptir. Bir mesajın ortalama iletim süresi t=0,1 , t/n=0,033 saniyedir Bekleyen mesaj kuyruk sürücüsünde m= 2 mesaja kadar saklanabilir. Sıradaki tüm yerlerin dolu olduğu bir zamanda gelen bir mesaj, iletişim dalında bir iletim reddi alır. QS'nin özelliklerini bulun: Р ref, mesaj iletim hatası olasılığı, Q göreli verim, A mutlak verim, Z meşgul kanalların ortalama sayısı, L och kuyruktaki ortalama mesaj sayısı, T exp ortalama bekleme süresi, T sys mesajın kuyrukta kaldığı ortalama toplam süre ve iletişim kolu boyunca iletimi.

ETKİNLİK 5

Kapalı QS

Kapalı kuyruk sisteminin bir modeli olan makine parkına hizmet verme modelini ele alalım. Şimdiye kadar, yalnızca gelen talep akışının yoğunluğunun sistemin durumuna bağlı olmadığı kuyruk sistemlerini ele aldık. Bu durumda, taleplerin kaynağı QS'nin dışındadır ve sınırsız bir talep akışı oluşturur. Sistemin durumuna bağlı olan, gereksinimlerin kaynağının dahili olduğu ve sınırlı bir istek akışı oluşturduğu kuyruk sistemlerini düşünün. Örneğin, N makineden oluşan bir makine parkına R teknisyenden oluşan bir ekip (N > R) hizmet vermektedir ve her makineye yalnızca bir teknisyen hizmet verebilmektedir. Burada makineler gereksinimlerin (hizmet talepleri) kaynaklarıdır ve mekanikler hizmet kanallarıdır. Servis sonrası arızalanan bir makine, amaçlanan amacı için kullanılır ve potansiyel bir servis gereksinimleri kaynağı haline gelir. Açıkçası, yoğunluk şu anda kaç arabanın çalışır durumda olduğuna (N - k) ve kaç arabanın bakıma alındığına veya hizmet için sırada beklediğine (k) bağlıdır. Ele alınan modelde, gereksinimlerin kaynağının kapasitesinin sınırlı olduğu düşünülmelidir. Gelen gereksinim akışı, rastgele zamanlarda arızalanan ve bakım gerektiren, çalışmakta olan (N - k) sınırlı sayıda makineden gelir. Ayrıca (N - k)'den her makine çalışıyor. Diğer nesnelerden bağımsız olarak X yoğunluğuna sahip bir Poisson talep akışı oluşturur, toplam gelen akışın yoğunluğu vardır. En az bir kanalın boş olduğu anda sisteme giren bir talep anında servise gönderilir. Bir gereksinim, tüm kanalları diğer gereksinimlere hizmet vermekle meşgul bulursa, sistemden ayrılmaz, ancak sıraya girer ve kanallardan biri boş olana kadar bekler. Böylece kapalı bir kuyruk sisteminde, gelen ihtiyaç akışı gidenden oluşur. Sistemin durumu S k, hizmet verilen ve kuyrukta k'ye eşit toplam istek sayısı ile karakterize edilir. Ele alınan kapalı sistem için, açıkça, k = 0, 1, 2, ... , N. Ayrıca, sistem S k durumundaysa, o zaman çalışan nesnelerin sayısı (N - k) olur. Eğer - makine başına gereksinim akışının yoğunluğu, o zaman:

Kapalı bir QS'nin sabit bir modda çalışmasını açıklayan cebirsel denklem sistemi aşağıdaki gibidir:

Bu sistemi çözerek k'inci durumun olasılığını buluyoruz:

P 0 değeri, P k , k = 0, 1, 2, ... , N formülleriyle elde edilen sonuçların normalleştirilmesi koşulundan belirlenir. Sistemin aşağıdaki olasılıksal özelliklerini tanımlayalım:

Hizmet kuyruğundaki ortalama istek sayısı:

Sistemdeki ortalama istek sayısı (hizmette ve kuyrukta)

ortalama tamirci (kanal) sayısı iş eksikliği nedeniyle "boşta"

Kuyruktaki hizmet verilen nesnenin (makine) kesinti oranı

Nesnelerin (makinelerin) kullanım oranı

Hizmet kanallarının kesinti oranı (mekanik)

Servis için ortalama bekleme süresi (kuyrukta servis için bekleme süresi)

Kapalı QS sorunu

1. Aynı üretkenliğe sahip iki mühendisin on kişisel bilgisayara (PC) hizmet vermesine izin verin. Bir bilgisayarın arıza (arıza) akışı, yoğunluk = 0,2 olan Poisson'dur. Bir PC'nin hizmet süresi üstel bir yasaya uyar. Bir PC'nin bir mühendis tarafından ortalama bakım süresi: = 1,25 saat. Aşağıdaki servis organizasyonu seçenekleri mevcuttur:

Her iki mühendis de on bilgisayarın hepsine hizmet eder, bu nedenle PC arızalanırsa, serbest mühendislerden biri ona hizmet eder, bu durumda R = 2, N = 10;

İki mühendisin her biri kendisine atanmış beş PC'ye sahiptir. Bu durumda, R = 1, N = 5.

PC bakımını organize etmek için en iyi seçeneği seçmek gereklidir.

P k: P 1 - P 10 durumlarının tüm olasılıklarını tanımlamak gerekir, bu göz önüne alındığında ve P k hesaplamasının sonuçlarını kullanarak P 0'ı hesaplıyoruz.

ETKİNLİK 6

Trafik hesabı.

Teletrafik teorisi, kuyruk teorisinin bir bölümüdür. Teletrafik teorisinin temelleri Danimarkalı bilim adamı A.K. Erlang. Eserleri 1909-1928'de yayınlandı. Teletrafik teorisinde (TT) kullanılan önemli tanımları verelim. "Trafik" (İngilizce, trafik) terimi, "telefon yükü" terimine karşılık gelir. QS girişlerine gelen çağrıların, gereksinimlerin, mesajların akışının yarattığı yükü ifade eder. Trafik hacmi, bir veya başka bir kaynak tarafından kaçırılan ve bu kaynağın analiz edilen süre boyunca kullanıldığı toplam, integral zaman aralığının değeri olarak adlandırılır. Bir iş birimi, bir kaynağın ikinci işgali olarak düşünülebilir. Bazen saatlerce, bazen sadece saniyeler veya saatlerce okuyabilirsiniz. Ancak, ITU tavsiyeleri trafik hacminin boyutunu erlango saatlerinde vermektedir. Böyle bir ölçü biriminin anlamını anlamak için bir trafik parametresi daha dikkate alınmalıdır - trafik yoğunluğu. Bu durumda, genellikle belirli bir kaynak havuzundaki (kümedeki) trafiğin (yük) ortalama yoğunluğu hakkında konuşurlar. Belirli bir aralıktaki (t 1 ,t 2) her t anında, bu kümedeki hizmet trafiği tarafından işgal edilen kaynakların sayısı A(t)'ye eşitse, o zaman ortalama trafik yoğunluğu

Trafik yoğunluğunun değeri, belirli bir zaman aralığında trafiğin işgal ettiği ortalama kaynak sayısı olarak karakterize edilir. Yük yoğunluğunun ölçü birimi bir Erlang'dır (1 Erl, 1 E), yani. 1 erlang, bir kaynağın tam olarak kullanılmasını gerektiren veya başka bir deyişle, kaynak tarafından bir saniyelik işin gerçekleştirildiği trafik yoğunluğudur - bir saniyelik bir işgal. Amerikan literatüründe bazen CCS- Centrum (veya yüz) Saniye Çağrısı (hektosaniye meslekler) adı verilen başka bir ölçü birimi bulabilirsiniz. CCS numarası, sunucuların 1 saat içinde 100 saniye aralıklarla dolu olduğu süreyi yansıtır. CCS'de ölçülen yoğunluk, 36CCS=1 Erl formülü kullanılarak Erlangs'a dönüştürülebilir.

Bir kaynak tarafından oluşturulan ve saat-oturum olarak ifade edilen trafik, belirli bir T zaman aralığı için c arama denemesi sayısının ve bir denemenin ortalama süresinin t: y = c t (h-h) ürününe eşittir. Trafik üç farklı şekilde hesaplanabilir:

1) Saatteki c görüşme sayısı 1800 ve ortalama ders süresi t = 3 dakika olsun, Y = 1800 görüşme olsun. /H 0,05 saat = 90 Erl;

2) belirli bir demetin çıktılarının tüm n meşguliyetlerinin ti sürelerinin T süresi boyunca sabitlenmesine izin verin, ardından trafik aşağıdaki gibi belirlenir:

3) T süresi boyunca, belirli bir ışının aynı anda işgal edilen çıkışlarının sayısı üzerinden düzenli aralıklarla gözlem yapılsın, gözlemlerin sonuçlarına göre, x(t) süresinin bir adım fonksiyonu oluşturulur (Şekil 8).

Şekil 8. Aynı anda kullanılan ışın çıkışlarının sayısı

T süresi boyunca trafik, bu süre boyunca x(t)'nin ortalama değeri olarak tahmin edilebilir:

burada n, aynı anda kullanılan çıktıların örnek sayısıdır. Y'nin değeri, T süresi boyunca aynı anda işgal edilen ışın çıkışlarının ortalama sayısıdır.

Trafik dalgalanmaları. İkincil telefon ağlarının trafiği zaman içinde önemli ölçüde dalgalanır. Çalışma günü boyunca, trafik eğrisinin iki hatta üç tepe noktası vardır (Şekil 9).

Şekil 9. Gün içinde trafikteki dalgalanmalar

Uzun süreli trafiğin en belirgin olduğu günün saatine yoğun saat (BUSH) denir. CNN'deki trafik bilgisi, kanalların (hatların) sayısını, istasyonların ve düğümlerin ekipman miktarını belirlediği için temelde önemlidir. Haftanın aynı günü trafikte mevsimsel dalgalanmalar vardır. Haftanın günü tatil öncesi bir günse, bu günün NPV'si tatilden sonraki günden daha yüksektir. Ağ tarafından desteklenen hizmetlerin sayısı artarsa, trafik de artar. Bu nedenle, trafik zirvelerinin meydana gelişini yeterli bir kesinlikle tahmin etmek sorunludur. Trafik, ağ yönetimi ve tasarım kuruluşları tarafından yakından izlenir. Trafik ölçüm kuralları ITU-T tarafından geliştirilmekte ve ulusal şebeke idareleri tarafından hem kendi şebekelerinin hem de ona bağlı diğer şebekelerin abonelerinin hizmet kalitesi gereksinimlerini karşılamak için kullanılmaktadır. Teletrafik teorisi, yalnızca trafik durağansa (istatistiksel olarak sabit) bir istasyonun (düğümün) kayıplarının veya ekipman hacminin pratik hesaplamaları için kullanılabilir. Bu koşul, CNN'deki trafik tarafından yaklaşık olarak karşılanmaktadır. PBX'e günlük alınan yük miktarı, ekipmanların önlenmesini ve onarımını etkiler. Gün boyunca istasyondaki yükün düzensizliği, konsantrasyon katsayısı ile belirlenir.

NNN'nin daha kesin bir tanımı aşağıdaki gibidir. Öneri ITU E.500, 12 aylık yoğunluk verilerinin analiz edilmesini, bunlardan en yoğun 30 günün seçilmesini, bu günlerde en yoğun saatlerin bulunmasını ve bu aralıklar üzerinden yoğunluk ölçüm sonuçlarının ortalamasını öngörür. Bu trafik yoğunluğunun (yükünün) hesaplanması, yoğun saatteki veya A seviyesindeki trafik yoğunluğunun normal tahmini olarak adlandırılır. Seçilen 30 günlük sürenin en yoğun 5 günü üzerinden daha katı bir tahminin ortalaması alınabilir. Böyle bir değerlendirmeye B seviyesinin yükseltilmesi veya değerlendirilmesi denir.

Trafik oluşturma süreci. Telefon şebekesinin her kullanıcısının bildiği gibi, aranan aboneyle bağlantı kurmaya yönelik tüm girişimler başarıyla sonuçlanmaz. Bazen istenen bağlantı kurulmadan önce birkaç başarısız girişimde bulunmanız gerekir.

Şekil 10. Aboneler arasında bir bağlantı kurulduğundaki olayların diyagramı

A ve B aboneleri arasında bir bağlantı kurulmasını simüle ederken olası olayları ele alalım (Şekil 10). Telefon şebekelerindeki aramalara ilişkin istatistiksel veriler şu şekildedir: tamamlanan aramaların payı %70-50, başarısız aramaların payı %30-50'dir. Abonenin herhangi bir girişimi, QS'nin girişini işgal eder. Başarılı denemelerde (konuşma gerçekleştiğinde), girişler ve çıkışlar arasında bağlantı kuran anahtarlama cihazlarının doluluk süresi, başarısız denemelere göre daha uzundur. Abone, bağlantı girişimlerini dilediği zaman kesebilir. Yeniden denemeler aşağıdaki nedenlerden kaynaklanabilir:

Numara yanlış çevrildi;

Ağda bir hata varsayımı;

Konuşmanın aciliyet derecesi;

Başarısız önceki girişimler;

B abonesinin alışkanlıklarını bilmek;

Doğru çevirme konusunda şüphe.

Aşağıdaki koşullara bağlı olarak yeniden deneme denenebilir:

aciliyet dereceleri;

Başarısızlık nedenlerinin tahminleri;

Tekrarlanan girişimlerin uygunluğuna ilişkin tahminler,

Denemeler arasındaki kabul edilebilir aralığın tahminleri.

Yeniden denemeyi reddetme, düşük derecede aciliyetle ilişkilendirilebilir. Aramalar tarafından oluşturulan birkaç trafik türü vardır: gelen (teklif edilen) Y p ve cevapsız Y p. Trafik Y p, tüm başarılı ve başarısız girişimleri içerir, Y p'nin bir parçası olan trafik Y p, başarılı ve başarısız girişimlerin bir bölümünü içerir:

Y pr \u003d Y p + Y np,

burada Y p - konuşma (faydalı) trafik ve Y np - başarısız girişimler tarafından oluşturulan trafik. Eşitlik Y p = Y p, yalnızca ideal durumda, kayıplar, arayanların hataları ve aranan abonelerin yanıtları yoksa mümkündür.

Belirli bir süre için gelen ve kaçırılan yükler arasındaki fark, kayıp yük olacaktır.

Trafik tahmini. Sınırlı kaynaklar, istasyonun ve ağın aşamalı olarak genişletilmesi ihtiyacına yol açar. Ağ yönetimi, aşağıdakileri göz önünde bulundurarak, geliştirme aşamasında trafikte bir artış tahmininde bulunur:

Gelir, geçen trafiğin Yp kısmına göre belirlenir, - maliyetler, en yüksek trafikte hizmet kalitesine göre belirlenir;

Kayıpların büyük bir kısmı (düşük kalite) nadir durumlarda meydana gelir ve geliştirme döneminin sonu için tipiktir;

Kaçırılan trafiğin en büyük hacmi, neredeyse hiç kaybın olmadığı dönemlere düşer - kayıplar% 10'dan azsa, aboneler bunlara yanıt vermez. İstasyonların ve ağın gelişimini planlarken, tasarımcı, hizmet sağlama kalitesi (kayıplar için) için gereklilikler nelerdir sorusunu yanıtlamalıdır. Bunu yapmak için, ülkede kabul edilen kurallara göre trafik kayıplarını ölçmek gerekir.

Bir trafik ölçümü örneği.

Öncelikle, aynı anda bazı trafiğe hizmet eden birkaç kaynağa sahip bir QS'nin çalışmasını nasıl görüntüleyebileceğinizi düşünün. Uygulamaların veya gereksinimlerin akışına hizmet eden sunucular gibi kaynaklardan daha fazla bahsedeceğiz. Bir sunucu havuzu tarafından isteklere hizmet verme sürecini tasvir etmenin en görsel ve yaygın olarak kullanılan yollarından biri Gantt şemasıdır. Bu grafik, apsisi zamanı temsil eden ve ordinatı havuz sunucularına karşılık gelen ayrık noktaları temsil eden dikdörtgen bir koordinat sistemidir. Şekil 11, üç sunuculu bir sistem için bir Gantt şemasını göstermektedir.

İlk üç zaman aralığında (onları bir saniye olarak kabul ediyoruz), birinci ve üçüncü sunucular meşgul, sonraki iki saniye - yalnızca üçüncü, ardından ikinci bir saniye, ardından ikinci ve birinci iki saniye ve son iki saniye - yalnızca birinci.

Oluşturulan diyagram, trafik hacmini ve yoğunluğunu hesaplamanıza olanak tanır. Diyagram, sunucular tarafından sunulamayan isteklerin sisteme girip girmediği hakkında hiçbir şey söylemediğinden, yalnızca sunulan veya kaçırılan trafiği gösterir.

Geçen trafiğin hacmi, Gantt şemasının tüm bölümlerinin toplam uzunluğu olarak hesaplanır. 10 saniyede ses:

Apsis boyunca çizilen her bir zaman aralığıyla ilişkilendirin, bu tek aralıkta kullanılan sunucuların sayısına eşit bir tamsayı. Bu değer A(t) anlık yoğunluktur. Örneğimiz için

A(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Şimdi 10 saniyelik bir süre boyunca ortalama trafik yoğunluğunu bulalım.

Böylece, söz konusu üç sunuculu sistemden geçen trafiğin ortalama yoğunluğu 1,5 Erl'ye eşittir.

Ana yük parametreleri

Telefon iletişimi, aşağıdakilerle karakterize edilen çeşitli abone kategorileri tarafından kullanılır:

yük kaynaklarının sayısı - N,

belirli bir zamanda bir kaynaktan gelen ortalama çağrı sayısı (genellikle HNN) - s,

bir aramaya hizmet verirken anahtarlama sisteminin bir işgalinin ortalama süresi t'dir.

Yük yoğunluğu

Farklı çağrı kaynakları tanımlayalım. Örneğin,

Ofis telefonu başına ofis telefonu başına ortalama arama sayısı;

Bir apartman münferit cihazından gelen ortalama çağrı sayısı; Rastgele olay kuyruğa alma teletrafik

bir sayımla - toplu kullanım için aparattan aynı;

ma ile - bir madeni para makinesinden aynı;

sl ile - bir bağlantı hattından aynı.

O zaman bir kaynaktan gelen ortalama arama sayısı:

İlgili kategorideki bir kaynaktan gelen ortalama arama sayısına ilişkin yaklaşık veriler vardır:

3,5 - 5, \u003d 0,5 - 1, sayımla \u003d 1,5 - 2, ma \u003d 15 - 30 ile, sl \u003d 10 - 30 ile.

Bağlantının sonucuna bağlı olarak istasyonda farklı bir telefon yükü oluşturan aşağıdaki bağlantı türleri vardır:

k p - bir görüşmede sona eren bağlantıların oranını gösteren katsayı;

k c - aranan abonenin meşguliyeti nedeniyle görüşme ile bitmeyen bağlantılar;

k ve - aranan abonenin yanıt vermemesi nedeniyle görüşme ile bitmeyen bağlantıların oranını ifade eden katsayı;

k osh - arayanın hataları nedeniyle görüşmeyle bitmeyen bağlantılar;

k tanesi - teknik nedenlerle bir konuşma ile bitmeyen aramalar.

Ağın normal çalışması sırasında bu katsayıların değerleri şuna eşittir:

k p =0.60-0.75; kc=0.12-0.15; k fakat =0.08-0.12; kosh =0.02-0.05; k bunlar = 0,005-0,01.

Bir dersin ortalama süresi, bağlantı türlerine bağlıdır. Örneğin, bağlantı bir görüşme ile sona erdiyse, cihazların ortalama işgal süresi t durumu şuna eşit olacaktır:

bağlantı kurma süresi nerede;

t koşul - gerçekleşen konuşma;

t in - aranan abonenin telefon setine çağrı gönderme süresi;

t p - konuşmanın süresi

nerede t - yardımcı istasyon yanıt sinyali;

1.5n - aranan abonenin arama süresi (n - numaradaki karakter sayısı);

t ile - mekanizmaları değiştirerek bir bağlantı kurmak ve konuşmanın bitiminden sonra bağlantıyı kesmek için gereken süre. Ele alınan miktarların yaklaşık değerleri:

t co \u003d 3 sn., t c \u003d 1-2.5 sn., t in \u003d 8-10 sn., t p \u003d 90-130 sn.

Görüşmeyle bitmeyen aramalar da telefon yükü oluşturuyor.

Aranan abone meşgul olduğunda cihazların ortalama doluluk süresi eşittir.

burada t ayarlanır. (4.2.3) tarafından belirlenir

t buzzer - meşgul zili dinleme süresi, t zil =6sn.

Aranan abone cevap vermediğinde cihazların ortalama doluluk süresi eşittir

burada t pv, geri arama kontrol sinyalinin dinlenme süresidir, t pv = 20 sn.

Abone hatalarından dolayı görüşme olmadıysa, o zaman ortalama olarak t osh = 30 sn.

Teknik nedenlerle görüşme ile sonlanmayan oturumların süresi, bu tür oturumların yüzdesi az olduğu için tanımlanmamıştır.

Yukarıdakilerin hepsinden, bir grup kaynak tarafından NTT için yaratılan toplam yükün, bireysel meslek türlerinin yüklerinin toplamına eşit olduğu sonucu çıkar.

şartları hisse senedi olarak dikkate alan bir katsayı nerede

Yedi haneli numaralandırmaya sahip bir telefon şebekesinde, abonelerin yapısal bileşimi aşağıdaki gibi olan otomatik bir telefon santrali tasarlandı:

N chr \u003d 4000, N ind \u003d 1000, N sayısı \u003d 2000, N ma \u003d 400, N sl \u003d 400.

Yoğun bir saatte bir kaynaktan gelen ortalama çağrı sayısı

(4.2.3) ve (4.2.6) formüllerine göre yükü buluruz

1.10.62826767 saniye = 785.2 hz.

Y=Nct formülünden ortalama ders süresi t

t= E/Nc= 2826767/7800*3,8=95,4 sn.

Görev yükle

1. Yedi haneli numaralandırmaya sahip bir telefon şebekesinde, abonelerin yapısal bileşimi aşağıdaki gibi olan otomatik bir telefon santrali tasarlanmıştır:

N uchr \u003d 5000, N ind \u003d 1500, N sayısı \u003d 3000, N ma \u003d 500, N sl \u003d 500.

İstasyona gelen yükü belirleyin - Y, ortalama kullanım süresi t, biliniyorsa

uchr \u003d 4 ile, ind \u003d 1 ile, sayma ile \u003d 2, ma \u003d 10 ile, sl \u003d 12 ile, t p \u003d 120 sn., t in \u003d 10 sn., k p \u003d 0.6, t ile \u003d 1 sn., \u 003d 1.1.

Allbest.ru'da barındırılıyor

Benzer Belgeler

Düzgün dağılmış rasgele değişken kavramı. Çarpımsal uyumlu yöntem. Sürekli rastgele değişkenlerin ve ayrık dağılımların modellenmesi. Bir borç veren ve bir borç alan arasındaki ekonomik ilişkilerin simülasyonu için algoritma.

dönem ödevi, 01/03/2011 eklendi


Kuyruk teorisinin genel kavramları. Kuyruk sistemlerinin modellenmesinin özellikleri. QS durum grafikleri, bunları açıklayan denklemler. Model çeşitlerinin genel özellikleri. Süpermarket kuyruk sisteminin analizi.

dönem ödevi, 11/17/2009 eklendi


Kuyruk teorisinin unsurları. Kuyruk sistemlerinin matematiksel modellemesi, sınıflandırılması. Kuyruk sistemlerinin simülasyon modellemesi. Teorinin pratik uygulaması, matematiksel yöntemlerle problem çözme.

dönem ödevi, 05/04/2011 eklendi


Rastgele bir süreç kavramı. Kuyruk teorisinin görevleri. Kuyruk sistemlerinin (QS) sınıflandırılması. Olasılıksal matematiksel model. Rastgele faktörlerin bir nesnenin davranışı üzerindeki etkisi. Beklemeli tek kanallı ve çok kanallı QS.

dönem ödevi, 25.09.2014 tarihinde eklendi


Bir kuyruk sisteminin etkin inşası ve işletilmesinin teorik yönlerinin, ana unsurlarının, sınıflandırılmasının, özelliklerinin ve performansının incelenmesi. GPSS dilinde bir kuyruk sisteminin modellenmesi.

dönem ödevi, 24.09.2010 tarihinde eklendi


Dinamik programlama, ağ planlama ve ürün üretim yönetimi teorisinin geliştirilmesi. Ekonomik süreçlerin modellenmesi problemlerinde oyun teorisinin bileşenleri. Kuyruk teorisinin pratik uygulamasının unsurları.

uygulamalı çalışma, 01/08/2011 eklendi


Rastgele olaylar, nicelikler ve fonksiyonlar hakkında temel kavramlar. Rastgele değişkenlerin sayısal özellikleri. Dağılımların asimetri türleri. Rastgele değişkenlerin dağılımının istatistiksel değerlendirmesi. Yapısal-parametrik tanımlama problemlerini çözme.

dönem ödevi, 03/06/2012 eklendi


Kuyruk sürecinin modellenmesi. Farklı kuyruk kanalları türleri. Arızalı tek kanallı kuyruk modelinin çözümü. Servis Süresi Dağıtım Yoğunluğu. Mutlak verimin tanımı.

testi, 03/15/2016 eklendi


Karayolu taşımacılığı alanında kuyruk sisteminin fonksiyonel özellikleri, yapısı ve ana unsurları. Kuyruk sisteminin işleyişinin kalitesinin nicel göstergeleri, bunların belirlenmesinin prosedürü ve ana aşamaları.

laboratuvar çalışması, 03/11/2011 eklendi


Modelleme hedefinin belirlenmesi. Gerçek nesnelerin tanımlanması. Model tipinin seçimi, matematiksel şema. Sürekli stokastik bir modelin inşası. Kuyruk teorisinin temel kavramları. Olayların akışını tanımlayın. Algoritma bildirimi.