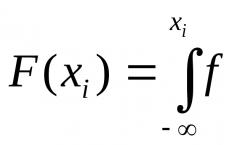Metoda inverzne funkcije

Neka se traži reprodukcija kontinuirane slučajne varijable x, tj. dobiti niz njegovih mogućih vrijednosti x ja (ja= 1,2, ...), poznavajući funkciju distribucije F(x).

Teorema. Ako r ja ,-slučajni broj, zatim moguća vrijednostx ja kontinuirana slučajna varijabla X koja se igra s danom funkcijom distribucijeF(x)odgovarar ja , je korijen jednadžbe

F(x ja)= r ja . (»)

Dokaz. Neka se odabere slučajni broj r ja (0≤r ja <1). Так как в интервале всех возможных зна­чений x distribucijska funkcija F(x) monotono raste od 0 do 1, tada u tom intervalu postoji, i to samo jedna, takva vrijednost argumenta x ja , pri kojoj funkcija raspodjele poprima vrijednost r ja. Drugim riječima, jednadžba (*) ima jedinstveno rješenje

x ja = F - 1 (r ja),

Gdje F - 1 - inverzna funkcija y=F(x).

Dokažimo sada da je korijen x ja jednadžba (*) je moguća vrijednost takve kontinuirane slučajne varijable (privremeno ćemo je označiti sa ξ , a zatim se uvjerite da ξ=X). U tu svrhu dokazujemo da je vjerojatnost pogotka ξ u interval, na primjer ( S,d), koji pripada intervalu svih mogućih vrijednosti x, jednak je prirastu funkcije distribucije F(x) na ovom intervalu:

R(S< ξ < d)= F(d)- F(S).

Doista, budući da F(x)- monotono rastuća funkcija u intervalu svih mogućih vrijednosti x, tada u tom intervalu velike vrijednosti argumenta odgovaraju velikim vrijednostima funkcije i obrnuto. Stoga, ako S <x ja < d, To F(c)< r ja < F(d), i obrnuto [uzimajući u obzir da zbog (*) F(x ja)=r ja ].

Iz ovih nejednakosti slijedi da ako je slučajna varijabla ξ zatvoreno u intervalu

S< ξ < d, ξ (**)

zatim slučajna varijabla R zatvoreno u intervalu

F(S)< R< F(d), (***)

i natrag. Dakle, nejednakosti (**) i (***) su ekvivalentne, a samim tim i jednako vjerojatne:

R(S< ξ< d)=P[F(S)< R< F(d)]. (****)

Budući da vrijednost R ravnomjerno raspoređena u intervalu (0,1), zatim vjerojatnost pogotka R nekom intervalu koji pripada intervalu (0,1) jednaka je njegovoj duljini (vidi poglavlje XI, § 6, napomena). Posebno,

R[F(S)< R< F(d) ] = F(d) - F(S).

Stoga se relacija (****) može napisati kao

R(S< ξ< d)= F(d) - F(S).

Dakle, vjerojatnost pogotka ξ u interval ( S,d) jednak je prirastu funkcije distribucije F(x) na ovom intervalu, što znači da ξ=X. Drugim riječima, brojke x ja, definirane formulom (*), postoje moguće vrijednosti količine X s dana funkcija distribucije F(x), Q.E.D.

Pravilo 1x ja , kontinuirana slučajna varijabla x, poznavajući njegovu distribucijsku funkciju F(x), morate odabrati nasumični broj r ja izjednačiti njegove funkcije distribucije i riješiti x ja , rezultirajuća jednadžba

F(x ja)= r ja .

Napomena 1. Ako se ova jednadžba ne može eksplicitno riješiti, tada se pribjegava grafičkim ili numeričkim metodama.

Primjer I Igrajte 3 moguće vrijednosti kontinuirane slučajne varijable x, ravnomjerno raspoređeni u intervalu (2, 10).

Riješenje. Napišimo funkciju raspodjele količine x, ravnomjerno raspoređen u intervalu ( A,b) (vidi Poglavlje XI, § 3, primjer):

F(x)= (Ha)/ (b-A).

Po uvjetu, a = 2, b=10, dakle,

F(x)= (X- 2)/ 8.

Koristeći pravilo iz ovog odjeljka, pišemo jednadžbu za pronalaženje mogućih vrijednosti x ja , za koju funkciju distribucije izjednačavamo sa slučajnim brojem:

(x ja -2 )/8= r ja .

Odavde x ja =8 r ja + 2.

Odaberimo 3 nasumična broja, na primjer, r ja =0,11, r ja =0,17, r ja=0,66. Zamijenite ove brojeve u jednadžbu, razriješite s obzirom na x ja , kao rezultat toga dobivamo odgovarajuće moguće vrijednosti x: x 1 \u003d 8 0,11 + 2 \u003d\u003d 2,88; x 2 =1.36; x 3 = 7,28.

Primjer 2 Kontinuirana slučajna varijabla x raspodijeljena prema eksponencijalnom zakonu zadanom funkcijom raspodjele (poznat je parametar λ > 0)

F(x)= 1 - e - λ x (x>0).

Potrebno je pronaći eksplicitnu formulu za igranje mogućih vrijednosti x.

Riješenje. Koristeći pravilo ovog odlomka, napišemo jednadžbu

1 - e - λ x ja

Riješimo ovu jednadžbu za x ja :

e - λ x ja = 1 - r ja, ili - λ x ja = ul(1 - r ja).

x ja =1p(1– r ja)/λ .

Slučajni broj r ja unutar intervala (0,1); dakle broj 1 - r ja, također slučajan i pripada intervalu (0,1). Drugim riječima, količine R i 1- R ravnomjerno raspoređeni. Stoga, kako bi pronašli x ja Možete koristiti jednostavniju formulu:

x ja =- ul r ja /λ.

Napomena 2. Poznato je da (vidi Poglavlje XI, §3)

Posebno,

Iz toga slijedi da ako je poznata gustoća vjerojatnosti f(x), zatim igrati x umjesto jednadžbi F(x ja)=r ja odluči x ja jednadžba

Pravilo 2 Da biste pronašli moguću vrijednost x ja (kontinuirana slučajna varijabla x, znajući njegovu gustoću vjerojatnosti f(x) odaberite slučajni broj r ja i odlučiti se x ja , jednadžba

ili jednadžba

Gdje A- najmanja konačna moguća vrijednost x.

Primjer 3 S obzirom na gustoću vjerojatnosti kontinuirane slučajne varijable xf(x)=λ (1-λx/2) u intervalu (0; 2/λ); izvan ovog intervala f(x)= 0. Potrebno je pronaći eksplicitnu formulu za igranje mogućih vrijednosti x.

Riješenje. Zapisujemo u skladu s pravilom 2 jednadžbu

Nakon integriranja i rješavanja dobivene kvadratne jednadžbe za x ja, konačno dobivamo

LABORATORIJSKI RAD MM-03

IGRANJE DISKRETNIH I KONTINUIRANIH ROV-ova

Svrha rada: proučavanje i programska implementacija metoda za reprodukciju diskretnih i kontinuiranih RV

PITANJA ZA PROUČAVANJE IZ SAŽETAKA PREDAVANJA:

1. Diskretne slučajne varijable i njihove karakteristike.

2. Igranje kompletne grupe nasumičnih događaja.

3. Reproduciranje kontinuirane slučajne varijable metodom inverzne funkcije.

4. Izbor slučajnog smjera u prostoru.

5. Standardna normalna razdioba i njezin preračun za zadane parametre.

6. Metoda polarnih koordinata za igranje normalne raspodjele.

ZADATAK 1. Formulirajte (pismeno) pravilo za igranje vrijednosti diskretnog RV, čiji je zakon raspodjele dan u obliku tablice. Sastavite potprogram-funkciju za reprodukciju vrijednosti CV koristeći BSV primljen iz RNG potprograma. Reproducirajte 50 CB vrijednosti i prikažite ih na ekranu.

Gdje je N broj varijante.

ZADATAK 2. Dana je funkcija gustoće distribucije f(x) kontinuirane slučajne varijable X.

U izvješću zapišite formule i izračun sljedećih vrijednosti:

A) konstanta normalizacije;

B) funkcija raspodjele F(x);

C) matematičko očekivanje M(X);

D) disperzija D(X);

E) formula za igranje vrijednosti CB metodom inverzne funkcije.

Sastavite potprogram funkcije za reprodukciju zadanog životopisa i dobivanje 1000 vrijednosti ovog životopisa.

Konstruirajte histogram raspodjele dobivenih brojeva na 20 segmenata.

ZADATAK 3. Napišite postupak koji vam omogućuje reprodukciju parametara slučajnog smjera u prostoru. Igrajte 100 nasumičnih smjerova u prostoru.

Koristite ugrađeni generator pseudoslučajnih brojeva.

Pisano izvješće o laboratorijskom radu treba sadržavati:

1) Naziv i svrha rada, grupa, prezime i broj opcije studenta;

2) Za svaki zadatak: -uvjet, -potrebne formule i matematičke transformacije, -naziv programske datoteke koja implementira korišteni algoritam, -rezultati izračuna.

Otklonjene programske datoteke predaju se zajedno s pisanim izvješćem.

PRIMJENA

Varijante gustoće distribucije kontinuiranog SW

Var-t	Gustoća distribucije SW	Var-t	Gustoća distribucije SW

Suština Monte Carlo metode je sljedeća: trebate pronaći vrijednost A neka vrijednost koja se proučava. U tu svrhu odabire se takva slučajna varijabla X čije je matematičko očekivanje jednako a: M(X)=a.

U praksi, oni rade ovo: izračunavaju (izigravaju) n moguće vrijednosti x i slučajne varijable X, pronaći njihovu aritmetičku sredinu

I uzimaju kao procjenu (približnu vrijednost) a * željenog broja a. Dakle, za primjenu Monte Carlo metode potrebno je znati odigrati slučajnu varijablu.

Neka se traži igranje diskretne slučajne varijable X, tj. izračunajte slijed njegovih mogućih vrijednosti x i (i=1,2, …), poznavajući zakon raspodjele X. Uvedimo oznaku: R je kontinuirana slučajna varijabla ravnomjerno raspoređena u intervalu (0,1); r i (j=1,2,…) – slučajni brojevi (moguće vrijednosti R).

Pravilo: Da bismo odigrali diskretnu slučajnu varijablu X zadanu zakonom distribucije

X x 1 x 2 ... x n

P p 1 p 2 … p n

1. Razdvojite interval (0,1) osi ili na n parcijalnih intervala:

Δ 1 = (0; p 1), Δ 2 = (p 1; p 1+ p 2), ..., Δ n = (p 1 + p 2 + ... + p n -1; 1).

2. Odaberite slučajni broj r j . Ako je r j pao u parcijalni interval Δ i , tada je odigrana vrijednost poprimila moguću vrijednost x i . .

Reprodukcija cijele grupe događaja

Potrebno je igrati testove, u svakom od kojih se dogodi jedan od događaja pune grupe, čije su vjerojatnosti poznate. Igranje kompletne grupe događaja svodi se na igranje diskretne slučajne varijable.

Pravilo: Da bi se odigrali testovi u kojima se dogodi jedan od događaja A 1, A 2, ..., A n pune grupe, čije su vjerojatnosti p 1, p 2, ..., p n poznate, dovoljno je odigrati diskretnu vrijednost X sa sljedećim zakonom raspodjele:

P p 1 p 2 … p n

Ako je u testu vrijednost X poprimila moguću vrijednost x i =i, dogodio se događaj A i.

Igranje kontinuirane slučajne varijable

Poznata je funkcija distribucije F kontinuirane slučajne varijable X. Potrebno je igrati X, tj. izračunati niz mogućih vrijednosti x i (i=1,2, …).

A. Metoda inverznih funkcija. Pravilo 1 x i kontinuirane slučajne varijable X, poznavajući njenu funkciju distribucije F, trebate odabrati slučajni broj r i , izjednačiti njegovu funkciju distribucije i riješiti za x i dobivenu jednadžbu F(h i) = r i .

Ako je poznata gustoća vjerojatnosti f(x), tada se koristi pravilo 2.

Pravilo 2 Odigrati moguće značenje x i kontinuirane slučajne varijable X, znajući njenu gustoću vjerojatnosti f, trebate odabrati slučajni broj r i i riješiti jednadžbu za x i

ili jednadžba

gdje je a najmanja konačna moguća vrijednost X.

B. Metoda superpozicije. Pravilo 3 Kako bi se odigrala moguća vrijednost slučajne varijable X, čija je funkcija distribucije

F(x) = C 1 F 1 (x)+C 2 F 2 (x)+…+C n F n (x),

gdje su F k (x) – funkcije distribucije (k=1, 2, …, n), S k >0, S i +S 2 +…+S n =1, potrebno je odabrati dva neovisna slučajna broja r 1 i r 2 i pomoću slučajnog broja r 1 odigrati moguću vrijednost pomoćne diskretne slučajne varijable Z (prema pravilu 1):

p C 1 C 2 … C n

Ako se pokaže da je Z=k, tada je jednadžba F k (x) = r 2 riješena za x.

Napomena 1. Ako je gustoća vjerojatnosti kontinuirane slučajne varijable X dana u obliku

f(x)=C 1 f 1 (x)+C 2 f 2 (x)+…+C n f n (x),

gdje su f k gustoće vjerojatnosti, koeficijenti C k su pozitivni, njihov zbroj je jednak jedan, a ako se pokaže da je Z=k, tada rješavaju (prema pravilu 2) u odnosu na x i u odnosu na ili jednadžbu

Približno igranje normalne slučajne varijable

Pravilo. Kako bi se približno odredila moguća vrijednost x i normalne slučajne varijable X s parametrima a=0 i σ=1, dodajte 12 neovisnih slučajnih brojeva i oduzmite 6 od dobivene sume:

Komentar. Ako želite približno igrati normalnu slučajnu varijablu Z s matematičkim očekivanjem A i standardne devijacije σ, zatim, odigravši moguću vrijednost x i prema gornjem pravilu, pronalaze željenu moguću vrijednost formulom: z i =σx i +a.

Definicija 24.1.slučajni brojevi imenovati moguće vrijednosti r kontinuirana slučajna varijabla R, ravnomjerno raspoređen u intervalu (0; 1).

1. Igranje diskretne slučajne varijable.

Neka se zahtijeva igranje diskretne slučajne varijable x, odnosno dobiti niz njegovih mogućih vrijednosti, poznavajući zakon distribucije x:

x x 1 x 2 … x n

p str 1 R 2 … r str .

Razmotrimo slučajnu varijablu jednoliko raspodijeljenu u (0, 1) R i podijelite interval (0, 1) na točke s koordinatama R 1, R 1 + R 2 , …, R 1 + R 2 +… +r str-1 uključeno P parcijalnih intervala čije su duljine jednake vjerojatnostima s istim indeksima.

Teorem 24.1. Ako se svakom slučajnom broju koji padne u interval dodijeli moguća vrijednost, tada će odigrana vrijednost imati zadani zakon distribucije:

x x 1 x 2 … x n

p str 1 R 2 … r str .

Dokaz.

Moguće vrijednosti dobivene slučajne varijable podudaraju se sa skupom x 1 , x 2 ,… x n, budući da je broj intervala P, a kada je pogođen r j u intervalu slučajna varijabla može poprimiti samo jednu od vrijednosti x 1 , x 2 ,… x n.

Jer R ravnomjerno raspoređen, tada je vjerojatnost njegovog pada u svaki interval jednaka njegovoj duljini, što implicira da svaka vrijednost odgovara vjerojatnosti pi. Dakle, slučajna varijabla koja se igra ima zadani zakon distribucije.

Primjer. Igrajte 10 vrijednosti diskretne slučajne varijable x, čiji zakon raspodjele ima oblik: x 2 3 6 8

R 0,1 0,3 0,5 0,1

Riješenje. Razdvojimo interval (0, 1) na parcijalne intervale: D 1 - (0; 0,1), D 2 - (0,1; 0,4), D 3 - (0,4; 0,9), D 4 - (0,9; 1). Ispišimo 10 brojeva iz tablice slučajnih brojeva: 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0,34. Prvi i sedmi broj leže na intervalu D 1 , stoga je u tim slučajevima slučajna varijabla koja se igra poprimila vrijednost x 1 = 2; treći, četvrti, osmi i deseti broj pali su u interval D 2 , što odgovara x 2 = 3; drugi, peti, šesti i deveti broj bili su u intervalu D 3 - dok X = x 3 = 6; niti jedan broj nije pao u zadnji interval. Dakle, odigrane moguće vrijednosti x su: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. Igranje suprotnih događaja.

Neka je potrebno igrati suđenja, u svakom od njih događaj A pojavljuje s poznatom vjerojatnošću R. Razmotrimo diskretnu slučajnu varijablu x, koji uzima vrijednosti 1 (ako je događaj A dogodilo) s vjerojatnošću R i 0 (ako A nije se dogodilo) s vjerojatnošću q = 1 – str. Zatim igramo ovu slučajnu varijablu kao što je predloženo u prethodnom paragrafu.

Primjer. Igrajte 10 izazova, svaki s događajem A pojavljuje se s vjerojatnošću od 0,3.

Riješenje. Za slučajnu varijablu x sa zakonom distribucije x 1 0

R 0,3 0,7

dobivamo intervale D 1 - (0; 0,3) i D 2 - (0,3; 1). Koristimo isti uzorak slučajnih brojeva kao u prethodnom primjeru, za koji brojevi №№1,3 i 7 spadaju u interval D 1, a ostatak - u interval D 2 . Stoga možemo pretpostaviti da je događaj A dogodilo u prvom, trećem i sedmom pokušaju, ali se nije dogodilo u ostalima.

3. Igranje kompletne grupe događaja.

Ako događaji A 1 , A 2 , …, A str, čije su vjerojatnosti jednake R 1 , R 2 ,… r str, formirajte kompletnu grupu, a zatim za igranje (to jest, modeliranje slijeda njihovog pojavljivanja u nizu testova), možete igrati diskretnu slučajnu varijablu x sa zakonom distribucije x 1 2 … P,čineći to na isti način kao u stavku 1. Pritom pretpostavljamo da

p str 1 R 2 … r str

Ako x poprima vrijednost x i = i, onda se u ovom suđenju dogodio događaj A i.

4. Igranje kontinuirane slučajne varijable.

a) Metoda inverznih funkcija.

Neka se traži reprodukcija kontinuirane slučajne varijable x, tj. dobiti niz njegovih mogućih vrijednosti x i (ja = 1, 2, …, n), poznavajući funkciju distribucije F(x).

Teorem 24.2. Ako r i je slučajni broj, a zatim moguća vrijednost x i reproducirana kontinuirana slučajna varijabla x sa zadanom funkcijom distribucije F(x), odgovara r i, korijen je jednadžbe

F(x i) = r i. (24.1)

Dokaz.

Jer F(x) monotono raste u rasponu od 0 do 1, tada postoji (i jedinstvena) vrijednost argumenta x i, pri čemu funkcija raspodjele poprima vrijednost r i. Dakle, jednadžba (24.1) ima jedinstveno rješenje: x i= F -1 (r i), Gdje F-1 - funkcija inverzna F. Dokažimo da je korijen jednadžbe (24.1) moguća vrijednost razmatrane slučajne varijable X. Pretpostavimo prvo da x i je moguća vrijednost neke slučajne varijable x, a dokazujemo da je vjerojatnost da x padne u interval ( c, d) jednako je F(d) – F(c). Dapače, zbog monotonosti F(x) i to F(x i) = r i. Zatim

Dakle, vjerojatnost da x padne u interval ( c, d) jednak je prirastu funkcije distribucije F(x) na ovom intervalu, stoga je x = x.

Igrajte 3 moguće vrijednosti kontinuirane slučajne varijable x, ravnomjerno raspoređene u intervalu (5; 8).

F(x) = , odnosno potrebno je riješiti jednadžbu Odaberimo 3 slučajna broja: 0,23; 0,09 i 0,56 i zamijenite ih u ovu jednadžbu. Dobiti odgovarajuće moguće vrijednosti x:

b) Metoda superpozicije.

Ako se funkcija distribucije slučajne varijable koja se igra može prikazati kao linearna kombinacija dviju funkcija distribucije:

tada , jer na x®¥ F(x) ® 1.

Uvodimo pomoćnu diskretnu slučajnu varijablu Z sa zakonom distribucije

Z 12 . Odaberimo 2 neovisna slučajna broja r 1 i r 2 i odigrajte moguće

PC 1 C 2

značenje Z po broju r 1. (vidi stavak 1.). Ako Z= 1, tada tražimo željenu moguću vrijednost x iz jednadžbe, a ako Z= 2, tada rješavamo jednadžbu .

Može se dokazati da je u ovom slučaju funkcija distribucije slučajne varijable koja se igra jednaka danoj funkciji distribucije.

c) Približna simulacija normalne slučajne varijable.

Od R, jednoliko raspodijeljen u (0, 1), , zatim za zbroj P nezavisne, jednoliko raspoređene u intervalu (0,1) slučajne varijable . Zatim, temeljem teorema središnje granice, normalizirana slučajna varijabla na P® ¥ će imati distribuciju blisku normalnoj, s parametrima A= 0 i s =1. Konkretno, dobiva se prilično dobra aproksimacija za P = 12:

Dakle, igrati moguću vrijednost normalizirane normalne slučajne varijable x, morate dodati 12 neovisnih nasumičnih brojeva i oduzeti 6 od zbroja.

Pošaljite svoj dobar rad u bazu znanja jednostavno je. Koristite obrazac u nastavku

Studenti, diplomanti, mladi znanstvenici koji koriste bazu znanja u svom studiju i radu bit će vam vrlo zahvalni.

Domaćin na http://www.allbest.ru/

AKTIVNOST 1

Simulacija slučajnih događaja sa zadanim zakonom raspodjele

Igranje diskretne slučajne varijable

Neka se zahtijeva igranje diskretne slučajne varijable, tj. dobiti niz njegovih mogućih vrijednosti x i (i = 1,2,3,...n), poznavajući zakon distribucije X:

Označimo s R kontinuiranu slučajnu varijablu. Vrijednost R je jednoliko raspoređena u intervalu (0,1). Označimo s r j (j = 1,2,...) moguće vrijednosti slučajne varijable R. Podijelimo interval 0< R < 1 на оси 0r точками с координатами на n частичных интервалов.

Tada dobivamo:

Vidi se da je duljina parcijalnog intervala s indeksom i jednaka vjerojatnosti R s istim indeksom. Duljina

Dakle, kada slučajni broj r i padne u interval, slučajna varijabla X poprima vrijednost x i s vjerojatnošću P i .

Postoji sljedeći teorem:

Ako se svakom slučajnom broju koji je pao u interval dodijeli moguća vrijednost x i , tada će odigrana vrijednost imati zadani zakon distribucije

Algoritam za igranje diskretne slučajne varijable zadane zakonom distribucije

1. Potrebno je interval (0,1) 0r osi razbiti na n parcijalnih intervala:

2. Odaberite (na primjer, iz tablice slučajnih brojeva, ili u računalu) slučajni broj r j .

Ako je r j pao u interval, tada je diskretna slučajna varijabla koja se igra poprimila moguću vrijednost x i .

Igranje kontinuirane slučajne varijable

Neka se traži reprodukcija kontinuirane slučajne varijable X, tj. dobiti niz njegovih mogućih vrijednosti x i (i = 1,2,...). U ovom slučaju poznata je funkcija distribucije F(X).

postoji Sljedeći teorema.

Ako je r i slučajni broj, tada je moguća vrijednost x i reproducirane kontinuirane slučajne varijable X s poznatom funkcijom raspodjele F(X) koja odgovara r i korijen jednadžbe.

Algoritam za reprodukciju kontinuirane slučajne varijable:

1. Potrebno je izabrati slučajni broj r i .

2. Izjednačiti odabrani slučajni broj poznate funkcije distribucije F(X) i dobiti jednadžbu.

3. Riješite ovu jednadžbu za x i . Rezultirajuća vrijednost x i će istovremeno odgovarati slučajnom broju r i . i dat zakon distribucije F(X).

Primjer. Igrajte 3 moguće vrijednosti kontinuirane slučajne varijable X ravnomjerno raspoređene u intervalu (2; 10).

Funkcija distribucije X ima sljedeći oblik:

Prema uvjetu, a = 2, b = 10, dakle,

U skladu s algoritmom za igranje kontinuirane slučajne varijable, izjednačavamo F(X) s odabranim slučajnim brojem r i .. Iz ovoga dobivamo:

Zamijenite ove brojeve u jednadžbu (5.3). Dobivamo odgovarajuće moguće vrijednosti x:

Problemi modeliranja slučajnih događaja sa zadanim zakonom raspodjele

1. Potrebno je odigrati 10 vrijednosti diskretne slučajne varijable, tj. dobiti niz njegovih mogućih vrijednosti x i (i=1,2,3,…n), poznavajući zakon distribucije X

Izaberimo iz tablice slučajnih brojeva slučajni broj r j: 0,10; 0,12; 0,37; 0,09; 0,65; 0,66; 0,99; 0,19; 0,88; 0,59; 0,78

2. Učestalost zaprimanja zahtjeva za uslugu podliježe eksponencijalnom zakonu raspodjele () , x, parametar l je poznat (u daljnjem tekstu l = 1/t je intenzitet zaprimanja zahtjeva)

l=0,5 aplikacija/sat. Odredite slijed vrijednosti za trajanje intervala između prijema zahtjeva. Broj realizacija jednak je 5. Broj r j: 0,10; 0,12; 0,37; 0,09; 0,65; 0,99;

AKTIVNOST 2

Sustav čekanja

Sustavi u kojima s jedne strane postoje masovni zahtjevi za obavljanjem bilo koje vrste usluga, a s druge strane se tim zahtjevima udovoljava nazivamo sustavima čekanja. Svaki QS služi za ispunjavanje toka aplikacija.

QS uključuje: izvor zahtjeva, dolazni tok, red čekanja, servisni uređaj, odlazni tok zahtjeva.

SMO se dijele na:

QS s gubicima (kvarovima)

CMO s čekanjem (neograničena duljina čekanja)

QS s ograničenom duljinom čekanja

CMO s ograničenim vremenom čekanja.

Prema broju kanala odnosno uslužnih uređaja QS su jednokanalni i višekanalni.

Prema mjestu izvora zahtjeva: otvoreni i zatvoreni.

Po broju uslužnih elemenata po potrebi: jednofazni i višefazni.

Jedan od oblika klasifikacije je klasifikacija D. Kendalla - A / B / X / Y / Z

A - određuje raspodjelu vremena između dolazaka;

B - određuje raspodjelu vremena službe;

X - određuje broj servisnih kanala;

Y - određuje propusnost sustava (duljina čekanja);

Z - određuje redoslijed službe.

Kada je kapacitet sustava beskonačan i redoslijed usluge je prvi došao prvi poslužen, Y/Z dijelovi su izostavljeni. Prva znamenka (A) koristi sljedeće znakove:

M-distribucija ima eksponencijalni zakon,

G - nepostojanje bilo kakvih pretpostavki o uslužnom procesu ili se identificira simbolom GI, što znači ponavljajući servisni proces,

D- deterministički (vrijeme usluge je fiksno),

E n - Erlangian n-tog reda,

NM n - hipererlangijan n-tog reda.

Druga znamenka (B) koristi iste simbole.

Četvrta znamenka (Y) pokazuje kapacitet međuspremnika, tj. najveći broj mjesta u redu čekanja.

Peta znamenka (Z) označava način odabira iz reda u sustavu čekanja: SP-equiprobable, FF-first in-first out, LF-last in-first out, PR-priority.

Za zadatke:

l - prosječan broj pristiglih prijava u jedinici vremena

µ je prosječan broj zahtjeva posluženih po jedinici vremena

Faktor opterećenja kanala 1 ili postotak vremena u kojem je kanal zauzet.

Glavne karakteristike:

1) P ref - vjerojatnost kvara - vjerojatnost da će sustav odbiti uslugu i zahtjev je izgubljen. To se događa kada su kanal ili svi kanali zauzeti (PSTN).

Za višekanalni QS R otk = R n, gdje je n broj uslužnih kanala.

Za QS s ograničenom duljinom čekanja R otk =R n + l, gdje je l dopuštena duljina čekanja.

2) Relativna q i apsolutna A propusnost sustava

q \u003d 1-P otk A \u003d ql

3) Ukupan broj zahtjeva u sustavu

L sys = n - za QS s neuspjesima, n je broj kanala koje usluga zauzima.

Za QS s čekanjem i ograničenom duljinom čekanja

L sys \u003d n + L cool

gdje je L exp prosječan broj zahtjeva koji čekaju da servis počne, itd.

Preostale karakteristike ćemo razmotriti u tijeku rješavanja problema.

Jednokanalni i višekanalni sustavi čekanja. Sustavi kvarova.

Najjednostavniji jednokanalni model s probabilističkim ulaznim tokom i servisnom procedurom je model karakteriziran eksponencijalnom distribucijom trajanja intervala između pristizanja zahtjeva i trajanja servisiranja. U ovom slučaju gustoća distribucije trajanja intervala između pristizanja potraživanja ima oblik

Gustoća distribucije trajanja usluge:

Tokovi zahtjeva i usluga su najjednostavniji. Neka sustav radi s kvarovima. Ovaj tip QS-a može se koristiti u modeliranju prijenosnih kanala u lokalnim mrežama. Potrebno je odrediti apsolutnu i relativnu propusnost sustava. Predstavimo ovaj sustav čekanja kao graf (slika 2), koji ima dva stanja:

S 0 - kanal je slobodan (na čekanju);

S 1 - kanal je zauzet (zahtjev se servisira).

Slika 2. Grafikon stanja jednokanalnog QS-a s kvarovima

Označimo vjerojatnosti stanja: P 0 (t) - vjerojatnost stanja "kanal je slobodan"; P 1 (t) - vjerojatnost stanja "kanal je zauzet". Na temelju označenog grafa stanja sastavljamo sustav Kolmogorovih diferencijalnih jednadžbi za vjerojatnosti stanja:

Sustav linearnih diferencijalnih jednadžbi ima rješenje pod uvjetom normalizacije P 0 (t) + P 1 (t) = 1 . Rješenje ovog sustava naziva se nestacionarnim, jer izravno ovisi o t i izgleda ovako:

P 1 (t) = 1 - P 0 (t) (3.4.3)

Lako je vidjeti da za jednokanalni QS s kvarovima, vjerojatnost P 0 (t) nije ništa drugo nego relativni kapacitet sustava q. Doista, P 0 je vjerojatnost da je u trenutku t kanal slobodan i da će zahtjev koji je stigao u trenutku t biti servisiran, pa je, prema tome, za dano vrijeme t, prosječni omjer broja servisiranih zahtjeva prema broju dolaznih zahtjeva također jednak P 0 (t), tj. q = P 0 (t).

Nakon dugog vremenskog intervala (at), postiže se stacionarni (steady-state) režim:

Poznavajući relativnu propusnost, lako je pronaći apsolutnu. Apsolutna propusnost (A) - prosječan broj aplikacija koje sustav čekanja može poslužiti po jedinici vremena:

Vjerojatnost odbijanja servisiranja zahtjeva bit će jednaka vjerojatnosti stanja "kanal je zauzet":

Ova vrijednost P otk može se tumačiti kao prosječni udio neusluženih zahtjeva među onima koji su podneseni.

U velikoj većini slučajeva, u praksi, sustavi čekanja su višekanalni, pa su stoga modeli s n kanala za posluživanje (gdje je n>1) od nedvojbenog interesa. Proces čekanja opisan ovim modelom karakterizira intenzitet ulaznog toka l, dok se paralelno ne može opsluživati ​​više od n klijenata (zahtjeva). Prosječno vrijeme usluge za jedan zahtjev je 1/m. Ulazni i izlazni tok su Poissonovi. Način rada jednog ili drugog uslužnog kanala ne utječe na način rada ostalih uslužnih kanala sustava, a trajanje servisne procedure za svaki od kanala je slučajna varijabla podložna eksponencijalnom zakonu distribucije. Krajnji cilj korištenja n uslužnih kanala povezanih paralelno je povećanje (u usporedbi s jednokanalnim sustavom) brzine servisiranja zahtjeva uslužujući n klijenata istovremeno. Graf stanja višekanalnog sustava čekanja s kvarovima ima oblik prikazan na slici 4.

Slika 4. Grafikon stanja višekanalnog QS-a s kvarovima

S 0 - svi kanali su besplatni;

S 1 - jedan kanal je zauzet, ostali su slobodni;

S k - točno k kanala je zauzeto, ostali su slobodni;

S n - svih n kanala je zauzeto, ostali su slobodni.

Kolmogorovljeve jednadžbe za vjerojatnosti stanja sustava P 0 , ... ,P k , ... P n imat će sljedeći oblik:

Početni uvjeti za rješavanje sustava su sljedeći:

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0 .

Stacionarno rješenje sustava ima oblik:

Formule za izračunavanje vjerojatnosti P k (3.5.1) nazivaju se Erlangove formule.

Odredimo vjerojatnostne karakteristike funkcioniranja višekanalnog QS-a s kvarovima u stacionarnom načinu rada:

1) vjerojatnost kvara:

budući da se zahtjev odbija ako stigne u trenutku kada je svih n kanala zauzeto. Vrijednost P otk karakterizira potpunost usluge dolaznog toka;

2) vjerojatnost da će aplikacija biti prihvaćena za uslugu (to je također relativna propusnost sustava q) dopunjuje P otk do jedinice:

3) apsolutna propusnost

4) prosječan broj kanala koje zauzima usluga () je sljedeći:

Vrijednost karakterizira stupanj opterećenja QS-a.

Zadacina lekciju 2

1. Komunikacijska grana, koja ima jedan kanal, prima najjednostavniji tok poruka intenziteta n = 0,08 poruka u sekundi. Vrijeme prijenosa je raspoređeno prema zakonu exp. Servisiranje jedne poruke odvija se s intenzitetom µ=0,1. Poruke koje stižu u trenucima kada je kanal za posluživanje zauzet odašiljanjem prethodno primljene poruke dobivaju grešku u prijenosu.

Coeff. Relativno opterećenje kanala (vjerojatnost da je kanal zauzet)

P

Q je relativni kapacitet internodalne grane

I apsolutna propusnost komunikacijske grane.

2. Komunikacijska grana ima jedan kanal i prima poruke svakih 10 sekundi. Vrijeme usluge za jednu poruku je 5 sekundi. Vrijeme prijenosa poruke raspoređeno je eksponencijalno. Poruke koje stižu u vrijeme kada je kanal zauzet uskraćuju se.

Definirati

R zan - vjerojatnost popunjenosti komunikacijskog kanala (faktor relativnog opterećenja)

Q- relativna propusnost

A je apsolutna propusnost komunikacijske grane

4. Internodalna grana sekundarne komunikacijske mreže ima n = 4 kanala. Protok poruka koje pristižu na prijenos preko kanala komunikacijske grane ima brzinu = 8 poruka u sekundi. Prosječno vrijeme prijenosa jedne poruke je t = 0,1 sekunda.Poruka koja stigne u trenutku kada je svih n kanala zauzeto dobiva grešku u prijenosu duž komunikacijske grane. Pronađite CMO karakteristike:

AKTIVNOST 3

Jednokanalni sustav s čekanjem

Razmotrimo sada jednokanalni QS s očekivanjem. Sustav čekanja ima jedan kanal. Dolazni tijek servisnih zahtjeva je najjednostavniji tok s intenzitetom. Intenzitet protoka usluge je jednak (tj. u prosjeku će kontinuirano zauzet kanal izdati servisirane zahtjeve). Trajanje usluge je slučajna varijabla podložna eksponencijalnom zakonu raspodjele. Tok usluge je najjednostavniji Poissonov tok događaja. Zahtjev koji stigne u vrijeme kada je kanal zauzet nalazi se u redu i čeka uslugu. Ovaj QS je najčešći u modeliranju. Uz jedan ili drugi stupanj aproksimacije, može se koristiti za simulaciju gotovo bilo kojeg čvora lokalne mreže (LAN).

Pretpostavimo da bez obzira na to koliko zahtjeva uđe u ulaz sustava za posluživanje, ovaj sustav (red čekanja + usluženi klijenti) Ne možete zadovoljiti više od N-zahtjeva (prijava), tj. klijenti koji ne uđu u razdoblje čekanja prisiljeni su biti usluženi negdje drugdje. M/M/1/N sustav. Konačno, izvor koji generira servisne zahtjeve ima neograničen (beskonačno velik) kapacitet. QS graf stanja u ovom slučaju ima oblik prikazan na slici 3

Slika 3. Grafikon stanja jednokanalnog QS-a s čekanjem (shema smrti i reprodukcije)

QS stanja imaju sljedeću interpretaciju:

S 0 - "kanal je slobodan";

S 1 - "kanal je zauzet" (nema čekanja);

S 2 - "kanal je zauzet" (jedna aplikacija je u redu čekanja);

S n - "kanal je zauzet" (n -1 aplikacija je u redu);

S N - "kanal je zauzet" (N - 1 aplikacija je u redu čekanja).

Stacionarni proces u ovom sustavu opisat će se sljedećim sustavom algebarskih jednadžbi:

gdje je p=faktor opterećenja

n - državni broj.

Rješenje gornjeg sustava jednadžbi za naš QS model ima oblik:

Početna vrijednost vjerojatnosti za QS s ograničenom duljinom čekanja

Za QS s beskonačnim redom H =? :

P 0 \u003d 1- s (3.4.7)

Treba napomenuti da ispunjenje uvjeta stacionarnosti za ovaj QS nije potrebno, jer se broj prijava primljenih u sustav za posluživanje kontrolira uvođenjem ograničenja na duljinu reda čekanja, koje ne smije biti veće od (N - 1), a ne omjerom intenziteta ulaznog toka, odnosno ne omjerom c = l/m.

Za razliku od jednokanalnog sustava, koji je razmatran gore i s neograničenim redom čekanja, u ovom slučaju postoji stacionarna distribucija broja zahtjeva za bilo koje konačne vrijednosti faktora opterećenja c.

Odredimo karakteristike jednokanalnog QS-a s čekanjem i ograničenom duljinom reda jednakim (N - 1) (M/M/1/N), kao i za jednokanalni QS s međuspremnikom neograničenog kapaciteta (M/M/1/?). Za QS s beskonačnim redom čekanja, uvjet s<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) vjerojatnost odbijanja usluge aplikacije:

Jedna od najvažnijih karakteristika sustava u kojima se zahtjevi mogu izgubiti je vjerojatnost P gubitak da će proizvoljni zahtjev biti izgubljen. U tom slučaju vjerojatnost gubitka proizvoljnog zahtjeva podudara se s vjerojatnošću da su u proizvoljnom trenutku sva mjesta čekanja zauzeta, tj. vrijedi formula P iz k \u003d P H

2) relativna propusnost sustava:

Za CMO s neograničenimred čekanja q=1, jer sve prijave će biti uslužene

3) apsolutna propusnost:

4) prosječan broj prijava u sustavu:

L S s neograničenim redom

5) prosječno vrijeme zadržavanja aplikacije u sustavu:

Za neograničen red

6) prosječno trajanje boravka klijenta (aplikacije) u redu čekanja:

S neograničenim redom

7) prosječan broj prijava (klijenata) u redu čekanja (duljina čekanja):

s neograničenim redom čekanja

Uspoređujući izraze za prosječno vrijeme čekanja u redu čekanja T pt i formulu za prosječnu duljinu reda čekanja L pt, kao i prosječno vrijeme zadržavanja zahtjeva u sustavu T S i prosječni broj zahtjeva u sustavu L S , vidimo da

L och \u003d l * T och L s \u003d l * T s

Imajte na umu da ove formule također vrijede za mnoge sustave čekanja općenitije od sustava M/M/1 koji se razmatra i zovu se Littleove formule. Praktični značaj ovih formula leži u činjenici da eliminiraju potrebu za izravnim izračunavanjem vrijednosti T och i T s s poznatom vrijednošću vrijednosti L och i L s i obrnuto.

Zadaci za jednokanalni CMOs očekivanjem, Siščekivanje iograničena duljina čekanja

1. Zadan jednolinijski QS s neograničenim akumulatorom čekanja. Prijave stižu svakih t =14 sekundi. Prosječno vrijeme prijenosa jedne poruke je t=10 sekundi. Poruke koje stižu u vrijeme kada je kanal za posluživanje zauzet primaju se u red čekanja bez napuštanja iz njega dok usluga ne počne.

Odredite sljedeće pokazatelje učinka:

2. Internodalna grana komunikacije, koja ima jedan kanal i pogon u redu čekanja za m=3 poruke na čekanju (N-1=m), prima najjednostavniji tok poruka s brzinom od n=5 poruka. u sek.. Vrijeme prijenosa poruke raspoređeno je po eksponencijalnom zakonu. Prosječno vrijeme prijenosa jedne poruke je 0,1 sekunda. Poruke koje stižu u trenucima kada je kanal za posluživanje zauzet odašiljanjem prethodno primljene poruke i kada nema slobodnog prostora na disku se odbijaju.

R otk - vjerojatnost neuspjeha primanja poruke

L syst - prosječan ukupan broj poruka u redu i prenesenih duž komunikacijske grane

T och - prosječno vrijeme koje poruka ostaje u redu čekanja prije početka prijenosa

T syst - prosječno ukupno vrijeme koje poruka provede u sustavu, zbroj prosječnog vremena čekanja u redu čekanja i prosječnog vremena prijenosa

Q- relativna propusnost

A je apsolutna propusnost

3. Internodalna grana sekundarne komunikacijske mreže, koja ima jedan kanal i pogon u redu čekanja za m = 4 (N-1=4) poruke na čekanju, prima najjednostavniji protok poruka s brzinom od = 8 poruka u sekundi. Vrijeme prijenosa poruke raspoređeno je eksponencijalno. Prosječno vrijeme prijenosa jedne poruke je t = 0,1 sekunda. Poruke koje stižu u trenucima kada je kanal za posluživanje zauzet odašiljanjem prethodno primljene poruke i kada nema slobodnog prostora na disku odbijaju se u redu čekanja.

P otk - vjerojatnost neuspjeha primanja poruke za prijenos preko komunikacijskog kanala internodalne grane;

L och - prosječan broj poruka u redu do komunikacijske grane sekundarne mreže reda;

L syst - prosječan ukupan broj poruka u redu i prenesenih kroz komunikacijsku granu sekundarne mreže;

T och - prosječno vrijeme koje poruka ostaje u redu čekanja prije početka prijenosa;

R zan - vjerojatnost popunjenosti komunikacijskog kanala (koeficijent relativnog opterećenja kanala);

Q je relativni kapacitet internodalne grane;

A je apsolutni kapacitet internodalne grane;

4. Internodalna komunikacijska grana, koja ima jedan kanal i pogon u redu čekanja za m=2 poruke na čekanju, prima najjednostavniji protok poruka s intenzitetom od n=4 poruke. u sek.. Vrijeme prijenosa poruke raspoređeno je po eksponencijalnom zakonu. Prosječno vrijeme prijenosa jedne poruke je 0,1 sekunda. Poruke koje stižu u trenucima kada je kanal za posluživanje zauzet odašiljanjem prethodno primljene poruke i kada nema slobodnog prostora na disku se odbijaju.

Odredite sljedeće pokazatelje uspješnosti komunikacijske grane:

R otk - vjerojatnost neuspjeha primanja poruke

L och - prosječan broj poruka u redu do komunikacijske grane

L syst - prosječan ukupan broj poruka u redu i prenesenih duž komunikacijske grane

T och - prosječno vrijeme koje poruka ostaje u redu čekanja prije početka prijenosa

T syst - prosječno ukupno vrijeme koje poruka provede u sustavu, zbroj prosječnog vremena čekanja u redu čekanja i prosječnog vremena prijenosa

R zan - vjerojatnost popunjenosti komunikacijskog kanala (koeficijent relativnog opterećenja kanala c)

Q- relativna propusnost

A je apsolutna propusnost

5. Internodalna grana sekundarne komunikacijske mreže, koja ima jedan kanal i neograničeni red čekanja poruka, prima najjednostavniji tok poruka intenziteta n = 0,06 poruka u sekundi. Prosječno vrijeme prijenosa jedne poruke t =10 sekundi. Poruke koje stižu u vrijeme kada je komunikacijski kanal zauzet primaju se u red čekanja i ne napuštaju ga do početka usluge.

Odredite sljedeće pokazatelje učinkovitosti komunikacijske grane sekundarne mreže:

L och - prosječan broj poruka u redu do komunikacijske grane;

L syst - prosječan ukupan broj poruka u redu i prenesenih duž komunikacijske grane;

T och - prosječno vrijeme koje poruka provede u redu čekanja;

T syst je prosječno ukupno vrijeme koje poruka provede u sustavu, što je zbroj prosječnog vremena čekanja u redu i prosječnog vremena prijenosa;

R zan - vjerojatnost popunjenosti komunikacijskog kanala (koeficijent relativnog opterećenja kanala);

Q je relativni kapacitet internodalne grane;

A - apsolutna propusna moć internodalne grane

6. Zadan jednolinijski QS s neograničenim akumulatorom čekanja. Prijave stižu svakih t =13 sekundi. Prosječno vrijeme prijenosa po poruci

t=10 sekundi. Poruke koje stižu u vrijeme kada je kanal za posluživanje zauzet primaju se u red čekanja bez napuštanja iz njega dok usluga ne počne.

Odredite sljedeće pokazatelje učinka:

L och - prosječan broj poruka u redu čekanja

L syst - prosječan ukupan broj poruka u redu i prenesenih duž komunikacijske grane

T och - prosječno vrijeme koje poruka ostaje u redu čekanja prije početka prijenosa

T syst - prosječno ukupno vrijeme koje poruka provede u sustavu, zbroj prosječnog vremena čekanja u redu čekanja i prosječnog vremena prijenosa

R zan - vjerojatnost popunjenosti (koeficijent relativnog opterećenja kanala c)

Q- relativna propusnost

A je apsolutna propusnost

7. Specijalizirani dijagnostički post je jednokanalni QS. Broj parkirališnih mjesta za automobile koji čekaju na dijagnostiku je ograničen i iznosi 3 [(N - 1) = 3]. Ako su sva parkirna mjesta zauzeta, odnosno već su tri automobila u redu, tada sljedeći automobil koji je stigao na dijagnostiku ne ulazi u servisni red. Protok automobila koji dolaze na dijagnostiku raspoređen je prema Poissonovom zakonu i ima intenzitet = 0,85 (automobila na sat). Vrijeme autodijagnostike raspoređeno je po eksponencijalnom zakonu i u prosjeku iznosi 1,05 sati.

Potrebno je odrediti vjerojatnosne karakteristike dijagnostičkog mjesta koje radi u stacionarnom načinu rada: P 0 , P 1 , P 2 , P 3 , P 4 , P otvoreno, q, A, L och, L sys, T och, T sis

AKTIVNOST 4

Višekanalni QS s čekanjem, s čekanjem i ograničenom duljinom čekanja

Razmotrimo višekanalni sustav čekanja s čekanjem. Ovaj tip QS-a često se koristi pri modeliranju grupa LAN pretplatničkih terminala koji rade u on-line načinu rada. Proces čekanja karakterizira sljedeće: ulazni i izlazni tokovi su Poissonovi s intenzitetima i respektivno; ne više od n klijenata može biti opsluženo paralelno. Sustav ima n servisnih kanala. Prosječno vrijeme usluge po klijentu je 1/m za svaki kanal. Ovaj sustav također se odnosi na proces smrti i reprodukcije.

s=l/nm - omjer intenziteta dolaznog protoka prema ukupnom intenzitetu usluge, je faktor opterećenja sustava

(S<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

gdje je R 0 vjerojatnost slobodnog stanja svih kanala s neograničenim redom čekanja, k je broj prijava.

ako prihvatimo c=l / m, tada se P 0 može odrediti za neograničeni red:

Za ograničeni red:

gdje je m duljina reda čekanja

S neograničenim redom:

Relativna propusnost q=1,

Apsolutna širina pojasa A \u003d l,

Prosječan broj zauzetih kanala Z=A/m

S ograničenim redom

1 Međučvorna grana sekundarne komunikacijske mreže ima n = 4 kanala. Protok poruka koje pristižu na prijenos preko kanala komunikacijske grane ima brzinu = 8 poruka u sekundi. Prosječno vrijeme t = 0,1 za prijenos jedne poruke po svakom komunikacijskom kanalu je t/n = 0,025 sekundi. Vrijeme čekanja za poruke u redu čekanja je neograničeno. Pronađite CMO karakteristike:

R otk - vjerojatnost neuspjeha prijenosa poruka;

Q je relativna propusnost komunikacijske grane;

A je apsolutna propusnost komunikacijske grane;

Z je prosječan broj zauzetih kanala;

L och - prosječan broj poruka u redu čekanja;

T exp - prosječno vrijeme čekanja;

T syst - prosječno ukupno vrijeme provedeno porukama u redu i prijenosu duž komunikacijske grane.

2. Mehanička radionica pogona sa tri stupa (kanala) obavlja popravke male mehanizacije. Tok neispravnih mehanizama koji pristižu u radionicu je Poissonov i ima intenzitet = 2,5 mehanizama dnevno, prosječno vrijeme popravka jednog mehanizma je raspoređeno po eksponencijalnom zakonu i jednako je = 0,5 dana. Pretpostavimo da u tvornici nema druge radionice, pa stoga red mehanizama ispred radionice može rasti gotovo unedogled. Potrebno je izračunati sljedeće granične vrijednosti vjerojatnosnih karakteristika sustava:

Vjerojatnosti stanja sustava;

Prosječan broj aplikacija u servisnom redu;

Prosječan broj aplikacija u sustavu;

Prosječno trajanje prijave u redu čekanja;

Prosječno trajanje boravka aplikacije u sustavu.

3. Internodalna grana sekundarne komunikacijske mreže ima n=3 kanala. Tok poruka koje pristižu na prijenos kroz kanale komunikacijske grane ima intenzitet od n=5 poruka u sekundi. Prosječno vrijeme prijenosa jedne poruke je t=0,1, t/n=0,033 s. Do m= 2 poruke mogu se pohraniti u pogon čekanja poruka. Poruka koja stigne u trenutku kada su sva mjesta u redu čekanja zauzeta dobiva odbijenicu prijenosa na komunikacijskoj grani. Nađite karakteristike QS-a: R ref je vjerojatnost neuspjeha prijenosa poruke, Q je relativna propusnost, A je apsolutna propusnost, Z je prosječan broj zauzetih kanala, L och je prosječan broj poruka u redu čekanja, T exp je prosječno vrijeme čekanja, T sys je prosječno ukupno vrijeme boravka poruke u redu čekanja i njenog prijenosa duž komunikacijske grane.

AKTIVNOST 5

Zatvoren QS

Razmotrimo model opsluživanja strojnog parka, koji je model zatvorenog sustava čekanja. Do sada smo razmatrali samo takve sustave čekanja za koje intenzitet dolaznog toka zahtjeva ne ovisi o stanju sustava. U ovom slučaju, izvor zahtjeva je izvan QS-a i generira neograničen protok zahtjeva. Razmotrite sustave čekanja za koje ovisi o stanju sustava, gdje je izvor zahtjeva interni i generira ograničen protok zahtjeva. Na primjer, strojni park koji se sastoji od N strojeva održava tim od R mehaničara (N > R), a svaki stroj može servisirati samo jedan mehaničar. Ovdje su strojevi izvori zahtjeva (zahtjeva za servisiranjem), a mehaničari su servisni kanali. Pokvareni stroj nakon servisa koristi se za namjeravanu svrhu i postaje potencijalni izvor servisnih zahtjeva. Očito, intenzitet ovisi o tome koliko je automobila trenutno u pogonu (N - k) i koliko je automobila na servisu ili čeka na servis (k). U modelu koji se razmatra, kapacitet izvora zahtjeva treba smatrati ograničenim. Dolazni tok zahtjeva dolazi od ograničenog broja strojeva u radu (N - k), koji u nasumičnim trenucima zakažu i zahtijevaju održavanje. Štoviše, svaki stroj iz (N - k) radi. Generira Poissonov tok potražnje s intenzitetom X bez obzira na druge objekte, ukupni dolazni tok ima intenzitet. Zahtjev koji uđe u sustav u trenutku kada je barem jedan kanal slobodan odmah se šalje na servis. Ako zahtjev utvrdi da su svi kanali zauzeti služenjem drugim zahtjevima, tada ne napušta sustav, već stoji u redu i čeka dok se jedan od kanala ne oslobodi. Dakle, u zatvorenom sustavu čekanja, dolazni tok zahtjeva formira se od odlaznog. Stanje S k sustava karakterizira ukupni broj zahtjeva koji se servisiraju iu redu čekanja, jednak k. Za zatvoreni sustav koji razmatramo, očito, k = 0, 1, 2, ... , N. Štoviše, ako je sustav u stanju S k, tada je broj objekata u radu (N - k). Ako je - intenzitet protoka zahtjeva po stroju, tada:

Sustav algebarskih jednadžbi koji opisuje rad zatvorene QS u stacionarnom načinu rada je sljedeći:

Rješavajući ovaj sustav, nalazimo vjerojatnost k-tog stanja:

Vrijednost P 0 određena je iz uvjeta normalizacije rezultata dobivenih formulama za P k , k = 0, 1, 2, ... , N. Definirajmo sljedeće vjerojatnosne karakteristike sustava:

Prosječan broj zahtjeva u servisnom redu:

Prosječan broj zahtjeva u sustavu (u servisu i u redu čekanja)

prosječan broj mehaničara (kanala) "miruju" zbog nedostatka posla

Omjer zastoja servisiranog objekta (stroja) u redu čekanja

Stopa iskorištenja objekata (strojeva)

Omjer zastoja servisnih kanala (mehanika)

Prosječno vrijeme čekanja na uslugu (vrijeme čekanja na uslugu u redu čekanja)

Zatvoreni QS problem

1. Neka dva inženjera iste produktivnosti budu zadužena za servisiranje deset osobnih računala (PC). Tok kvarova (kvarova) jednog računala je Poisson s intenzitetom = 0,2. Vrijeme servisiranja osobnog računala slijedi eksponencijalni zakon. Prosječno vrijeme održavanja jednog računala od strane jednog inženjera je: = 1,25 sati. Dostupne su sljedeće mogućnosti organizacije usluga:

Oba inženjera opslužuju svih deset računala, pa ako PC zakaže, jedan od slobodnih inženjera ga opslužuje, u ovom slučaju R = 2, N = 10;

Svaki od dva inženjera održava pet računala koja su mu dodijeljena. U ovom slučaju, R = 1, N = 5.

Potrebno je odabrati najbolju opciju za organizaciju održavanja računala.

Potrebno je definirati sve vjerojatnosti stanja P k: P 1 - P 10, s obzirom da i korištenjem rezultata izračuna P k izračunavamo P 0

AKTIVNOST 6

Proračun prometa.

Teorija teleprometa dio je teorije čekanja u redu. Temelje teorije teleprometa postavio je danski znanstvenik A.K. Erlang. Radovi su mu objavljeni 1909.-1928. Navedimo važne definicije koje se koriste u teoriji teleprometa (TT). Pojam "promet" (engleski, traffic) odgovara pojmu "telefonsko opterećenje". Podrazumijeva opterećenje koje stvara protok poziva, zahtjeva, poruka koje stižu na ulaze QS-a. Opseg prometa naziva se vrijednost ukupnog, integralnog vremenskog intervala koji je propustio jedan ili drugi resurs, tijekom kojeg je ovaj resurs bio zauzet za analizirano vremensko razdoblje. Jedinica rada može se smatrati drugom zauzetošću resursa. Ponekad možete čitati o satima, a ponekad samo o sekundama ili satima. Međutim, preporuke ITU-a daju dimenziju opsega prometa u erlango satima. Za razumijevanje značenja takve mjerne jedinice potrebno je uzeti u obzir još jedan prometni parametar - intenzitet prometa. U ovom slučaju često se govori o prosječnom intenzitetu prometa (opterećenju) na određenom skupu (skupu) resursa. Ako je u svakom trenutku vremena t iz zadanog intervala (t 1 ,t 2) broj resursa iz tog skupa zauzetih opsluživanjem prometa jednak A(t), tada će prosječni intenzitet prometa biti

Vrijednost intenziteta prometa karakterizira se kao prosječan broj resursa zauzetih za opsluživanje prometa u određenom vremenskom intervalu. Mjerna jedinica intenziteta opterećenja je jedan Erlang (1 Erl, 1 E), tj. 1 erlang je količina prometa koja zahtijeva punu uposlenost jednog resursa, odnosno, drugim riječima, pri kojoj rad od jedne sekunde obavlja resurs - okupacija za vrijeme od jedne sekunde. U američkoj literaturi ponekad možete pronaći još jednu mjernu jedinicu pod nazivom CCS- Centrum (ili stotinu) Calls Second (hektosekunda zanimanja). CCS broj odražava vrijeme zauzetosti poslužitelja u intervalima od 100 sekundi u 1 satu. Intenzitet izmjeren u CCS može se pretvoriti u Erlangs pomoću formule 36CCS=1 Erl.

Promet koji generira jedan izvor i izražen u satima-sesijama jednak je umnošku broja pokušaja poziva c za određeni vremenski interval T i prosječnog trajanja jednog pokušaja t: y = c t (h-h). Promet se može izračunati na tri različita načina:

1) neka je broj poziva c po satu 1800, a prosječno trajanje sata t = 3 minute, tada je Y = 1800 poziva. /h 0,05 h = 90 Erl;

2) neka su trajanja t i svih n zauzetosti izlaza određenog snopa fiksna tijekom vremena T, tada se promet određuje na sljedeći način:

3) neka se tijekom vremena T motrenje provodi u pravilnim intervalima preko broja istovremeno zauzetih izlaza određene grede, prema rezultatima promatranja gradi se stepenasta funkcija vremena x(t) (slika 8).

Slika 8. Brojevi simultano okupiranih izlaza snopa

Promet tijekom vremena T može se procijeniti kao prosječna vrijednost x(t) tijekom ovog vremena:

gdje je n broj uzoraka simultano okupiranih izlaza. Vrijednost Y je prosječan broj simultano okupiranih izlaza snopa tijekom vremena T.

Prometne fluktuacije. Promet sekundarnih telefonskih mreža značajno varira tijekom vremena. Tijekom radnog dana prometna krivulja ima dva ili čak tri vrha (Slika 9).

Slika 9. Oscilacije u prometu tijekom dana

Sat u danu u kojem promet, promatrano dulje vrijeme, ima najveću vrijednost naziva se najopterećeniji sat (HHH). Poznavanje prometa u CNN-u je od temeljne važnosti, jer određuje broj kanala (linija), količinu opreme postaja i čvorova. Promet istog dana u tjednu ima sezonske oscilacije. Ako je dan u tjednu predblagdan, tada je NPV tog dana veći od dana nakon praznika. Raste li broj usluga koje mreža podržava, raste i promet. Stoga je problematično s dovoljnom sigurnošću predvidjeti pojavu prometnih špica. Promet pomno nadziru mrežna administracija i projektantske organizacije. Pravila mjerenja prometa razvija ITU-T, a koriste ih nacionalne mrežne uprave kako bi zadovoljile zahtjeve kvalitete usluge kako za pretplatnike vlastite mreže tako i za pretplatnike drugih mreža povezanih s njom. Teorija teleprometa može se koristiti za praktične proračune gubitaka ili obujma opreme stanice (čvora) samo ako je promet stacionaran (statistički stabilan). Ovaj uvjet je približno zadovoljen prometom na CNN-u. Količina opterećenja primljenog dnevno na PBX utječe na prevenciju i popravak opreme. Neravnomjernost opterećenja postaje tijekom dana određena je koeficijentom koncentracije

Stroža definicija NNN je sljedeća. Preporuka ITU E.500 propisuje analizu podataka o intenzitetu za 12 mjeseci, odabir 30 najprometnijih dana od njih, pronalaženje najprometnijih sati u te dane i prosjek rezultata mjerenja intenziteta u tim intervalima. Ovaj izračun intenziteta prometa (opterećenja) naziva se normalnom procjenom intenziteta prometa u satu prometa ili razini A. Stroža procjena može se izračunati u prosjeku za 5 najprometnijih dana odabranog razdoblja od 30 dana. Takva se ocjena naziva povećana ili ocjena razine B.

Proces stvaranja prometa. Kao što svaki korisnik telefonske mreže zna, ne završavaju svi pokušaji uspostavljanja veze s pozvanim pretplatnikom uspješno. Ponekad morate napraviti nekoliko neuspješnih pokušaja prije nego što se uspostavi željena veza.

Slika 10. Dijagram događaja kada se uspostavi veza između pretplatnika

Razmotrimo moguće događaje prilikom simulacije uspostavljanja veze između pretplatnika A i B (slika 10). Statistički podaci o pozivima u telefonskim mrežama su sljedeći: udio obavljenih poziva je 70-50%, udio neuspjelih poziva je 30-50%. Svaki pokušaj pretplatnika zauzima ulaz u QS. Kod uspješnih pokušaja (kada je došlo do razgovora) vrijeme zauzetosti sklopnih uređaja koji uspostavljaju veze između ulaza i izlaza je duže nego kod neuspješnih pokušaja. Pretplatnik može prekinuti pokušaje povezivanja u bilo kojem trenutku. Ponovni pokušaji mogu biti uzrokovani sljedećim razlozima:

Neispravno biran broj;

Pretpostavka greške u mreži;

Stupanj hitnosti razgovora;

Neuspješni prethodni pokušaji;

Poznavanje navika pretplatnika B;

Sumnja u ispravno biranje.

Može se pokušati ponoviti ovisno o sljedećim okolnostima:

Stupnjevi hitnosti;

Procjene razloga neuspjeha;

Procjene svrsishodnosti ponavljanja pokušaja,

Procjene prihvatljivog intervala između pokušaja.

Odbijanje ponovnog pokušaja može biti povezano s niskim stupnjem hitnosti. Postoji nekoliko vrsta prometa koji generiraju pozivi: dolazni (ponuđeni) Y p i propušteni Y p. Promet Y p uključuje sve uspješne i neuspješne pokušaje, promet Y p koji je dio Y p uključuje uspješne i dio neuspješnih pokušaja:

Y pr \u003d Y p + Y np,

gdje je Y p - razgovorni (koristan) promet, a Y np - promet nastao neuspješnim pokušajima. Jednakost Y p = Y p moguća je samo u idealnom slučaju, ako nema gubitaka, pogrešaka pozivatelja i odaziva pozvanih pretplatnika.

Razlika između dolaznog i propuštenog opterećenja za određeno vremensko razdoblje bit će izgubljeno opterećenje.

Predviđanje prometa. Ograničeni resursi dovode do potrebe za postupnim širenjem postaje i mreže. Administracija mreže predviđa povećanje prometa tijekom faze razvoja, s obzirom na sljedeće:

Prihod je određen udjelom prijeđenog prometa Y p, - troškovi su određeni kvalitetom usluge pri najvećem prometu;

Veliki udio gubitaka (niska kvaliteta) javlja se u rijetkim slučajevima i tipičan je za kraj razvojnog razdoblja;

Najveći obujam propuštenog prometa pada na razdoblja kada praktički nema gubitaka - ako su gubici manji od 10%, pretplatnici na njih ne odgovaraju. Pri planiranju razvoja kolodvora i mreže projektant mora odgovoriti na pitanje koji su zahtjevi za kvalitetu pružanja usluge (za gubitke). Da biste to učinili, potrebno je izmjeriti gubitke u prometu prema pravilima usvojenim u zemlji.

Primjer mjerenja prometa.

Prvo razmislite kako možete prikazati rad QS-a koji ima nekoliko resursa koji opslužuju određeni promet u isto vrijeme. Dalje ćemo govoriti o takvim resursima kao što su poslužitelji koji služe protoku aplikacija ili zahtjeva. Jedan od najvizualnijih i najčešće korištenih načina za prikaz procesa servisiranja zahtjeva od strane skupa poslužitelja je gantogram. Ovaj grafikon je pravokutni koordinatni sustav, čija apscisa predstavlja vrijeme, a ordinata predstavlja diskretne točke koje odgovaraju serverima bazena. Slika 11 prikazuje gantogram za sustav s tri poslužitelja.

U prva tri vremenska intervala (smatramo ih sekundom) zauzeti su prvi i treći server, sljedeće dvije sekunde - samo treći, zatim drugi radi jednu sekundu, zatim drugi i prvi dvije sekunde, a zadnje dvije sekunde - samo prvi.

Konstruirani dijagram omogućuje izračunavanje količine prometa i njegovog intenziteta. Dijagram prikazuje samo opsluženi ili propušteni promet, budući da ne govori ništa o tome jesu li u sustav ušli zahtjevi koje poslužitelji nisu mogli poslužiti.

Količina prijeđenog prometa izračunava se kao ukupna duljina svih segmenata gantograma. Glasnoća za 10 sekundi:

Pridružite svakom vremenskom intervalu iscrtanom duž apscise, cijeli broj jednak broju poslužitelja zauzetih u ovom pojedinačnom intervalu. Ova vrijednost A(t) je trenutni intenzitet. Za naš primjer

A(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Nađimo sada prosječni intenzitet prometa u razdoblju od 10 sekundi

Dakle, prosječni intenzitet prometa koji prolazi razmatrani sustav od tri poslužitelja jednak je 1,5 Erl.

Glavni parametri opterećenja

Telefonsku komunikaciju koriste različite kategorije pretplatnika, koje karakteriziraju:

broj izvora opterećenja - N,

prosječan broj poziva iz jednog izvora u određenom vremenu (obično HNN) - s,

prosječno trajanje jedne okupacije komutacijskog sustava pri opsluživanju jednog poziva je t.

Intenzitet opterećenja bit će

Definirajmo različite izvore poziva. Na primjer,

Prosječan broj poziva po uredskom telefonu po uredskom telefonu;

Prosječan broj poziva s jednog apartmanskog pojedinačnog uređaja; slučajni događaj queuing teletraffic

s brojanjem - isto iz aparata za zajedničku uporabu;

sa ma - isto iz jedne kovanice;

sa sl - isto iz jedne spojne linije.

Tada je prosječan broj poziva iz jednog izvora:

Postoje približni podaci za prosječan broj poziva iz jednog izvora odgovarajuće kategorije:

3,5 - 5, \u003d 0,5 - 1, s brojanjem \u003d 1,5 - 2, s ma = 15 - 30, s sl \u003d 10 - 30.

Postoje sljedeće vrste veza koje, ovisno o ishodu veze, stvaraju različito telefonsko opterećenje stanice:

k p - koeficijent koji pokazuje udio veza koje su završile razgovorom;

k c - veze koje nisu završile razgovorom zbog zauzetosti pozvanog pretplatnika;

k but - koeficijent koji izražava udio veza koje nisu završile razgovorom zbog neodazivanja pozvanog pretplatnika;

k osh - veze koje nisu završile razgovorom zbog pogrešaka pozivatelja;

k od njih - pozivi koji nisu završili razgovorom iz tehničkih razloga.

Tijekom normalnog rada mreže, vrijednosti ovih koeficijenata su jednake:

k p = 0,60-0,75; kc = 0,12-0,15; k ali = 0,08-0,12; k osh =0,02-0,05; k one = 0,005-0,01.

Prosječno trajanje lekcije ovisi o vrsti veza. Na primjer, ako je veza završila razgovorom, prosječno trajanje zauzetosti uređaja t stanje bit će jednako

gdje je trajanje uspostave veze;

t kond. - razgovor koji je vođen;

t in - trajanje slanja poziva na telefonski aparat pozvanog pretplatnika;

t p - trajanje razgovora

gdje je t co - signal odziva stanice;

1.5n - vrijeme biranja pozivanog pretplatnika (n - broj znakova u broju);

t sa - vrijeme potrebno za uspostavljanje veze preklapanjem mehanizama i prekidanje veze nakon završetka razgovora. Približne vrijednosti razmatranih količina:

t co \u003d 3 sek., t c \u003d 1-2,5 sek., t in = 8-10 sek., t p = 90-130 sek.

Pozivi koji ne završavaju razgovorom također stvaraju opterećenje telefona.

Prosječno vrijeme zauzetosti uređaja kada je pozvani pretplatnik zauzet jednako je

gdje je postavljeno t. određeno prema (4.2.3)

t zujalica - vrijeme slušanja zujalice zauzeća, t zujalica =6sek.

Prosječno trajanje zauzetosti uređaja kada se pozvani pretplatnik ne javlja jednako je

gdje je t pv vrijeme slušanja kontrolnog signala povratnog zvona, t pv = 20 sek.

Ako nije bilo razgovora zbog grešaka pretplatnika, tada je prosječno t osh = 30 sek.

Trajanje seansi koje iz tehničkih razloga nisu završile razgovorom nije definirano jer je postotak takvih seansi mali.

Iz svega navedenog proizlazi da je ukupno opterećenje koje stvara skupina izvora za NTT jednako zbroju opterećenja pojedinih vrsta zanimanja.

gdje je koeficijent koji uzima u obzir pojmove kao dionice

Na telefonskoj mreži sa sedmeroznamenkastim numeriranjem projektirana je automatska telefonska centrala čiji je strukturni sastav pretplatnika sljedeći:

N chr = 4000, N ind = 1000, N broj = 2000, N ma = 400, N sl = 400.

Prosječan broj poziva koji dolaze iz jednog izvora u satu zauzetosti je

Formulama (4.2.3) i (4.2.6) nalazimo opterećenje

1.10.62826767 sek = 785.2 Hz.

Prosječno trajanje sata t iz formule Y=Nct

t= Y/Nc= 2826767/7800*3,8=95,4 sek.

Učitaj zadatak

1. Na telefonskoj mreži sa sedmeroznamenkastim numeriranjem projektirana je automatska telefonska centrala čiji je strukturni sastav pretplatnika sljedeći:

N uchr \u003d 5000, N ind \u003d 1500, N count = 3000, N ma \u003d 500, N sl \u003d 500.

Odredite teret koji stiže na stanicu - Y, prosječno trajanje zauzetosti t, ako je poznato da

s uhr \u003d 4, s ind \u003d 1, s brojanjem \u003d 2, s ma \u003d 10, sa sl \u003d 12, t p \u003d 120 s., t in \u003d 10 s., k p \u003d 0,6, t s \u003d 1 s., \u 003d 1.1.

Domaćin na Allbest.ru

Slični dokumenti

Koncept jednoliko raspodijeljene slučajne varijable. Multiplikativna kongruentna metoda. Modeliranje kontinuiranih slučajnih varijabli i diskretnih distribucija. Algoritam za simulaciju ekonomskih odnosa između zajmodavca i zajmoprimca.

seminarski rad, dodan 01.03.2011


Opći pojmovi teorije čekanja. Značajke modeliranja sustava čekanja. QS grafikoni stanja, jednadžbe koje ih opisuju. Opće karakteristike varijanti modela. Analiza sustava čekanja u supermarketima.

seminarski rad, dodan 17.11.2009


Elementi teorije čekanja. Matematičko modeliranje sustava čekanja, njihova klasifikacija. Simulacijsko modeliranje sustava čekanja. Praktična primjena teorije, rješavanje problema matematičkim metodama.

seminarski rad, dodan 04.05.2011


Pojam slučajnog procesa. Zadaci teorije čekanja. Klasifikacija sustava čekanja (QS). Probabilistički matematički model. Utjecaj slučajnih faktora na ponašanje objekta. Jednokanalni i višekanalni QS s čekanjem.

seminarski rad, dodan 25.09.2014


Proučavanje teorijskih aspekata učinkovite konstrukcije i rada sustava čekanja, njegovih glavnih elemenata, klasifikacije, karakteristika i performansi. Modeliranje sustava čekanja u GPSS jeziku.

seminarski rad, dodan 24.09.2010


Razvoj teorije dinamičkog programiranja, mrežnog planiranja i upravljanja proizvodnjom proizvoda. Sastavnice teorije igara u problemima modeliranja ekonomskih procesa. Elementi praktične primjene teorije čekanja čekanja.

praktični rad, dodano 01.08.2011


Elementarni pojmovi o slučajnim događajima, veličinama i funkcijama. Numeričke karakteristike slučajnih varijabli. Vrste asimetrije distribucija. Statistička procjena distribucije slučajnih varijabli. Rješavanje problema strukturno-parametarske identifikacije.

seminarski rad, dodan 06.03.2012


Modeliranje procesa čekanja. Različite vrste kanala čekanja. Rješenje jednokanalnog modela čekanja s kvarovima. Gustoća distribucije trajanja usluge. Definicija apsolutne propusnosti.

test, dodan 15.03.2016


Funkcionalne karakteristike sustava čekanja u cestovnom prometu, njegova struktura i glavni elementi. Kvantitativni pokazatelji kvalitete funkcioniranja sustava čekanja, postupak i glavne faze njihovog određivanja.

laboratorijski rad, dodano 11.03.2011


Postavljanje cilja modeliranja. Identifikacija stvarnih objekata. Odabir vrste modela, matematičke sheme. Konstrukcija kontinuirano-stohastičkog modela. Osnovni pojmovi teorije čekanja. Definirajte tijek događaja. Iskaz algoritama.