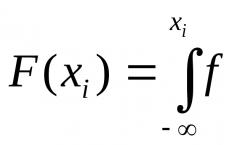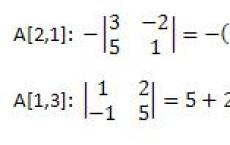Data je matrica inverza i algoritam za njezin izračun. Pronađite inverznu matricu online

Početna prema formuli: A^-1 = A*/detA, gdje je A* pridružena matrica, detA je izvorna matrica. Priložena matrica je transponirana matrica dodataka elementima izvorne matrice.

Prije svega, pronađite determinantu matrice, ona mora biti različita od nule, jer će se tada determinanta koristiti kao djelitelj. Neka je, na primjer, dana matrica treće (koja se sastoji od tri retka i tri stupca). Kao što vidite, determinanta matrice nije jednaka nuli, tako da postoji inverzna matrica.

Nađite komplement svakom elementu matrice A. Komplement A je determinanta podmatrice dobivena iz izvorne brisanjem i-tog retka i j-tog stupca, a ta determinanta se uzima s predznakom. Predznak se određuje množenjem determinante s (-1) na potenciju i+j. Tako će, na primjer, komplement A biti determinanta koja se razmatra na slici. Predznak je ispao ovako: (-1)^(2+1) = -1.

Kao rezultat ćete dobiti matrica dodaci, sada ga transponirajte. Transpozicija je operacija koja je simetrična u odnosu na glavnu dijagonalu matrice, stupci i retci se mijenjaju. Dakle, pronašli ste pridruženu matricu A*.

Ova tema jedna je od najomraženijih među studentima. Gore, vjerojatno, samo odrednice.

Trik je u tome što nas sam koncept inverznog elementa (ne govorim sada samo o matricama) upućuje na operaciju množenja. Čak iu školskom kurikulumu množenje se smatra složenom operacijom, a matrično množenje općenito je zasebna tema, kojoj sam posvetio cijeli odlomak i video lekciju.

Danas nećemo ulaziti u detalje matričnih izračuna. Samo zapamtite: kako se matrice označavaju, kako se množe i što iz toga slijedi.

Pregled: Množenje matrice

Prije svega, dogovorimo se oko notacije. Matrica $A$ veličine $\left[ m\times n \right]$ jednostavno je tablica brojeva s točno $m$ redaka i $n$ stupaca:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ ((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn )) \\\end(matrica) \desno])_(n)\]

Da ne biste slučajno mjestimično pobrkali redove i stupce (vjerujte mi, na ispitu možete pobrkati jedan s dvojkom - što reći o nekim tamo redovima), samo pogledajte sliku:

Određivanje indeksa za ćelije matrice

Što se događa? Ako postavimo standardni koordinatni sustav $OXY$ u gornji lijevi kut i usmjerimo osi tako da pokrivaju cijelu matricu, tada se svaka ćelija ove matrice može jedinstveno povezati s koordinatama $\lijevo(x;y \desno)$ - to će biti broj reda i broj stupca.

Zašto je koordinatni sustav postavljen točno u gornji lijevi kut? Da, jer odatle počinjemo čitati sve tekstove. Vrlo je lako zapamtiti.

Zašto je $x$ os usmjerena prema dolje, a ne udesno? Opet, jednostavno je: uzmite standardni koordinatni sustav ($x$-os ide udesno, $y$-os ide gore) i zarotirajte ga tako da obuhvati matricu. Ovo je rotacija od 90 stupnjeva u smjeru kazaljke na satu - njen rezultat vidimo na slici.

Općenito, shvatili smo kako odrediti indekse elemenata matrice. Sada se pozabavimo množenjem.

Definicija. Matrice $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$, kada broj stupaca u prvoj odgovara broju redaka u drugoj, nazivaju se konzistentnima.

Tim je redom. Može se biti dvosmisleno i reći da matrice $A$ i $B$ tvore uređeni par $\left(A;B \right)$: ako su konzistentne u ovom redoslijedu, onda uopće nije nužno da $B$ i $A$, tj. par $\left(B;A \right)$ također je konzistentan.

Samo konzistentne matrice mogu se množiti.

Definicija. Umnožak konzistentnih matrica $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$ nova je matrica $C=\left[ m\times k \right]$ čiji se elementi $((c)_(ij))$ izračunavaju po formuli:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Drugim riječima: da biste dobili element $((c)_(ij))$ matrice $C=A\cdot B$, morate uzeti $i$-redak prve matrice, $j$-ti stupac druge matrice, a zatim pomnožiti elemente iz tog retka i stupca u parovima. Zbrojite rezultate.

Da, to je surova definicija. Iz toga odmah proizlazi nekoliko činjenica:

1. Množenje matrica je, općenito govoreći, nekomutativno: $A\cdot B\ne B\cdot A$;
2. Međutim, množenje je asocijativno: $\lijevo(A\cdot B \desno)\cdot C=A\cdot \lijevo(B\cdot C \desno)$;
3. Pa čak i distributivno: $\lijevo(A+B \desno)\cdot C=A\cdot C+B\cdot C$;
4. I opet distribucija: $A\cdot \lijevo(B+C \desno)=A\cdot B+A\cdot C$.

Distributivnost množenja je morala biti opisana odvojeno za lijevi i desni množitelj-zbroj samo zbog nekomutativnosti operacije množenja.

Ako se ipak pokaže da je $A\cdot B=B\cdot A$, takve se matrice nazivaju permutabilnim.

Među svim matricama koje se tamo nečim množe, postoje posebne - one koje, kada se pomnože s bilo kojom matricom $A$, opet daju $A$:

Definicija. Matrica $E$ naziva se identitetom ako je $A\cdot E=A$ ili $E\cdot A=A$. U slučaju kvadratne matrice $A$ možemo napisati:

Matrica identiteta je čest gost u rješavanju matričnih jednadžbi. I općenito, čest gost u svijetu matrica. :)

I zbog ovog $E$ netko je smislio svu igru ​​koja će biti napisana sljedeće.

Što je inverzna matrica

Budući da je množenje matrice vrlo dugotrajna operacija (morate pomnožiti hrpu redaka i stupaca), koncept inverzne matrice također nije najtrivijalniji. I treba neko objašnjenje.

Ključna definicija

Pa, vrijeme je da saznamo istinu.

Definicija. Matrica $B$ se naziva inverzom matrice $A$ ako

Inverzna matrica je označena sa $((A)^(-1))$ (ne brkati sa stupnjem!), tako da se definicija može prepisati ovako:

Čini se da je sve vrlo jednostavno i jasno. Ali kada se analizira takva definicija, odmah se postavlja nekoliko pitanja:

1. Postoji li uvijek inverzna matrica? A ako ne uvijek, kako onda odrediti: kada postoji, a kada ne?
2. I tko je rekao da je takva matrica točno jedna? Što ako za neku izvornu matricu $A$ postoji cijela gomila inverza?
3. Kako izgledaju svi ti "obrati"? A kako ih zapravo prebrojati?

Što se tiče algoritama izračuna - o tome ćemo govoriti malo kasnije. Ali na ostala pitanja ćemo odgovoriti odmah. Posložimo ih u obliku zasebnih tvrdnji-lema.

Osnovna svojstva

Počnimo s tim kako bi matrica $A$ trebala izgledati da bi imala $((A)^(-1))$. Sada ćemo provjeriti moraju li obje ove matrice biti kvadratne i iste veličine: $\left[ n\times n \right]$.

Lema 1. Dana je matrica $A$ i njezin inverz $((A)^(-1))$. Tada su obje ove matrice kvadratne i imaju isti red $n$.

Dokaz. Sve je jednostavno. Neka je matrica $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Budući da proizvod $A\cdot ((A)^(-1))=E$ postoji po definiciji, matrice $A$ i $((A)^(-1))$ su konzistentne tim redoslijedom:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end(align)\]

Ovo je izravna posljedica algoritma množenja matrice: koeficijenti $n$ i $a$ su "tranzitni" i moraju biti jednaki.

Ujedno je definirano i inverzno množenje: $((A)^(-1))\cdot A=E$, pa su matrice $((A)^(-1))$ i $A$ konzistentne i ovim redoslijedom:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end(align)\]

Stoga, bez gubitka općenitosti, možemo pretpostaviti da je $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Međutim, prema definiciji $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, tako da su dimenzije matrica potpuno iste:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Dakle, ispada da su sve tri matrice - $A$, $((A)^(-1))$ i $E$ - kvadratne veličine $\left[ n\times n \right]$. Lema je dokazana.

Pa to je već dobro. Vidimo da su samo kvadratne matrice invertibilne. Sada se uvjerimo da je inverzna matrica uvijek ista.

Lema 2. Dana je matrica $A$ i njezin inverz $((A)^(-1))$. Tada je ova inverzna matrica jedinstvena.

Dokaz. Pođimo od suprotnog: neka matrica $A$ ima barem dvije instance inverza — $B$ i $C$. Tada su prema definiciji istinite jednakosti:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(align)\]

Iz leme 1 zaključujemo da su sve četiri matrice $A$, $B$, $C$ i $E$ kvadratne istog reda: $\left[ n\times n \right]$. Stoga je proizvod definiran:

Budući da je množenje matrica asocijativno (ali ne i komutativno!), možemo napisati:

\[\begin(align) & B\cdot A\cdot C=\lijevo(B\cdot A \desno)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \lijevo(A\cdot C \desno)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end(align)\]

Dobili smo jedinu moguću opciju: dvije kopije inverzne matrice su jednake. Lema je dokazana.

Gornje obrazloženje gotovo doslovce ponavlja dokaz jedinstvenosti inverznog elementa za sve realne brojeve $b\ne 0$. Jedini značajan dodatak je uzimanje u obzir dimenzija matrica.

Međutim, još uvijek ne znamo ništa o tome je li bilo koja kvadratna matrica invertibilna. Ovdje nam u pomoć dolazi determinanta - to je ključna karakteristika za sve kvadratne matrice.

Lema 3. Zadana je matrica $A$. Ako matrica $((A)^(-1))$ inverzna njoj postoji, tada je determinanta izvorne matrice različita od nule:

\[\lijevo| A \desno|\ne 0\]

Dokaz. Već znamo da su $A$ i $((A)^(-1))$ kvadratne matrice veličine $\left[ n\times n \right]$. Stoga je za svaku od njih moguće izračunati determinantu: $\left| A \desno|$ i $\lijevo| ((A)^(-1)) \desno|$. Međutim, determinanta umnoška jednaka je umnošku determinanti:

\[\lijevo| A\cdot B \desno|=\lijevo| A \desno|\cdot \lijevo| B \desno|\desna strelica \lijevo| A\cdot ((A)^(-1)) \desno|=\lijevo| A \desno|\cdot \lijevo| ((A)^(-1)) \desno|\]

Ali prema definiciji $A\cdot ((A)^(-1))=E$, a determinanta $E$ je uvijek jednaka 1, tako da

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \lijevo| A\cdot ((A)^(-1)) \desno|=\lijevo| E\desno|; \\ & \lijevo| A \desno|\cdot \lijevo| ((A)^(-1)) \desno|=1. \\ \end(align)\]

Umnožak dvaju brojeva jednak je jedinici samo ako je svaki od tih brojeva različit od nule:

\[\lijevo| A \right|\ne 0;\quad \lijevo| ((A)^(-1)) \right|\ne 0.\]

Dakle, ispada da je $\left| A \desno|\ne 0$. Lema je dokazana.

Zapravo, ovaj zahtjev je sasvim logičan. Sada ćemo analizirati algoritam za pronalaženje inverzne matrice - i postat će potpuno jasno zašto u načelu ne može postojati inverzna matrica s nultom determinantom.

Ali prvo, formulirajmo "pomoćnu" definiciju:

Definicija. Degenerirana matrica je kvadratna matrica veličine $\left[ n\times n \right]$ čija je determinanta nula.

Dakle, možemo tvrditi da je svaka invertibilna matrica nedegenerirana.

Kako pronaći inverznu matricu

Sada ćemo razmotriti univerzalni algoritam za pronalaženje inverznih matrica. Općenito, postoje dva općeprihvaćena algoritma, a danas ćemo razmotriti i drugi.

Ona koju ćemo sada razmotriti vrlo je učinkovita za matrice veličine $\left[ 2\times 2 \right]$ i - dijelom - veličine $\left[ 3\times 3 \right]$. Ali počevši od veličine $\left[ 4\times 4 \right]$ bolje je ne koristiti ga. Zašto - sada ćete sve razumjeti.

Algebarski dodaci

Pripremi se. Sada će biti boli. Ne, ne brinite: lijepa medicinska sestra u suknji, čarapama s čipkom ne dolazi k vama i neće vam dati injekciju u stražnjicu. Sve je puno prozaičnije: algebarski dodaci i njezino veličanstvo "Union Matrix" dolaze vam.

Počnimo s onim glavnim. Neka postoji kvadratna matrica veličine $A=\left[ n\times n \right]$ čiji se elementi nazivaju $((a)_(ij))$. Tada se za svaki takav element može definirati algebarski komplement:

Definicija. Algebarski komplement $((A)_(ij))$ elementu $((a)_(ij))$ u $i$tom retku i $j$tom stupcu matrice $A=\left[ n\times n \right]$ je konstrukcija oblika

\[((A)_(ij))=((\lijevo(-1 \desno))^(i+j))\cdot M_(ij)^(*)\]

Gdje je $M_(ij)^(*)$ determinanta matrice dobivena iz originalnog $A$ brisanjem istog $i$-tog retka i $j$-tog stupca.

Opet. Algebarski komplement elementu matrice s koordinatama $\left(i;j \right)$ označava se kao $((A)_(ij))$ i izračunava se prema shemi:

1. Prvo brišemo $i$-redak i $j$-ti stupac iz originalne matrice. Dobivamo novu kvadratnu matricu, a njenu determinantu označavamo kao $M_(ij)^(*)$.
2. Zatim pomnožimo ovu determinantu s $((\left(-1 \right))^(i+j))$ - isprva se ovaj izraz može činiti nevjerojatnim, ali zapravo samo otkrivamo znak ispred $M_(ij)^(*)$.
3. Brojimo - dobivamo određeni broj. Oni. algebarsko zbrajanje je samo broj, a ne neka nova matrica, i tako dalje.

Sama matrica $M_(ij)^(*)$ naziva se komplementarni minor elementu $((a)_(ij))$. I u tom smislu, gornja definicija algebarskog komplementa poseban je slučaj složenije definicije - one koju smo razmatrali u lekciji o determinanti.

Važna nota. Zapravo, u "odrasloj" matematici, algebarski dodaci se definiraju na sljedeći način:

1. Uzimamo $k$ redaka i $k$ stupaca u kvadratnoj matrici. Na njihovom sjecištu dobivamo matricu veličine $\left[ k\times k \right]$ — njezina se determinanta naziva minor reda $k$ i označava se s $((M)_(k))$.
2. Zatim prekrižimo tih "odabranih" $k$ redaka i $k$ stupaca. Ponovno dobivamo kvadratnu matricu - njezina se determinanta naziva komplementarni minor i označava se s $M_(k)^(*)$.
3. Pomnožite $M_(k)^(*)$ s $((\left(-1 \right))^(t))$, gdje je $t$ (sad pažnja!) zbroj brojeva svih odabranih redaka i stupaca. Ovo će biti algebarsko zbrajanje.

Pogledajte treći korak: zapravo postoji zbroj od $2k$ pojmova! Druga stvar je da za $k=1$ dobivamo samo 2 člana - to će biti isti $i+j$ - "koordinate" elementa $((a)_(ij))$, za koji tražimo algebarski komplement.

Stoga danas koristimo malo pojednostavljenu definiciju. No, kako ćemo kasnije vidjeti, bit će i više nego dovoljno. Puno važnije je sljedeće:

Definicija. Matrica unije $S$ u kvadratnu matricu $A=\left[ n\times n \right]$ nova je matrica veličine $\left[ n\times n \right]$, koja se dobiva iz $A$ zamjenom $((a)_(ij))$ s algebarskim dodacima $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ ((A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn) )) \\\end(matrica) \desno]\]

Prva misao koja se javlja u trenutku spoznaje ove definicije je "evo koliko morate ukupno izbrojati!" Opustite se: morate računati, ali ne toliko. :)

Pa, sve je to jako lijepo, ali zašto je potrebno? Ali zašto.

Glavni teorem

Vratimo se malo unatrag. Zapamtite, lema 3 tvrdi da je invertibilna matrica $A$ uvijek nesingularna (to jest, njena determinanta nije nula: $\left| A \right|\ne 0$).

Dakle, vrijedi i obrnuto: ako matrica $A$ nije degenerirana, onda je uvijek invertibilna. A postoji čak i shema pretraživanja $((A)^(-1))$. Provjerite:

Teorem o inverznoj matrici. Neka je dana kvadratna matrica $A=\left[ n\times n \right]$, a njena determinanta nije nula: $\left| A \desno|\ne 0$. Tada inverzna matrica $((A)^(-1))$ postoji i izračunava se po formuli:

\[((A)^(-1))=\frac(1)(\lijevo| A \desno|)\cdot ((S)^(T))\]

A sada - sve isto, ali čitkim rukopisom. Da biste pronašli inverznu matricu, trebate:

1. Izračunajte determinantu $\left| \right|$ i uvjerite se da nije nula.
2. Sastavite matricu unije $S$, tj. izbroji 100500 algebarskih sabiraka $((A)_(ij))$ i stavi ih na mjesto $((a)_(ij))$.
3. Transponirajte ovu matricu $S$ i zatim je pomnožite s nekim brojem $q=(1)/(\left| A \right|)\;$.

I to je to! Nađena je inverzna matrica $((A)^(-1))$. Pogledajmo primjere:

\[\lijevo[ \početak(matrica) 3 & 1 \\ 5 & 2 \\\kraj(matrica) \desno]\]

Riješenje. Provjerimo reverzibilnost. Izračunajmo determinantu:

\[\lijevo| A \desno|=\lijevo| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Determinanta je različita od nule. Dakle, matrica je invertibilna. Kreirajmo matricu unije:

Izračunajmo algebarske dodatke:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\desno|=2; \\ & ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| 5\desno|=-5; \\ & ((A)_(21))=((\lijevo(-1 \desno))^(2+1))\cdot \lijevo| 1 \desno|=-1; \\ & ((A)_(22))=((\lijevo(-1 \desno))^(2+2))\cdot \lijevo| 3\desno|=3. \\ \end(align)\]

Obratite pažnju na odrednice |2|, |5|, |1| i |3| su determinante matrica veličine $\left[ 1\times 1 \right]$, a ne moduli. Oni. ako su u determinantama bili negativni brojevi, nije potrebno uklanjati "minus".

Ukupno, naša sindikalna matrica izgleda ovako:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ((\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin(array)(* (35) (r)) 2 & -1 \\ -5 & 3 \\\end(niz) \desno]\]

OK, sada je sve gotovo. Problem riješen.

Odgovor. $\lijevo[ \begin(niz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(niz) \desno]$

Zadatak. Nađi inverznu matricu:

\[\lijevo[ \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \desno]\]

Riješenje. Opet, razmatramo determinantu:

\[\begin(align) & \left| \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \right|=\begin(matrica) \lijevo(1\cdot 2\cdot 1+\lijevo(-1 \desno)\cdot \lijevo(-1 \desno)\cdot 1+2\cdot 0\cdo t 0 \desno)- \\ -\lijevo(2\cdot 2\cdot 1+\lijevo(-1 \desno)\cdot 0\cdot 1+1\cdot \lijevo(-1 \desno)\cdot 0 \desno) \\\end(matrica)= \\ & =\lijevo(2+1+0 \desno)-\lijevo(4+0+0 \desno)=-1\ne 0. \\ \ end(align )\]

Determinanta je različita od nule - matrica je invertibilna. Ali sada će biti najsitnije: morate izbrojati čak 9 (devet, kvragu!) algebarskih sabrajavanja. I svaki od njih će sadržavati kvalifikator $\left[ 2\times 2 \right]$. Letio:

\[\begin(matrica) ((A)_(11))=((\lijevo(-1 \desno))^(1+1))\cdot \lijevo| \početak(matrica) 2 & -1 \\ 0 & 1 \\\kraj(matrica) \desno|=2; \\ ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| \begin(matrica) 0 & -1 \\ 1 & 1 \\\end(matrica) \right|=-1; \\ ((A)_(13))=((\lijevo(-1 \desno))^(1+3))\cdot \lijevo| \početak(matrica) 0 & 2 \\ 1 & 0 \\\kraj(matrica) \desno|=-2; \\ ... \\ ((A)_(33))=((\lijevo(-1 \desno))^(3+3))\cdot \lijevo| \početak(matrica) 1 & -1 \\ 0 & 2 \\\kraj(matrica) \desno|=2; \\ \kraj(matrica)\]

Ukratko, matrica unije će izgledati ovako:

Stoga će inverzna matrica biti:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 &-2 \\\end(niz) \desno]\]

Pa, to je sve. Evo odgovora.

Odgovor. $\lijevo[ \begin(niz)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(niz) \desno]$

Kao što vidite, na kraju svakog primjera izvršili smo provjeru. S tim u vezi, važna napomena:

Nemojte biti lijeni provjeriti. Pomnožite izvornu matricu s pronađenim inverzom - trebali biste dobiti $E$.

Mnogo je lakše i brže izvršiti ovu provjeru nego tražiti pogrešku u daljnjim izračunima, kada npr. rješavate matričnu jednadžbu.

Alternativni način

Kao što sam rekao, teorem o inverznoj matrici odlično funkcionira za veličine $\left[ 2\times 2 \right]$ i $\left[ 3\times 3 \right]$ (u potonjem slučaju više nije tako "savršeno"), ali za veće matrice to je potpuno tužno.

Ali ne brinite: postoji alternativni algoritam koji se može koristiti za mirno pronalaženje inverza čak i za matricu $\left[ 10\times 10 \right]$. Ali, kao što je često slučaj, da bismo razmotrili ovaj algoritam, trebamo malo teorijske pozadine.

Elementarne transformacije

Među različitim transformacijama matrice postoji nekoliko posebnih - nazivaju se elementarnim. Postoje točno tri takve transformacije:

1. Množenje. Možete uzeti $i$-ti redak (stupac) i pomnožiti ga s bilo kojim brojem $k\ne 0$;
2. Dodatak. Dodajte $i$-tom retku (stupcu) bilo koji drugi $j$-ti red (stupac) pomnožen s bilo kojim brojem $k\ne 0$ (naravno, moguće je i $k=0$, ali koja je svrha? Ništa se neće promijeniti).
3. Permutacija. Uzmite $i$-ti i $j$-ti red (kolone) i zamijenite ih.

Zašto se te transformacije nazivaju elementarnim (za velike matrice ne izgledaju tako elementarno) i zašto ih ima samo tri - ova su pitanja izvan opsega današnje lekcije. Stoga nećemo ulaziti u detalje.

Još jedna stvar je važna: sve te perverzije moramo izvesti na pridruženoj matrici. Da, da, dobro ste čuli. Sada će biti još jedna definicija - posljednja u današnjoj lekciji.

Priložena matrica

Sigurno ste u školi rješavali sustave jednadžbi metodom zbrajanja. Pa, eto, od jednog retka oduzmite drugi, pomnožite neki redak s brojem - to je sve.

Dakle: sada će sve biti isto, ali već "na odrasli način". Spreman?

Definicija. Neka su zadane matrica $A=\lijevo[ n\puta n \desno]$ i matrica identiteta $E$ iste veličine $n$. Zatim pridružena matrica $\left[ A\left| E \ desno. \right]$ je nova $\left[ n\times 2n \right]$ matrica koja izgleda ovako:

\[\lijevo[ A\lijevo| E \ desno. \right]=\lijevo[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Ukratko, uzmemo matricu $A$, s desne strane joj dodijelimo matricu identiteta $E$ potrebne veličine, odvajamo ih okomitom trakom radi ljepote - evo priložene. :)

U čemu je kvaka? I evo što:

Teorema. Neka je matrica $A$ invertibilna. Razmotrimo adjungiranu matricu $\left[ A\left| E \ desno. \desno]$. Ako koristite elementarne transformacije nizova dovesti ga u oblik $\left[ E\left| Svijetao. \right]$, tj. množenjem, oduzimanjem i preuređivanjem redaka da se iz $A$ dobije matrica $E$ s desne strane, tada je matrica $B$ dobivena s lijeve strane inverzna od $A$:

\[\lijevo[ A\lijevo| E \ desno. \desno]\na \lijevo[ E\lijevo| Svijetao. \desno]\desna strelica B=((A)^(-1))\]

Tako je jednostavno! Ukratko, algoritam za pronalaženje inverzne matrice izgleda ovako:

1. Napišite pridruženu matricu $\left[ A\left| E \ desno. \desno]$;
2. Izvršite elementarne konverzije nizova dok se desno umjesto $A$ ne pojavi $E$;
3. Naravno, nešto će se pojaviti i s lijeve strane - određena matrica $B$. Ovo će biti obrnuto;
4. DOBITAK! :)

Naravno, puno lakše reći nego učiniti. Dakle, pogledajmo nekoliko primjera: za veličine $\left[ 3\times 3 \right]$ i $\left[ 4\times 4 \right]$.

Zadatak. Nađi inverznu matricu:

\[\lijevo[ \početak(niz)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\kraj (niz) \desno]\]

Riješenje. Sastavljamo priloženu matricu:

\[\lijevo[ \početak(niz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\kraj (niz) \desno]\]

Budući da je posljednji stupac izvorne matrice ispunjen jedinicama, oduzmite prvi red od ostatka:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\\end(matri x)\to \ \ & \to \lijevo[ \begin(niz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\kraj (niz) \desno] \\ \end(align)\]

Nema više jedinica, osim prve linije. Ali ne diramo ga, inače će se novouklonjene jedinice početi "množiti" u trećem stupcu.

Ali možemo dvaput oduzeti drugu liniju od zadnje - dobit ćemo jedinicu u donjem lijevom kutu:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right]\begin(matrix) \ \\ \downarrow \\ -2 \\\end(matrix )\do \\ & \lijevo[ \begin(niz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj (niz) \desno] \\ \end(align)\]

Sada možemo oduzeti posljednji redak od prvog i dvaput od drugog - na taj način ćemo "izništiti" prvi stupac:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) -1 \\ -2 \\ \uparrow \\\end(matrix x)\to \ \ & \na \lijevo[ \begin(niz)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj (niz) \desno] \\ \end(align)\]

Pomnožite drugi red s −1 i zatim ga oduzmite 6 puta od prvog i dodajte 1 put posljednjem:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) \ \\ \left| \cdot \lijevo(-1 \desno) \desno. \\ \ \\\end(matrica)\to \\ & \na \lijevo[ \begin(niz)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno]\begin(matrica) -6 \\ \updownarrow \ \ +1 \ \\end(matrica)\to \\ & \to \lijevo[ \begin(niz)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\kraj (niz) \desno] \\ \end(align)\]

Ostaje samo zamijeniti redove 1 i 3:

\[\lijevo[ \početak(niz)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & -18 & 32 & -13 \\\kraj (niz) \desno]\]

Spreman! Desno je tražena inverzna matrica.

Odgovor. $\lijevo[ \begin(niz)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(niz) \desno]$

Zadatak. Nađi inverznu matricu:

\[\lijevo[ \početak(matrica) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\kraj (matrica) \desno]\]

Riješenje. Opet sastavljamo priloženi:

\[\lijevo[ \begin(niz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ kraj(niz)\desno]\]

Posudimo malo, brinemo se o tome koliko sada imamo za brojanje ... i počnemo brojati. Za početak, "nuliramo" prvi stupac oduzimanjem reda 1 od redaka 2 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(niz) \desno]\begin(matrica) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrica)\to \\ & \na \lijevo[ \begin(niz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & - 5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Vidimo previše "minusa" u recima 2-4. Pomnožite sva tri retka s −1, a zatim spalite treći stupac oduzimanjem retka 3 od ostatka:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(niz) \desno]\početak(matrica) \ \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\end(niz) \desno]\begin(matrica) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matrica)\to \\ & \na \lijevo[ \begin(niz)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Sada je vrijeme da "spržite" posljednji stupac originalne matrice: oduzmite red 4 od ostatka:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno]\početak(matrica) +1 \\ -3 \\ -2 \\ \gore \\\kraj(matrica)\to \\ & \lijevo[ \početak(niz)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Završni niz: "spalite" drugi stupac oduzimanjem reda 2 od reda 1 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno]\begin(matrica) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matrica)\to \\ & \lijevo[ \begin(niz)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

I opet matrica identiteta lijevo, pa inverzno desno. :)

Odgovor. $\lijevo[ \begin(matrica) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & -1 \\\end(matrica) \right]$

OK, sada je sve gotovo. Provjerite sami - otpisan sam. :)

ALGEBARSKI PRIBRAJCI I MINORI

Uzmimo determinantu trećeg reda: .

Minor koji odgovara ovom elementu aij determinanta trećeg reda je determinanta drugog reda koja se dobiva iz zadane brisanjem retka i stupca u čijem se sjecištu zadani element nalazi, tj. ja-th line i j-ti stupac. Minori koji odgovaraju danom elementu aij označit ćemo M ij.

Na primjer, manji M12 koji odgovara elementu a 12, bit će odrednica 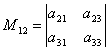, koja se dobiva brisanjem 1. retka i 2. stupca iz zadane determinante.

Dakle, formula koja određuje determinantu trećeg reda pokazuje da je ta determinanta jednaka zbroju umnožaka elemenata 1. reda i njihovih odgovarajućih minora; dok minor koji odgovara elementu a 12, uzima se sa znakom “–”, tj. može se to napisati

.

(1)

Slično se mogu uvesti definicije minora za determinante drugog reda i viših redova.

Predstavimo još jedan koncept.

Algebarsko zbrajanje element aij determinanta se naziva njen minor M ij pomnoženo s (–1) i+j .

Algebarsko zbrajanje elemenata aij označeno A ij.

Iz definicije dobivamo da je veza između algebarskog komplementa elementa i njegovog minora izražena jednakošću A ij= (–1) i+j M ij .

Na primjer,

Primjer. S obzirom na odrednicu. Pronaći A 13, A 21, A 32.

Lako je vidjeti da se pomoću algebarskih zbrajanja elemenata formula (1) može napisati kao:

Slično ovoj formuli, može se dobiti dekompozicija determinante na elemente bilo kojeg retka ili stupca.

Na primjer, dekompozicija determinante na elemente 2. reda može se dobiti na sljedeći način. Prema svojstvu 2 determinante imamo:

Dobivenu determinantu proširimo elementima 1. reda.

.

(2)

Odavde jer determinante drugog reda u formuli (2) su minori elemenata a 21, a 22, a 23. Dakle, tj. dobili smo proširenje determinante elementima 2. reda.

Slično se može dobiti dekompozicija determinante na elemente trećeg reda. Koristeći svojstvo 1 determinanti (na transpoziciju), može se pokazati da slična proširenja vrijede i za proširenja u elementima stupaca.

Dakle, sljedeća teorema je istinita.

Teorem (o proširenju determinante u danom retku ili stupcu). Determinanta je jednaka zbroju umnožaka elemenata bilo kojeg od njegovih redaka (ili stupaca) i njihovih algebarskih komplemenata.

Sve gore navedeno vrijedi za determinante bilo kojeg višeg reda.

Primjeri.

INVERZNA MATRICA

Koncept inverzne matrice uvodi se samo za kvadratne matrice.

Ako A onda je kvadratna matrica obrnuti za njega je matrica označena matrica A-1 i zadovoljavajući uvjet . (Ova definicija je uvedena po analogiji s množenjem brojeva)

Matrica $A^(-1)$ naziva se inverzom kvadratne matrice $A$ ako je zadovoljen uvjet $A^(-1)\cdot A=A\cdot A^(-1)=E$, gdje je $E$ matrica identiteta, čiji je red jednak redu matrice $A$.

Nesingularna matrica je matrica čija determinanta nije jednaka nuli. Prema tome, degenerirana matrica je ona čija je determinanta jednaka nuli.

Inverzna matrica $A^(-1)$ postoji ako i samo ako je matrica $A$ nesingularna. Ako inverzna matrica $A^(-1)$ postoji, onda je ona jedinstvena.

Postoji nekoliko načina da se pronađe inverz matrice, a mi ćemo pogledati dva od njih. Na ovoj stranici raspravljat će se o metodi adjungirane matrice, koja se smatra standardnom u većini tečajeva više matematike. Drugi način pronalaska inverzne matrice (metoda elementarnih transformacija), koji uključuje korištenje Gaussove metode ili Gauss-Jordanove metode, razmatra se u drugom dijelu.

Metoda adjungirane (unijske) matrice

Neka je dana matrica $A_(n\puta n)$. Da bi se pronašla inverzna matrica $A^(-1)$, potrebna su tri koraka:

1. Nađite determinantu matrice $A$ i uvjerite se da je $\Delta A\neq 0$, tj. da je matrica A nedegenerirana.
2. Sastavite algebarske komplemente $A_(ij)$ svakog elementa matrice $A$ i zapišite matricu $A_(n\times n)^(*)=\left(A_(ij) \right)$ od pronađenih algebarskih komplemenata.
3. Napišite inverznu matricu uzimajući u obzir formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Matrica $(A^(*))^T$ često se naziva adjungirana (uzajamna, udružena) matrica $A$.

Ako se odluka donosi ručno, tada je prva metoda dobra samo za matrice relativno malih redova: druga (), treća (), četvrta (). Za pronalaženje inverzne matrice za matricu višeg reda koriste se druge metode. Na primjer, Gaussova metoda o kojoj se govori u drugom dijelu.

Primjer #1

Pronađite matricu inverznu matrici $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & -1 & -9 & 0 \end(array) \right)$.

Kako su svi elementi četvrtog stupca jednaki nuli, onda je $\Delta A=0$ (tj. matrica $A$ je degenerirana). Budući da je $\Delta A=0$, ne postoji matrica inverzna $A$.

Odgovor: matrica $A^(-1)$ ne postoji.

Primjer #2

Pronađite matricu inverznu matrici $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Izvršite provjeru.

Koristimo metodu adjungirane matrice. Najprije pronađimo determinantu zadane matrice $A$:

$$ \Delta A=\lijevo| \begin(niz) (cc) -5 & 7\\ 9 & 8 \end(niz)\right|=-5\cdot 8-7\cdot 9=-103. $$

Budući da je $\Delta A \neq 0$, tada inverzna matrica postoji, pa nastavljamo s rješenjem. Pronalaženje algebarskih komplemenata

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(poravnano)

Sastavite matricu algebarskih komplemenata: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transponirajte dobivenu matricu: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (rezultirajuća matrica se često naziva pridružena ili unijska matrica matrici $A$). Koristeći formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, imamo:

$$ A^(-1)=\frac(1)(-103)\cdot \lijevo(\begin(niz) (cc) 8 & -7\\ -9 & -5 \end(niz)\desno) =\lijevo(\begin(niz) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \kraj (niz)\desno) $$

Dakle, inverzna matrica je pronađena: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$. Za provjeru istinitosti rezultata dovoljno je provjeriti istinitost jedne od jednakosti: $A^(-1)\cdot A=E$ ili $A\cdot A^(-1)=E$. Provjerimo jednakost $A^(-1)\cdot A=E$. Kako bismo manje radili s razlomcima, zamijenit ćemo matricu $A^(-1)$ ne u obliku $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$, već u obliku $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7 \\ -9 & -5 \end(array)\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdo t\left(\begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array)\right) =E $$

Odgovor: $A^(-1)=\lijevo(\početak(niz) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \kraj(niz)\desno)$.

Primjer #3

Pronađite inverz matrice $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$. Izvršite provjeru.

Počnimo s izračunavanjem determinante matrice $A$. Dakle, determinanta matrice $A$ je:

$$ \Delta A=\lijevo| \begin(niz) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(niz) \right| = 18-36+56-12=26. $$

Budući da je $\Delta A\neq 0$, onda inverzna matrica postoji, pa nastavljamo s rješenjem. Pronalazimo algebarske komplemente svakog elementa zadane matrice:

$$ \begin(aligned) & A_(11)=(-1)^(2)\cdot\left|\begin(array)(cc) 9 & 4\\ 3 & 2\end(array)\right|=6;\; A_(12)=(-1)^(3)\cdot\lijevo|\početak(niz)(cc) -4 &4 \\ 0 & 2\kraj(niz)\desno|=8;\; A_ (13) = (-1)^(4) \ cdot \ lijevo | \ početak (niz) (CC) -4 & 9 \\ 0 & 3 \ Kraj (niz) \ Desno | = -12; \\ & A_ (21) \ CDOT \ LIJEVO | \ BEGIN (Niz) (CC) 7 & 3 \\ 3 & 2 \ END (Niz) \ Desno | = -5; \; A_(22)=(-1)^(4)\cdot\lijevo|\početak(niza)(cc) 1 & 3\\ 0 & 2\kraj(niza)\desno|=2;\; A_(23)=(-1)^(5)\cdot\left|\begin(array)(cc) 1 & 7\\ 0 & 3\end(array)\right|=-3;\\ & A_(31)=(-1)^(4)\cdot\left|\begin(array)(cc) 7 & 3\\ 9 & 4\end(array)\right|=1;\; A_(32)=(-1)^(5)\cdot\lijevo|\begin(niz)(cc) 1 & 3\\ -4 & 4\end(niz)\desno|=-16;\; A_(33)=(-1)^(6)\cdot\lijevo|\begin(niz)(cc) 1 & 7\\ -4 & 9\end(niz)\desno|=37. \kraj(poravnano) $$

Sastavljamo matricu algebarskih sabiranja i transponiramo je:

$$ A^*=\lijevo(\početak(niza) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\kraj(niza) \desno); \; (A^*)^T=\lijevo(\početak(niza) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\kraj(niza) \desno). $$

Koristeći formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, dobivamo:

$$ A^(-1)=\frac(1)(26)\cdot \lijevo(\begin(niz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(niz) \desno)= \lijevo(\begin(niz) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/ 13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(niz) \desno) $$

Dakle $A^(-1)=\lijevo(\begin(niz) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(niz) \desno)$. Za provjeru istinitosti rezultata dovoljno je provjeriti istinitost jedne od jednakosti: $A^(-1)\cdot A=E$ ili $A\cdot A^(-1)=E$. Provjerimo jednakost $A\cdot A^(-1)=E$. Kako bismo manje radili s razlomcima, zamijenit ćemo matricu $A^(-1)$ ne u obliku $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, već u obliku $\fra c(1) (26)\cdot \lijevo(\begin(niz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(niz) \desno)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ - 12 & -3 & 37\end(niz) \desno) =\frac(1)(26)\cdot\lijevo(\početak(niz) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\kraj(niz) \desno) =\lijevo(\početak(niz) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \ \ 0 & 0 & 1\end(niz) \desno) =E $$

Provjera je uspješno prošla, inverzna matrica $A^(-1)$ je ispravno pronađena.

Odgovor: $A^(-1)=\lijevo(\početak(niz) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \kraj (niz) \desno)$.

Primjer #4

Pronađite inverznu matricu od $A=\lijevo(\begin(niz) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(niz) \desno)$.

Za matricu četvrtog reda, pronalaženje inverzne matrice korištenjem algebarskih adicija donekle je teško. No, takvih primjera ima u kontrolnim radovima.

Da biste pronašli inverznu matricu, prvo morate izračunati determinantu matrice $A$. Najbolji način za to u ovoj situaciji je proširenje determinante u nizu (stupcu). Odaberemo bilo koji redak ili stupac i pronađemo algebarski komplement svakog elementa odabranog retka ili stupca.

Na primjer, za prvi red dobivamo:

$$ A_(11)=\lijevo|\početak(niz)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \kraj(niz)\desno|=556;\; A_(12)=-\lijevo|\početak(niz)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \kraj(niz)\desno|=-300; $$ $$ A_(13)=\lijevo|\početak(niz)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \kraj(niz)\desno|=-536;\; A_(14)=-\lijevo|\početak(niz)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \kraj(niz)\desno|=-112. $$

Determinanta matrice $A$ izračunava se sljedećom formulom:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14)=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(- 112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31)=-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\ ; A_(42)=-250;\;A_(43)=-463;\;A_(44)=-96. \kraj(poravnano) $$

Algebarska komplementarna matrica: $A^*=\lijevo(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36\\ 473 & -250 & -463 & -96\end(array)\right)$.

Priložena matrica: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Inverzna matrica:

$$ A^(-1)=\frac(1)(100)\cdot \lijevo(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \ lijevo(\početak(niz) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24 / 25 \end(array) \right) $$

Provjeru, po želji, možete izvršiti na isti način kao u prethodnim primjerima.

Odgovor: $A^(-1)=\lijevo(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/ 25 & 9/25 & -24/25 \end(array) \right)$.

U drugom dijelu razmatrat će se još jedan način pronalaženja inverzne matrice koji uključuje korištenje transformacija Gaussove metode ili Gauss-Jordanove metode.

Neka je dana kvadratna matrica. Potrebno je pronaći inverznu matricu.

Prvi način. U teoremu 4.1 o postojanju i jedinstvenosti inverzne matrice naznačen je jedan od načina njezina pronalaženja.

1. Izračunajte determinantu zadane matrice. Ako, tada inverzna matrica ne postoji (matrica je degenerirana).

2. Sastavite matricu od algebarskih komplemenata elemenata matrice.

3. Transponiranjem matrice dobiva se pridružena matrica .

4. Nađite inverznu matricu (4.1) dijeljenjem svih elemenata pridružene matrice s determinantom

Drugi način. Za pronalaženje inverzne matrice mogu se koristiti elementarne transformacije.

1. Sastavite blok matricu dodjeljivanjem zadanoj matrici matrice identiteta istog reda.

2. Uz pomoć elementarnih transformacija izvedenih na redovima matrice, dovedite njen lijevi blok u najjednostavniji oblik. U ovom slučaju, blok matrica se reducira na oblik, gdje je kvadratna matrica dobivena kao rezultat transformacija iz matrice identiteta.

3. Ako je , tada je blok jednak inverznoj matrici, tj. Ako, tada matrica nema inverza.

Doista, uz pomoć elementarnih transformacija redaka matrice, njen lijevi blok može se svesti na pojednostavljeni oblik (vidi sliku 1.5). U ovom slučaju, blok matrica se transformira u oblik, gdje je elementarna matrica koja zadovoljava jednakost. Ako je matrica nesingularna, tada se, prema točki 2. napomene 3.3, njezin pojednostavljeni oblik podudara s matricom identiteta. Tada iz jednakosti slijedi da. Ako je matrica degenerirana, tada se njezin pojednostavljeni oblik razlikuje od matrice identiteta, a matrica nema inverz.

11. Matrične jednadžbe i njihovo rješenje. Matrična notacija SLAE. Matrična metoda (metoda inverzne matrice) za rješavanje SLAE i uvjeti njene primjenjivosti.

Matrične jednadžbe su jednadžbe oblika: A*X=C; X*A=C; A*X*B=C gdje su matrice A, B, C poznate, matrica X nije poznata, ako matrice A i B nisu degenerirane, tada će rješenja izvornih matrica biti zapisana u odgovarajućem obliku: X=A -1 *C; X=C*A -1; X \u003d A -1 * C * B -1 Matrični oblik zapisa sustava linearnih algebarskih jednadžbi. Nekoliko matrica može biti pridruženo svakom SLAE; štoviše, sam SLAE može se napisati kao matrična jednadžba. Za SLAE (1), razmotrite sljedeće matrice:

Matrica A se zove matrica sustava. Elementi ove matrice su koeficijenti zadanog SLAE.

Matrica A˜ naziva se sustav proširene matrice. Dobiva se tako da se matrici sustava doda stupac koji sadrži slobodne članove b1,b2,...,bm. Obično je ovaj stupac odvojen okomitom linijom radi jasnoće.

Stupac matrice B naziva se matrica slobodnih članova, a matrica stupca X je matrica nepoznanica.

Koristeći gore uvedenu notaciju, SLAE (1) se može napisati u obliku matrične jednadžbe: A⋅X=B.

Bilješka

Matrice povezane sa sustavom mogu se napisati na različite načine: sve ovisi o redoslijedu varijabli i jednadžbi razmatranog SLAE. Ali u svakom slučaju, redoslijed nepoznanica u svakoj jednadžbi danog SLAE mora biti isti.

Matrična metoda je prikladna za rješavanje SLAE u kojima se broj jednadžbi podudara s brojem nepoznatih varijabli, a determinanta glavne matrice sustava je različita od nule. Ako sustav sadrži više od tri jednadžbe, pronalaženje inverzne matrice zahtijeva značajan računalni napor, stoga je u ovom slučaju preporučljivo koristiti za rješavanje Gaussova metoda.

12. Homogene SLAE, uvjeti postojanja njihovih rješenja različitih od nule. Svojstva parcijalnih rješenja homogenih SLAE.

Linearna jednadžba se naziva homogenom ako je njen slobodni član jednak nuli, a nehomogenom u suprotnom. Sustav koji se sastoji od homogenih jednadžbi naziva se homogenim i ima opći oblik:

13 .Pojam linearne neovisnosti i ovisnosti parcijalnih rješenja homogene SLAE. Temeljni sustav odlučivanja (FSR) i njegov nalaz. Prikaz općeg rješenja homogenog SLAE u smislu FSR-a.

Sustav funkcija g 1 (x ), g 2 (x ), …, g n (x ) Zove se linearno ovisna na intervalu ( a , b ) ako postoji skup konstantnih koeficijenata koji nisu jednaki nuli istovremeno, tako da je linearna kombinacija ovih funkcija identično jednaka nuli na ( a , b ): Za . Ako je jednakost za moguća samo za , sustav funkcija g 1 (x ), g 2 (x ), …, g n (x ) Zove se linearno neovisni na intervalu ( a , b ). Drugim riječima, funkcije g 1 (x ), g 2 (x ), …, g n (x ) linearno ovisna na intervalu ( a , b ) ako postoji nula na ( a , b ) njihova netrivijalna linearna kombinacija. Funkcije g 1 (x ),g 2 (x ), …, g n (x ) linearno neovisni na intervalu ( a , b ) ako je samo njihova trivijalna linearna kombinacija identično jednaka nuli na ( a , b ).

Temeljni sustav odlučivanja (FSR) homogena SLAE osnova je ovog sustava stupova.

Broj elemenata u FSR jednak je broju nepoznanica u sustavu umanjenom za rang matrice sustava. Svako rješenje izvornog sustava je linearna kombinacija rješenja FSR-a.

Teorema

Opće rješenje nehomogenog SLAE jednako je zbroju partikularnog rješenja nehomogenog SLAE i općeg rješenja odgovarajućeg homogenog SLAE.

1 . Ako su stupci rješenja homogenog sustava jednadžbi, tada je svaka njihova linearna kombinacija također rješenje homogenog sustava.

Doista, iz jednakosti slijedi da

oni. linearna kombinacija rješenja je rješenje homogenog sustava.

2. Ako je rang matrice homogenog sustava , tada sustav ima linearno neovisna rješenja.

Doista, pomoću formula (5.13) općeg rješenja homogenog sustava možemo pronaći posebna rješenja pridjeljujući sljedeće slobodnim varijablama setovi zadanih vrijednosti (svaki put uz pretpostavku da je jedna od slobodnih varijabli jednaka jedinici, a ostale su jednake nuli):

koji su linearno neovisni. Doista, ako je matrica formirana iz ovih stupaca, tada njeni posljednji redovi tvore matricu identiteta. Dakle, minor koji se nalazi u posljednjim redovima nije jednak nuli (jednak je jedinici), tj. je osnovni. Stoga će rang matrice biti jednak. Stoga su svi stupci ove matrice linearno neovisni (vidi teorem 3.4).

Svaka zbirka linearno neovisnih rješenja homogenog sustava naziva se temeljni sustav (skup) rješenja .

14 Minor th reda, osnovni mol, rang matrice. Izračun ranga matrice.

Red k minor matrice A je determinanta neke od njezinih kvadratnih submatrica reda k.

U m x n matrici A, minor reda r naziva se bazičnim ako je različit od nule, a svi minori većeg reda, ako postoje, jednaki su nuli.

Stupci i redovi matrice A, u čijem sjecištu se nalazi baza minor, nazivaju se baznim stupcima i redovima matrice A.

Teorem 1. (O rangu matrice). Za svaku matricu, sporedni rang jednak je rangu retka i jednak rangu stupca.

Teorem 2. (O osnovnom minoru). Svaki stupac matrice rastavljen je u linearnu kombinaciju svojih osnovnih stupaca.

Rang matrice (ili manji rang) je red baznog minora ili, drugim riječima, najveći red za koji postoje minori različiti od nule. Rang nulte matrice se, po definiciji, smatra 0.

Primjećujemo dva očita svojstva manjeg ranga.

1) Rang matrice se ne mijenja prilikom transponiranja, jer kada se matrica transponira, sve njene submatrice se transponiraju, a minori se ne mijenjaju.

2) Ako je A' podmatrica matrice A, tada rang A' ne prelazi rang A, budući da je minor različit od nule uključen u A' također uključen u A.

15. Pojam -dimenzionalnog aritmetičkog vektora. Vektorska jednakost. Radnje na vektorima (zbrajanje, oduzimanje, množenje brojem, množenje matricom). Linearna kombinacija vektora.

Naručeno preuzimanje n realni ili kompleksni brojevi se zove n-dimenzionalni vektor. Brojevi se nazivaju vektorske koordinate.

Dva vektora (različita od nule). a I b jednaki ako su jednakosmjerni i imaju isti modul. Svi nulti vektori se smatraju jednakima. U svim ostalim slučajevima vektori nisu jednaki.

Zbrajanje vektora. Postoje dva načina zbrajanja vektora.1. pravilo paralelograma. Da bismo dodali vektore i, postavljamo ishodišta oba u istu točku. Dovršavamo paralelogram i iz iste točke povlačimo dijagonalu paralelograma. Ovo će biti zbroj vektora.

2. Drugi način zbrajanja vektora je pravilo trokuta. Uzmimo iste vektore i . Na kraj prvog vektora dodajemo početak drugog. Sada spojimo početak prve i kraj druge. Ovo je zbroj vektora i . Prema istom pravilu, možete dodati nekoliko vektora. Pričvršćujemo ih jedan po jedan, a zatim povezujemo početak prvog s krajem posljednjeg.

Oduzimanje vektora. Vektor je usmjeren suprotno od vektora. Duljine vektora su jednake. Sada je jasno što je oduzimanje vektora. Razlika vektora i je zbroj vektora i vektora .

Pomnožite vektor s brojem

Množenje vektora s brojem k rezultira vektorom čija je duljina k puta različita od duljine. Istosmjeran je s vektorom ako je k veći od nule, a suprotno usmjeren ako je k manji od nule.

Skalarni umnožak vektora umnožak je duljina vektora i kosinusa kuta između njih. Ako su vektori okomiti, njihov točkasti produkt je nula. I ovako se skalarni umnožak izražava preko koordinata vektora i .

Linearna kombinacija vektora

Linearna kombinacija vektora vektor poziva

Gdje - koeficijenti linearne kombinacije. Ako kombinacija se naziva trivijalnom ako je netrivijalna.

16 .Skalarni produkt aritmetičkih vektora. Duljina vektora i kut između vektora. Pojam ortogonalnosti vektora.

Skalarni produkt vektora a i b je broj

Skalarni umnožak služi za izračunavanje: 1) pronalaženje kuta između njih; 2) pronalaženje projekcije vektora; 3) izračunavanje duljine vektora; 4) uvjet okomitosti vektora.

Duljina dužine AB je udaljenost između točaka A i B. Kut između vektora A i B naziva se kut α = (a, c), 0≤ α ≤P. Pri čemu je potrebno rotirati 1 vektor tako da se njegov smjer poklapa s drugim vektorom. Pod uvjetom da im se počeci podudaraju.

Orth a je vektor a koji ima jediničnu duljinu i smjer a.

17. Sustav vektora i njegova linearna kombinacija. Pojam linearne ovisnosti i neovisnosti sustava vektora. Teorem o potrebnim i dovoljnim uvjetima linearne ovisnosti sustava vektora.

Sustav vektora a1,a2,...,an nazivamo linearno ovisnim ako postoje brojevi λ1,λ2,...,λn takvi da je barem jedan od njih različit od nule i λ1a1+λ2a2+...+λnan=0. Inače se sustav naziva linearno neovisnim.

Dva vektora a1 i a2 nazivamo kolinearnima ako su im smjerovi jednaki ili suprotni.

Tri vektora a1,a2 i a3 nazivamo komplanarnima ako su paralelna s nekom ravninom.

Geometrijski kriteriji za linearnu ovisnost:

a) sustav (a1,a2) je linearno ovisan ako i samo ako su vektori a1 i a2 kolinearni.

b) sustav (a1,a2,a3) je linearno ovisan ako i samo ako su vektori a1,a2 i a3 koplanarni.

teorema. (Potreban i dovoljan uvjet za linearnu ovisnost sustava vektori.)

Vektorski sustav vektor prostor je linearno ovisan ako i samo ako je jedan od vektora sustava linearno izražen kroz ostale vektor ovaj sustav.

Posljedica.1. Sustav vektora u vektorskom prostoru je linearno neovisan ako i samo ako nijedan od vektora sustava nije linearno izražen preko drugih vektora ovog sustava.2. Vektorski sustav koji sadrži nulti vektor ili dva jednaka vektora je linearno ovisan.