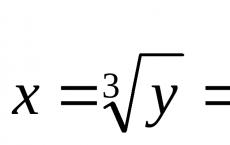Tekintsük a sokszöget, hogy milyen alakzatokra van felosztva. Szabályos sokszög

Mit nevezünk sokszögnek? A sokszögek típusai. POLYGON, lapos geometriai alakzat, amelynek három vagy több oldala három vagy több pontban (csúcsban) metszi egymást. Meghatározás. A sokszög minden oldalról zárt szaggatott vonallal határolt geometriai alakzat, amely három vagy több szakaszból (linkből) áll. A háromszög határozottan sokszög. A sokszög olyan alakzat, amelynek öt vagy több szöge van.

Meghatározás. A négyszög egy lapos geometriai alakzat, amely négy pontból (a négyszög csúcsaiból) és négy egymást követő, ezeket összekötő szakaszból (a négyszög oldalaiból) áll.

A téglalap olyan négyszög, amelynek minden derékszöge van. Az oldalak vagy csúcsok száma szerint nevezik el őket: TRIANGLE (háromoldalú); QUADAGON (négyoldalas); PENTAGON (ötoldalas) stb. Az elemi geometriában egy alakzatot egyenes vonalakkal határolt alaknak nevezünk, amelyet oldalaknak nevezünk. Azokat a pontokat, ahol az oldalak metszik, csúcsoknak nevezzük. Egy sokszögnek háromnál több szöge van. Ezt elfogadják vagy elfogadják.

A háromszög háromszög. És a négyszög szintén nem sokszög, és nem is nevezik négyszögnek - ez vagy négyzet, rombusz vagy trapéz. Az a tény, hogy a három oldalú és három szögű sokszög saját "háromszög" elnevezéssel rendelkezik, nem fosztja meg sokszög státuszától.

Nézze meg, mi a „POLYGON” más szótárakban:

Megtudjuk, hogy ezt az ábrát egy zárt szaggatott vonal határolja, ami viszont lehet egyszerű, zárt. Beszéljünk arról, hogy a sokszögek lehetnek laposak, szabályosak vagy konvexek. Ki ne hallott volna a titokzatos Bermuda-háromszögről, amelyben hajók és repülők tűnnek el nyomtalanul? De a háromszög, amelyet gyermekkorunkból ismerünk, tele van sok érdekes és titokzatos dologgal.

Bár természetesen sokszögnek tekinthető a három szögből álló figura is

De ez nem elég az alak jellemzéséhez. Az A1A2...An szaggatott vonal az A1,A2,...An pontokból és az ezeket összekötő A1A2, A2A3,... szakaszokból álló ábra. Egy egyszerű zárt szaggatott vonalat sokszögnek nevezünk, ha szomszédos láncszemei ​​nem ugyanazon az egyenesen fekszenek (5. ábra). Helyettesíts be egy adott számot, például 3-at a „sokszög” szóba a „sok” szó helyett, így egy háromszöget kapunk. Vegyük észre, hogy ahány szög van, annyi oldala van, ezért ezeket az alakzatokat sokoldalúnak nevezhetjük.

Legyen A1A2...A n egy adott konvex sokszög és n>3. Rajzoljunk bele átlókat (egy csúcsból)

Mindegyik háromszög szögeinek összege 1800, és ezeknek az n háromszögeknek a száma 2. Ezért a konvex n - A1A2...A n háromszög szögeinek összege 1800* (n - 2). A tétel bizonyítást nyert. Egy konvex sokszög külső szöge egy adott csúcsban a sokszög belső szögével szomszédos szög ebben a csúcsban.

Egy négyszögben húzz egy egyenest úgy, hogy az három háromszögre osztja

Egy négyszögnek soha nincs három csúcsa ugyanazon az egyenesen. A „sokszög” szó azt jelzi, hogy a család minden alakjának „sok szöge van”. A szaggatott vonalat egyszerűnek nevezzük, ha nincs önálló metszéspontja (2., 3. ábra).

A szaggatott vonal hossza a láncszemei ​​hosszának összege (4. ábra). n=3 esetben a tétel érvényes. Tehát a négyzetet másképp nevezhetjük - szabályos négyszögnek. Az ilyen figurák régóta érdeklik az épületeket díszítő kézműveseket.

A csúcsok száma megegyezik az oldalak számával. Egy vonalláncot zártnak nevezünk, ha a végei egybeesnek. Ők csinálták gyönyörű minták, például parkettára. Ötágú csillagunk szabályos ötszögletű csillag.

De nem minden szabályos sokszögből lehetett parkettát készíteni. Nézzünk meg közelebbről kétféle sokszöget: a háromszöget és a négyszöget. Szabályosnak nevezzük azt a sokszöget, amelyben minden belső szög egyenlő. A sokszögeket az oldalak vagy csúcsok száma alapján nevezik el.

Ebben a leckében egy új témát kezdünk, és egy új fogalmat vezetünk be számunkra: „sokszög”. Megnézzük a sokszögekhez kapcsolódó alapfogalmakat: oldalak, csúcsszögek, konvexitás és nemkonvexitás. Aztán bebizonyítjuk a legfontosabb tényeket, mint például a sokszög belső szögeinek összegére vonatkozó tétel, a sokszög külső szögeinek összegére vonatkozó tétel. Ennek eredményeként közel kerülünk a sokszögek speciális eseteinek tanulmányozásához, amelyekről a további leckékben szó lesz.

Téma: Négyszögek

Tanulság: Sokszögek

A geometria tanfolyamon a geometriai alakzatok tulajdonságait tanulmányozzuk, és már megvizsgáltuk a legegyszerűbbeket: a háromszögeket és a köröket. Ugyanakkor tárgyaltuk ezen alakzatok speciális speciális eseteit is, mint például a jobb oldali, az egyenlő szárú és a szabályos háromszögek. Itt az ideje, hogy általánosabb és összetettebb számokról beszéljünk - sokszögek.

Különleges tokkal sokszögek már ismerjük – ez egy háromszög (lásd 1. ábra).

Rizs. 1. Háromszög

Már maga a név is hangsúlyozza, hogy ez egy háromszögű figura. Ezért be poligon sok lehet belőlük, pl. több mint három. Például rajzoljunk egy ötszöget (lásd 2. ábra), azaz. öt sarkú figura.

Rizs. 2. Pentagon. Konvex sokszög

Meghatározás.Poligon- több pontból (kettőnél több) és megfelelő számú szegmensből álló ábra, amelyek egymás után összekötik őket. Ezeket a pontokat ún csúcsok sokszög, és a szakaszok a felek. Ebben az esetben nincs két szomszédos oldal ugyanazon az egyenesen, és nincs két nem szomszédos oldal sem metszi egymást.

Meghatározás.Szabályos sokszög egy konvex sokszög, amelyben minden oldal és szög egyenlő.

Bármi poligon két részre osztja a síkot: belső és külső. A belső területet más néven poligon.

Más szóval, amikor például egy ötszögről beszélnek, akkor a teljes belső régióját és a határát is jelentik. A belső régió pedig magában foglalja az összes olyan pontot, amely a sokszög belsejében található, azaz. a pont az ötszögre is utal (lásd 2. ábra).

A sokszögeket néha n-szögeknek is nevezik, hogy hangsúlyozzák, hogy bizonyos ismeretlen számú szög (n darab) előfordulásának általános esetét vesszük figyelembe.

Meghatározás. Sokszög kerülete- a sokszög oldalai hosszának összege.

Most meg kell ismerkednünk a sokszögek típusaival. Osztva vannak konvexÉs nem domború. Például az ábrán látható sokszög. A 2. ábra konvex, és a 2. ábrán látható. 3 nem domború.

Rizs. 3. Nem konvex sokszög

1. definíció. Poligon hívott konvex, ha bármelyik oldalán keresztül egyenes vonal húzásakor a teljes poligon ennek az egyenesnek csak az egyik oldalán fekszik. Nem domború mindenki más sokszögek.

Könnyen elképzelhető, hogy az ötszög bármely oldalának meghosszabbításakor a 1. ábrán. 2 mindez ennek az egyenesnek az egyik oldalán lesz, azaz. domború. Ám amikor egyenes vonalat húzunk egy négyszögön keresztül az ábrán. 3 már látjuk, hogy két részre osztja, i.e. nem domború.

De van egy másik definíció is a sokszög konvexitásáról.

2. definíció. Poligon hívott konvex, ha bármely két belső pontjának kiválasztásakor és egy szegmenssel összekötve a szakasz minden pontja egyben a sokszög belső pontja is.

Ennek a definíciónak a használatának szemléltetése látható a szegmensek felépítésének példáján az ábrán. 2. és 3.

Meghatározás. Átlós A sokszög bármely szakasza, amely két nem szomszédos csúcsot köt össze.

A sokszögek tulajdonságainak leírására két legfontosabb tétel van a szögeikről: tétel egy konvex sokszög belső szögeinek összegérőlÉs tétel egy konvex sokszög külső szögeinek összegéről. Nézzük meg őket.

Tétel. Egy konvex sokszög belső szögeinek összegéről (n-gon).

Hol van a szögeinek (oldalainak) száma.

1. bizonyítás. Ábrázoljuk az ábrán. 4 konvex n-szög.

Rizs. 4. Konvex n-szög

A csúcsból kirajzoljuk az összes lehetséges átlót. Az n-szöget háromszögekre osztják, mert a sokszög minden oldala egy háromszöget alkot, kivéve a csúcsgal szomszédos oldalakat. Az ábrán jól látható, hogy ezen háromszögek szögeinek összege pontosan egyenlő lesz az n-szög belső szögeinek összegével. Mivel bármely háromszög szögeinek összege , akkor egy n-szög belső szögeinek összege:

Q.E.D.

2. bizonyítás. Ennek a tételnek egy másik bizonyítása is lehetséges. Rajzoljunk egy hasonló n-szöget az ábrán. 5, és csatlakoztassa bármelyik belső pontját az összes csúcshoz.

Rizs. 5.

Megkaptuk az n-szög n háromszögre való felosztását (annyi oldala van a háromszögeknek). Az összes szögük összege egyenlő a sokszög belső szögeinek összegével és a belső pont szögeinek összegével, és ez a szög. Nekünk van:

Q.E.D.

Igazolt.

A bizonyított tétel szerint világos, hogy egy n-szög szögeinek összege függ oldalainak számától (n-en). Például egy háromszögben, és a szögek összege . Egy négyszögben, és a szögek összege stb.

Tétel. Egy konvex sokszög külső szögeinek összegéről (n-gon).

Hol van a szögeinek (oldalainak) száma, és , …, a külső szögek.

Bizonyíték. Ábrázoljunk egy konvex n-szöget az ábrán. 6, és jelölje ki belső és külső szögeit.

Rizs. 6. Konvex n-szög meghatározott külső szögekkel

Mert A külső sarok tehát szomszédosként csatlakozik a belsőhöz és hasonlóan a fennmaradó külső sarkokhoz. Akkor:

A transzformációk során az n-szög belső szögeinek összegére vonatkozó, már bevált tételt alkalmaztuk.

Igazolt.

A bizonyított tételből az következik Érdekes tény, hogy egy konvex n-szög külső szögeinek összege egyenlő szögeinek (oldalainak) számáról. Egyébként a belső szögek összegével ellentétben.

Bibliográfia

1. Alexandrov A.D. és mások Geometria, 8. osztály. - M.: Oktatás, 2006.
2. Butuzov V.F., Kadomtsev S.B., Prasolov V.V. Geometria, 8. osztály. - M.: Oktatás, 2011.
3. Merzlyak A.G., Polonsky V.B., Yakir S.M. Geometria, 8. osztály. - M.: VENTANA-GRAF, 2009.

1. Profmeter.com.ua ().
2. Narod.ru ().
3. Xvatit.com ().

Házi feladat

1. § A háromszög fogalma

Ebben a leckében olyan alakzatokat ismerhet meg, mint a háromszögek és sokszögek.

Ha három nem ugyanazon az egyenesen lévő pontot szakaszokkal kötünk össze, akkor háromszöget kapunk. A háromszögnek három csúcsa és három oldala van.

Mielőtt te lennél egy ABC háromszög, három csúcsa van (A pont, B pont és C pont) és három oldala (AB, AC és CB).

Egyébként ugyanazokat az oldalakat másképp nevezhetjük:

AB=BA, AC=SA, CB=BC.

A háromszög oldalai három szöget zárnak be a háromszög csúcsainál. Az ábrán A szög, B szög, C szög látható.

Így a háromszög egy geometriai alakzat, amelyet három szakasz köt össze, amelyek három pontot kötnek össze, amelyek nem ugyanazon az egyenesen helyezkednek el.

2. § A sokszög fogalma és típusai

A háromszögeken kívül vannak négyszögek, ötszögek, hatszögek stb. Egyszóval sokszögnek nevezhetők.

A képen a DMKE négyszög látható.

A D, M, K és E pontok a négyszög csúcsai.

A DM, MK, KE, ED szakaszok ennek a négyszögnek az oldalai. Csakúgy, mint egy háromszög esetében, a négyszög oldalai négy szöget alkotnak a csúcsokban, ahogy sejtette, innen a név - négyszög. Ennél a négyszögnél az ábrán látható a D szög, az M szög, a K szög és az E szög.

Milyen négyszögeket ismersz már?

Négyzet és téglalap! Mindegyiknek négy sarka és négy oldala van.

A sokszög másik típusa az ötszög.

Az O, P, X, Y, T pontok az ötszög csúcsai, a TO, OP, PX, XY, YT szakaszok pedig ennek az ötszögnek az oldalai. Az ötszögnek öt szöge és öt oldala van.

Mit gondol, hány szöge és hány oldala van egy hatszögnek? Így van, hat! Hasonló módon érvelve megmondhatjuk, hogy egy adott sokszögnek hány oldala, csúcsa vagy szöge van. És arra a következtetésre juthatunk, hogy a háromszög is sokszög, amelynek pontosan három szöge, három oldala és három csúcsa van.

Így ebben a leckében olyan fogalmakat ismerhetett meg, mint a háromszög és a sokszög. Megtudtuk, hogy egy háromszögnek 3 csúcsa, 3 oldala és 3 szöge van, a négyszögnek 4 csúcsa, 4 oldala és 4 szöge, az ötszögnek 5 oldala, 5 csúcsa, 5 szöge stb.

A felhasznált irodalom listája:

1. Matematika 5. osztály. Vilenkin N.Ya., Zhokhov V.I. és mások. 31. kiadás, törölve. - M: 2013.
2. Didaktikai anyagok matematikához 5. osztály. Szerző - Popov M.A. - 2013-as év
3. Hiba nélkül számolunk. Önellenőrzéssel végzett munka matematika 5-6. évfolyamon. Szerző - Minaeva S.S. - 2014-es év
4. Didaktikai anyagok matematikához 5. osztály. Szerzők: Dorofeev G.V., Kuznetsova L.V. - 2010
5. Matematika tesztek és önálló munkavégzés 5. évfolyam. Szerzők - Popov M.A. - 2012-es év
6. Matematika. 5. évfolyam: oktatási. általános iskolai tanulók számára. intézmények / I. I. Zubareva, A. G. Mordkovich. - 9. kiadás, törölve. - M.: Mnemosyne, 2009

A sík zárt szaggatott vonallal határolt részét sokszögnek nevezzük.

Ennek a szaggatott vonalnak a szakaszait ún a felek poligon. AB, BC, CD, DE, EA (1. ábra) az ABCDE sokszög oldalai. Egy sokszög összes oldalának összegét nevezzük annak kerülete.

A sokszög ún konvex, ha bármelyik oldalának egyik oldalán helyezkedik el, határozatlanul kiterjesztve mindkét csúcson túlra.

Az MNPKO sokszög (1. ábra) nem lesz konvex, mivel a KR egyenes több mint egy oldalán található.

Csak a konvex sokszögeket fogjuk figyelembe venni.

A sokszög két szomszédos oldala által alkotott szögeket sokszögének nevezzük belső sarkai, és a tetejük a sokszög csúcsai.

A sokszög két nem szomszédos csúcsát összekötő egyenes szakaszt a sokszög átlójának nevezzük.

AC, AD - a sokszög átlói (2. ábra).

A sokszög belső szögeivel szomszédos szögeket a sokszög külső szögeinek nevezzük (3. ábra).

A sokszöget a szögek (oldalak) számától függően háromszögnek, négyszögnek, ötszögnek stb.

Két sokszöget akkor mondunk egybevágónak, ha átfedéssel összehozhatók.

Beírt és körülírt sokszögek

Ha egy sokszög minden csúcsa egy körön fekszik, akkor a sokszöget hívjuk felírva egy körbe, és a kör - leírta a sokszög közelében (ábra).

Ha egy sokszög minden oldala érinti a kört, akkor a sokszöget nevezzük leírta egy körről, és a kört ún felírva sokszögbe (ábra).

Sokszögek hasonlósága

Két azonos nevű sokszöget hasonlónak nevezünk, ha az egyik szöge egyenlő a másik szögeivel, és a sokszögek hasonló oldalai arányosak.

Az azonos számú oldallal (szögekkel) rendelkező sokszögeket azonos nevű sokszögeknek nevezzük.

A megfelelően egyenlő szögű csúcsokat összekötő hasonló sokszögek oldalait hasonlónak nevezzük (ábra).

Tehát például ahhoz, hogy az ABCDE sokszög hasonló legyen az A'B'C'D'E' sokszöghez, szükséges, hogy: ∠A = ∠A' ∠B = ∠B' ∠C = ∠C' ∠ D = ∠D' ∠ E = ∠E' és ezen kívül AB / A'B' = BC / B'C' = CD / C'D' = DE / D'E' = EA / E'A' .

Hasonló sokszögek kerületeinek aránya

Először is vegyük figyelembe az egyenlő arányok sorozatának tulajdonságát. Legyen például a következő arányok: 2 / 1 = 4 / 2 = 6 / 3 = 8 / 4 =2.

Határozzuk meg ezen relációk előző tagjainak összegét, majd a következő tagok összegét, és keressük meg a kapott összegek arányát, kapjuk:

$$ \frac(2 + 4 + 6 + 8)(1 + 2 + 3 + 4) = \frac(20)(10) = 2 $$

Ugyanezt kapjuk, ha egy sor más összefüggést veszünk, például: 2 / 3 = 4 / 6 = 6 / 9 = 8 / 12 = 10 / 15 = 2 / 3 Keressük meg az előző tagok összegét. ezeket az összefüggéseket és a rákövetkezők összegét, majd megkeresve ezeknek az összegeknek az arányát, kapjuk:

$$ \frac(2 + 4 + 5 + 8 + 10)(3 + 6 + 9 + 12 + 15) = \frac(30)(45) = \frac(2)(3) $$

Mindkét esetben az egyenlő relációk sorozatának előző tagjainak összege ugyanazon sorozat következő tagjainak összegére vonatkozik, mint ahogy ezen relációk bármelyikének előző tagja a következőre vonatkozik.

Ezt a tulajdonságot számos numerikus példából származtattuk. Szigorúan és általános formában származtatható.

Most vegyük figyelembe a hasonló sokszögek kerületének arányát.

Legyen az ABCDE sokszög hasonló az A’B’C’D’E’ sokszöghez (ábra).

E sokszögek hasonlóságából az következik

AB / A’B’ = BC / B’C’ = CD / C’D’ = DE / D’E’ = EA / E’A’

Az egyenlő arányok sorozatára levezetett tulajdonság alapján felírhatjuk:

Az általunk felvett összefüggések előző tagjainak összege az első sokszög kerületét (P), ezen relációk következő tagjainak összege pedig a második sokszög kerületét (P'), ami P / P-t jelent. ' = AB / A'B'.

Ennélfogva, A hasonló sokszögek kerületei a hasonló oldalukhoz kapcsolódnak.

Hasonló sokszögek területének aránya

Legyenek ABCDE és A’B’C’D’E’ hasonló sokszögek (ábra).

Ismeretes, hogy ΔАВС ~ ΔA'В'С' ΔACD ~ ΔA'C'D' és ΔADE ~ ΔA'D'E'.

Kívül,

;

Mivel ezeknek az arányoknak a második arányai egyenlőek, ami a sokszögek hasonlóságából következik, akkor

Az egyenlő arányok sorozatának tulajdonságát felhasználva kapjuk:

Vagy

ahol S és S’ ezeknek a hasonló sokszögeknek a területei.

Ennélfogva, A hasonló sokszögek területei a hasonló oldalak négyzeteihez kapcsolódnak.

A kapott képlet a következő formára konvertálható: S / S’ = (AB / A’B’) 2

Egy tetszőleges sokszög területe

Legyen szükséges egy tetszőleges ABC négyszög területének kiszámítása (ábra).

Rajzoljunk bele egy átlót, például AD. Két ABD és ACD háromszöget kapunk, amelyek területeit ki tudjuk számítani. Ezután megtaláljuk e háromszögek területének összegét. A kapott összeg ennek a négyszögnek a területét fejezi ki.

Ha ki kell számítania egy ötszög területét, akkor ugyanezt tesszük: átlókat rajzolunk az egyik csúcsból. Három háromszöget kapunk, amelyek területét ki tudjuk számítani. Ez azt jelenti, hogy meg tudjuk találni ennek az ötszögnek a területét. Ugyanezt tesszük bármely sokszög területének kiszámításakor.

Egy sokszög vetített területe

Emlékezzünk vissza, hogy az egyenes és a sík közötti szög az adott egyenes és a síkra való vetülete közötti szög (ábra).

Tétel. A sokszög síkra merőleges vetületének területe egyenlő a kivetített sokszög területével, megszorozva a sokszög síkja és a vetítési sík által alkotott szög koszinuszával.

Minden sokszög háromszögekre osztható, amelyek területeinek összege megegyezik a sokszög területével. Ezért egy háromszögre elegendő bebizonyítani a tételt.

Legyen ΔАВС a síkra vetítve R. Nézzünk két esetet:

a) az egyik ΔABC oldal párhuzamos a síkkal R;

b) egyik ΔABC oldal sem párhuzamos R.

Mérlegeljük első eset: legyen [AB] || R.

Rajzoljunk egy síkot (AB) keresztül! R 1 || Rés a ΔАВС ortogonálisan vetítjük be R 1 és tovább R(rizs.); ΔАВС 1-et és ΔА'В'С'-t kapunk.

A projekció tulajdonsága alapján ΔАВС 1 (cong) ΔА'В'С', ezért

S Δ ABC1 = S Δ A’B’C’

Rajzoljuk ⊥ és a D 1 C 1 szakaszt. Ekkor ⊥, a \(\overbrace(CD_1C_1)\) = φ az ΔABC sík és a sík közötti szög értéke R 1 . Ezért

S Δ ABC1 = 1/2 | AB | | C 1 D 1 | = 1/2 | AB | | CD 1 | cos φ = S Δ ABC cos φ

és ezért S Δ A’B’C’ = S Δ ABC cos φ.

Folytassuk a mérlegelést második eset. Rajzoljunk egy síkot R 1 || R azon a ΔАВС csúcson keresztül, amely távolság a síktól R a legkisebb (legyen ez az A csúcs).

Vetítsük ki a ΔАВС-t a gépen R 1 és R(rizs.); vetületei legyenek ΔАВ 1 С 1, illetve ΔА'В'С'.

Legyen (BC) ∩ p 1 = D. Akkor

S Δ A’B’C’ = S ΔAB1 C1 = S ΔADC1 - S ΔADB1 = (S ΔADC - S ΔADB) cos φ = S Δ ABC cos φ

Más anyagok