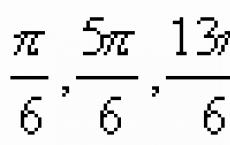Inverzné goniometrické funkcie a ich grafy. Čo je arczín, arkkozín? Čo je arkus tangens, arkus tangens? Článkové inverzné goniometrické funkcie

V mnohých úlohách matematiky a jej aplikácií je potrebné zo známej hodnoty goniometrickej funkcie nájsť zodpovedajúcu hodnotu uhla vyjadrenú v stupňoch alebo radiánoch. Je známe, že rovnaká hodnota sínusu zodpovedá nekonečnému počtu uhlov, napríklad ak $\sin α=1/2,$, potom sa uhol $α$ môže rovnať $30°$ aj $150°, $ alebo v radiánových mierach $π /6$ a $5π/6,$ a ktorýkoľvek z uhlov získaných z týchto uhlov pridaním člena v tvare $360°⋅k,$ alebo $2πk,$, kde $k$ je ľubovoľný celé číslo. Toto je zrejmé z grafu funkcie $y=\sin x$ na celej číselnej osi (pozri obr. $1$): ak na osi $Oy$ nakreslíme segment dĺžky $1/2$ a nakreslíme priamka rovnobežná s osou $Ox, $ potom pretína sínusoidu v nekonečnom počte bodov. Aby sa predišlo možnej rozmanitosti odpovedí, zavádzajú sa inverzné goniometrické funkcie, inak nazývané kruhové alebo oblúkové funkcie (z latinského slova arcus – „oblúk“).

Štyri základné goniometrické funkcie $\sin x,$ $\cos x,$ $\mathrm(tg)\,x$ a $\mathrm(ctg)\,x$ zodpovedajú štyrom oblúkovým funkciám $\arcsin x,$ $\arccos x ,$ $\mathrm(arctg)\,x$ a $\mathrm(arcctg)\,x$ (čítaj: arcsínus, arkozínus, arctangens, arckotangens). Uvažujme o funkciách \arcsin x a \mathrm(arctg)\,x, keďže ostatné dve sú v nich vyjadrené vzorcami:

$\arccos x = \frac(π)(2) − \arcsin x,$ $\mathrm(arcctg)\,x = \frac(π)(2) − \mathrm(arctg)\,x.$

Rovnosť $y = \arcsin x$ podľa definície znamená taký uhol $y,$ vyjadrený v radiáne a zahrnutý v rozsahu od $−\frac(π)(2)$ do $\frac(π)(2) ,$ sínus, ktorý sa rovná $x,$ t.j. $\sin y = x.$ Funkcia $\arcsin x$ je inverzná funkcia funkcie $\sin x,$ uvažovaná na intervale $\left[−\ frac(π)(2 ),+\frac(π)(2)\vpravo],$ kde táto funkcia monotónne rastie a nadobúda všetky hodnoty od $−1$ do $+1.$ Je zrejmé, že argument $y$ funkcie $\arcsin x$ môže nadobúdať hodnoty len zo segmentu $\left[−1,+1\right].$ Na segmente je teda definovaná funkcia $y=\arcsin x$ $\left[−1,+1\right],$ monotónne rastie a jeho hodnoty vypĺňajú segment $\left[−\frac(π)(2),+\frac(π)(2)\ vpravo].$ Graf funkcie je znázornený na obr. $ 2, $

Za podmienky $−1 ≤ a ≤ 1$ reprezentujeme všetky riešenia rovnice $\sin x = a$ ako $x=(−1)^n \arcsin a + πn,$ $n=0,±1 ,± 2, … .$ Napríklad, ak

$\sin x = \frac(\sqrt(2))(2)$ potom $x = (−1)^n \frac(π)(4)+πn,$ $n = 0, ±1, ±2 , … .$

Vzťah $y=\mathrm(arcctg)\,x$ je definovaný pre všetky hodnoty $x$ a podľa definície znamená, že uhol $y,$ vyjadrený v radiáne je v rámci

$−\frac(π)(2)

a dotyčnica tohto uhla je x, t.j. $\mathrm(tg)\,y = x.$ Funkcia $\mathrm(arctg)\,x$ je definovaná na celej reálnej čiare, je inverznou funkciou funkcie $\mathrm( tg)\,x$, ktorý sa berie do úvahy len na intervale

$−\frac(π)(2)

Funkcia $y = \mathrm(arctg)\,x$ je monotónne rastúca, jej graf je uvedený na obr. $ 3, $

Všetky riešenia rovnice $\mathrm(tg)\,x = a$ možno zapísať ako $x=\mathrm(arctg)\,a+πn,$ $n=0,±1,±2,… .$

Všimnite si, že inverzné goniometrické funkcie sú široko používané v matematickej analýze. Napríklad jedna z prvých funkcií, pre ktorú sa získalo zobrazenie nekonečného mocninového radu, bola funkcia $\mathrm(arctg)\,x.$ blízko

Úlohy súvisiace s inverznými goniometrickými funkciami sú často ponúkané na školských záverečných skúškach a na prijímacích skúškach na niektoré univerzity. Podrobné štúdium tejto témy je možné dosiahnuť len na mimoškolských hodinách alebo vo výberových predmetoch. Navrhovaný kurz je navrhnutý tak, aby čo najúplnejšie rozvíjal schopnosti každého študenta, aby sa zlepšila jeho matematická príprava.

Kurz je určený na 10 hodín:

1. Funkcie arcsin x, arccos x, arctg x, arcctg x (4 hodiny).

2. Operácie s inverznými goniometrickými funkciami (4 hodiny).

3. Inverzné goniometrické operácie na goniometrických funkciách (2 hodiny).

Lekcia 1 (2 hodiny) Téma: Funkcie y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.

Účel: úplné pokrytie tohto problému.

1. Funkcia y \u003d arcsin x.

a) Pre funkciu y \u003d sin x na segmente existuje inverzná (jednohodnotová) funkcia, ktorú sme sa dohodli na volať arcsínus a označovať ju takto: y \u003d arcsin x. Graf inverznej funkcie je symetrický s grafom hlavnej funkcie vzhľadom na os súradnicových uhlov I - III.

Vlastnosti funkcie y = arcsin x .

1) Rozsah definície: segment [-1; jeden];

2) Oblasť zmeny: rez ;

3) Funkcia y = arcsin x nepárne: arcsin (-x) = - arcsin x;

4) Funkcia y = arcsin x je monotónne rastúca;

5) Graf pretína osi Ox, Oy v počiatku.

Príklad 1. Nájdite a = arcsin . Tento príklad možno podrobne sformulovať takto: nájdite taký argument a , ležiaci v rozsahu od do , ktorého sínus sa rovná .

rozhodnutie. Existuje nespočetné množstvo argumentov, ktorých sínus je , napríklad: atď. Nás však zaujíma len argument, ktorý je na intervale . Tento argument bude. Takže, .

Príklad 2. Nájdite .rozhodnutie. Ak budeme argumentovať rovnakým spôsobom ako v príklade 1, dostaneme .

b) ústne cvičenia. Nájdite: arcsin 1, arcsin (-1), arcsin , arcsin (), arcsin , arcsin (), arcsin , arcsin (), arcsin 0 Vzorová odpoveď: , pretože . Dávajú výrazy zmysel: ; arcsin 1,5; ?

c) Usporiadajte vzostupne: arcsin, arcsin (-0,3), arcsin 0,9.

II. Funkcie y = arccos x, y = arctg x, y = arcctg x (podobne).

Lekcia 2 (2 hodiny) Téma: Inverzné goniometrické funkcie, ich grafy.

Účel: v tejto lekcii je potrebné vypracovať zručnosti pri určovaní hodnôt goniometrických funkcií, pri vykresľovaní inverzných goniometrických funkcií pomocou D (y), E (y) a potrebných transformácií.

V tejto lekcii vykonajte cvičenia, ktoré zahŕňajú nájdenie domény definície, rozsahu funkcií typu: y = arcsin , y = arccos (x-2), y = arctg (tg x), y = arccos .

Je potrebné zostaviť grafy funkcií: a) y = arcsin 2x; b) y = 2 arcsin 2x; c) y \u003d arcsin;

d) y \u003d arcsin; e) y = arcsín; f) y = arcsín; g) y = | arcsin | .

Príklad. Nakreslíme y = arccos

Do domácej úlohy môžete zahrnúť nasledujúce cvičenia: zostavte grafy funkcií: y = arccos , y = 2 arcctg x, y = arccos | x | .

Grafy inverzných funkcií

Téma lekcie č. 3 (2 hodiny):

Operácie s inverznými goniometrickými funkciami.

Účel: rozšírenie matematických vedomostí (je to dôležité pre uchádzačov o odbory so zvýšenými požiadavkami na matematickú prípravu) zavedením základných vzťahov pre inverzné goniometrické funkcie.

Lekčný materiál.

Niektoré jednoduché goniometrické operácie s inverznými goniometrickými funkciami: hriech (arcsin x) \u003d x, i xi? jeden; cos (arсcos x) = x, i xi? jeden; tg (arctg x) = x, x I R; ctg (arcctg x) = x, x I R.

Cvičenia.

a) tg (1,5 + arctg 5) = - ctg (arctg 5) = .

ctg (arctgx) = ; tg (arctgx) = .

b) cos (+ arcsin 0,6) = - cos (arcsin 0,6). Nech arcsin 0,6 \u003d a, sin a \u003d 0,6;

cos(arcsin x) = ; hriech (arccos x) = .

Poznámka: Znamienko „+“ berieme pred koreň, pretože a = arcsin x spĺňa .

c) hriech (1,5 + arcsin).Odpoveď:;

d) ctg ( + arctg 3) Odpoveď: ;

e) tg (- arcctg 4) Odpoveď: .

f) cos (0,5 + arccos) . Odpoveď: .

Vypočítať:

a) hriech (2 arctan 5) .

Nech arctg 5 = a, potom sin 2 a = alebo hriech(2 arctan 5) = ;

b) cos (+ 2 arcsin 0,8) Odpoveď: 0,28.

c) arctg + arctg.

Nech a = arctg , b = arctg ,

potom tan(a + b) = .

d) hriech (arcsin + arcsin).

e) Dokážte, že pre všetky x I [-1; 1] true arcsin x + arccos x = .

dôkaz:

arcsin x = - arccos x

sin (arcsin x) = hriech (- arccos x)

x = cos (arccos x)

Pre samostatné riešenie: sin (arccos ), cos (arcsin ) , cos (arcsin ()), sin (arctg (- 3)), tg (arccos ) , ctg (arccos ).

Pre domáce riešenie: 1) sin (arcsin 0,6 + arctg 0); 2) arcsin + arcsin; 3) ctg ( - arccos 0,6); 4) cos (2 arcctg 5); 5) hriech (1,5 - arcsin 0,8); 6) arctg 0,5 - arctg 3.

Lekcia č. 4 (2 hodiny) Téma: Operácie s inverznými goniometrickými funkciami.

Účel: v tejto lekcii ukázať použitie pomerov pri transformácii zložitejších výrazov.

Lekčný materiál.

ÚSTNE:

a) sin (arccos 0,6), cos (arcsin 0,8);

b) tg (arctg 5), ctg (arctg 5);

c) sin (arctg -3), cos (arctg ());

d) tg (arccos), ctg (arccos()).

NAPÍSANÉ:

1) cos (arcsin + arcsin + arcsin).

2) cos (arctg 5 - arccos 0,8) = cos (arctg 5) cos (arctg 0,8) + sin (arctg 5) sin (arccos 0,8) =

3) tg (- arcsin 0,6) = - tg (arcsin 0,6) =

4)

Nezávislá práca pomôže určiť úroveň asimilácie materiálu

1) tg ( arctg 2 - arctg ) 2) cos( - arctg2) 3) arcsin + arccos	1) cos (arcsin + arcsin) 2) hriech (1,5 - arctg 3) 3) arcctg3 - arctg 2

Za domácu úlohu môžete ponúknuť:

1) ctg (arctg + arctg + arctg); 2) sin 2 (arctg 2 - arcctg ()); 3) sin (2 arctg + tg ( arcsin )); 4) hriech (2 arctan); 5) tg ( (arcsin ))

Lekcia č. 5 (2h) Téma: Inverzné goniometrické operácie s goniometrickými funkciami.

Cieľ: vytvoriť u študentov pochopenie inverzných goniometrických operácií na goniometrických funkciách, zamerať sa na zvýšenie zmysluplnosti študovanej teórie.

Pri štúdiu tejto témy sa predpokladá, že množstvo teoretického materiálu na zapamätanie je obmedzené.

Materiál na lekciu:

Môžete sa začať učiť nový materiál preskúmaním funkcie y = arcsin (sin x) a jej vykreslením.

3. Každé x I R je spojené s y I, t.j.<= y <= такое, что sin y = sin x.

4. Funkcia je nepárna: sin (-x) \u003d - sin x; arcsin(sin(-x)) = - arcsin(sin x).

6. Graf y = arcsin (sin x) na:

a) 0<= x <= имеем y = arcsin(sin x) = x, ибо sin y = sin x и <= y <= .

b)<= x <= получим y = arcsin (sin x) = arcsin ( - x) = - x, ибо

sin y \u003d sin ( - x) \u003d sinx, 0<= - x <= .

takze

Po zostavení y = arcsin (sin x) na , pokračujeme symetricky okolo počiatku na [- ; 0], berúc do úvahy zvláštnosť tejto funkcie. Pomocou periodicity pokračujeme na celú číselnú os.

Potom napíšte nejaké pomery: arcsin (sin a) = ak<= a <= ; arccos (cos a ) = a ak je 0<= a <= ; arctg (tg a) = a if< a < ; arcctg (ctg a) = a , если 0 < a < .

A urobte nasledujúce cvičenia: a) arccos (sin 2) Odpoveď: 2 - ; b) arcsín (cos 0,6) Odpoveď: - 0,1; c) arctg (tg 2).Odpoveď: 2 -;

d) arcctg (tg 0,6) Odpoveď: 0,9; e) arccos (cos ( - 2)).Odpoveď: 2 -; f) arcsín (sin (- 0,6)). Odpoveď: - 0,6; g) arctg (tg 2) = arctg (tg (2 - )). Odpoveď: 2 - ; h) arcctg (tg 0,6). Odpoveď: - 0,6; - arktanx; e) arccos + arccos

Čo je arczín, arkkozín? Čo je arkus tangens, arkus tangens?

Pozor!
Existujú ďalšie
materiály v Osobitný oddiel 555.
Pre tých, ktorí silne „nie veľmi...“
A pre tých, ktorí „veľmi...“)

K pojmom arcsínus, arkozínus, arktangens, arkkotangens študentská populácia je opatrná. Nerozumie týmto pojmom, a preto neverí tejto slávnej rodine.) Ale márne. Sú to veľmi jednoduché koncepty. Čo mimochodom znalému človeku výrazne uľahčí život pri rozhodovaní goniometrické rovnice!

Máte zmätok v jednoduchosti? Márne.) Práve tu a teraz sa o tom presvedčíš.

Samozrejme, pre pochopenie by bolo dobré vedieť čo je sínus, kosínus, tangens a kotangens.áno ich tabuľkové hodnoty pre niektoré uhly... Aspoň vo všeobecnosti. Potom ani tu nebudú žiadne problémy.

Takže sme prekvapení, ale pamätajte: arksínus, arkozínus, arktangens a arctangens sú len niektoré uhly. Nie viac nie menej. Je tam uhol, povedzme 30°. A je tu uhol arcsin0.4. Alebo arctg(-1,3). Existujú všetky druhy uhlov.) Uhly môžete jednoducho písať rôznymi spôsobmi. Môžete napísať uhol z hľadiska stupňov alebo radiánov. Alebo môžete - cez jeho sínus, kosínus, tangens a kotangens ...

Čo znamená výraz

arcsin 0,4?

Toto je uhol, ktorého sínus je 0,4! Áno áno. Toto je význam arcsínusu. Opakujem konkrétne: arcsin 0,4 je uhol, ktorého sínus je 0,4.

A to je všetko.

Aby som si túto jednoduchú myšlienku udržal v hlave ešte dlho, uvediem dokonca rozpis tohto hrozného termínu - arcsínus:

oblúk hriech 0,4
injekcia, ktorých sínus rovná sa 0,4

Ako sa píše, tak sa počúva.) Skoro. Predpona oblúk znamená oblúk(slov arch viete?), pretože starí ľudia používali namiesto rohov oblúky, ale to nič nemení na podstate veci. Pamätajte na toto základné dekódovanie matematického pojmu! Navyše, pre arkus-kosínus, arkus tangens a arkus tangens sa dekódovanie líši iba v názve funkcie.

Čo je arccos 0,8?
Toto je uhol, ktorého kosínus je 0,8.

Čo je arctan(-1,3)?
Toto je uhol, ktorého dotyčnica je -1,3.

Čo je arcctg 12?
Toto je uhol, ktorého kotangens je 12.

Takéto elementárne dekódovanie mimochodom umožňuje vyhnúť sa epickým chybám.) Napríklad výraz arccos1,8 vyzerá celkom solídne. Začnime dekódovať: arccos1,8 je uhol, ktorého kosínus sa rovná 1,8... Hop-hop!? 1.8!? Kosínus nemôže byť väčší ako jedna!

Správny. Výraz arccos1,8 nedáva zmysel. A napísanie takéhoto výrazu do nejakej odpovede overovateľa veľmi pobaví.)

Elementárne, ako vidíte.) Každý uhol má svoj vlastný osobný sínus a kosínus. A takmer každý má svoju tangentu a kotangens. Preto, keď poznáte goniometrickú funkciu, môžete zapísať samotný uhol. Na to sú určené arkzíny, arkozíny, arktangens a arkkotangens. Ďalej nazvem celú túto rodinu zdrobneninou - oblúky. písať menej.)

Pozor! Elementárne verbálne a pri vedomí dešifrovanie oblúkov vám umožňuje pokojne a s istotou riešiť rôzne úlohy. A v nezvyčajnéúlohy ukladá len ona.

Je možné prejsť z oblúkov na bežné stupne alebo radiány?- Počujem opatrnú otázku.)

Prečo nie!? ľahko. Môžete ísť tam a späť. Navyše je to niekedy potrebné urobiť. Oblúky sú jednoduchá vec, ale bez nich je to akosi pokojnejšie, však?)

Napríklad: čo je arcsin 0,5?

Pozrime sa na dešifrovanie: arcsin 0,5 je uhol, ktorého sínus je 0,5. Teraz zapnite hlavu (alebo Google) a zapamätajte si, ktorý uhol má sínus 0,5? Sínus je 0,5 r uhol 30 stupňov. To je všetko: arcsin 0,5 je uhol 30°. Pokojne môžete napísať:

arcsin 0,5 = 30°

Alebo, presnejšie, z hľadiska radiánov:

To je všetko, môžete zabudnúť na arcsínus a pracovať ďalej s obvyklými stupňami alebo radiánmi.

Ak ste si uvedomili čo je arcsínus, arkkozín ... Čo je arkustangens, arkustangens ... Potom si ľahko poradíte napríklad s takouto príšerou.)

Neznalý človek zdesene cúvne, áno...) A znalý zapamätajte si dešifrovanie: arcsínus je uhol, ktorého sínus je ... No a tak ďalej. Ak vie aj znalý človek sínusová tabuľka... kosínusová tabuľka. Tabuľka dotyčníc a kotangens, potom nie sú žiadne problémy!

Stačí zvážiť, že:

rozlúštim, t.j. preložte vzorec do slov: uhol, ktorého dotyčnica je 1 (arctg1) je uhol 45°. Alebo, čo je to isté, Pi/4. Podobne:

a to je všetko... Všetky oblúky nahradíme hodnotami v radiánoch, všetko sa zníži, zostáva vypočítať, koľko bude 1 + 1. Bude to 2.) Ktorá je správna odpoveď.

Takto môžete (a mali by ste) prejsť z arcsínusov, arkozínusov, arktangens a arctangens k obyčajným stupňom a radiánom. To výrazne zjednodušuje desivé príklady!

Často sú v takýchto príkladoch vnútri oblúky negatívne hodnoty. Napríklad arctg(-1,3), alebo napríklad arccos(-0,8)... To nie je problém. Tu je niekoľko jednoduchých vzorcov na prechod od negatívneho k pozitívnemu:

Povedzme, že potrebujete určiť hodnotu výrazu:

Môžete to vyriešiť pomocou trigonometrického kruhu, ale nechcete ho kresliť. No dobre. Ide od negatívne hodnoty vo vnútri oblúkového kosínusu na pozitívne podľa druhého vzorca:

Už vo vnútri arkozínu napravo pozitívne význam. Čo

len musíš vedieť. Zostáva nahradiť radiány namiesto kosínusu oblúka a vypočítať odpoveď:

To je všetko.

Obmedzenia týkajúce sa arcsínusu, arkkozínu, arctangensu, arckotangensu.

Je problém s príkladmi 7 - 9? Áno, je tam nejaký trik.)

Všetky tieto príklady, od 1. do 9., sú starostlivo zoradené do políc v § 555.Čo, ako a prečo. So všetkými tajnými pascami a trikmi. Plus spôsoby, ako dramaticky zjednodušiť riešenie. Mimochodom, táto časť obsahuje množstvo užitočných informácií a praktických rád o trigonometrii vo všeobecnosti. A nielen v trigonometrii. Veľa pomáha.

Ak sa vám táto stránka páči...

Mimochodom, mám pre vás niekoľko ďalších zaujímavých stránok.)

Môžete si precvičiť riešenie príkladov a zistiť svoju úroveň. Testovanie s okamžitým overením. Učenie - so záujmom!)

môžete sa zoznámiť s funkciami a deriváciami.

Inverzné goniometrické funkcie(kruhové funkcie, oblúkové funkcie) - matematické funkcie, ktoré sú inverzné k goniometrickým funkciám.

Tieto zvyčajne zahŕňajú 6 funkcií:

• arkzín(symbol: arcsin x; arcsin x je uhol hriechčo sa rovná X),
• arckozín(symbol: arccos x; arccos x je uhol, ktorého kosínus sa rovná X atď),
• oblúková dotyčnica(symbol: arctg x alebo arctan x),
• oblúková dotyčnica(symbol: arcctg x alebo arccot ​​x alebo arccotan x),
• arcsekant(symbol: arcsec x),
• arccosecant(symbol: arccosec x alebo arccsc x).

Arcsine (y = arcsin x) je inverzná funkcia k hriech (x = siny . Inými slovami, vráti uhol o jeho hodnotu hriech.

Oblúkový kosínus (y = arccos x) je inverzná funkcia k cos (x = cos y cos.

Arktangens (y = arktan x) je inverzná funkcia k tg (x = tgy), ktorý má doménu definície a súbor hodnôt . Inými slovami, vráti uhol o jeho hodnotu tg.

Oblúková dotyčnica (y = arcctg x) je inverzná funkcia k ctg (x = ctg y), ktorý má doménu definície a súbor hodnôt. Inými slovami, vráti uhol o jeho hodnotu ctg.

arcsec- arcsekant, vráti uhol o hodnotu jeho secans.

arccosec- arkosekans, vráti uhol o hodnotu svojho kosekansu.

Keď inverzná goniometrická funkcia nie je definovaná v zadanom bode, potom sa jej hodnota vo výslednej tabuľke nezobrazí. Funkcie arcsec a arccosec nie sú definované na segmente (-1,1), ale oblúkový hriech a arccos sú definované len na intervale [-1,1].

Názov inverznej goniometrickej funkcie je vytvorený z názvu zodpovedajúcej goniometrickej funkcie pridaním predpony „ark-“ (z lat. oblúk nás- oblúk). Je to spôsobené tým, že geometricky je hodnota inverznej goniometrickej funkcie spojená s dĺžkou oblúka jednotkovej kružnice (alebo uhlom, ktorý tento oblúk zviera), ktorý zodpovedá jednému alebo druhému segmentu.

Niekedy v zahraničnej literatúre, ako aj vo vedeckých / inžinierskych kalkulačkách, používajú notácie ako hriech −1, cos -1 pre arcsínus, arkozínus a podobne - to sa nepovažuje za úplne presné, pretože pravdepodobná zámena s povýšením funkcie na moc −1 (« −1 » (mínus prvá mocnina) definuje funkciu x=f-1(y), prevrátená funkcia y=f(x)).

Základné vzťahy inverzných goniometrických funkcií.

Tu je dôležité venovať pozornosť intervalom, pre ktoré vzorce platia.

Vzorce týkajúce sa inverzných goniometrických funkcií.

Označte ktorúkoľvek z hodnôt inverzných goniometrických funkcií Arcsin x, Arccos x, Arctan x, Arccot ​​x a ponechajte zápis: arcsin x, arcos x, arctan x, arccot ​​x pre ich hlavné hodnoty, potom vzťah medzi nimi je vyjadrený takýmito vzťahmi.