Points extrêmes d'une fonction en ligne. Extremum d'une fonction de deux variables
À partir de cet article, le lecteur découvrira ce qu'est un extremum de valeur fonctionnelle, ainsi que les caractéristiques de son utilisation dans des activités pratiques. L’étude d’un tel concept est extrêmement importante pour comprendre les fondements des mathématiques supérieures. Ce sujet est fondamental pour une étude plus approfondie du cours.
En contact avec
Qu'est-ce qu'un extremum ?
Dans le cursus scolaire, de nombreuses définitions du concept « extremum » sont données. Cet article est destiné à donner la compréhension la plus profonde et la plus claire du terme à ceux qui ignorent le problème. Ainsi, le terme signifie dans quelle mesure l'écart fonctionnel acquiert un minimum ou valeur maximum sur un plateau ou un autre.
Un extremum est à la fois la valeur minimale et la valeur maximale d’une fonction. Il existe un point minimum et un point maximum, c'est-à-dire les valeurs extrêmes de l'argument sur le graphique. Les principales sciences qui utilisent ce concept sont :
- statistiques;
- contrôle des machines;
- économétrie.
Les points extrêmes jouent un rôle important dans la détermination de la séquence d'une fonction donnée. Le système de coordonnées sur le graphique dans à son meilleur montre le changement de position extrême en fonction du changement de fonctionnalité.
Extrema de la fonction dérivée
Il existe également un phénomène tel que le « dérivé ». Il est nécessaire de déterminer le point extrême. Il est important de ne pas confondre les points minimum ou maximum avec les valeurs les plus élevées et les plus basses. Ce sont des concepts différents, même s’ils peuvent sembler similaires.
La valeur de la fonction est le facteur principal pour déterminer comment trouver le point maximum. La dérivée n'est pas formée de valeurs, mais exclusivement de sa position extrême dans l'un ou l'autre ordre.
La dérivée elle-même est déterminée sur la base de ces points extrêmes, et non sur la valeur la plus grande ou la plus petite. Dans les écoles russes, la frontière entre ces deux concepts n'est pas clairement tracée, ce qui affecte la compréhension de ce sujet en général.
Considérons maintenant un concept tel que « l'extremum aigu ». Aujourd’hui, il existe une valeur minimale aiguë et une valeur maximale aiguë. La définition est donnée conformément à la classification russe des points critiques d'une fonction. Le concept de point extrême est la base pour trouver des points critiques sur un graphique.

Pour définir un tel concept, ils recourent au théorème de Fermat. C'est le plus important dans l'étude des points extrêmes et donne une idée précise de leur existence sous une forme ou une autre. Pour garantir l'extrême, il est important de créer certaines conditions pour une diminution ou une augmentation sur le graphique.
Pour répondre avec précision à la question « comment trouver le point maximum », vous devez suivre ces directives :
- Trouver le domaine exact de définition sur le graphique.
- Rechercher la dérivée d'une fonction et le point extremum.
- Résolvez les inégalités standards pour le domaine où se trouve l’argument.
- Être capable de prouver dans quelles fonctions un point sur un graphique est défini et continu.

Attention! La recherche du point critique d'une fonction n'est possible que s'il existe une dérivée d'au moins du second ordre, ce qui est assuré par une forte proportion de présence d'un point extremum.
Condition nécessaire à l'extremum d'une fonction
Pour qu’un extremum existe, il est important qu’il y ait à la fois un minimum et un maximum de points. Si cette règle n'est que partiellement respectée, alors la condition d'existence d'un extremum est violée.

Chaque fonction, quelle que soit sa position, doit être différenciée afin d'identifier ses nouvelles significations. Il est important de comprendre que le cas où un point tend vers zéro n’est pas le principe principal pour trouver un point dérivable.
Un extremum aigu, ainsi qu'un minimum d'une fonction, sont un aspect extrêmement important de la résolution d'un problème mathématique utilisant des valeurs extrêmes. Afin de mieux comprendre ce composant, il est important de se référer aux valeurs tabulaires pour spécifier la fonctionnalité.
| Recherche pleine de sens | Tracer un graphique de valeurs |
| 1. Détermination des points de valeurs croissantes et décroissantes. 2. Recherche de points de discontinuité, d'extremum et d'intersection avec des axes de coordonnées. 3. Le processus de détermination des changements de position sur un graphique. 4. Détermination de l'indicateur et de la direction de convexité et de convexité, en tenant compte de la présence d'asymptotes. 5. Création d'un tableau récapitulatif de recherche du point de vue de la détermination de ses coordonnées. 6. Trouver les intervalles de points extrêmes et pointus croissants et décroissants. 7. Détermination de la convexité et de la concavité d'une courbe. 8. Tracer un graphique prenant en compte la recherche permet de trouver le minimum ou le maximum. |
L'élément principal lorsqu'il est nécessaire de travailler avec des points extrêmes est la construction précise de son graphique. Les enseignants des écoles n'accordent pas souvent la plus grande attention à un aspect aussi important, ce qui constitue une violation flagrante du processus éducatif. La construction d'un graphique se produit uniquement sur la base des résultats de l'étude des données fonctionnelles, de l'identification des extrema aigus, ainsi que des points sur le graphique. Les extrema nets de la fonction dérivée sont affichés sur un tracé de valeurs exactes, en utilisant procédure standard détermination des asymptotes. Les points maximum et minimum de la fonction sont accompagnés de plus constructions complexes arts graphiques. Cela est dû à un besoin plus profond de résoudre le problème de l’extremum aigu. Il faut aussi trouver la dérivée d’une fonction complexe et simple, puisque c’est l’un des concepts les plus importants du problème de l’extremum. |
Extremum du fonctionnel
Afin de trouver la valeur ci-dessus, vous devez respecter les règles suivantes :
- déterminer la condition nécessaire pour une relation extrême ;
- prendre en compte l'état suffisant des points extrêmes du graphique ;
- effectuer le calcul de l'extremum aigu.
Des concepts tels que minimum faible et minimum fort sont également utilisés. Ceci doit être pris en compte lors de la détermination de l'extremum et de son calcul précis. Dans le même temps, la fonctionnalité aiguë est la recherche et la création de toutes les conditions nécessaires pour travailler avec le graphique d'une fonction.
Définition 1. Le point M(x 0 ; y 0) est appelé point maximum (minimum) de la fonction z = f(x; y) s'il existe un voisinage du point M tel que pour tous les points (x; y) de ce quartier, l’inégalité suivante est vraie :
f(x 0 ; y 0) f(x; y), .
Théorème 1
(une condition nécessaire à l'existence d'un extremum)
. Si une fonction différentiable z = f(x; y) atteint un extremum au point M(x 0 ; y 0), alors ses dérivées partielles du premier ordre en ce point sont égales à zéro, c'est-à-dire  ;
;
Les points auxquels les dérivées partielles sont égales à zéro sont appelés Stationnaire ou points critiques.
Théorème 2 (condition suffisante pour l'existence d'un extremum)
Soit la fonction z = f(x; y) :
a) défini dans un certain voisinage du point (x 0 ; y 0), dans lequel  Et
Et  ;
;
b) a des dérivées partielles continues du deuxième ordre à ce stade
 ;
;


Alors, si = AC B 2 > 0, alors au point (x 0 ; y 0) la fonction z = f(x; y) a un extremum, et si A< 0 (или С < 0) – максимум, если А >0 (ou C > 0) – minimum. Dans le cas = AC B 2< 0, функция z = f(x; y) экстремума не имеет. Если = AC B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).
Exemple 1. Trouver l'extremum de la fonction z = x 2 + xy + y 2 3x 6y.
Solution. Trouvons les dérivées partielles du premier ordre :


Utilisons la condition nécessaire à l'existence d'un extremum :


En résolvant le système d'équations, on trouve les coordonnées x et y des points stationnaires : x = 0 ; y = 3, c'est-à-dire M(0; 3).
Calculons les dérivées partielles du second ordre et trouvons leurs valeurs au point M.
UNE =  = 2 ; C =
= 2 ; C =  = 2;
= 2;
B =  .
.
Composons le discriminant = AC B 2 = 2 2 1 > 0, A = 2 > 0. Par conséquent, au point M(0 ; 3) la fonction donnée a un minimum. La valeur de la fonction à ce stade est z min = 9.
Trouver les extrema des fonctions
322. z = x 2 + y 2 + xy 4x 5y 323. z = y 3 x 3 3xy
324. z = x 2 2xy + 4y 3 325. z =  y 2 x + 6 ans
y 2 x + 6 ans
326. z = x y (1 x y) 327. z = 2xy 4x 2y
328. z = e x/2 (x + y 2) 329. z = x 3 + 8y 3 6xy + 1
330. z = 3x 2 y x 3 y 4 331. z = 3x + 6y x 2 xy + y 2
Les valeurs les plus grandes et les plus petites d'une fonction de deux variables dans un domaine fermé
Pour trouver le plus grand Et moins valeurs d'une fonction dans une région fermée, il faut :
1) trouver les points critiques situés dans une zone donnée et calculer les valeurs de fonction en ces points ;
2) trouver les points critiques à la limite de la région et calculer les valeurs les plus grandes et les plus petites des fonctions qui y sont associées ;
3) parmi toutes les valeurs trouvées, sélectionnez la plus grande et la plus petite.
Exemple 2. Trouver les valeurs les plus grandes et les plus petites de la fonction z =  dans un cercle x 2 + y 2 1.
dans un cercle x 2 + y 2 1.
Solution. Trouvons les coordonnées des points critiques situés à l'intérieur de la région considérée, pour lesquelles nous calculons les dérivées partielles du premier ordre de la fonction z et les assimilons à zéro.




d'où x = 0, y = 0 et, donc, M(0; 0) est un point critique.
Calculons la valeur de la fonction z au point M(0; 0) : z(0; 0) = 2.
Trouvons les points critiques sur la limite de la région - un cercle défini par l'équation x 2 + y 2 = 1. En remplaçant y 2 = 1 - x 2 dans la fonction z = z(x; y), nous obtenons une fonction d'une variable
z =  ;
;
où x[1; 1].
Après avoir calculé la dérivée  et en l'assimilant à zéro, nous obtenons des points critiques sur la limite de la région x 1 = 0, x 2 =
et en l'assimilant à zéro, nous obtenons des points critiques sur la limite de la région x 1 = 0, x 2 =  , x 3 =
, x 3 = 
Trouvons la valeur de la fonction z(x) =  aux points critiques et aux extrémités du segment [1 ; 1] : z(0) = ;
aux points critiques et aux extrémités du segment [1 ; 1] : z(0) = ;  =;
=; ; z(1) = ; z(1) =
; z(1) = ; z(1) = 
Choisissons la plus grande et la plus petite parmi les valeurs de la fonction z aux points critiques situés à l'intérieur et sur la limite du cercle.
Donc z max. = z(0; 0) = 2
Dans les problèmes d'optimisation, il est nécessaire de trouver des extrema fonctions de deux variables ou plusà condition qu'il existe une relation entre les variables de cette relation, donnée par l'équation ![]() . Dans ce cas, nous disons qu'il faut trouver conditionnel extrême
.
. Dans ce cas, nous disons qu'il faut trouver conditionnel extrême
.
Afin de trouver l'extremum conditionnel, vous devez trouver dérivées partielles et décider systèmes d'équations Il existe un algorithme pour trouver un extremum conditionnel en trois étapes, que nous allons maintenant analyser à l'aide d'un exemple, et la signification géométrique d'un extremum conditionnel, qui devrait atteindre tout le monde lors de l'analyse de cet exemple même.
Nous analyserons donc l'algorithme en utilisant l'exemple du problème le plus courant : trouver l'extremum conditionnel d'une fonction de deux variables. .
Étape 1. Introduit Fonction de Lagrange
où le premier terme est la fonction d'origine elle-même et le deuxième terme avec un signe moins est le côté gauche de l'équation de la condition de connexion, multiplié par (lambda) - le multiplicateur de Lagrange.
Exemple 1. Trouver conditions extrêmes une fonction de deux variables exprimant l'aire d'un rectangle en fonction de ses côtés X Et ouià condition qu'il y ait une corde qui puisse délimiter ce rectangle, et que la longueur de cette corde soit de 100.
Étape 1. Solution. Amenons l'équation de la condition de connexion à la forme requise avec zéro à droite :
![]() .
.
Composons Fonction de Lagrange:
Étape 2. Nous composons un système d'équations à partir d'égalités dérivées partielles zéro et l'équation de la condition de connexion (signe nécessaire de l'existence d'un extremum conditionnel) :
Les solutions de ce système d'équations sont des points d'un éventuel extremum conditionnel - des points stationnaires ou, comme on dit aussi, des points critiques.
Exemple 1. Étape 2.
Solution.

X Et oui :
Remplaçons ces expressions dans la troisième équation et trouvons la valeur du multiplicateur de Lagrange :

X Et oui et retrouvez les valeurs des variables de la fonction d'origine :

Nous avons reçu et. Ces valeurs sont aussi les coordonnées du point stationnaire. Ainsi, nous avons obtenu un point stationnaire.
Étape 3. Soit le point stationnaire trouvé à l'étape 2. Pour déterminer si l'extremum conditionnel est un minimum ou un maximum, vous devez trouver la deuxième différentielle de la fonction de Lagrange
![]()
et dans l'expression résultante, remplacez à la place de « lambda » ses valeurs (les valeurs du multiplicateur de Lagrange) trouvées à l'étape 2.
Si la valeur de la deuxième différentielle de la fonction de Lagrange est inférieure à zéro (), alors le point stationnaire est un point maximum ; si elle est supérieure à zéro (), alors le point stationnaire est un point minimum. Si la valeur de la deuxième différentielle de la fonction de Lagrange est égale à zéro, des recherches supplémentaires sont nécessaires, mais de tels cas ne se retrouvent pratiquement pas dans les problèmes assignés aux étudiants.
Les coordonnées des points fixes sont substituées au point de départ et, ainsi, nous trouvons finalement conditions extrêmes (ou minimum et maximum ou l'un de ces extrêmes).
Exemple 1. Étape 3.
Solution. Trouvons la deuxième différentielle de la fonction de Lagrange :
![]()
Dans notre cas, puisque les première et troisième composantes sont égales à zéro, nous n'avons pas besoin d'y substituer les valeurs du multiplicateur de Lagrange. Mais il faut trouver la relation entre les différentiels dx Et mourir :
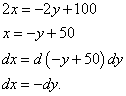
Puisque les valeurs obtenues sont de signe opposé, on constate que dans tous les cas .
Maintenant nous pouvons trouver la valeur conditionnel extrême de la fonction originale, qui est le maximum :
![]() .
.
Il s'agit de la surface maximale d'un rectangle spécifié par la fonction d'origine, qui peut être limitée par une corde dont la longueur est de 100.
Exemple 2. Trouver conditions extrêmes
Étape 1. Composons Fonction de Lagrange:
Étape 2. Trouvons les dérivées partielles de la fonction de Lagrange et composons un système d'équations à partir de leurs égalités à zéro et l'équation de la condition de connexion :

A partir des première et deuxième équations, nous exprimons respectivement X Et oui :

Remplaçons ces expressions dans la troisième équation et trouvons les valeurs du multiplicateur de Lagrange :

Remplaçons maintenant la valeur du multiplicateur de Lagrange dans les expressions pour X Et oui et retrouver les valeurs des variables de la fonction d'origine pour deux valeurs du multiplicateur de Lagrange :

Ces valeurs x et y sont les coordonnées de deux points stationnaires. On obtient ainsi des points stationnaires ![]() .
.
Étape 3. Trouvons les dérivées partielles du second ordre de la fonction de Lagrange :
Trouvons la deuxième différentielle de la fonction de Lagrange en utilisant la formule
![]() :
:
![]()
Nous avons reçu une valeur inférieure à zéro, donc point - point maximum conditionnel:
![]() .
.
Établissons le signe de la différentielle seconde de la fonction de Lagrange à la valeur du multiplicateur de Lagrange :
![]()
Nous avons reçu une valeur supérieure à zéro, donc point - point minimum conditionnel:
![]() .
.
Ainsi, conditions extrêmes les fonctions données sont trouvées.
Exemple 3. Trouver conditions extrêmes fonctions de deux variables soumises à .
Étape 1. Composons Fonction de Lagrange:
Étape 2. Trouvons les dérivées partielles de la fonction de Lagrange et composons un système d'équations à partir de leurs égalités à zéro et l'équation de la condition de connexion :

A partir des première et deuxième équations, nous exprimons respectivement X Et oui :

Nous constatons cependant que la substitution de ces valeurs variables dans la troisième équation du système ne donne pas l'égalité correcte. Nous pensons donc qu'en fait le deuxième facteur de l'égalité est égal à zéro : . De là, nous obtenons
On recherche les coordonnées de points stationnaires à la valeur du multiplicateur de Lagrange. Ensuite, d’après les expressions pour X et Y du système d’équations, il s’ensuit que . De la troisième équation du système nous obtenons.
Un concept important en mathématiques est la fonction. Avec son aide, vous pouvez représenter visuellement de nombreux processus se produisant dans la nature et refléter la relation entre certaines quantités à l'aide de formules, de tableaux et d'images sur un graphique. Un exemple est la dépendance de la pression d'une couche de liquide sur un corps à la profondeur d'immersion, l'accélération à l'action d'une certaine force sur un objet, une augmentation de la température à l'énergie transférée et bien d'autres processus. Étudier une fonction implique de construire un graphique, de connaître ses propriétés, son domaine de définition et ses valeurs, ses intervalles d'augmentation et de diminution. Un point important dans ce processus est de trouver des points extrêmes. Nous parlerons plus loin de la façon de procéder correctement.
À propos du concept lui-même à l'aide d'un exemple précis
En médecine, tracer un graphique fonctionnel peut nous renseigner sur l’évolution d’une maladie dans le corps d’un patient, reflétant clairement son état. Supposons que l'axe OX représente le temps en jours et que l'axe OU représente la température du corps humain. La figure montre clairement comment cet indicateur augmente fortement puis diminue. Il est également facile de remarquer des points particuliers reflétant les moments où une fonction, auparavant croissante, commence à diminuer, et vice versa. Ce sont des points extrêmes, c’est-à-dire des valeurs critiques (maximales et minimales) dans ce cas de la température du patient, après quoi des changements dans son état se produisent.

Angle d'inclinaison
Vous pouvez facilement déterminer à partir de la figure comment la dérivée de la fonction change. Si les droites du graphique augmentent avec le temps, alors c’est positif. Et plus ils sont raides, plus la valeur de la dérivée est grande, à mesure que l'angle d'inclinaison augmente. Pendant les périodes de diminution, cette valeur prend des valeurs négatives, se tournant vers zéro aux points extrêmes, et le graphique de la dérivée dans ce dernier cas est tracé parallèlement à l'axe OX.
Tout autre processus doit être traité de la même manière. Mais la meilleure façon de comprendre ce concept est le mouvement des différents corps, clairement indiqué dans les graphiques.
Mouvement
Supposons qu’un objet se déplace en ligne droite, prenant uniformément de la vitesse. Pendant cette période, le changement des coordonnées du corps est représenté graphiquement par une certaine courbe, qu'un mathématicien appellerait une branche de parabole. Dans le même temps, la fonction augmente constamment, car les indicateurs de coordonnées changent de plus en plus vite chaque seconde. Le graphique de vitesse montre le comportement de la dérivée dont la valeur augmente également. Cela signifie que le mouvement ne présente aucun point critique.
Cela continuerait indéfiniment. Mais que se passe-t-il si le corps décide soudainement de ralentir, de s’arrêter et de commencer à bouger dans une direction différente ? Dans ce cas, les indicateurs de coordonnées commenceront à diminuer. Et la fonction dépassera une valeur critique et passera de l'augmentation à la diminution.

A l'aide de cet exemple, on peut encore comprendre que des points extrêmes sur le graphique d'une fonction apparaissent aux moments où elle cesse d'être monotone.
Signification physique du dérivé
Ce qui a été décrit précédemment a clairement montré que la dérivée est essentiellement le taux de changement de la fonction. Cette précision contient son signification physique. Les points extrêmes sont des zones critiques sur le graphique. Ils peuvent être identifiés et détectés en calculant la valeur de la dérivée, qui s'avère égale à zéro.
Il existe un autre signe qui constitue une condition suffisante pour un extremum. La dérivée à de tels points d'inflexion change de signe : de « + » à « - » dans la zone maximale et de « - » à « + » dans la zone minimale.

Mouvement sous l'influence de la gravité
Imaginons une autre situation. Les enfants, jouant avec un ballon, le lançaient de telle manière qu'il commençait à se déplacer en biais par rapport à l'horizon. Au moment initial, la vitesse de cet objet était la plus élevée, mais sous l'influence de la gravité, elle a commencé à diminuer, et à chaque seconde d'une valeur égale à environ 9,8 m/s 2 . C'est la valeur de l'accélération qui se produit sous l'influence de la gravité terrestre lors d'une chute libre. Sur la Lune, elle serait environ six fois plus petite.
Le graphique décrivant le mouvement d’un corps est une parabole dont les branches pointent vers le bas. Comment trouver les points extrêmes ? Dans ce cas, il s'agit du sommet de la fonction, où la vitesse du corps (balle) prend la valeur nulle. La dérivée de la fonction devient nulle. Dans ce cas, la direction, et donc la valeur de la vitesse, change dans le sens inverse. Le corps descend plus vite chaque seconde et accélère de la même manière - 9,8 m/s 2 .

Dérivée seconde
Dans le cas précédent, le graphique du module de vitesse est tracé sous forme de ligne droite. Cette ligne est initialement dirigée vers le bas, puisque la valeur de cette valeur diminue constamment. Ayant atteint zéro à un moment donné, les indicateurs de cette valeur commencent à augmenter et la direction de la représentation graphique du module de vitesse change radicalement. La ligne pointe désormais vers le haut.
La vitesse, étant une dérivée de la coordonnée par rapport au temps, présente également un point critique. Dans cette région, la fonction, initialement décroissante, commence à augmenter. C'est l'emplacement du point extremum de la dérivée de la fonction. Dans ce cas, l'angle d'inclinaison de la tangente devient nul. Et l'accélération, étant la dérivée seconde de la coordonnée par rapport au temps, change de signe de « - » à « + ». Et le mouvement d’uniformément lent devient uniformément accéléré.
Graphique d'accélération
Regardons maintenant quatre images. Chacun d'eux affiche un graphique des changements dans le temps d'une quantité physique telle que l'accélération. Dans le cas de « A », sa valeur reste positive et constante. Cela signifie que la vitesse du corps, tout comme ses coordonnées, augmente constamment. Si l'on imagine que l'objet se déplacera ainsi pendant un temps infiniment long, la fonction reflétant la dépendance de la coordonnée au temps s'avérera constamment croissante. Il s'ensuit qu'il ne comporte pas de zones critiques. Il n'y a pas non plus de points extrêmes sur le graphique de la dérivée, c'est-à-dire une vitesse variant linéairement.

Il en va de même pour le cas « B » avec une accélération positive et en constante augmentation. Certes, les graphiques des coordonnées et de la vitesse seront ici un peu plus compliqués.
Quand l'accélération devient nulle
En regardant la figure « B », on peut observer une image complètement différente caractérisant le mouvement du corps. Sa vitesse sera représentée graphiquement par une parabole aux branches dirigées vers le bas. Si l'on continue la ligne décrivant le changement d'accélération jusqu'à son intersection avec l'axe OX et plus loin, on peut imaginer que jusqu'à cette valeur critique, où l'accélération s'avère nulle, la vitesse de l'objet augmentera de plus en plus lentement . Le point extrême de la dérivée de la fonction de coordonnées sera exactement au sommet de la parabole, après quoi le corps changera radicalement la nature de son mouvement et commencera à se déplacer dans une direction différente.
Dans le dernier cas, « G », la nature du mouvement ne peut être déterminée avec précision. Ici, nous savons seulement qu'il n'y a pas d'accélération pendant une certaine période considérée. Cela signifie que l’objet peut rester en place ou se déplacer à une vitesse constante.
Problème d'addition de coordonnées
Passons aux tâches souvent rencontrées lors de l'étude de l'algèbre à l'école et proposées pour la préparation à l'examen d'État unifié. La figure ci-dessous montre le graphique de la fonction. Il est nécessaire de calculer la somme des points extremum.

Faisons cela pour l'axe des ordonnées en déterminant les coordonnées des zones critiques où un changement dans les caractéristiques de la fonction est observé. En termes simples, nous trouverons les valeurs le long de l'axe OX pour les points d'inflexion, puis procéderons à l'addition des termes résultants. D'après le graphique, il est évident qu'ils prennent les valeurs suivantes : -8 ; -7 ; -5 ; -3 ; -2 ; 1; 3. Cela donne -21, ce qui est la réponse.
Solution optimale
Il n'est pas nécessaire d'expliquer à quel point il peut être important de mettre en œuvre tâches pratiques choisir la solution optimale. Après tout, il existe de nombreuses façons d'atteindre un objectif, mais la meilleure solution, en règle générale, n'en est qu'une. Cela est extrêmement nécessaire, par exemple, lors de la conception de navires, de vaisseaux spatiaux et d'avions, ainsi que de structures architecturales, pour trouver la forme optimale de ces objets fabriqués par l'homme.

La vitesse des véhicules dépend en grande partie de la minimisation appropriée de la résistance qu'ils subissent lorsqu'ils se déplacent dans l'eau et l'air, des surcharges qui surviennent sous l'influence des forces gravitationnelles et de nombreux autres indicateurs. Un navire en mer requiert des qualités telles que la stabilité lors d'une tempête ; pour un navire fluvial, un tirant d'eau minimum est important. Lors du calcul de la conception optimale, les points extrêmes sur le graphique peuvent clairement donner une idée de la meilleure solution problème complexe. Les problèmes de ce type sont souvent résolus en économie, dans les domaines commerciaux et dans de nombreuses autres situations de la vie.
De l'histoire ancienne
Même les anciens sages étaient préoccupés par des problèmes extrêmes. Les scientifiques grecs ont réussi à percer le mystère des zones et des volumes grâce à des calculs mathématiques. Ils furent les premiers à comprendre que sur un plan composé de différentes figures ayant le même périmètre, le cercle a toujours la plus grande surface. De même, la balle est dotée du volume maximum parmi les autres objets de l'espace ayant la même surface. Des personnalités aussi célèbres qu'Archimède, Euclide, Aristote et Apollonius se sont consacrées à résoudre ces problèmes. Heron était excellent pour trouver les points extrêmes et, à l'aide de calculs, il construisait des dispositifs ingénieux. Il s'agissait notamment de machines se déplaçant à vapeur, de pompes et de turbines fonctionnant sur le même principe.

Construction de Carthage
Il existe une légende dont l'intrigue est basée sur la résolution de l'un des problèmes extrêmes. Le résultat de l'approche commerciale démontrée par la princesse phénicienne, qui s'est tournée vers les sages pour obtenir de l'aide, fut la construction de Carthage. Le terrain de cette ville ancienne et célèbre a été donné à Didon (c'était le nom du souverain) par le chef d'une des tribus africaines. La superficie du lotissement ne lui paraissait pas très grande au début, puisque selon le contrat elle était censée être recouverte de peau de bœuf. Mais la princesse ordonna à ses soldats de le couper en fines lanières et d'en faire une ceinture. Il s’est avéré si long qu’il couvrait une zone pouvant accueillir une ville entière.
Origines de l'analyse mathématique
Passons maintenant des temps anciens à une époque ultérieure. Il est intéressant de noter que Kepler a été incité à comprendre les fondements de l’analyse mathématique au XVIIe siècle lors d’une rencontre avec un vendeur de vin. Le marchand était si compétent dans son métier qu'il pouvait facilement déterminer le volume de la boisson dans le tonneau simplement en y abaissant une corde de fer. En réfléchissant à une telle curiosité, le célèbre scientifique a réussi à résoudre lui-même ce dilemme. Il s'avère que d'habiles tonneliers de l'époque avaient l'habitude de fabriquer des récipients de telle manière qu'à une certaine hauteur et un certain rayon de circonférence des anneaux de fixation, ils avaient une capacité maximale.
Cela est devenu une raison pour Kepler de réfléchir plus avant. Les tonneliers sont parvenus à la solution optimale grâce à de longues recherches, des erreurs et de nouvelles tentatives, transmettant leur expérience de génération en génération. Mais Kepler voulait accélérer le processus et apprendre à faire la même chose en peu de temps grâce à des calculs mathématiques. Tous ses développements, repris par ses collègues, se sont transformés en les désormais célèbres théorèmes de Fermat et de Newton-Leibniz.
Problème de surface maximale
Imaginons que nous ayons un fil dont la longueur est de 50 cm, comment pouvons-nous en faire un rectangle ayant la plus grande surface ?
Lorsque vous prenez une décision, vous devez partir de vérités simples connues de tous. Il est clair que le périmètre de notre figure sera de 50 cm et qu'il est composé du double de la longueur des deux côtés. Cela signifie qu'après avoir désigné l'un d'eux par « X », l'autre peut être exprimé par (25 - X).
De là, nous obtenons une aire égale à X(25 - X). Cette expression peut être considérée comme une fonction qui prend plusieurs valeurs. Pour résoudre le problème, il faut en trouver le maximum, ce qui signifie que vous devez connaître les points extrêmes.
Pour ce faire, nous trouvons la dérivée première et l'assimilons à zéro. Le résultat est une équation simple : 25 - 2X = 0.
Nous en apprenons que l'un des côtés est X = 12,5.
Donc l'autre : 25 - 12,5 = 12,5.
Il s'avère que la solution au problème sera un carré de 12,5 cm de côté.

Comment trouver la vitesse maximale
Regardons un autre exemple. Imaginons qu'il y ait un corps, mouvement rectiligne qui est décrite par l'équation S = - t 3 + 9t 2 - 24t - 8, où la distance parcourue est exprimée en mètres et le temps en secondes. Nous devons trouver la vitesse maximale. Comment faire? Téléchargé, on retrouve la vitesse, c'est-à-dire la dérivée première.
Nous obtenons l'équation : V = - 3t 2 + 18t - 24. Maintenant, pour résoudre le problème, nous devons à nouveau trouver les points extremum. Cela doit être fait de la même manière que dans la tâche précédente. Nous trouvons la dérivée première de la vitesse et l'assimilons à zéro.
On obtient : - 6t + 18 = 0. Donc t = 3 s. C’est le moment où la vitesse du corps prend une valeur critique. Nous substituons les données résultantes dans l'équation de vitesse et obtenons : V = 3 m/s.
Mais comment comprendre ce que c'est ? vitesse maximum, parce que les points critiques d'une fonction peuvent être ses valeurs les plus grandes ou les plus petites ? Pour vérifier, vous devez trouver la dérivée seconde de la vitesse. Il est exprimé par le chiffre 6 avec un signe moins. Cela signifie que le point trouvé est un maximum. Et au cas où valeur positive la dérivée seconde serait un minimum. Cela signifie que la solution trouvée s'est avérée correcte.
Les problèmes donnés en exemple ne sont qu'une partie de ceux qui peuvent être résolus si l'on sait trouver les points extremum d'une fonction. En fait, il y en a beaucoup plus. Et une telle connaissance ouvre des possibilités illimitées à la civilisation humaine.
Fonction y = f(x) est appelé en augmentant (décroissant) dans un certain intervalle, si pour x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).
Si la fonction différentiable y = f (x) augmente (diminue) sur un intervalle, alors sa dérivée sur cet intervalle f " (X)> 0
(F"(X)< 0).
Point X Ô appelé point maximum local (le minimum) fonction f (x) s'il existe un voisinage du point xo, pour tous les points dont l'inégalité f (x) est vraie≤ f (x o ) (f (x )≥ f (x o )).
Les points maximum et minimum sont appelés points extrêmes, et les valeurs de la fonction en ces points sont ses extrêmes.
Points extrêmes
Les conditions nécessaires extrême . Si le point X Ô est le point extremum de la fonction f(x), alors soit f " (x o ) = 0, ou f(x o ) n’existe pas. De tels points sont appelés critique, et la fonction elle-même est définie au point critique. Parmi ses points critiques, il faut chercher les extrema d’une fonction.
La première condition suffisante. Laisser X Ô - point critique. Si f" (x ) lors du passage par un point X Ô change le signe plus en moins, puis au point xo la fonction a un maximum, sinon elle a un minimum. Si, en passant par le point critique, la dérivée ne change pas de signe, alors au point X Ô il n'y a pas d'extrême.
Deuxième condition suffisante.
Soit la fonction f(x)
F" (x ) à proximité du point X
Ô
et la dérivée seconde f "" (x 0) au point lui-même xo. Si f"(xo) = 0, f "" (x 0)>0 (f "" (x 0)<0), то точка xo est le point minimum (maximum) local de la fonction f (x). Si f "" (x 0) = 0, alors vous devez soit utiliser la première condition suffisante, soit impliquer des conditions plus élevées.
Sur un segment, la fonction y = f (x) peut atteindre sa valeur minimale ou maximale soit aux points critiques, soit aux extrémités du segment.
Exemple 3.22.
Solution. Parce que F " (
Problèmes de recherche de l'extremum d'une fonction
Exemple 3.23. un
Solution. X Et oui oui
0
≤ X≤
> 0, et quand x >a /4S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
les fonctions kv.
unités).
Exemple 3.24. p ≈
Solution. p p
S"
R = 2, H = 16/4 = 4.
Exemple 3.22.Trouvez les extrema de la fonction f (x) = 2x 3 - 15x 2 + 36x - 14.
Solution. Parce que F " (x ) = 6x 2 - 30x +36 = 6(x -2)(x - 3), alors les points critiques de la fonction x 1 = 2 et x 2 = 3. Les extrema ne peuvent être qu'à ces points. Puisque en passant par le point x 1 = 2 la dérivée change de signe de plus à moins, alors à ce stade la fonction a un maximum. En passant par le point x 2 = 3, la dérivée change de signe de moins à plus, donc au point x 2 = 3 la fonction a un minimum. Après avoir calculé les valeurs de fonction aux points
x 1 = 2 et x 2 = 3, on retrouve les extrema de la fonction : maximum f (2) = 14 et minimum f (3) = 13.
Exemple 3.23.Il est nécessaire de construire une zone rectangulaire près du mur de pierre de manière à ce qu'elle soit clôturée sur trois côtés avec un treillis métallique et que le quatrième côté soit adjacent au mur. Pour cela il y a un mètres linéaires de maille. À quel rapport hauteur/largeur le site aura-t-il la plus grande superficie ?
Solution.Désignons les côtés de la plate-forme par X Et oui. La superficie du site est S = xy. Laisser oui- c'est la longueur du côté adjacent au mur. Alors, par condition, l'égalité 2x + y = a doit être satisfaite. Donc y = a - 2x et S = x (a - 2x), où
0
≤ X≤ a /2 (la longueur et la largeur de la zone ne peuvent pas être négatives). S " = a - 4x, a - 4x = 0 à x = a/4, d'où
y = une - 2 × une/4 = une/2. Parce que le x = a /4 est le seul point critique ; vérifions si le signe de la dérivée change en passant par ce point. À x a /4 S "> 0, et quand x >a /4S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
les fonctions S(une/4) = une/4(une - une/2) = une 2 /8 (kv.
unités).
Puisque S est continu et que ses valeurs aux extrémités S(0) et S(a /2) sont égales à zéro, alors la valeur trouvée sera la plus grande valeur de la fonction. Ainsi, le rapport hauteur/largeur le plus favorable du site dans les conditions données du problème est y = 2x.
Exemple 3.24.Il est nécessaire de fabriquer un réservoir cylindrique fermé d'une capacité de V=16 p ≈ 50 m3. Quelles doivent être les dimensions du réservoir (rayon R et hauteur H) pour que le moins de matière soit utilisé pour sa fabrication ?
Solution.La surface totale du cylindre est S = 2 p R(R+H). On connaît le volume du cylindre V = p R 2 Н Þ Н = V/ p R 2 =16 p / p R2 = 16/R2. Donc S(R) = 2 p (R2 +16/R). On retrouve la dérivée de cette fonction :
S"(R) = 2 p (2R- 16/R 2) = 4 p (R- 8/R 2). S" (R) = 0 à R 3 = 8, donc,
R = 2, H = 16/4 = 4.



