Državna proračunska obrazovna ustanova

Srednje opće obrazovanje regije Samara

Škola br. 2 nazvana po. V. Maskina željeznica Umjetnost. Klyavlino

Općinski okrug Klyavlinsky

regija Samara

« Jednadžbe

I

nejednakosti

s parametrima"

tutorial

Klyavlino

Tutorial

"Jednadžbe i nejednadžbe s parametrima" za učenike od 10. do 11. razreda

ovaj priručnik je dodatak programu izbornog kolegija "Jednadžbe i nejednadžbe s parametrima", koji je prošao vanjski ispit (znanstveni i metodološki stručni savjet Ministarstva obrazovanja i znanosti Samarske regije od 19. prosinca 2008. preporučio je za korištenje u obrazovnim ustanovama regije Samara)

Autori

Romadanova Irina Vladimirovna

profesorica matematike u Srednjoškolskoj ustanovi Klyavlinskaya

Škola br. 2 nazvana po. V. Maskina, okrug Klyavlinsky, regija Samara

Serbajeva Irina Aleksejevna

Uvod………………………………………………………………3-4

Linearne jednadžbe i nejednadžbe s parametrima……………..4-7

Kvadratne jednadžbe i nejednadžbe s parametrima……………7-9

Frakcijsko-racionalne jednadžbe s parametrima……………..10-11

Iracionalne jednadžbe i nejednadžbe s parametrima……11-13

Trigonometrijske jednadžbe i nejednadžbe s parametrima.14-15

Eksponencijalne jednadžbe i nejednadžbe s parametrima………16-17

Logaritamske jednadžbe i nejednadžbe s parametrima......16-18

Ciljevi jedinstvenog državnog ispita…………………………………………………………...18-20

Zadaci za samostalan rad……………………………21-28

Uvod.

Jednadžbe i nejednadžbe s parametrima.

Ako u jednadžbi ili nejednadžbi neki koeficijenti nemaju određene brojčane vrijednosti, već su označeni slovima, tada se nazivaju parametri, i sama jednadžba ili nejednadžba parametarski.

Da biste riješili jednadžbu ili nejednadžbu s parametrima potrebno je:

Izaberi posebno značenje- ovo je vrijednost parametra u kojem ili pri prolasku kroz koji se mijenja rješenje jednadžbe ili nejednadžbe.

Definirati važeće vrijednosti– to su vrijednosti parametra pri kojima jednadžba ili nejednadžba ima smisla.

Rješavanje jednadžbe ili nejednadžbe s parametrima znači:

1) odrediti pri kojim vrijednostima parametara postoje rješenja;

2) za svaki dopustivi sustav vrijednosti parametara pronaći odgovarajući skup rješenja.

Jednadžbu s parametrom možete riješiti pomoću sljedećih metoda: analitičke ili grafičke.

Analitička metoda uključuje zadatak proučavanja jednadžbe razmatranjem nekoliko slučajeva, od kojih se nijedan ne može propustiti.

Rješavanje jednadžbi i nejednadžbi s parametrima svake vrste analitičkom metodom uključuje detaljnu analizu situacije i dosljedno istraživanje, tijekom kojeg se javlja potreba "pažljivo rukovanje" s parametrom.

Grafička metoda uključuje konstruiranje grafa jednadžbe iz kojeg se može odrediti kako promjena parametra utječe na rješenje jednadžbe. Graf vam ponekad omogućuje da analitički formulirate potrebne i dovoljne uvjete za rješavanje problema. Metoda grafičkog rješenja posebno je učinkovita kada trebate utvrditi koliko korijena jednadžba ima ovisno o parametru i ima nedvojbenu prednost što to jasno vidite.

§ 1. Linearne jednadžbe i nejednadžbe.

Linearna jednadžba A x = b , napisano u općem obliku, može se smatrati jednadžbom s parametrima, gdje x – nepoznato , a , b - opcije. Za ovu jednadžbu, posebna ili kontrolna vrijednost parametra je ona kod koje koeficijent nepoznanice postaje nula.

Pri rješavanju linearne jednadžbe s parametrom razmatraju se slučajevi kada je parametar jednak svojoj posebnoj vrijednosti, a različit od nje.

Posebna vrijednost parametra a je vrijednost A = 0.

b = 0 je posebna vrijednost parametra b .

Na b ¹ 0 jednadžba nema rješenja.

Na b = 0 jednadžba će imati oblik: 0x = 0. Rješenje ove jednadžbe je bilo koji realni broj.

Nejednakosti oblika ah > b I sjekira < b (a ≠ 0) nazivaju se linearne nejednadžbe. Skup rješenja nejednakosti ah >b– interval

(; +), Ako a > 0 , I (-;) , Ako A< 0 . Slično za nejednakost

Oh< b skup rješenja – interval(-;), Ako a > 0, I (; +), Ako A< 0.

Primjer 1. Riješite jednadžbu sjekira = 5

Riješenje: Ovo je linearna jednadžba.

Ako a = 0, zatim jednadžba 0 × x = 5 nema rješenja.

Ako A¹ 0, x =- rješenje jednadžbe.

Odgovor: na A¹ 0, x=

za a = 0 nema rješenja.

Primjer 2. Riješite jednadžbu sjekira – 6 = 2a – 3x.

Riješenje: Ovo je linearna jednadžba, sjekira – 6 = 2a – 3x (1)

sjekira + 3x = 2a +6

Prepisivanje jednadžbe kao (a+3)x = 2(a+3), razmotrite dva slučaja:

a= -3 I A¹ -3.

Ako a= -3, zatim bilo koji realni broj x je korijen jednadžbe (1). Ako A¹ -3 , jednadžba (1) ima jedan korijen x = 2.

Odgovor: Na a = -3, x R ; na A ¹ -3, x = 2.

Primjer 3. Na kojim vrijednostima parametara A među korijenima jednadžbe

2ah – 4kh – a 2 + 4a – 4 = 0 ima više korijena 1 ?

Riješenje: Riješimo jednadžbu 2ah – 4kh – a 2 + 4a – 4 = 0- Linearna jednadžba

2(a - 2) x = a 2 – 4a +4

2(a - 2) x = (a - 2) 2

Na a = 2 rješavanje jednadžbe 0x = 0 bit će bilo koji broj, uključujući onaj veći od 1.

Na A¹ 2 x =
. Po stanju x > 1, to je
>1 i >4.

Odgovor: Na A (2) U (4;∞).

Primjer 4 . Za svaku vrijednost parametra A pronaći broj korijena jednadžbe ah=8.

Riješenje. sjekira = 8- Linearna jednadžba.

g = a– obitelj horizontalnih linija;

g = - Graf je hiperbola. Izgradimo grafove ovih funkcija.

Odgovor: Ako a =0, tada jednadžba nema rješenja. Ako a ≠ 0, tada jednadžba ima jedno rješenje.

Primjer 5 . Pomoću grafova saznajte koliko korijena ima jednadžba:

|x| = ah – 1.

y =| x | ,

g = ah – 1– graf je pravac koji prolazi kroz točku (0;-1).

Izgradimo grafove ovih funkcija.

Odgovor: Kada |a|>1- jedan korijen

na | a|≤1 – jednadžba nema korijena.

Primjer 6 . Riješite nejednadžbu sjekira + 4 > 2x + a 2

Riješenje : sjekira + 4 > 2x + a 2
(a – 2) x >A 2 – 4. Razmotrimo tri slučaja.

Odgovor. x > a + 2 na a > 2; x<а + 2, na A< 2; na a=2 nema rješenja.

§ 2. Kvadratne jednadžbe i nejednadžbe

Kvadratna jednadžba je jednadžba oblika Oh ² + b x + c = 0 , Gdje a≠ 0,

A, b , sa - opcije.

Za rješavanje kvadratnih jednadžbi s parametrom možete koristiti standardne metode rješavanja pomoću sljedećih formula:

1 ) diskriminant kvadratne jednadžbe: D = b ² - 4 ak , (
²- ac)

2) formule za korijene kvadratne jednadžbe:x 1 =
, X 2 =
,

(X 1,2 =
)

Kvadratne nejednakosti nazivaju se

a x 2 + b x + c > 0,a x 2 + b x + c< 0, (1), (2)

a x 2 + b x + c ≥ 0,a x 2 + b x + c ≤ 0,(3), (4)

Skup rješenja nejednadžbe (3) dobiva se kombinacijom skupova rješenja nejednadžbe (1) i jednadžbe , a x 2 + b x + c = 0. Slično se može pronaći i skup rješenja nejednadžbe (4).

Ako je diskriminant kvadratnog trinoma a x 2 + b x + c manji od nule, tada je za a > 0 trinom pozitivan za sve x R.

Ako kvadratni trinom ima korijene (x 1 < х 2 ), tada je za a > 0 pozitivan na skupu(-; x 2 )
(X 2; +) a negativan na intervalu

(x 1; x 2 ). Ako a< 0, то трехчлен положителен на интервале (х 1 ; x 2 ) i negativan za sve x (-; x 1 )
(X 2; +).

Primjer 1. Riješite jednadžbu ax² - 2 (a – 1)x – 4 = 0.

Ovo je kvadratna jednadžba

Riješenje: Posebno značenje a = 0.

Na a = 0 dobivamo linearnu jednadžbu 2x – 4 = 0. Ima jedan korijen x = 2.

Na a ≠ 0. Pronađimo diskriminantu.

D = (a-1)² + 4a = (a+1)²

Ako a = -1, Da D = 0 - jedan korijen.

Nađimo korijen zamjenom a = -1.

-x² + 4x – 4= 0, to je x² -4x + 4 = 0, nalazimo da x=2.

Ako a ≠ - 1, To D >0 . Koristeći formulu korijena dobivamo:x=
;

x 1 =2, x 2 = -.

Odgovor: Na a=0 i a= -1 jednadžba ima jedan korijen x = 2; na a ≠ 0 i

A ≠ - 1 jednadžba ima dva korijenax 1 =2, x 2 =-.

Primjer 2. Odredite broj korijena ove jednadžbe x²-2x-8-a=0 ovisno o vrijednostima parametara A.

Riješenje. Prepišimo ovu jednadžbu u obliku x²-2x-8=a

g = x²-2x-8- graf je parabola;

g =a- obitelj horizontalnih linija.

Izgradimo grafove funkcija.

Odgovor: Kada A<-9 , jednadžba nema rješenja; kada je a=-9, jednadžba ima jedno rješenje; na a> -9, jednadžba ima dva rješenja.

Primjer 3. Na što A nejednakost (a – 3) x 2 – 2ax + 3a – 6 >0 vrijedi za sve vrijednosti x?

Riješenje. Kvadratni trinom je pozitivan za sve vrijednosti x if

a-3 > 0 i D<0, т.е. при а, удовлетворяющих системе неравенств

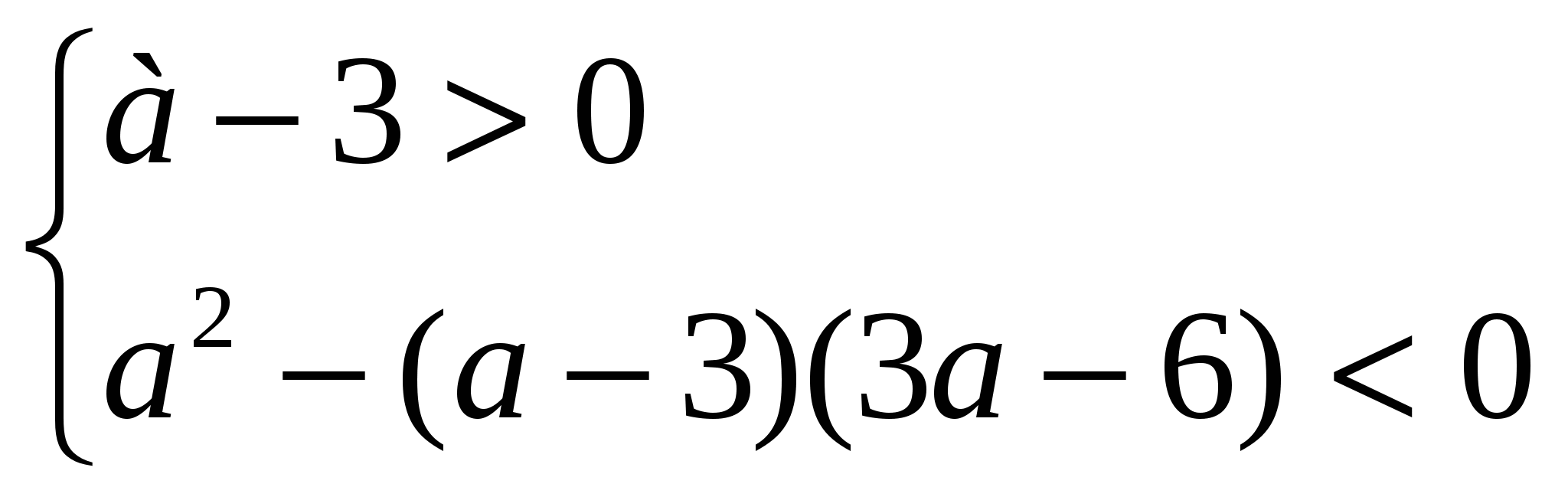
, odakle slijedi daa > 6 .

Odgovor.a > 6

§ 3. Razlomljene racionalne jednadžbe s parametrom,

svodivo na linearno

Postupak rješavanja razlomačkih jednadžbi provodi se prema uobičajenoj shemi: razlomak se zamjenjuje cijelim brojem množenjem obje strane jednadžbe zajedničkim nazivnikom njezine lijeve i desne strane. Nakon toga se rješava cijela jednadžba, isključujući strane korijene, odnosno brojeve koji nazivnik pretvaraju u nulu.

U slučaju jednadžbi s parametrom, ovaj problem je složeniji. Ovdje je za “eliminiranje” stranih korijena potrebno pronaći vrijednost parametra koja zajednički nazivnik stavlja na nulu, odnosno riješiti odgovarajuće jednadžbe za parametar.

Primjer 1. Riješite jednadžbu
= 0

Riješenje: D.Z: x +2 ≠ 0, x ≠ -2

x – a = 0, x = a.

Odgovor: Na a ≠ - 2, x=a

Na a = -2 nema korijena.

Primjer 2 . Riješite jednadžbu
-
=
(1)

Ovo je razlomljena racionalna jednadžba

Riješenje: Značenje a = 0 je poseban. Na a = 0 jednadžba nema smisla i stoga nema korijena. Ako a ≠ 0, tada će jednadžba nakon transformacije imati oblik: x² + 2 (1-a) x + a² - 2a – 3 = 0 (2)- kvadratna jednadžba.

Pronađimo diskriminantu = (1 – a)² - (a² - 2a – 3)= 4, pronaći korijene jednadžbex 1 = a + 1, x 2 = a - 3.

Prelaskom s jednadžbe (1) na jednadžbu (2) domena definicije jednadžbe (1) se proširila, što može dovesti do pojave stranih korijena. Stoga je provjera nužna.

Ispitivanje. Isključimo iz pronađenih vrijednosti x one u kojima

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

Ako x 1 +1=0, to je (a+1) + 1= 0, To a= -2. Tako,

na a= -2 , x 1 -

Ako x 1 +2=0, to je (a+1)+2=0, Da a = - 3. Dakle, kada a = - 3, x 1 - vanjski korijen jednadžbe. (1).

Ako x 2 +1=0, to je (a – 3) + 1= 0, To a = 2. Dakle, kada a = 2 x 2 - vanjski korijen jednadžbe (1).

Ako x 2 +2=0, to je ( a – 3) + 2 = 0, Da a=1. Dakle, kada a = 1,

x 2 - vanjski korijen jednadžbe (1).

U skladu s tim, kada a = - 3 dobivamo x = - 3 – 3 = -6;

na a = - 2 x = -2 – 3= - 5;

na a = 1 x =1 + 1= 2;

na a = 2 x = 2+1 = 3.

Možete zapisati odgovor.

Odgovor: 1) ako a= -3, Da x= -6; 2) ako a= -2, To x= -5; 3) ako a= 0, tada nema korijena; 4) ako a= 1, To x=2; 5) ako a=2, To x=3; 6) ako a ≠ -3, a ≠ -2, a ≠ 0, a ≠ 1, a ≠ 2, zatim x 1 = a + 1, x 2 = a-3.

§4. Iracionalne jednadžbe i nejednadžbe

Jednadžbe i nejednadžbe u kojima je varijabla sadržana pod predznakom korijena nazivaju se iracionalan.

Rješavanje iracionalnih jednadžbi svodi se na prijelaz s iracionalne na racionalnu jednadžbu potenciranjem obje strane jednadžbe ili zamjenom varijable. Kada se obje strane jednadžbe podignu na jednaku potenciju, mogu se pojaviti strani korijeni. Stoga, kada koristite ovu metodu, trebali biste provjeriti sve pronađene korijene zamjenom u izvornu jednadžbu, uzimajući u obzir promjene u vrijednostima parametara.

Jednadžba oblika
=g (x) je ekvivalentan sustavu

Nejednakost f (x) ≥ 0 slijedi iz jednadžbe f (x) = g 2 (x).

Pri rješavanju iracionalnih nejednadžbi koristit ćemo sljedeće ekvivalentne transformacije:

≤ g(x)


≥g(x)

Primjer 1. Riješite jednadžbu
= x + 1 (3)

Ovo je iracionalna jednadžba

Riješenje: Po definiciji aritmetičkog korijena, jednadžba (3) je ekvivalentna sustavu
.

Na a = 2 prva jednadžba sustava ima oblik 0 x = 5, odnosno nema rješenja.

Na a≠ 2 x=
. Saznajmo na kojim vrijednostimaA pronađena vrijednostx zadovoljava nejednakostx ≥ -1:
≥ - 1,
≥ 0,

gdje a ≤ ili a > 2.

Odgovor: Na a≤, a > 2 x=
, na < а ≤ 2 jednadžba nema rješenja.

Primjer 2. Riješite jednadžbu
= a (Dodatak 4)

Riješenje. g =

g = a– obitelj horizontalnih linija.

Izgradimo grafove funkcija.

Odgovor: na A<0 – nema rješenja;

na A≥ 0 - jedno rješenje.

Primjer 3 . Riješimo nejednadžbu(a+1)
<1.

Riješenje. O.D.Z. x ≤ 2. Ako a+1 ≤0, tada nejednakost vrijedi za sve dopustive vrijednosti x. Ako a+1>0, To

(a+1)
<1.

<

gdje x (2-
2

Odgovor. x (- ;2na a (-;-1, x (2-
2

na A (-1;+).

§ 5. Trigonometrijske jednadžbe i nejednadžbe.

Ovdje su formule za rješavanje najjednostavnijih trigonometrijskih jednadžbi:

Sinx = a
x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = a
x = ±arccos a + 2 πn, n Z, ≤1. (2)

Ako >1, onda jednadžbe (1) i (2) nemaju rješenja.

tan x = a
x= arctan a + πn, n Z, a R

ctg x = a
x = arcctg a + πn, n Z, a R

Za svaku standardnu ​​nejednadžbu naznačimo skup rješenja:

1. sin x > a
arcsin a + 2 πn Z,

na a <-1, x R ; na a ≥ 1, nema rješenja.

2. . grijeh x< a
π - arcsin a + 2 πnZ,

za a≤-1, nema rješenja; za a > 1,x R

3. cos x > a
- arccos a + 2 πn < x < arccos a + 2 πn , n Z ,

na A<-1, x R ; na a ≥ 1 , nema rješenja.

4. cos x arccos a+ 2 πnZ,

na a≤-1 , nema rješenja; naa > 1, x R

5. tan x > a, arctan a + πnZ

6.tg x< a, -π/2 + πn Z

Primjer 1. Pronaći A, za koju ova jednadžba ima rješenje:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Riješenje. Zapišimo jednadžbu u obliku

Sos 2 x + (2 a -4) cosx +(a – 5)(a+1) =0, rješavajući ga kao kvadrat, dobivamo cosx = 5-A I cosx = -a-1.

Jednadžba cosx = 5- A ima ponuđena rješenja -1≤ 5-A ≤1
4≤ A≤ 6, i jednadžba cosx = - a-1 osigurano -1≤ -1-A ≤ 1
-2 ≤ A ≤0.

Odgovor. A -2; 0
4; 6

Primjer 2. Na što bpostoji takva da nejednakost
+ b> 0 vrijedi za sve x ≠πn , n Z .

Riješenje. Stavimo A= 0. Nejednakost vrijedi za b >0. Pokažimo sada da nijedan b ≤0 ne zadovoljava uvjete problema. Doista, dovoljno je staviti x = π /2, Ako A <0, и х = - π /2 na A ≥0.

Odgovor.b>0

§ 6. Eksponencijalne jednadžbe i nejednadžbe

1. Jednadžba h(x) f ( x ) = h(x) g ( x) na h(x) > 0 je ekvivalent skupu dvaju sustava
I

2. U posebnom slučaju (h (x)= a ) jednadžba A f(x) = A g(x) pri A> 0, ekvivalentan je skupu dvaju sustava

I

3. Jednadžba A f(x) = b , Gdje A > 0, a ≠1, b>0, ekvivalentno jednadžbi

f (x )= log a b . Događa se A=1 razmatraju se zasebno.

Rješenje najjednostavnijih eksponencijalnih nejednadžbi temelji se na svojstvu snage. Nejednakost oblikaf(a x ) > 0 korištenjem promjene varijablet= a x svodi na rješavanje sustava nejednadžbi
a zatim na rješavanje odgovarajućih jednostavnih eksponencijalnih nejednadžbi.

Pri rješavanju nestroge nejednadžbe potrebno je skupu rješenja stroge nejednadžbe dodati korijene odgovarajuće jednadžbe. Kao i kod rješavanja jednadžbi u svim primjerima koji sadrže izraz A f (x), pretpostavljamo A> 0. Slučaj A= 1 razmatraju se zasebno.

Primjer 1 . Na što A jednadžba 8 x =
ima samo pozitivne korijene?

Riješenje. Po svojstvu eksponencijalne funkcije s bazom većom od jedan, imamo x>0
8 x >1

>1

>0, odaklea (1,5;4).

Odgovor. a (1,5;4).

Primjer 2. Riješite nejednadžbu a 2 ∙2 x > a

Riješenje. Razmotrimo tri slučaja:

1. A< 0 . Budući da je lijeva strana nejednadžbe pozitivna, a desna negativna, nejednakost vrijedi za bilo koji x R.

2. a=0. Nema rješenja.

3. A > 0 . a 2 ∙2 x >a
2 x >
x > -log 2 a

Odgovor. x R na A > 0; nema rješenja za a =0; x (- log 2 a; +) naa> 0 .

§ 7. Logaritamske jednadžbe i nejednadžbe

Predstavimo neke ekvivalencije koje se koriste u rješavanju logaritamske jednadžbe i nejednadžbe.

1. Jednadžba log f (x) g (x) = log f (x) h (x) ekvivalentna je sustavu

Konkretno, ako A >0, A≠1, dakle

log a g(x)=log a h(x)

2. Jednadžba log a g(x)=b
g(x)=a b ( A >0, a ≠ 1, g(x) >0).

3. Nejednakost log f ( x ) g (x) ≤ log f ( x ) h(x) ekvivalentan je kombinaciji dvaju sustava:
I

ako a, b su brojevi, a >0, a ≠1, tada

log a f(x) ≤ b

log a f(x)>b

Primjer 1. Riješite jednadžbu

Riješenje. Nađimo ODZ: x > 0, x ≠ A 4 , a > 0, A≠ 1. Transformirajte jednadžbu

log x – 2 = 4 – log a x
log x + log a x– 6 = 0, odakle log a x = - 3

x = A-3 i log a x = 2
x = A 2. Uvjet x = A 4
A – 3 = A 4 ili A 2 = A 4 ne izvodi se na ODZ.

Odgovor: x = A-3, x = A 2 at A (0; 1)
(1; ).

Primjer 2 . Pronađite najveću vrijednost A, za koju je jednadžba

2 log -
+ a = 0 ima rješenja.

Riješenje. Napravit ćemo zamjenu
= ti dobivamo kvadratnu jednadžbu 2t 2 – t + a = 0. Rješavajući, nalazimoD = 1-8 a . Razmotrimo D≥0, 1-8 A ≥0
A ≤.

Na A = kvadratna jednadžba ima korijent= >0.

Odgovor. A =

Primjer 3 . Riješite nejednadžbulog(x 2 – 2 x + a ) > - 3

Riješenje. Riješimo sustav nejednadžbi

Korijeni kvadratnih trinoma x 1,2 = 1 ±
njihov 3,4 = 1 ±
.

Vrijednosti kritičnih parametara: A= 1 i A= 9.

Neka su onda X 1 i X 2 skupovi rješenja prve i druge nejednadžbe

X 1
x 2 = X – rješenje izvorne nejednadžbe.

U 0< a <1 Х 1 = (- ;1 -
)
(1 +
; +), naA> 1 X 1 = (-;+).

U 0< a < 9 Х 2 = (1 -
; 1 +
), naA≥9 X 2 – nema rješenja.

Razmotrimo tri slučaja:

1. 0< a ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < a < 9 Х = (1 -
;1 +
).

3. a≥ 9 X – nema rješenja.

Ciljevi jedinstvenog državnog ispita

Visoka razina C1, C2

Primjer 1. Pronađite sve vrijednosti R, za koju je jednadžba

R ∙ ctg 2x+2sinx+ str= 3 ima barem jedan korijen.

Riješenje. Transformirajmo jednadžbu

R ∙ (
- 1) + 2sinx + str= 3, sinx = t, t
, t 0.

- str+2t+ str = 3, + 2 t = 3, 3 -2t = , 3t 2 – 2t 3 = str .

Neka f(g) = 3 t 2 – 2 t 3 . Pronađimo skup vrijednosti funkcijef(x) uključeno


. na / = 6 t – 6 t 2 , 6 t - 6 t 2 = 0, t 1 =0, t 2 = 1. f(-1) = 5, f(1) = 1.

Na t
, E(f) =
,

Na t
, E(f) =
, odnosno kada t


, E(f) =
.

Na jednadžbu 3t 2 – 2 t 3 = str (dakle dano) imao barem jedan korijen potreban i dovoljanstr E(f), to je str
.

Odgovor.
.

Primjer 2.

Na kojim vrijednostima parametaraA jednadžba log
(4 x 2 – 4 a + a 2 +7) = 2 ima točno jedan korijen?

Riješenje. Pretvorimo jednadžbu u ekvivalent ovoj:

4x 2 – 4 a + a 2 +7 = (x 2 + 2) 2.

Imajte na umu da ako je određeni broj x korijen rezultirajuće jednadžbe, tada je i broj – x korijen ove jednadžbe. Po uvjetu to nije izvedivo, pa je jedini korijen broj 0.

Naći ćemo A.

4∙ 0 2 - 4a + a 2 +7 = (0 2 + 2) 2 ,

a 2 - 4a +7 = 4, a 2 - 4a +3 = 0, a 1 = 1, a 2 = 3.

Ispitivanje.

1) a 1 = 1. Tada jednadžba izgleda ovako:log
(4 x 2 +4) =2. Idemo to riješiti

4x 2 + 4 = (x 2 + 2) 2, 4x 2 + 4 = x 4 + 4x 2 + 4, x 4 = 0, x = 0 je jedini korijen.

2) a 2 = 3. Jednadžba izgleda ovako:log
(4 x 2 +4) =2
x = 0 je jedini korijen.

Odgovor. 1; 3

Visoka razina C4, C5

Primjer 3. Pronađite sve vrijednosti R, za koje jednadžba

x 2 – ( R+ 3)x + 1= 0 ima korijene cijelog broja i ti korijeni su rješenja nejednadžbe: x 3 – 7 R x 2 + 2x 2 – 14 R x - 3x +21 R ≤ 0.

Riješenje. Neka x 1, x 2 – cjelobrojni korijeni jednadžbe x 2 – (R + 3)x + 1= 0. Tada su prema Vietinoj formuli jednakosti x 1 + x 2 = R + 3, x 1 ∙ x 2 = 1. Umnožak dvaju cijelih brojeva x 1 , X 2 može biti jednak jedinici samo u dva slučaja: x 1 = x 2 = 1 ili x 1 = x 2 = - 1. Ako je x 1 = x 2 = 1, tadaR + 3 = 1+1 = 2
R = - 1; ako x 1 = x 2 = - 1, dakleR + 3 = - 1 – 1 = - 2
R = - 5. Provjerimo jesu li korijeni jednadžbe x 2 – (R + 3)x + 1= 0 u opisanim slučajevima rješenjima ove nejednadžbe. Za tu prilikuR = - 1, x 1 = x 2 = 1 imamo

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – točno; za tu priliku R= - 5, x 1 = x 2 = - 1 imamo (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 – točno. Dakle, zadovoljeni su samo uvjeti problema R= - 1 i R = - 5.

Odgovor.R 1 = - 1 i R 2 = - 5.

Primjer 4. Pronađite sve pozitivne vrijednosti parametra A, za koji broj 1 pripada domeni definicije funkcije

na = (A
- A
).

Vrsta posla: 18

Stanje

Za koje vrijednosti parametra a vrijedi nejednakost

\log_(5)(4+a+(1+5a^(2)-\cos^(2)x) \cdot\sin x - a \cos 2x) \leq 1 je zadovoljeno za sve vrijednosti x?

Prikaži rješenje

Riješenje

Ova nejednakost je ekvivalentna dvostrukoj nejednakosti 0 < 4+a+(5a^{2}+\sin^{2}x) \sin x+ a(2 \sin^(2)x-1) \leq 5 .

Neka \sin x=t , tada dobivamo nejednakost:

4 < t^{3}+2at^{2}+5a^{2}t \leq 1 \: (*) , koji se mora izvršiti za sve vrijednosti od -1 \leq t \leq 1 . Ako je a=0, tada nejednakost (*) vrijedi za bilo koji t\in [-1;1] .

Neka je \neq 0 . Funkcija f(t)=t^(3)+2at^(2)+5a^(2)t raste na intervalu [-1;1] , budući da je derivacija f"(t)=3t^(2) +4at +5a^(2) > 0 za sve vrijednosti t \in \mathbb(R) i a \neq 0 (diskriminant D< 0 и старший коэффициент больше нуля).

Nejednakost (*) bit će zadovoljena za t \in [-1;1] pod uvjetima

\begin(cases) f(-1) > -4, \\ f(1) \leq 1, \\ a \neq 0; \end(cases)\: \Lijeva desna strelica \begin(cases) -1+2a-5a^(2) > -4, \\ 1+2a+5a^(2) \leq 1, \\ a \neq 0; \end(cases)\: \Lijeva desna strelica \početak(slučajevi) 5a^(2)-2a-3< 0, \\ 5a^{2}+2a \leq 0, \\ a \neq 0; \end{cases}\: \Leftrightarrow -\frac(2)(5)\leq a< 0 .

Dakle, uvjet je zadovoljen kada je -\frac(2)(5) \leq a \leq 0 .

Odgovor

\lijevo [ -\frac(2)(5); 0\desno ]

Izvor: “Matematika. Pripreme za Jedinstveni državni ispit 2016. Razina profila." ur. F. F. Lysenko, S. Yu. Kulabukhova.

Vrsta posla: 18
Tema: Nejednadžbe s parametrom

Stanje

Pronađite sve vrijednosti parametra a, za svaku od kojih postoji nejednakost

x^2+3|x-a|-7x\leqslant -2a

ima jedinstveno rješenje.

Prikaži rješenje

Riješenje

Nejednakost je ekvivalentna skupu sustava nejednakosti

\lijevo[\!\!\begin(array)(l) \begin(cases) x \geqslant a, \\ x^2+3x-3a-7x+2a\leqslant0; \kraj(slučajevi) \\ \početak(slučajevi)x \lijevo[\!\!\begin(array)(l) \begin(cases) x \geqslant a, \\ x^2-4x-a\leqslant0; \kraj(slučajevi) \\ \početak(slučajevi)x \lijevo[\!\!\begin(array)(l) \begin(cases) a \leqslant x, \\ a\geqslant x^2-4x; \end(cases) \\ \begin(cases)a>x, \\ a\leqslant -\frac(x^2)(5)+2x. \end(cases)\end(array)\right.

U Oxa koordinatnom sustavu ćemo konstruirati grafove funkcija a=x, a=x^2-4x, a=-\frac(x^2)(5)+2x.

Rezultirajući skup zadovoljavaju točke unutar grafova funkcija a=x^2-4x, a=-\frac(x^2)(5)+2x na intervalu x\in (osjenčano područje).

Iz grafikona utvrđujemo: izvorna nejednadžba ima jedinstveno rješenje za a=-4 i a=5, jer će u osjenčanom području biti jedna točka s ordinatom a jednakom -4 i jednakom 5.

Tečajni rad

Izvođač: Bugrov S K.

Proučavanje mnogih fizičkih procesa i geometrijskih uzoraka često dovodi do rješavanja problema s parametrima. Neka sveučilišta također uključuju jednadžbe, nejednadžbe i njihove sustave u ispitne radove, koji su često vrlo složeni i zahtijevaju nestandardan pristup rješavanju. U školi se ovaj jedan od najtežih dijelova školskoga matematičkog tečaja razmatra tek na nekoliko izbornih sati.

U pripremi ovog rada, postavio sam cilj dubljeg proučavanja ove teme, pronalaženja najracionalnijeg rješenja koje brzo dovodi do odgovora. Po mom mišljenju, grafička metoda je zgodan i brz način za rješavanje jednadžbi i nejednadžbi s parametrima.

Moj esej obrađuje često susrećene vrste jednadžbi, nejednakosti i njihovih sustava, te se nadam da će mi znanje koje sam stekao u procesu rada pomoći pri polaganju školskih ispita i pri upisu na fakultet.

§ 1. Osnovne definicije

Razmotrimo jednadžbu

¦(a, b, c, …, k, x)=j(a, b, c, …, k, x), (1)

gdje su a, b, c, …, k, x varijabilne veličine.

Svaki sustav promjenjivih vrijednosti

a = a0, b = b0, c = c0, …, k = k0, x = x0,

u kojem i lijeva i desna strana ove jednadžbe poprimaju stvarne vrijednosti naziva se sustav dopuštenih vrijednosti varijabli a, b, c, ..., k, x. Neka je A skup svih dopuštenih vrijednosti od a, B je skup svih dopuštenih vrijednosti od b, itd., X je skup svih dopuštenih vrijednosti od x, tj. aOA, bOB, …, xOX. Ako za svaki od skupova A, B, C, …, K izaberemo i fiksiramo jednu vrijednost a, b, c, …, k i zamijenimo ih u jednadžbu (1), tada ćemo dobiti jednadžbu za x, tj. jednadžba s jednom nepoznatom.

Varijable a, b, c, ..., k, koje se pri rješavanju jednadžbe smatraju konstantama, nazivamo parametrima, a samu jednadžbu nazivamo jednadžbom koja sadrži parametre.

Parametri su označeni prvim slovima latinične abecede: a, b, c, d, ..., k, l, m, n, a nepoznanice su označene slovima x, y, z.

Riješiti jednadžbu s parametrima znači naznačiti pri kojim vrijednostima parametara rješenja postoje i kakva su.

Dvije jednadžbe koje sadrže iste parametre nazivaju se ekvivalentnim ako:

a) imaju smisla za iste vrijednosti parametara;

b) svako rješenje prve jednadžbe je rješenje druge i obrnuto.

§ 2. Algoritam rješenja.

Odredi domenu definicije jednadžbe.

Izražavamo a kao funkciju od x.

U koordinatnom sustavu xOa konstruiramo graf funkcije a=¦(x) za one vrijednosti x koje su uključene u domenu definicije ove jednadžbe.

Nađemo presječne točke pravca a=c, gdje je cÎ(-¥;+¥) s grafom funkcije a=¦(x).Ako pravac a=c siječe graf a=¦(x) , zatim odredimo apscisu presječnih točaka. Da biste to učinili, dovoljno je riješiti jednadžbu a=¦(x) za x.

Zapisujemo odgovor.

I. Riješite jednadžbu

(1)

Budući da x=0 nije korijen jednadžbe, jednadžba se može riješiti za:

ili

Graf funkcije su dvije "zalijepljene" hiperbole. Broj rješenja izvorne jednadžbe određen je brojem sjecišta konstruiranog pravca i pravca y=a.

Ako je O (-¥;-1]P(1;+¥)P

, tada pravac y=a siječe graf jednadžbe (1) u jednoj točki. Apscisu ove točke ćemo pronaći pri rješavanju jednadžbe za x.

Dakle, na tom intervalu jednadžba (1) ima rješenje

. , tada pravac y=a siječe graf jednadžbe (1) u dvije točke. Apscise tih točaka mogu se pronaći iz jednadžbi i , dobivamo i . , tada pravac y=a ne siječe graf jednadžbe (1), stoga nema rješenja.

Ako je O (-¥;-1]P(1;+¥)P

, To ; , To , ; , onda nema rješenja.

II. Pronađite sve vrijednosti parametra a za koje vrijedi jednadžba

ima tri različita korijena.

Prepisivanje jednadžbe kao

i nakon što ispitate par funkcija, možete primijetiti da će željene vrijednosti parametra a i samo one odgovarati onim položajima grafa funkcije na kojima ima točno tri točke sjecišta s grafom funkcije .

U koordinatnom sustavu xOy konstruirat ćemo graf funkcije

). Da bismo to učinili, možemo je predstaviti u obliku i, razmatrajući četiri slučaja koja se pojavljuju, zapisujemo ovu funkciju u obliku

Budući da je graf funkcije

- ovo je ravna crta koja ima kut nagiba prema osi Ox jednak , a sijekući os Oy u točki s koordinatama (0, a), zaključujemo da se tri navedene sjecišne točke mogu dobiti samo u slučaju kada ova linija dodiruje graf funkcije. Stoga nalazimo izvod.

III. Pronađite sve vrijednosti parametra a, za svaku od njih sustav jednadžbi

ima rješenja.

Iz prve jednadžbe sustava dobivamo

pri Stoga ova jednadžba definira obitelj "poluparabola" - desne grane parabole "klize" sa svojim vrhovima duž apscisne osi.

Odaberimo potpune kvadrate na lijevoj strani druge jednadžbe i faktorizirajmo ih

Mnogo točaka ravnine

zadovoljavaju drugu jednadžbu dvije ravne linije i

Otkrijmo pri kojim vrijednostima parametra a krivulja iz obitelji "poluparabola" ima barem jednu zajedničku točku s jednom od rezultirajućih ravnih linija.

Rješavanje nejednadžbi s parametrom.

Nejednadžbe koje imaju oblik ax > b, ax< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются linearne nejednakosti.

Načela za rješavanje linearnih nejednadžbi s parametrom vrlo su slična načelima za rješavanje linearnih jednadžbi s parametrom.

Primjer 1.

Riješite nejednadžbu 5x – a > ax + 3.

Riješenje.

Prvo, transformirajmo izvornu nejednadžbu:

5x – ax > a + 3, izbacimo x iz zagrada na lijevoj strani nejednakosti:

(5 – a)x > a + 3. Sada razmotrite moguće slučajeve za parametar a:

Ako je a > 5, tada je x< (а + 3) / (5 – а).

Ako je a = 5, tada rješenja nema.

Ako a< 5, то x >(a + 3) / (5 – a).

Ovo rješenje će biti odgovor na nejednakost.

Primjer 2.

Riješite nejednadžbu x(a – 2) / (a ​​​​– 1) – 2a/3 ≤ 2x – a za a ≠ 1.

Riješenje.

Transformirajmo izvornu nejednakost:

x(a – 2) / (a ​​​​– 1) – 2x ≤ 2a/3 – a;

Ah/(a – 1) ≤ -a/3. Množenjem obje strane nejednakosti s (-1), dobivamo:

ax/(a – 1) ≥ a/3. Istražimo moguće slučajeve za parametar a:

1 slučaj. Neka je a/(a – 1) > 0 ili a € (-∞; 0)ᴗ(1; +∞). Tada je x ≥ (a – 1)/3.

Slučaj 2. Neka je a/(a – 1) = 0, tj. a = 0. Tada je x bilo koji realan broj.

Slučaj 3. Neka je a/(a – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Odgovor: x € [(a – 1)/3; +∞) za € (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] za € (0; 1);
x € R za a = 0.

Primjer 3.

Riješite nejednadžbu |1 + x| ≤ ax u odnosu na x.

Riješenje.

Iz uvjeta proizlazi da desna strana osi nejednakosti mora biti nenegativna, tj. ax ≥ 0. Pravilom otkrivanja modula iz nejednadžbe |1 + x| ≤ ax imamo dvostruku nejednakost

Ax ≤ 1 + x ≤ ax. Prepišimo rezultat u obliku sustava:

(ax ≥ 1 + x;
(-ax ≤ 1 + x.

Pretvorimo ga u:

((a – 1)x ≥ 1;
((a + 1)x ≥ -1.

Proučavamo dobiveni sustav na intervalima iu točkama (Sl. 1):

Za a ≤ -1 x € (-∞; 1/(a – 1)].

Na -1< а < 0 x € [-1/(а – 1); 1/(а – 1)].

Kada je a = 0 x = -1.

U 0< а ≤ 1 решений нет.

Grafička metoda rješavanja nejednadžbi

Iscrtavanje grafova uvelike pojednostavljuje rješavanje jednadžbi koje sadrže parametar. Korištenje grafičke metode pri rješavanju nejednadžbi s parametrom još je preglednije i svrsishodnije.

Grafičko rješavanje nejednadžbi oblika f(x) ≥ g(x) znači pronalaženje vrijednosti varijable x za koje graf funkcije f(x) leži iznad grafa funkcije g(x). Za to je uvijek potrebno pronaći sjecišne točke grafova (ako postoje).

Primjer 1.

Riješite nejednadžbu |x + 5|< bx.

Riješenje.

Gradimo grafove funkcija y = |x + 5| i y = bx (slika 2). Rješenje nejednadžbe bit će one vrijednosti varijable x za koje je graf funkcije y = |x + 5| bit će ispod grafa funkcije y = bx.

Na slici je prikazano:

1) Za b > 1 pravci se sijeku. Apscisa sjecišta grafova ovih funkcija je rješenje jednadžbe x + 5 = bx, odakle je x = 5/(b – 1). Graf y = bx nalazi se iznad na x od intervala (5/(b – 1); +∞), što znači da je ovaj skup rješenje nejednadžbe.

2) Slično nalazimo da je na -1< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) Za b ≤ -1 x € (-∞; 5/(b – 1)).

4) Za 0 ≤ b ≤ 1 grafovi se ne sijeku, što znači da nejednadžba nema rješenja.

Odgovor: x € (-∞; 5/(b – 1)) za b ≤ -1;
x € (-5/(b + 1); 5/(b – 1)) na -1< b < 0;
nema rješenja za 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) za b > 1.

Primjer 2.

Riješite nejednadžbu a(a + 1)x > (a + 1)(a + 4).

Riješenje.

1) Pronađimo "kontrolne" vrijednosti za parametar a: a 1 = 0 i 2 = -1.

2) Riješimo ovu nejednadžbu na svakom podskupu realnih brojeva: (-∞; -1); (-1); (-10); (0); (0; +∞).

a)a< -1, из данного неравенства следует, что х >(a + 4)/a;

b) a = -1, tada će ova nejednadžba imati oblik 0 x > 0 – nema rješenja;

c) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, tada ova nejednadžba ima oblik 0 x > 4 – nema rješenja;

e) a > 0, iz ove nejednakosti slijedi da je x > (a + 4)/a.

Primjer 3.

Riješite nejednadžbu |2 – |x||< a – x.

Riješenje.

Gradimo graf funkcije y = |2 – |x|| (slika 3) i razmotriti sve moguće slučajeve položaja pravca y = -x + a.

Odgovor: nejednadžba nema rješenja za a ≤ -2;
x € (-∞; (a – 2)/2) za a € (-2; 2];
x € (-∞; (a + 2)/2) za a > 2.

Pri rješavanju raznih problema, jednadžbi i nejednadžbi s parametrima otkriva se značajan broj heurističkih tehnika koje se potom mogu uspješno primijeniti u bilo kojoj drugoj grani matematike.

Problemi s parametrima igraju važnu ulogu u formiranju logičkog mišljenja i matematičke kulture. Zato ćete se, svladavši metode rješavanja problema s parametrima, uspješno nositi s drugim problemima.

Još uvijek imate pitanja? Ne znate kako riješiti nejednadžbe?
Dobiti pomoć od učitelja -.
Prvi sat je besplatan!

blog.site, pri kopiranju materijala u cijelosti ili djelomično, poveznica na izvorni izvor je obavezna.

Serija "Učenje rješavanja problema s parametrima"

IV. Kvadratne jednadžbe i nejednadžbe s parametrom

IV.1. Osnovni koncepti

Definicija. Funkcija oblika (1), gdje su , , zadane funkcije parametra A, razmatrane na sjecištu njihovih domena definicije, nazvat ćemo kvadratnom funkcijom s parametrom A.

Primjeri.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .

Definicija. Poddomena definicije kvadratne funkcije (1) s parametrom A razumjet ćemo cijeli skup parova vrijednosti x I A tip ( x; A), za svaki od kojih izraz ne gubi svoje značenje.

Ustanovimo domene definiranja funkcija 1-10.

1. 2. 3. 4. 5.
6. 7. 8. 9. 10.

Ako parametar uzme jednu od numeričkih vrijednosti iz , tada će funkcija (1) imati oblik jedne od funkcija s numeričkim koeficijentima:

; ; ;
; ; ; ,

Gdje k, b, c– realni brojevi.

Obratimo pozornost na činjenicu da za neke vrijednosti parametra iz, kvadratna funkcija s parametrom ima oblik ili kvadratne funkcije bez parametra ili linearne.

Budući da kvadratna funkcija s parametrom najčešće “generira” obitelj kvadratnih ili linearnih funkcija s numeričkim koeficijentima, onda govoreći o grafovi kvadratne funkcije s parametrom, mislit ćemo na mnoge grafove ove obitelji.

Definicija. A naziva se jednadžba oblika (1) gdje su , , te funkcije parametra A, razmatrani na sjecištu njihovih domena definicije.

Konkretno, neki od koeficijenata ili odsječak mogu biti brojevi.

Primjeri.

, (1)
, (2)
, (3)
, (4)
. (5)

Koristeći definiciju kvadratne funkcije s parametrom, možemo dati sljedeću definiciju kvadratne jednadžbe s parametrom.

Definicija. Kvadratna jednadžba s parametrom A naziva se jednadžba oblika , gdje je kvadratna funkcija s parametrom A.

Ako je , tada je jednadžba (1) kvadratna u tradicionalnom smislu, tj. drugi stupanj.
Ako je , tada jednadžba (1) postaje linearna.

Za sve važeće vrijednosti parametara A, za koje i , pomoću poznatih formula dobivamo izraze za korijene jednadžbe (1) u smislu parametra.

Te vrijednosti A, u kojima , treba promatrati zasebno kao posebne slučajeve.
Tako će, primjerice, jednadžba (5) imati oblik , odakle .

IV.2. Kvadratne jednadžbe s parametrom

№1. Riješite jednadžbu.

– jednadžba-posljedica. Dobivamo: , .

U koordinatnom sustavu ( aoh) dovršavamo rješenje. (Sl. 1)

Odgovor: 1. Ako je , onda .

2. Ako je , tada .

3. Ako je , , tada , .

№2. Pronađite vrijednost parametra A, u kojoj jednadžba ima jedan korijen. Ako postoji više takvih vrijednosti, upišite njihov zbroj u svoj odgovor.

Ova se jednadžba svodi na ekvivalentni sustav:

Dovedimo ga u oblik: i riješimo grafički u koordinatnom sustavu ( xOa). (slika 2).

Jednadžba ima jedan korijen u , i .

№3. Pronađite sve vrijednosti x tako da za bilo koju vrijednost parametra A, ne pripada intervalu (0; 2], izraz nije jednak izrazu. (USE-2007).

Preformulirajmo problem: “Nađi sve vrijednosti x tako da za bilo koju vrijednost parametra jednadžba nema korijena."
Izrazimo se A kroz x:

1) Neka . Zatim . Stoga jednadžba ima korijene. To znači da ne zadovoljava uvjet.
2) Neka . Zatim . Koristimo koordinatni sustav ( xOa). (slika 3).

Uvjet je zadovoljen.

№4. Koliko korijena ovisi o parametru A ima jednadžbu?

Proširimo modul:

U koordinatnom sustavu ( xOy) izgradimo graf funkcije

a nekoliko linija olovke paralelnih pravaca zadanih jednadžbom. (slika 4).

Odgovor: 1. Ako , onda nema korijena.

2. Ako je , onda jedan korijen.

3. Ako je , tada postoje dva korijena.

IV.3. Kvadratne nejednadžbe s parametrom

№5. Riješite nejednadžbu .

1 način.

Uzmimo to u obzir. Tada je rješenje ove nejednakosti za bilo koji b.(slika 5).

Ako , tada prelazimo na nejednadžbu čiji će skup rješenja biti prikazan u koordinatnom sustavu ( kutija). (slika 6).

Spojimo smokvu. 5 i 6.

A sada prema Sl. 7, režući ga okomitim ravnim linijama, lako je dobiti odgovor.

Odgovor: 1. Ako je , onda .
2. Ako je , tada .
3. Ako je , onda

Metoda 2.

Riješimo nejednadžbu grafički u koordinatnom sustavu ( xOb):

. (slika 8).

Razmotrimo dva slučaja.

1) . Tada će nejednakost poprimiti oblik gdje je .
2) , zatim .

Graf funkcije i dio ravnine koji sadrži točke čije koordinate zadovoljavaju nejednadžbu prikazani su na slici 8.

1. Ako je , onda .
2. Ako je , tada . 3. Ako je , tada .

3 načina.

Prikažimo sada grafičko rješenje u koordinatnom sustavu ( xOy). Da bismo to učinili, proširimo modul:

Razmotrite funkciju .

Korijeni kvadratnog trinoma .

Usporedimo i .

1) , odakle .

Dobivamo ukupnost. (Sl. 9)

2) , odakle . (slika 10).

Zatim tj. .

3) , odakle . (slika 11).

Zatim tj. .

Odgovor: 1. Ako je , onda .

2. Ako je , tada .
3. Ako je , tada .

№6. Pronađite sve vrijednosti parametara A, za koju je najmanja vrijednost funkcije više od 2.

Dovoljno je pronaći sve vrijednosti parametra A, za svaki od kojih je nejednakost istinita za bilo koji . Prepišimo nejednakost u obliku ., ;