Ekstremne točke funkcije na spletu. Ekstremum funkcije dveh spremenljivk
Iz tega članka bo bralec izvedel, kaj je ekstrem funkcionalne vrednosti, pa tudi o značilnostih njegove uporabe v praktičnih dejavnostih. Preučevanje takšnega koncepta je izjemno pomembno za razumevanje temeljev višje matematike. Ta tema je temeljna za poglobljeno študijo predmeta.
V stiku z
Kaj je ekstrem?
V šolskem tečaju je podanih veliko definicij pojma "ekstrem". Ta članek je namenjen najglobljemu in najjasnejšemu razumevanju izraza za tiste, ki tega vprašanja ne poznajo. Torej izraz pomeni, koliko funkcionalna vrzel pridobi minimalno oz največja vrednost na enem ali drugem nizu.
Ekstremum je tako najmanjša vrednost funkcije kot maksimum hkrati. Obstajata najnižja in najvišja točka, to je skrajne vrednosti argumenta na grafu. Glavne vede, ki uporabljajo ta koncept, so:
- statistika;
- krmiljenje stroja;
- ekonometrija.
Ekstremne točke igrajo pomembno vlogo pri določanju zaporedja dane funkcije. Koordinatni sistem na grafu v v najboljšem primeru prikazuje spremembo skrajnega položaja glede na spremembo funkcionalnosti.
Ekstremumi odvodne funkcije
Obstaja tudi tak pojav, kot je "izpeljanka". Treba je določiti ekstremno točko. Pomembno je, da minimalnih ali maksimalnih točk ne zamenjujete z najvišjimi in najnižjimi vrednostmi. To sta različna koncepta, čeprav se morda zdita podobna.
Vrednost funkcije je glavni dejavnik pri določanju, kako najti največjo točko. Izpeljanka ni oblikovana iz vrednosti, ampak izključno iz njenega skrajnega položaja v enem ali drugem redu.
Sama izpeljanka se določi na podlagi teh ekstremnih točk in ne na največji ali najmanjši vrednosti. V ruskih šolah meja med tema dvema konceptoma ni jasno potegnjena, kar vpliva na razumevanje te teme na splošno.
Razmislimo zdaj o konceptu "akutni ekstrem". Danes obstajata akutna minimalna vrednost in akutna maksimalna vrednost. Definicija je podana v skladu z rusko klasifikacijo kritičnih točk funkcije. Koncept ekstremne točke je osnova za iskanje kritičnih točk na grafu.

Za opredelitev takega koncepta se zatečejo k uporabi Fermatovega izreka. Je najpomembnejši pri preučevanju ekstremnih točk in daje jasno predstavo o njihovem obstoju v takšni ali drugačni obliki. Da bi zagotovili ekstremnost, je pomembno ustvariti določene pogoje za zmanjšanje ali povečanje na grafu.
Če želite natančno odgovoriti na vprašanje "kako najti največjo točko", morate upoštevati te smernice:
- Iskanje natančne domene definicije na grafu.
- Iskanje odvoda funkcije in ekstremne točke.
- Rešite standardne neenačbe za domeno, kjer je argument.
- Znati dokazati, v katerih funkcijah je točka na grafu definirana in zvezna.

Pozor! Iskanje kritične točke funkcije je možno le, če obstaja odvod vsaj drugega reda, kar je zagotovljeno z visokim deležem prisotnosti ekstremne točke.
Nujen pogoj za ekstrem funkcije
Za obstoj ekstrema je pomembno, da obstajata minimalna in maksimalna točka. Če je to pravilo le delno upoštevano, je pogoj za obstoj ekstrema kršen.

Vsako funkcijo v kateri koli poziciji je treba razlikovati, da bi prepoznali njene nove pomene. Pomembno je razumeti, da primer točke, ki gre proti nič, ni glavno načelo za iskanje diferencibilne točke.
Akutni ekstrem, kot tudi minimum funkcije, je izjemno pomemben vidik reševanja matematičnega problema z uporabo ekstremnih vrednosti. Da bi bolje razumeli to komponento, je pomembno, da se sklicujete na tabelarične vrednosti za določanje funkcionalnosti.
| Raziskava polnega pomena | Risanje grafa vrednosti |
| 1. Določitev točk naraščanja in padanja vrednosti. 2. Iskanje diskontinuitetnih točk, ekstremuma in presečišča s koordinatnimi osemi. 3. Postopek določanja sprememb položaja na grafu. 4. Določitev indikatorja in smeri konveksnosti in konveksnosti ob upoštevanju prisotnosti asimptot. 5. Izdelava zbirne tabele raziskave z vidika določanja njenih koordinat. 6. Iskanje intervalov naraščanja in padanja skrajnih in ostrih točk. 7. Določanje konveksnosti in konkavnosti krivulje. 8. Risanje grafa ob upoštevanju raziskav vam omogoča, da najdete minimum ali maksimum. |
Glavni element, ko je potrebno delati z ekstremnimi točkami, je natančna konstrukcija njegovega grafa. Šolski učitelji pogosto ne posvečajo največje pozornosti tako pomembnemu vidiku, ki je huda kršitev izobraževalnega procesa. Konstrukcija grafa se pojavi le na podlagi rezultatov preučevanja funkcionalnih podatkov, prepoznavanja akutnih ekstremov in točk na grafu. Ostri ekstremi odvodne funkcije so prikazani na grafu natančnih vrednosti z uporabo standardni postopek določitev asimptot. Maksimalno in minimalno točko funkcije spremlja več kompleksne konstrukcije grafične umetnosti. To je posledica globlje potrebe po delu skozi problem akutnega ekstrema. Prav tako je treba najti odvod kompleksne in enostavne funkcije, saj je to eden najpomembnejših konceptov v problemu ekstrema. |
Ekstrem funkcionalnega
Če želite najti zgornjo vrednost, morate upoštevati naslednja pravila:
- določiti nujen pogoj za ekstremno razmerje;
- upoštevajte zadosten pogoj skrajnih točk na grafu;
- izvedite izračun akutnega ekstrema.
Uporabljata se tudi koncepta, kot sta šibek minimum in močan minimum. To je treba upoštevati pri določanju ekstrema in njegovem natančnem izračunu. Hkrati je akutna funkcionalnost iskanje in ustvarjanje vseh potrebnih pogojev za delo z grafom funkcije.
Definicija 1. Točka M(x 0 ; y 0) se imenuje največja (minimalna) točka funkcije z = f(x; y), če obstaja soseska točke M taka, da za vse točke (x; y) iz te soseski velja naslednja neenakost:
f(x 0 ; y 0) f(x; y), .
1. izrek
(nujni pogoj za obstoj ekstrema)
. Če diferenciabilna funkcija z = f(x; y) doseže ekstrem v točki M(x 0 ; y 0), potem so njeni parcialni odvodi prvega reda na tej točki enaki nič, tj.  ;
;
Točke, v katerih so delni odvodi enaki nič, imenujemo stacionarni oz kritične točke.
2. izrek (zadostni pogoj za obstoj ekstrema)
Naj bo funkcija z = f(x; y):
a) definirana v neki okolici točke (x 0 ; y 0), v kateri  in
in  ;
;
b) ima na tej točki zvezne parcialne odvode drugega reda
 ;
;


Če je torej = AC B 2 > 0, potem ima v točki (x 0 ; y 0) funkcija z = f(x; y) ekstrem in če je A< 0 (или С < 0) – максимум, если А >0 (ali C > 0) – najmanj. V primeru = AC B 2< 0, функция z = f(x; y) экстремума не имеет. Если = AC B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).
Primer 1. Poiščite ekstrem funkcije z = x 2 + xy + y 2 3x 6y.
rešitev. Poiščimo delne odvode prvega reda:


Uporabimo nujni pogoj za obstoj ekstrema:


Z reševanjem sistema enačb najdemo x in y koordinate stacionarnih točk: x = 0; y = 3, tj. M(0; 3).
Izračunajmo delne odvode drugega reda in poiščimo njihove vrednosti v točki M.
A =  = 2; C =
= 2; C =  = 2;
= 2;
B =  .
.
Sestavimo diskriminanto = AC B 2 = 2 2 1 > 0, A = 2 > 0. Zato ima v točki M(0; 3) podana funkcija minimum. Vrednost funkcije na tej točki je z min = 9.
Poiščite ekstreme funkcij
322. z = x 2 + y 2 + xy 4x 5y 323. z = y 3 x 3 3xy
324. z = x 2 2xy + 4y 3 325. z =  y 2 x + 6y
y 2 x + 6y
326. z = x y (1 x y) 327. z = 2xy 4x 2y
328. z = e x/2 (x + y 2) 329. z = x 3 + 8y 3 6xy + 1
330. z = 3x 2 y x 3 y 4 331. z = 3x + 6y x 2 xy + y 2
Največja in najmanjša vrednost funkcije dveh spremenljivk v zaprti domeni
Da bi našli največji in vsaj vrednosti funkcije v zaprtem območju, morate:
1) poiščite kritične točke na določenem območju in izračunajte vrednosti funkcij na teh točkah;
2) poiščite kritične točke na meji območja in izračunajte največje in najmanjše vrednosti funkcij na njih;
3) izmed vseh najdenih vrednosti izberite največjo in najmanjšo.
Primer 2. Poiščite največjo in najmanjšo vrednost funkcije z =  v krogu x 2 + y 2 1.
v krogu x 2 + y 2 1.
rešitev. Poiščemo koordinate kritičnih točk, ki se nahajajo znotraj obravnavanega območja, za katere izračunamo parcialne odvode funkcije z prvega reda in jih enačimo z nič.




od koder je x = 0, y = 0 in je torej M(0; 0) kritična točka.
Izračunajmo vrednost funkcije z v točki M(0; 0): z(0; 0) = 2.
Poiščemo kritične točke na meji območja - kroga, ki ga določa enačba x 2 + y 2 = 1. Če nadomestimo y 2 = 1 - x 2 v funkcijo z = z(x; y), dobimo funkcijo ene spremenljivke
z =  ;
;
kjer je x[1; 1].
Po izračunu derivata  in jo enačimo z nič, dobimo kritične točke na meji območja x 1 = 0, x 2 =
in jo enačimo z nič, dobimo kritične točke na meji območja x 1 = 0, x 2 =  , x 3 =
, x 3 = 
Poiščimo vrednost funkcije z(x) =  na kritičnih točkah in na koncih segmenta [1; 1]: z(0) = ;
na kritičnih točkah in na koncih segmenta [1; 1]: z(0) = ;  =;
=; ; z(1) = ; z(1) =
; z(1) = ; z(1) = 
Izberimo največjo in najmanjšo med vrednostmi funkcije z na kritičnih točkah znotraj in na meji kroga.
Torej, z max. = z(0; 0) = 2
Pri optimizacijskih problemih je treba najti ekstreme funkcije dveh ali več spremenljivk pod pogojem, da obstaja povezava med spremenljivkami tega razmerja, podana z enačbo ![]() . V tem primeru rečemo, da moramo najti pogojni ekstrem
.
. V tem primeru rečemo, da moramo najti pogojni ekstrem
.
Če želite najti pogojni ekstrem, morate najti delni derivati in se odloči sistemi enačb Obstaja algoritem za iskanje pogojnega ekstrema v treh korakih, ki ga bomo zdaj analizirali na primeru, in geometrijski pomen pogojnega ekstrema, ki bi moral doseči vsakogar pri analizi prav tega primera.
Tako bomo analizirali algoritem na primeru najpogostejšega problema - iskanja pogojnega ekstrema funkcije dveh spremenljivk. .
Korak 1. Predstavljen Lagrangeova funkcija
kjer je prvi člen izvirna funkcija sama, drugi člen z znakom minus pa je leva stran enačbe veznega pogoja, pomnožena z (lambda) - Lagrangeovim množiteljem.
Primer 1. Najti pogojni ekstremi funkcija dveh spremenljivk, ki izražata površino pravokotnika glede na njegove stranice x in l pod pogojem, da obstaja vrv, ki lahko veže ta pravokotnik in je dolžina te vrvi 100.
Korak 1. rešitev. Enačbo pogoja povezave pripeljemo do zahtevane oblike z ničlo na desni strani:
![]() .
.
Sestavljajmo Lagrangeova funkcija:
2. korak Iz enačb sestavimo sistem enačb delni derivati nič in enačba pogoja povezave (nujni znak obstoja pogojnega ekstrema):
Rešitve tega sistema enačb so točke možnega pogojnega ekstrema - stacionarne točke ali, kot pravijo tudi kritične točke.
Primer 1. Korak 2.
rešitev.

x in l :
Zamenjajmo te izraze v tretjo enačbo in poiščimo vrednost Lagrangeovega množitelja:

x in l in poiščite vrednosti spremenljivk izvirne funkcije:

Prejeli smo in. Te vrednosti so tudi koordinate stacionarne točke. Tako smo dobili stacionarno točko.
3. korak Naj bo stacionarna točka, najdena v koraku 2. Če želite ugotoviti, ali je pogojni ekstrem minimum ali maksimum, morate najti drugi diferencial Lagrangeove funkcije
![]()
in v dobljenem izrazu nadomestite namesto "lambda" njegove vrednosti (vrednosti Lagrangeovega množitelja), ki jih najdete v 2. koraku.
Če je vrednost drugega diferenciala Lagrangeove funkcije manjša od nič (), je stacionarna točka maksimalna točka; če je večja od nič (), je stacionarna točka minimalna točka. Če je vrednost drugega diferenciala Lagrangeove funkcije enaka nič, so potrebne dodatne raziskave, vendar se takšni primeri praktično ne pojavljajo pri nalogah, ki jih študenti zadajo.
Koordinate stacionarnih točk zamenjamo v začetno točko in tako končno najdemo pogojni ekstremi (ali minimum in maksimum ali ena od teh skrajnosti).
Primer 1. 3. korak.
rešitev. Poiščimo drugi diferencial Lagrangeove funkcije:
![]()
V našem primeru, ker sta prva in tretja komponenta enaki nič, nam vrednosti Lagrangeovega množitelja ni treba zamenjati vanje. Vendar morate najti razmerje med razlikami dx in dy :
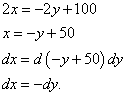
Ker so dobljene vrednosti nasprotnega predznaka, ugotovimo, da v vsakem primeru .
Zdaj lahko najdemo vrednost pogojni ekstrem izvirne funkcije, kar je največ:
![]() .
.
To je največja površina pravokotnika, določena z izvirno funkcijo, ki jo je mogoče omejiti z vrvjo, katere dolžina je 100.
Primer 2. Najti pogojni ekstremi
Korak 1. Sestavljajmo Lagrangeova funkcija:
2. korak Poiščimo parcialne odvode Lagrangeove funkcije in sestavimo sistem enačb iz njihovih enakosti na nič in enačbe veznega pogoja:

Iz prve in druge enačbe izrazimo oz x in l :

Zamenjajmo te izraze v tretjo enačbo in poiščimo vrednosti Lagrangeovega množitelja:

Nadomestimo zdaj vrednost Lagrangeovega množitelja v izraze za x in l in poiščite vrednosti spremenljivk izvirne funkcije za dve vrednosti Lagrangeovega množitelja:

Ti vrednosti x in y sta koordinati dveh stacionarnih točk. Tako smo dobili stacionarne točke ![]() .
.
3. korak Poiščimo parcialne odvode Lagrangeove funkcije drugega reda:
Poiščimo drugi diferencial Lagrangeove funkcije s pomočjo formule
![]() :
:
![]()
Prejeli smo vrednost, manjšo od nič, torej točka - točka pogojni maksimum:
![]() .
.
Določimo predznak drugega diferenciala Lagrangeove funkcije pri vrednosti Lagrangeovega množitelja:
![]()
Prejeli smo vrednost, večjo od nič, torej točka - točka pogojni minimum:
![]() .
.
torej pogojni ekstremi so dane funkcije najdene.
Primer 3. Najti pogojni ekstremi funkcije dveh spremenljivk, za katere velja .
Korak 1. Sestavljajmo Lagrangeova funkcija:
2. korak Poiščimo parcialne odvode Lagrangeove funkcije in sestavimo sistem enačb iz njihovih enakosti na nič in enačbe veznega pogoja:

Iz prve in druge enačbe izrazimo oz x in l :

Vendar ugotovimo, da zamenjava teh vrednosti spremenljivk v tretjo enačbo sistema ne daje pravilne enakosti. Zato menimo, da je dejansko drugi faktor enakosti enak nič: . Od tu naprej
Iščemo koordinate stacionarnih točk pri vrednosti Lagrangeovega množitelja. Potem iz izrazov za X in Y iz sistema enačb sledi, da . Iz tretje enačbe sistema dobimo.
Pomemben koncept v matematiki je funkcija. Z njegovo pomočjo si lahko vizualno predstavljate številne procese, ki se dogajajo v naravi, in odražate razmerje med določenimi količinami s pomočjo formul, tabel in slik na grafu. Primer je odvisnost tlaka plasti tekočine na telo od globine potopitve, pospešek - od delovanja določene sile na predmet, povečanje temperature - od prenesene energije in številni drugi procesi. Preučevanje funkcije vključuje izgradnjo grafa, ugotavljanje njegovih lastnosti, domene definicije in vrednosti, intervalov naraščanja in padanja. Pomembna točka v ta proces je iskanje ekstremnih točk. Nadalje bomo govorili o tem, kako to storiti pravilno.
O samem konceptu na konkretnem primeru
V medicini nam izris funkcijskega grafa lahko pove o napredovanju bolezni v pacientovem telesu, kar jasno odraža njegovo stanje. Predpostavimo, da os OX predstavlja čas v dnevih, os OU pa temperaturo človeškega telesa. Na sliki je jasno prikazano, kako se ta indikator močno dvigne in nato pade. Prav tako je enostavno opaziti posebne točke, ki odražajo trenutke, ko funkcija, ki je prej naraščala, začne padati in obratno. To so skrajne točke, to je kritične vrednosti (največje in najmanjše) v tem primeru bolnikove temperature, po katerih pride do sprememb v njegovem stanju.

Kot nagiba
Iz slike lahko enostavno ugotovite, kako se spreminja odvod funkcije. Če se ravne črte grafa sčasoma dvignejo, je pozitiven. In bolj ko so strme, večja je vrednost izpeljanke, saj se kot naklona povečuje. V obdobjih padanja ta vrednost prevzame negativne vrednosti in se v točkah ekstrema obrne na nič, graf odvoda pa se v slednjem primeru nariše vzporedno z osjo OX.
Vse druge postopke je treba obravnavati na enak način. Toda najboljši način za povedati o tem konceptu je gibanje različnih teles, ki je jasno prikazano na grafih.
Premikanje
Recimo, da se predmet premika v ravni črti in enakomerno pridobiva hitrost. V tem obdobju se sprememba koordinat telesa grafično prikaže z določeno krivuljo, ki bi jo matematik poimenoval veja parabole. Hkrati se funkcija nenehno povečuje, saj se koordinatni indikatorji vsako sekundo spreminjajo hitreje in hitreje. Graf hitrosti prikazuje obnašanje odvoda, katerega vrednost prav tako narašča. To pomeni, da gibanje nima kritičnih točk.
To bi se nadaljevalo v nedogled. Kaj pa, če se telo nenadoma odloči upočasniti, se ustaviti in se začeti premikati v drugo smer? V tem primeru se bodo kazalniki koordinat začeli zmanjševati. In funkcija bo prešla kritično vrednost in se spremenila iz naraščajočega v padajoče.

S tem primerom lahko ponovno razumete, da se ekstremne točke na grafu funkcije pojavijo v trenutkih, ko ta ni več monotona.
Fizični pomen izpeljanke
Prej opisano je jasno pokazalo, da je odvod v bistvu stopnja spremembe funkcije. To pojasnilo vsebuje svoje fizični pomen. Ekstremne točke so kritična področja na grafu. Lahko jih identificiramo in zaznamo z izračunom vrednosti derivata, ki se izkaže za enako nič.
Obstaja še en znak, ki je zadosten pogoj za ekstrem. Izpeljanka na takšnih prevojnih točkah spremeni predznak: iz "+" v "-" v največjem območju in iz "-" v "+" v minimalnem območju.

Gibanje pod vplivom gravitacije
Predstavljajmo si drugo situacijo. Otroci, ki so se igrali z žogo, so jo metali tako, da se je začela premikati pod kotom proti obzorju. V začetnem trenutku je bila hitrost tega predmeta največja, vendar se je pod vplivom gravitacije začela zmanjševati in z vsako sekundo za enako količino, približno 9,8 m/s 2 . To je vrednost pospeška, ki nastane pod vplivom zemeljske gravitacije med prostim padom. Na Luni bi bil približno šestkrat manjši.
Graf, ki opisuje gibanje telesa, je parabola z vejami, obrnjenimi navzdol. Kako najti skrajne točke? V tem primeru je to vrh funkcije, kjer ima hitrost telesa (žoge) vrednost nič. Odvod funkcije postane nič. V tem primeru se smer in s tem vrednost hitrosti spremenita v nasprotno. Telo vsako sekundo leti hitreje navzdol in za enako pospeši - 9,8 m/s 2 .

Druga izpeljanka
V prejšnjem primeru je graf modula hitrosti narisan kot ravna črta. Ta črta je sprva usmerjena navzdol, saj se vrednost te vrednosti nenehno zmanjšuje. Ko v določenem trenutku dosežejo ničlo, se začnejo kazalniki te vrednosti povečevati in smer grafičnega prikaza modula hitrosti se dramatično spremeni. Črta je zdaj obrnjena navzgor.
Tudi hitrost, ki je odvod koordinate glede na čas, ima kritično točko. V tem območju se funkcija, ki se sprva zmanjšuje, začne povečevati. To je lokacija ekstremne točke odvoda funkcije. V tem primeru naklonski kot tangente postane nič. In pospešek, ki je drugi derivat koordinate glede na čas, spremeni znak iz "-" v "+". In gibanje iz enakomerno počasnega postane enakomerno pospešeno.
Graf pospeška
Zdaj pa poglejmo štiri slike. Vsak od njih prikazuje graf sprememb skozi čas v fizični količini, kot je pospešek. V primeru "A" njegova vrednost ostane pozitivna in konstantna. To pomeni, da se hitrost telesa, tako kot njegova koordinata, nenehno povečuje. Če si predstavljamo, da se bo predmet gibal na ta način neskončno dolgo, se bo izkazalo, da funkcija, ki odraža odvisnost koordinate od časa, nenehno narašča. Iz tega sledi, da nima kritičnih območij. Na grafu odvoda, torej linearno spremenljive hitrosti, ni ekstremnih točk.

Enako velja za primer "B" s pozitivnim in nenehno naraščajočim pospeškom. Res je, da bodo grafi za koordinate in hitrost tukaj nekoliko bolj zapleteni.
Ko gre pospešek na nič
Če pogledamo sliko "B", lahko opazimo popolnoma drugačno sliko, ki označuje gibanje telesa. Njeno hitrost bo grafično predstavila parabola z vejami, usmerjenimi navzdol. Če nadaljujemo vrstico, ki opisuje spremembo pospeška, dokler se ne preseka z osjo OX in še dlje, si lahko predstavljamo, da bo do te kritične vrednosti, kjer se izkaže, da je pospešek enak nič, hitrost predmeta naraščala vse počasneje . Ekstremna točka derivata koordinatne funkcije bo točno na vrhu parabole, po kateri bo telo radikalno spremenilo naravo svojega gibanja in se začelo premikati v drugo smer.
V zadnjem primeru, "G", narave gibanja ni mogoče natančno določiti. Tukaj vemo le, da za neko obravnavano obdobje ni pospeška. To pomeni, da lahko predmet ostane na mestu ali se premika s konstantno hitrostjo.
Problem dodajanja koordinat
Preidimo na naloge, s katerimi se pogosto srečujemo pri študiju algebre v šoli in so ponujene za pripravo na enotni državni izpit. Spodnja slika prikazuje graf funkcije. Potrebno je izračunati vsoto ekstremnih točk.

Naredimo to za ordinatno os tako, da določimo koordinate kritičnih področij, kjer opazimo spremembo značilnosti funkcije. Preprosto povedano, poiskali bomo vrednosti vzdolž osi OX za prevojne točke in nato nadaljevali z dodajanjem nastalih členov. Iz grafa je razvidno, da zavzamejo naslednje vrednosti: -8; -7 ; -5; -3; -2; 1; 3. To sešteje do -21, kar je odgovor.
Optimalna rešitev
Ni treba razlagati, kako pomembno je izvajanje praktične naloge izbiro optimalne rešitve. Navsezadnje obstaja veliko načinov za dosego cilja, vendar je najboljši izhod praviloma le eden. To je izjemno potrebno na primer pri načrtovanju ladij, vesoljskih ladij in letal ter arhitekturnih struktur, da bi našli optimalno obliko teh umetnih predmetov.

Hitrost vozil je v veliki meri odvisna od pravilnega zmanjšanja upora, ki ga doživljajo pri gibanju skozi vodo in zrak, od preobremenitev, ki nastanejo pod vplivom gravitacijskih sil in mnogih drugih kazalcev. Ladja na morju zahteva lastnosti, kot je stabilnost med nevihto, za rečno plovilo pa je pomemben minimalni ugrez. Pri izračunu optimalne zasnove lahko ekstremne točke na grafu jasno podajo idejo najboljša rešitev kompleksen problem. Težave te vrste se pogosto rešujejo v ekonomiji, na poslovnih področjih in v mnogih drugih življenjskih situacijah.
Iz stare zgodovine
Že starodavni modreci so se ukvarjali s skrajnimi problemi. Grški znanstveniki so z matematičnimi izračuni uspešno razvozlali skrivnost površin in prostornin. Bili so prvi, ki so razumeli, da ima na ravnini različnih likov, ki imajo enak obseg, krog vedno največjo ploščino. Podobno ima žoga največjo prostornino med drugimi predmeti v prostoru z enako površino. Takšne znane osebnosti, kot so Arhimed, Evklid, Aristotel, Apolonij, so se posvetile reševanju takšnih problemov. Heron je bil odličen pri iskanju ekstremnih točk in je s pomočjo izračunov zgradil genialne naprave. Ti so vključevali stroje, ki se premikajo s paro, črpalke in turbine, ki delujejo po istem principu.

Gradnja Kartagine
Obstaja legenda, katere zaplet temelji na reševanju enega od ekstremnih problemov. Rezultat poslovnega pristopa feničanske princese, ki se je po pomoč obrnila na modrece, je bila gradnja Kartagine. Zemljišče za to starodavno in slavno mesto je Dido (tako je bilo ime vladarju) podaril vodja enega od afriških plemen. Območje razdelitve se mu sprva ni zdelo zelo veliko, saj naj bi bilo po pogodbi pokrito z volovo kožo. Toda princesa je ukazala svojim vojakom, naj ga narežejo na tanke trakove in iz njih naredijo pas. Izkazalo se je, da je tako dolg, da je pokrival območje, kamor bi lahko stalo celo mesto.
Začetki matematične analize
Zdaj pa se premaknimo iz antičnih časov v poznejšo dobo. Zanimivo je, da je Keplerja k razumevanju osnov matematične analize v 17. stoletju spodbudilo srečanje s prodajalcem vina. Trgovec je bil tako podkovan v svojem poklicu, da je zlahka določil količino pijače v sodu tako, da je vanj spustil železno vrv. Ob razmišljanju o takšni radovednosti je slavni znanstvenik sam rešil to dilemo. Izkazalo se je, da so se spretni sodarji tistega časa naučili izdelovati posode tako, da so imele pri določeni višini in polmeru oboda pritrdilnih obročev največjo zmogljivost.
To je postalo razlog, da je Kepler razmišljal naprej. Sodarji so z dolgotrajnim iskanjem, napakami in novimi poskusi prišli do optimalne rešitve ter prenašali izkušnje iz roda v rod. Toda Kepler je želel pospešiti proces in se z matematičnimi izračuni naučiti, kako narediti isto stvar v kratkem času. Vse njegove dosežke, ki so jih prevzeli njegovi kolegi, so se spremenile v zdaj znana Fermatova in Newton-Leibnizova izreka.
Problem z največjo površino
Predstavljajmo si, da imamo žico, katere dolžina je 50 cm, kako naj iz nje sestavimo pravokotnik z največjo ploščino?
Ko začnete odločati, morate izhajati iz preprostih resnic, ki so znane vsem. Jasno je, da bo obseg naše figure 50 cm, sestavljen je iz dvojne dolžine obeh stranic. To pomeni, da če enega od njih označite kot "X", lahko drugega izrazite kot (25 - X).
Od tu dobimo površino, ki je enaka X(25 - X). Ta izraz si lahko predstavljamo kot funkcijo, ki ima več vrednosti. Rešitev problema zahteva iskanje največjega izmed njih, kar pomeni, da morate najti ekstremne točke.
Da bi to naredili, poiščemo prvi odvod in ga enačimo z nič. Rezultat je preprosta enačba: 25 - 2X = 0.
Iz njega izvemo, da je ena od strani X = 12,5.
Zato drugo: 25 - 12,5 = 12,5.
Izkazalo se je, da bo rešitev problema kvadrat s stranico 12,5 cm.

Kako najti največjo hitrost
Poglejmo še en primer. Predstavljajmo si, da obstaja telo, pravokotno gibanje ki je opisana z enačbo S = - t 3 + 9t 2 - 24t - 8, kjer je prevožena pot izražena v metrih, čas pa v sekundah. Najti moramo največjo hitrost. Kako narediti? Preneseno najdemo hitrost, torej prvo izpeljanko.
Dobimo enačbo: V = - 3t 2 + 18t - 24. Zdaj, da bi rešili problem, moramo spet najti ekstremne točke. To je treba storiti na enak način kot v prejšnji nalogi. Poiščemo prvi odvod hitrosti in ga enačimo z nič.
Dobimo: - 6t + 18 = 0. Zato je t = 3 s. To je čas, ko hitrost telesa prevzame kritično vrednost. Dobljene podatke nadomestimo v enačbo hitrosti in dobimo: V = 3 m/s.
Toda kako razumeti, kaj je to? največja hitrost, ker so lahko kritične točke funkcije njene največje ali najmanjše vrednosti? Če želite preveriti, morate najti drugi odvod hitrosti. Izraža se s številko 6 z znakom minus. To pomeni, da je najdena točka največja. In v primeru pozitivna vrednost drugi derivat bi bil minimum. To pomeni, da se je najdena rešitev izkazala za pravilno.
Navedeni problemi so le del tistih, ki jih je mogoče rešiti, če znaš poiskati ekstremne točke funkcije. Pravzaprav jih je veliko več. In takšno znanje odpira človeški civilizaciji neomejene možnosti.
funkcija y = f(x) se imenuje povečevanje (zmanjševanje) v določenem intervalu, če je za x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).
Če diferenciabilna funkcija y = f (x) narašča (zmanjšuje) na intervalu, potem je njen odvod na tem intervalu f " (x)> 0
(f"(x)< 0).
Pika x O klical lokalna najvišja točka (najmanj) funkcijo f (x), če obstaja okolica točke x o, za vse točke katerih velja neenakost f (x).≤ f (x o ) (f (x )≥ f (x o )).
Pokličejo se največje in najmanjše točke ekstremne točke, in vrednosti funkcije na teh točkah so njene skrajnosti.
Ekstremne točke
Potrebni pogoji ekstrem . Če je točka x O je ekstremna točka funkcije f (x), potem bodisi f " (x o ) = 0 ali f(x o ) ne obstaja. Takšne točke se imenujejo kritično, in sama funkcija je definirana na kritični točki. Ekstreme funkcije je treba iskati med njenimi kritičnimi točkami.
Prvi zadostni pogoj. Pustiti x O - kritična točka. če f" (x ) pri prehodu skozi točko x O spremeni znak plus v minus, nato na piko x o funkcija ima maksimum, sicer ima minimum. Če pri prehodu skozi kritično točko odvod ne spremeni predznaka, potem v točki x O ni ekstrema.
Drugi zadostni pogoj.
Naj ima funkcija f(x).
f" (x ) v bližini točke x
O
in drugi odvod f "" (x 0) v sami točki x o. če f"(x o) = 0, f "" (x 0)>0 (f "" (x 0)<0), то точка x o je lokalna minimalna (maksimalna) točka funkcije f (x). Če je f "" (x 0) = 0, potem morate uporabiti prvi zadostni pogoj ali vključiti višje.
Na segmentu lahko funkcija y = f (x) doseže svojo najmanjšo ali največjo vrednost na kritičnih točkah ali na koncih segmenta.
Primer 3.22.
rešitev. Ker f " (
Problemi iskanja ekstrema funkcije
Primer 3.23. a
rešitev. x in l l
0
≤ x≤
> 0 in kdaj x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funkcije kv.
enote).
Primer 3.24. p ≈
rešitev. p str
S"
R = 2, H = 16/4 = 4.
Primer 3.22.Poiščite ekstreme funkcije f (x) = 2x 3 - 15x 2 + 36x - 14.
rešitev. Ker f " (x ) = 6x 2 - 30x +36 = 6(x -2)(x - 3), potem sta kritični točki funkcije x 1 = 2 in x 2 = 3. Ekstremumi so lahko le v teh točkah. Ker pri prehodu skozi točko x 1 = 2 odvod spremeni predznak iz plusa v minus, ima funkcija na tej točki maksimum. Pri prehodu skozi točko x 2 = 3 odvod spremeni predznak iz minusa v plus, zato ima v točki x 2 = 3 funkcija minimum. Po izračunu vrednosti funkcij v točkah
x 1 = 2 in x 2 = 3, najdemo ekstreme funkcije: največji f (2) = 14 in najmanjši f (3) = 13.
Primer 3.23.V bližini kamnitega zidu je treba zgraditi pravokotno površino, tako da je na treh straneh ograjena z žično mrežo, četrta stran pa meji na zid. Za to obstaja a linearni metri mreže. Pri kakšnem razmerju stranic bo imelo spletno mesto največjo površino?
rešitev.Označimo stranice ploščadi z x in l. Območje mesta je S = xy. Pustiti l- to je dolžina stranice, ki meji na steno. Potem mora biti po pogoju izpolnjena enakost 2x + y = a. Zato je y = a - 2x in S = x (a - 2x), kjer je
0
≤ x≤ a /2 (dolžina in širina območja ne moreta biti negativni). S " = a - 4x, a - 4x = 0 pri x = a/4, od koder je
y = a - 2 × a/4 =a/2. Zaradi x = a /4 je edina kritična točka, preverimo, ali se pri prehodu skozi to točko spremeni predznak odvoda. Pri x a /4 S "> 0 in kdaj x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funkcije S(a/4) = a/4(a - a/2) = a 2 /8 (kv.
enote).
Ker je S zvezen in sta njegovi vrednosti na koncih S(0) in S(a /2) enaki nič, bo najdena vrednost največja vrednost funkcije. Tako je najugodnejše razmerje stranic v danih pogojih problema y = 2x.
Primer 3.24.Potrebna je izdelava zaprtega cilindričnega rezervoarja prostornine V=16 p ≈ 50 m 3. Kakšne naj bodo mere rezervoarja (polmer R in višina H), da bo za njegovo izdelavo porabljeno najmanj materiala?
rešitev.Celotna površina valja je S = 2 str R(R+H). Poznamo prostornino valja V = p R 2 Н Þ Н = V/ p R 2 =16 p / str R2 = 16/R2. Torej je S(R) = 2 str (R 2 +16/R). Najdemo izpeljanko te funkcije:
S"(R) = 2 p (2R- 16/R 2) = 4 p (R- 8/R 2). S" (R) = 0 pri R 3 = 8, torej,
R = 2, H = 16/4 = 4.



