Ekstremne točke funkcije online. Ekstrem funkcije dviju varijabli
Iz ovog članka čitatelj će saznati što je ekstrem funkcionalne vrijednosti, kao io značajkama njegove upotrebe u praktičnim aktivnostima. Proučavanje takvog koncepta iznimno je važno za razumijevanje temelja više matematike. Ova tema je temeljna za dublje proučavanje tečaja.
U kontaktu s
Što je ekstrem?
U školskom tečaju daju se mnoge definicije pojma "ekstremuma". Namjera ovog članka je dati najdublje i najjasnije razumijevanje pojma za one koji ne poznaju ovo pitanje. Dakle, pojam označava koliko funkcionalni jaz poprima minimum ili maksimalna vrijednost na jednom ili drugom skupu.
Ekstrem je istovremeno i minimalna vrijednost funkcije i maksimum. Postoji minimalna točka i maksimalna točka, odnosno ekstremne vrijednosti argumenta na grafu. Glavne znanosti koje koriste ovaj koncept su:
- statistika;
- upravljanje strojem;
- ekonometrija.
Točke ekstrema igraju važnu ulogu u određivanju slijeda dane funkcije. Koordinatni sustav na grafu u u svom najboljem izdanju prikazuje promjenu krajnjeg položaja ovisno o promjeni funkcionalnosti.
Ekstremi derivacije funkcije
Postoji i takav fenomen kao "derivat". Potrebno je odrediti točku ekstrema. Važno je ne brkati minimalne ili maksimalne bodove s najvišim i najnižim vrijednostima. To su različiti koncepti, iako se mogu činiti sličnima.
Vrijednost funkcije je glavni čimbenik u određivanju kako pronaći najveću točku. Derivat se ne formira iz vrijednosti, već isključivo iz njegovog krajnjeg položaja u jednom ili onom poretku.
Sama derivacija se određuje na temelju tih ekstremnih točaka, a ne na temelju najveće ili najmanje vrijednosti. U ruskim školama granica između ova dva pojma nije jasno povučena, što utječe na razumijevanje ove teme općenito.
Razmotrimo sada takav koncept kao "akutni ekstrem". Danas postoji akutna minimalna vrijednost i akutna maksimalna vrijednost. Definicija je dana u skladu s ruskom klasifikacijom kritičnih točaka funkcije. Koncept točke ekstrema osnova je za pronalaženje kritičnih točaka na grafu.

Kako bi definirali takav koncept, oni pribjegavaju korištenju Fermatova teorema. Najvažniji je u proučavanju ekstremnih točaka i daje jasnu ideju o njihovom postojanju u ovom ili onom obliku. Kako bi se osigurala ekstremnost, važno je stvoriti određene uvjete za smanjenje ili povećanje na grafikonu.
Da biste točno odgovorili na pitanje "kako pronaći maksimalnu točku", morate slijediti ove smjernice:
- Pronalaženje točne domene definicije na grafu.
- Traženje derivacije funkcije i točke ekstrema.
- Riješite standardne nejednadžbe za domenu u kojoj se nalazi argument.
- Znati dokazati u kojim je funkcijama točka na grafu definirana i kontinuirana.

Pažnja! Traženje kritične točke funkcije moguće je samo ako postoji derivacija barem drugog reda, što je osigurano visokim udjelom prisutnosti točke ekstrema.
Nužan uvjet za ekstrem funkcije
Da bi postojao ekstrem, važno je da postoje i minimalne i maksimalne točke. Ako se ovo pravilo samo djelomično poštuje, tada je uvjet za postojanje ekstrema povrijeđen.

Svaka se funkcija u bilo kojem položaju mora razlikovati kako bi se identificirala njezina nova značenja. Važno je razumjeti da slučaj točke koja ide prema nuli nije glavni princip za pronalaženje diferencijabilne točke.
Akutni ekstrem, kao i minimum funkcije, iznimno je važan aspekt rješavanja matematičkog problema korištenjem ekstremnih vrijednosti. Kako bismo bolje razumjeli ovu komponentu, važno je obratiti se na tablične vrijednosti za određivanje funkcionalnosti.
| Istraživanje punog smisla | Iscrtavanje grafikona vrijednosti |
| 1. Određivanje točaka rastućih i padajućih vrijednosti. 2. Određivanje točaka diskontinuiteta, ekstrema i sjecišta s koordinatnim osima. 3. Postupak određivanja promjena položaja na grafu. 4. Određivanje indikatora i smjera konveksnosti i konveksnosti, uzimajući u obzir prisutnost asimptota. 5. Izrada sumarne tablice istraživanja sa stajališta određivanja njegovih koordinata. 6. Određivanje intervala porasta i opadanja ekstrema i oštrih točaka. 7. Određivanje konveksnosti i konkavnosti krivulje. 8. Iscrtavanje grafikona uzimajući u obzir istraživanje omogućuje vam da pronađete minimum ili maksimum. |
Glavni element kada je potrebno raditi s ekstremnim točkama je točna konstrukcija njegovog grafikona. Učitelji često ne obraćaju maksimalnu pozornost na tako važan aspekt, što je grubo kršenje obrazovnog procesa. Izgradnja grafikona događa se samo na temelju rezultata proučavanja funkcionalnih podataka, identificiranja akutnih ekstrema, kao i točaka na grafikonu. Oštri ekstremi funkcije derivacije prikazuju se na dijagramu točnih vrijednosti pomoću standardni postupak određivanje asimptota. Točke maksimuma i minimuma funkcije popraćene su s više složene konstrukcije grafička umjetnost. To je zbog dublje potrebe da se proradi problem akutnog ekstremuma. Također je potrebno pronaći derivaciju složene i jednostavne funkcije, jer je to jedan od najvažnijih pojmova u problemu ekstrema. |
Ekstrem funkcionalnog
Da biste pronašli gornju vrijednost, morate se pridržavati sljedećih pravila:
- odrediti nužan uvjet za ekstremni odnos;
- uzeti u obzir dovoljan uvjet ekstremnih točaka na grafikonu;
- provesti proračun akutnog ekstremuma.
Također se koriste pojmovi kao što su slabi minimum i jaki minimum. To se mora uzeti u obzir pri određivanju ekstremuma i njegovom točnom proračunu. Istodobno, akutna funkcionalnost je traženje i stvaranje svih potrebnih uvjeta za rad s grafom funkcije.
Definicija 1. Točku M(x 0 ; y 0) nazivamo točkom maksimuma (minimuma) funkcije z = f(x; y) ako postoji okolina točke M takva da za sve točke (x; y) iz ove susjedstvu vrijedi sljedeća nejednakost:
f(x 0 ; y 0) f(x; y), .
Teorem 1
(nužan uvjet za postojanje ekstrema)
. Ako diferencijabilna funkcija z = f(x; y) dosegne ekstrem u točki M(x 0 ; y 0), tada su njezine parcijalne derivacije prvog reda u toj točki jednake nuli, tj.  ;
;
Točke u kojima su parcijalne derivacije jednake nuli nazivaju se stacionarni ili kritične točke.
Teorem 2 (dovoljan uvjet za postojanje ekstrema)
Neka je funkcija z = f(x; y):
a) definirana u nekoj okolini točke (x 0 ; y 0), u kojoj  I
I  ;
;
b) ima kontinuirane parcijalne izvodnice drugog reda u ovoj točki
 ;
;


Tada, ako je = AC B 2 > 0, tada u točki (x 0 ; y 0) funkcija z = f(x; y) ima ekstrem, a ako je A< 0 (или С < 0) – максимум, если А >0 (ili C > 0) – minimum. U slučaju = AC B 2< 0, функция z = f(x; y) экстремума не имеет. Если = AC B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).
Primjer 1. Odredite ekstremum funkcije z = x 2 + xy + y 2 3x 6y.
Riješenje. Nađimo parcijalne derivacije prvog reda:


Iskoristimo nužan uvjet za postojanje ekstrema:


Rješavanjem sustava jednadžbi nalazimo x i y koordinate stacionarnih točaka: x = 0; y = 3, tj. M(0; 3).
Izračunajmo parcijalne derivacije drugog reda i pronađimo njihove vrijednosti u točki M.
A =  = 2; C =
= 2; C =  = 2;
= 2;
B =  .
.
Sastavimo diskriminantu = AC B 2 = 2 2 1 > 0, A = 2 > 0. Dakle, u točki M(0; 3) zadana funkcija ima minimum. Vrijednost funkcije u ovoj točki je z min = 9.
Pronađite ekstreme funkcija
322. z = x 2 + y 2 + xy 4x 5y 323. z = y 3 x 3 3xy
324. z = x 2 2xy + 4y 3 325. z =  y 2 x + 6y
y 2 x + 6y
326. z = x y (1 x y) 327. z = 2xy 4x 2y
328. z = e x/2 (x + y 2) 329. z = x 3 + 8y 3 6xy + 1
330. z = 3x 2 y x 3 y 4 331. z = 3x + 6y x 2 xy + y 2
Najveća i najmanja vrijednost funkcije dviju varijabli u zatvorenom području
Kako bismo pronašli najveći I najmanje vrijednosti funkcije u zatvorenom području, trebate:
1) pronaći kritične točke koje se nalaze u određenom području i izračunati vrijednosti funkcije u tim točkama;
2) pronaći kritične točke na granici područja i izračunati najveće i najmanje vrijednosti funkcija na njima;
3) od svih pronađenih vrijednosti odaberite najveću i najmanju.
Primjer 2. Pronađite najveću i najmanju vrijednost funkcije z =  u krugu x 2 + y 2 1.
u krugu x 2 + y 2 1.
Riješenje. Nađimo koordinate kritičnih točaka unutar promatranog područja za koje izračunavamo parcijalne derivacije prvog reda funkcije z i izjednačavamo ih s nulom.




odakle je x = 0, y = 0 i, prema tome, M(0; 0) je kritična točka.
Izračunajmo vrijednost funkcije z u točki M(0; 0): z(0; 0) = 2.
Nađimo kritične točke na granici područja - kružnice definirane jednadžbom x 2 + y 2 = 1. Zamjenom y 2 = 1 - x 2 u funkciju z = z(x; y) dobivamo funkciju jedne varijable
z =  ;
;
gdje je x[1; 1].
Izračunavši derivaciju  i izjednačavanjem s nulom dobivamo kritične točke na granici područja x 1 = 0, x 2 =
i izjednačavanjem s nulom dobivamo kritične točke na granici područja x 1 = 0, x 2 =  , x 3 =
, x 3 = 
Nađimo vrijednost funkcije z(x) =  na kritičnim točkama i na krajevima segmenta [1; 1]: z(0) = ;
na kritičnim točkama i na krajevima segmenta [1; 1]: z(0) = ;  =;
=; ; z(1) = ; z(1) =
; z(1) = ; z(1) = 
Izaberimo najveću i najmanju među vrijednostima funkcije z u kritičnim točkama koje se nalaze unutar i na granici kruga.
Dakle, z max. = z(0; 0) = 2
U problemima optimizacije potrebno je pronaći ekstreme funkcije dviju ili više varijabli pod uvjetom da postoji odnos između varijabli ovog odnosa, zadan jednadžbom ![]() . U ovom slučaju kažemo da moramo pronaći uvjetna krajnost
.
. U ovom slučaju kažemo da moramo pronaći uvjetna krajnost
.
Da biste pronašli uvjetni ekstrem, morate pronaći parcijalne derivacije i odlučiti sustavi jednadžbi Postoji algoritam za pronalaženje uvjetnog ekstremuma u tri koraka, koji ćemo sada analizirati na primjeru, te geometrijsko značenje uvjetnog ekstremuma, koje bi svi trebali doprijeti prilikom analize upravo ovog primjera.
Dakle, algoritam ćemo analizirati na primjeru najčešćeg problema - pronalaženje uvjetnog ekstrema funkcije dviju varijabli. .
Korak 1. Predstavljeno Lagrangeova funkcija
gdje je prvi član sama izvorna funkcija, a drugi član s predznakom minus je lijeva strana jednadžbe uvjeta veze, pomnožena s (lambda) - Lagrangeovim množiteljem.
Primjer 1. Pronaći uvjetne krajnosti funkcija dviju varijabli koja izražava površinu pravokutnika u smislu njegovih stranica x I g pod uvjetom da postoji uže koje može vezati ovaj pravokutnik, a duljina tog užeta je 100.
Korak 1. Riješenje. Dovedimo jednadžbu uvjeta veze u traženi oblik s nulom na desnoj strani:
![]() .
.
Sastavljajmo Lagrangeova funkcija:
Korak 2. Od jednakosti sastavljamo sustav jednadžbi parcijalne derivacije nula i jednadžba uvjeta veze (nužni znak postojanja uvjetnog ekstremuma):
Rješenja ovog sustava jednadžbi su točke mogućeg uvjetnog ekstremuma - stacionarne točke ili, kako se još kaže, kritične točke.
Primjer 1. Korak 2.
Riješenje.

x I g :
Zamijenimo ove izraze u treću jednadžbu i pronađimo vrijednost Lagrangeovog množitelja:

x I g i pronađite vrijednosti varijabli izvorne funkcije:

Dobili smo i. Ove vrijednosti su također koordinate stacionarne točke. Tako smo dobili stacionarnu točku.
3. korak Neka je stacionarna točka pronađena u koraku 2. Da biste odredili je li uvjetni ekstrem minimum ili maksimum, trebate pronaći drugi diferencijal Lagrangeove funkcije
![]()
i u rezultirajućem izrazu zamijenite umjesto "lambda" njegove vrijednosti (vrijednosti Lagrangeovog množitelja) pronađene u koraku 2.
Ako je vrijednost drugog diferencijala Lagrangeove funkcije manja od nule (), tada je stacionarna točka točka maksimuma; ako je veća od nule (), tada je stacionarna točka točka minimuma. Ako je vrijednost drugog diferencijala Lagrangeove funkcije jednaka nuli, potrebno je dodatno istraživanje, no takvi se slučajevi praktički ne susreću u zadacima zadanim studentima.
Koordinate stacionarnih točaka zamjenjuju se u početnu točku i tako konačno nalazimo uvjetne krajnosti (ili minimum i maksimum ili jedan od ovih ekstrema).
Primjer 1. Korak 3.
Riješenje. Nađimo drugi diferencijal Lagrangeove funkcije:
![]()
U našem slučaju, budući da su prva i treća komponenta jednake nuli, ne moramo u njih zamijeniti vrijednosti Lagrangeovog množitelja. Ali morate pronaći odnos između razlika dx I dy :
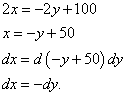
Budući da su dobivene vrijednosti suprotnog predznaka, nalazimo da je u svakom slučaju .
Sada možemo pronaći vrijednost uvjetni ekstrem izvorne funkcije, što je maksimalno:
![]() .
.
Ovo je najveća površina pravokutnika određena izvornom funkcijom, koja se može ograničiti užetom duljine 100.
Primjer 2. Pronaći uvjetne krajnosti
Korak 1. Sastavljajmo Lagrangeova funkcija:
Korak 2. Nađimo parcijalne derivacije Lagrangeove funkcije i sastavimo sustav jednadžbi od njihovih jednakosti na nulu i jednadžbu uvjeta veze:

Iz prve i druge jednadžbe izražavamo redom x I g :

Zamijenimo ove izraze u treću jednadžbu i pronađimo vrijednosti Lagrangeovog množitelja:

Zamijenimo sada vrijednost Lagrangeovog množitelja u izraze za x I g i pronađite vrijednosti varijabli izvorne funkcije za dvije vrijednosti Lagrangeovog množitelja:

Ove x i y vrijednosti su koordinate dviju stacionarnih točaka. Tako smo dobili stacionarne točke ![]() .
.
3. korak Nađimo parcijalne derivacije drugog reda Lagrangeove funkcije:
Nađimo drugi diferencijal Lagrangeove funkcije pomoću formule
![]() :
:
![]()
Dobili smo vrijednost manju od nule, dakle, bod - bod uvjetni maksimum:
![]() .
.
Odredimo predznak drugog diferencijala Lagrangeove funkcije na vrijednost Lagrangeovog množitelja:
![]()
Dobili smo vrijednost veću od nule, dakle, bod - bod uvjetni minimum:
![]() .
.
Tako, uvjetne krajnosti nalaze se zadane funkcije.
Primjer 3. Pronaći uvjetne krajnosti funkcije dviju varijabli podložne .
Korak 1. Sastavljajmo Lagrangeova funkcija:
Korak 2. Nađimo parcijalne derivacije Lagrangeove funkcije i sastavimo sustav jednadžbi od njihovih jednakosti na nulu i jednadžbu uvjeta veze:

Iz prve i druge jednadžbe izražavamo redom x I g :

Smatramo da, međutim, zamjena ovih vrijednosti varijabli u treću jednadžbu sustava ne daje točnu jednakost. Stoga smatramo da je zapravo drugi faktor jednakosti jednak nuli: . Odavde dobivamo
Tražimo koordinate stacionarnih točaka na vrijednosti Lagrangeovog množitelja. Tada iz izraza za X i Y iz sustava jednadžbi slijedi da je . Iz treće jednadžbe sustava dobivamo.
Važan pojam u matematici je funkcija. Uz njegovu pomoć možete vizualno zamisliti mnoge procese koji se odvijaju u prirodi i odražavati odnos između određenih količina pomoću formula, tablica i slika na grafikonu. Primjer je ovisnost pritiska sloja tekućine na tijelo o dubini uranjanja, ubrzanje - o djelovanju određene sile na objekt, povećanje temperature - o prenesenoj energiji i mnogi drugi procesi. Proučavanje funkcije uključuje konstruiranje grafa, otkrivanje njegovih svojstava, domene definicije i vrijednosti, intervala porasta i opadanja. Važna točka u ovaj proces je pronaći ekstremne točke. Dalje ćemo razgovarati o tome kako to učiniti ispravno.
O samom pojmu na konkretnom primjeru
U medicini, crtanje grafa funkcije može nam reći o napredovanju bolesti u tijelu pacijenta, jasno odražavajući njegovo stanje. Pretpostavimo da os OX predstavlja vrijeme u danima, a os OU temperaturu ljudskog tijela. Slika jasno pokazuje kako ovaj pokazatelj naglo raste, a zatim pada. Također je lako uočiti posebne točke koje odražavaju trenutke kada funkcija, prethodno rastuća, počinje opadati, i obrnuto. To su ekstremne točke, odnosno kritične vrijednosti (maksimalne i minimalne) u ovom slučaju pacijentove temperature, nakon kojih dolazi do promjena u njegovom stanju.

Kut nagiba
Sa slike lako možete odrediti kako se mijenja derivacija funkcije. Ako ravne linije grafikona idu gore tijekom vremena, tada je pozitivan. I što su strmije, to je veća vrijednost derivata, jer se kut nagiba povećava. U razdobljima pada ova vrijednost poprima negativne vrijednosti, pretvarajući se u nulu u točkama ekstrema, a grafikon derivacije u potonjem slučaju crta se paralelno s osi OX.
Svaki drugi proces treba tretirati na isti način. Ali najbolji način da kažete o ovom konceptu je kretanje različitih tijela, jasno prikazano na grafikonima.
Pokret
Pretpostavimo da se objekt kreće ravnomjerno, ravnomjerno povećavajući brzinu. U tom razdoblju promjena koordinata tijela grafički se prikazuje određenom krivuljom, koju bi matematičar nazvao granom parabole. Istodobno, funkcija se stalno povećava, budući da se koordinatni indikatori mijenjaju sve brže i brže svake sekunde. Grafikon brzine pokazuje ponašanje derivacije čija vrijednost također raste. To znači da kretanje nema kritičnih točaka.
Ovo bi se nastavilo unedogled. Ali što ako tijelo odjednom odluči usporiti, stati i početi se kretati u drugom smjeru? U tom će se slučaju indikatori koordinata početi smanjivati. I funkcija će proći kritičnu vrijednost i okrenuti se od rastućeg ka opadajućem.

Koristeći ovaj primjer, opet možete shvatiti da se točke ekstrema na grafu funkcije pojavljuju u trenucima kada ona prestane biti monotona.
Fizičko značenje izvedenice
Ono što je ranije opisano jasno je pokazalo da je derivacija u biti brzina promjene funkcije. Ovo pojašnjenje sadrži svoje fizičko značenje. Točke ekstrema su kritična područja na grafikonu. Oni se mogu identificirati i detektirati izračunavanjem vrijednosti derivacije, koja se ispostavlja jednakom nuli.
Postoji još jedan znak koji je dovoljan uvjet za ekstrem. Izvodnica u takvim točkama infleksije mijenja predznak: od “+” do “-” u maksimalnom području i od “-” do “+” u minimalnom području.

Kretanje pod utjecajem gravitacije
Zamislimo drugu situaciju. Djeca su je, igrajući se loptom, bacala tako da se počela kretati pod kutom prema horizontu. U početnom trenutku brzina ovog objekta bila je najveća, ali je pod utjecajem gravitacije počela opadati, i to sa svakom sekundom za isto toliko, jednako otprilike 9,8 m/s 2 . To je vrijednost akceleracije koja nastaje pod utjecajem zemljine teže tijekom slobodnog pada. Na Mjesecu bi bio oko šest puta manji.
Graf koji opisuje kretanje tijela je parabola s granama usmjerenim prema dolje. Kako pronaći ekstremne točke? U ovom slučaju to je vrh funkcije, gdje brzina tijela (lopte) poprima nultu vrijednost. Derivacija funkcije postaje nula. U tom se slučaju smjer, a time i vrijednost brzine, mijenja u suprotno. Tijelo svake sekunde sve brže leti prema dolje, a jednako se i ubrzava - 9,8 m/s 2 .

Druga derivacija
U prethodnom slučaju, graf modula brzine nacrtan je kao ravna linija. Ova linija je u početku usmjerena prema dolje, jer se vrijednost ove vrijednosti stalno smanjuje. Dostigavši nulu u jednom trenutku, tada se pokazatelji ove vrijednosti počinju povećavati, a smjer grafičkog prikaza modula brzine dramatično se mijenja. Linija je sada usmjerena prema gore.
Brzina, budući da je derivacija koordinate u odnosu na vrijeme, također ima kritičnu točku. U ovom području, funkcija, koja se u početku smanjuje, počinje rasti. Ovo je mjesto ekstremne točke derivacije funkcije. U tom slučaju kut nagiba tangente postaje nula. A ubrzanje, kao druga derivacija koordinate u odnosu na vrijeme, mijenja predznak iz “-” u “+”. I kretanje od jednoliko sporog postaje jednoliko ubrzano.
Grafikon ubrzanja
Sada pogledajmo četiri slike. Svaki od njih prikazuje grafikon promjena tijekom vremena u fizičkoj veličini kao što je ubrzanje. U slučaju "A" njegova vrijednost ostaje pozitivna i konstantna. To znači da se brzina tijela, kao i njegova koordinata, stalno povećava. Ako zamislimo da će se objekt kretati na ovaj način beskonačno dugo vremena, funkcija koja odražava ovisnost koordinate o vremenu će se pokazati stalno rastućom. Iz toga proizlazi da nema kritičnih područja. Na grafu derivacije, odnosno linearno promjenjive brzine, također nema točaka ekstrema.

Isto vrijedi i za slučaj "B" s pozitivnim i stalno rastućim ubrzanjem. Istina, grafikoni za koordinate i brzinu ovdje će biti nešto složeniji.
Kada ubrzanje ide na nulu
Gledajući sliku "B", može se uočiti potpuno drugačija slika koja karakterizira kretanje tijela. Njezinu brzinu grafički ćemo prikazati parabolom s granama usmjerenim prema dolje. Ako nastavimo liniju koja opisuje promjenu akceleracije sve dok se ne siječe s osi OX i dalje, možemo zamisliti da će do te kritične vrijednosti, gdje se akceleracija ispostavlja da je nula, brzina objekta rasti sve sporije . Ekstremna točka derivata koordinatne funkcije bit će točno na vrhu parabole, nakon čega će tijelo radikalno promijeniti prirodu svog kretanja i početi se kretati u drugom smjeru.
U posljednjem slučaju, "G", priroda kretanja ne može se točno odrediti. Ovdje samo znamo da nema ubrzanja za neko promatrano razdoblje. To znači da objekt može ostati na mjestu ili se kretati konstantnom brzinom.
Problem zbrajanja koordinata
Prijeđimo na zadatke koji se često susreću pri proučavanju algebre u školi i nude se za pripremu za Jedinstveni državni ispit. Slika ispod prikazuje graf funkcije. Potrebno je izračunati zbroj točaka ekstrema.

Učinimo to za ordinatnu os određivanjem koordinata kritičnih područja u kojima se opaža promjena karakteristika funkcije. Jednostavno rečeno, pronaći ćemo vrijednosti duž OX osi za točke infleksije, a zatim nastaviti s dodavanjem rezultirajućih članova. Prema grafikonu vidljivo je da poprimaju sljedeće vrijednosti: -8; -7 ; -5; -3; -2; 1; 3. To daje zbroj -21, što je odgovor.
Optimalno rješenje
Nema potrebe objašnjavati koliko je važno provesti praktičnih zadataka izbor optimalnog rješenja. Uostalom, postoji mnogo načina za postizanje cilja, ali najbolji izlaz, u pravilu, je samo jedan. To je iznimno potrebno, primjerice, kod projektiranja brodova, svemirskih brodova i zrakoplova te arhitektonskih građevina kako bi se pronašao optimalan oblik ovih objekata koje je napravio čovjek.

Brzina vozila uvelike ovisi o pravilnom minimiziranju otpora koji doživljavaju pri kretanju kroz vodu i zrak, o preopterećenjima koja nastaju pod utjecajem gravitacijskih sila i mnogim drugim pokazateljima. Brod na moru zahtijeva takve osobine kao što je stabilnost tijekom oluje; za riječni brod važan je minimalni gaz. Prilikom izračuna optimalnog dizajna, točke ekstrema na grafikonu mogu jasno dati ideju o tome najbolje rješenje složen problem. Problemi ove vrste često se rješavaju u ekonomiji, u poslovnim područjima iu mnogim drugim životnim situacijama.
Iz davne povijesti
Čak su i stari mudraci bili zaokupljeni ekstremnim problemima. Grčki su znanstvenici matematičkim izračunima uspješno razotkrili misterij površina i volumena. Oni su prvi shvatili da na ravnini raznih likova koji imaju isti obim, krug uvijek ima najveću površinu. Slično tome, lopta je obdarena najvećim volumenom među ostalim objektima u prostoru s istom površinom. Takve poznate ličnosti poput Arhimeda, Euklida, Aristotela, Apolonija posvetile su se rješavanju takvih problema. Heron je bio izvrstan u pronalaženju točaka ekstrema te je pomoću proračuna napravio genijalne naprave. To uključuje strojeve koji se pokreću parom, pumpe i turbine koje rade na istom principu.

Izgradnja Kartage
Postoji legenda čija se radnja temelji na rješavanju jednog od ekstremnih problema. Rezultat poslovnog pristupa feničke princeze, koja se za pomoć obratila mudracima, bila je izgradnja Kartage. Parcelu za ovaj drevni i slavni grad Didonu (tako se zvao vladar) dao je vođa jednog od afričkih plemena. Područje parcele u početku mu se nije činilo velikim, jer je prema ugovoru trebalo biti prekriveno volovskom kožom. Ali princeza je naredila svojim vojnicima da ga izrežu na tanke trake i od njih naprave pojas. Ispostavilo se da je toliko dugačka da je pokrivala područje na koje bi mogao stati cijeli grad.
Porijeklo matematičke analize
Prijeđimo sada iz antičkih vremena u kasniju eru. Zanimljivo je da je Keplera na razumijevanje temelja matematičke analize u 17. stoljeću potaknuo susret s prodavačem vina. Trgovac je bio toliko upućen u svoju struku da je lako mogao odrediti količinu pića u bačvi jednostavnim spuštanjem željeznog užeta u nju. Osvrćući se na takav kuriozitet, slavni je znanstvenik za sebe uspio riješiti i ovu dilemu. Ispostavilo se da su vješti bačvari toga doba umijeli izrađivati posude tako da su, na određenoj visini i polumjeru opsega karika za pričvršćivanje, imale maksimalan kapacitet.
To je Kepleru bio razlog za daljnje razmišljanje. Dugom potragom, pogreškama i novim pokušajima bačvari su došli do optimalnog rješenja, prenoseći svoje iskustvo s koljena na koljeno. No, Kepler je želio ubrzati proces i matematičkim izračunima naučiti kako napraviti istu stvar u kratkom vremenu. Svi njegovi razvoji, koje su prihvatili njegovi kolege, pretvorili su se u danas poznate Fermatove i Newton-Leibnizove teoreme.
Problem s maksimalnom površinom
Zamislimo da imamo žicu duljine 50 cm.Kako od nje sastaviti pravokutnik koji ima najveću površinu?
Kada odlučujete, trebali biste poći od jednostavnih istina koje su svima poznate. Jasno je da će opseg naše figure biti 50 cm, a sastoji se od dvostrukih duljina obje strane. To znači da, nakon što je jedan od njih označen kao "X", drugi se može izraziti kao (25 - X).
Odavde dobivamo površinu jednaku X(25 - X). Ovaj izraz se može smatrati funkcijom koja ima više vrijednosti. Rješavanje problema zahtijeva pronalaženje njihovog maksimuma, što znači da morate pronaći točke ekstrema.
Da bismo to učinili, pronalazimo prvu derivaciju i izjednačavamo je s nulom. Rezultat je jednostavna jednadžba: 25 - 2X = 0.
Iz njega saznajemo da je jedna od stranica X = 12,5.
Prema tome, drugi: 25 - 12,5 = 12,5.
Ispada da će rješenje problema biti kvadrat sa stranom od 12,5 cm.

Kako pronaći maksimalnu brzinu
Pogledajmo još jedan primjer. Zamislimo da postoji tijelo, pravocrtno kretanje koja je opisana jednadžbom S = - t 3 + 9t 2 - 24t - 8, gdje je prijeđeni put izražen u metrima, a vrijeme u sekundama. Moramo pronaći maksimalnu brzinu. Kako to učiniti? Preuzeto nalazimo brzinu, odnosno prvu derivaciju.
Dobivamo jednadžbu: V = - 3t 2 + 18t - 24. Sada, da bismo riješili problem, opet moramo pronaći točke ekstrema. To se mora učiniti na isti način kao u prethodnom zadatku. Nađemo prvu derivaciju brzine i izjednačimo je s nulom.
Dobivamo: - 6t + 18 = 0. Odatle je t = 3 s. To je vrijeme kada brzina tijela poprima kritičnu vrijednost. Dobivene podatke zamijenimo u jednadžbu brzine i dobijemo: V = 3 m/s.
Ali kako razumjeti što je to? maksimalna brzina, jer kritične točke funkcije mogu biti njezine najveće ili najmanje vrijednosti? Za provjeru je potrebno pronaći drugu derivaciju brzine. Izražava se brojem 6 s predznakom minus. To znači da je pronađena točka maksimum. I u slučaju pozitivna vrijednost drugi bi izvod bio minimum. To znači da se pronađeno rješenje pokazalo točnim.
Zadaci navedeni kao primjer samo su dio onih koji se mogu riješiti ako znate pronaći točke ekstrema funkcije. Zapravo, ima ih mnogo više. A takvo znanje otvara neograničene mogućnosti za ljudsku civilizaciju.
Funkcija y = f(x) zove se povećavajući se (smanjujući se) u određenom intervalu, ako je za x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).
Ako diferencijabilna funkcija y = f (x) raste (opada) na intervalu, tada je njezina derivacija na tom intervalu f " (x)> 0
(f"(x)< 0).
Točka x O nazvao lokalna maksimalna točka (minimum) funkcija f (x) ako postoji okolina točke x o, za sve točke za koje vrijedi nejednakost f (x).≤ f (x o ) (f (x )≥ f (x o )).
Pozivaju se maksimalne i minimalne točke ekstremne točke, a vrijednosti funkcije u tim točkama su njezine krajnosti.
Ekstremne točke
Potrebni uvjeti ekstremno . Ako je točka x O je točka ekstrema funkcije f (x), tada ili f " (x o ) = 0, ili f(x o ) ne postoji. Takve se točke nazivaju kritično, a sama funkcija je definirana u kritičnoj točki. Ekstreme funkcije treba tražiti među njezinim kritičnim točkama.
Prvi dovoljan uvjet. Neka x O - kritična točka. Ako f" (x ) pri prolasku kroz točku x O mijenja znak plus u minus, a zatim na točku x o funkcija ima maksimum, inače ima minimum. Ako pri prolasku kroz kritičnu točku derivacija ne promijeni predznak, tada u točki x O nema ekstrema.
Drugi dovoljan uvjet.
Neka funkcija f(x) ima
f" (x ) u blizini točke x
O
a druga derivacija f "" (x 0) u samoj točki x o. Ako f"(x o) = 0, f "" (x 0)>0 (f "" (x 0)<0), то точка x o je lokalna točka minimuma (maksimuma) funkcije f (x). Ako je f "" (x 0) = 0, tada morate ili upotrijebiti prvi dovoljan uvjet ili uključiti više.
Na segmentu funkcija y = f (x) može doseći svoju minimalnu ili maksimalnu vrijednost bilo u kritičnim točkama ili na krajevima segmenta.
Primjer 3.22.
Riješenje. Jer f " (
Problemi nalaženja ekstrema funkcije
Primjer 3.23. a
Riješenje. x I g g
0
≤ x≤
> 0, i kada x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funkcije kv.
jedinice).
Primjer 3.24. p ≈
Riješenje. p str
S"
R = 2, H = 16/4 = 4.
Primjer 3.22.Nađite ekstreme funkcije f (x) = 2x 3 - 15x 2 + 36x - 14.
Riješenje. Jer f " (x ) = 6x 2 - 30x +36 = 6(x -2)(x - 3), tada su kritične točke funkcije x 1 = 2 i x 2 = 3. Ekstremumi mogu biti samo u tim točkama. Kako pri prolasku kroz točku x 1 = 2 derivacija mijenja predznak iz plusa u minus, tada funkcija u ovoj točki ima maksimum. Prolaskom kroz točku x 2 = 3 derivacija mijenja predznak iz minusa u plus, pa u točki x 2 = 3 funkcija ima minimum. Izračunavši vrijednosti funkcije u točkama
x 1 = 2 i x 2 = 3, nalazimo ekstreme funkcije: maksimum f (2) = 14 i minimum f (3) = 13.
Primjer 3.23.U blizini kamenog zida potrebno je izgraditi pravokutni prostor tako da je sa tri strane ograđen žičanom mrežom, a četvrta strana je uz zid. Za ovo postoji a dužni metri mreže. U kojem će omjeru stranica imati najveću površinu?
Riješenje.Označimo stranice platforme sa x I g. Površina mjesta je S = xy. Neka g- ovo je duljina stranice uz zid. Tada prema uvjetu mora biti zadovoljena jednakost 2x + y = a. Stoga je y = a - 2x i S = x (a - 2x), gdje je
0
≤ x≤ a /2 (duljina i širina područja ne mogu biti negativne). S " = a - 4x, a - 4x = 0 pri x = a/4, odakle
y = a - 2 × a/4 = a/2. Jer x = a /4 je jedina kritična točka; provjerimo mijenja li se predznak derivacije prolaskom kroz tu točku. Na x a /4 S "> 0, i kada x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funkcije S(a/4) = a/4(a - a/2) = a 2 /8 (kv.
jedinice).
Budući da je S kontinuirano uključen i da su njegove vrijednosti na krajevima S(0) i S(a /2) jednake nuli, tada će pronađena vrijednost biti najveća vrijednost funkcije. Dakle, najpovoljniji omjer stranica u danim uvjetima problema je y = 2x.
Primjer 3.24.Potrebno je izraditi zatvoreni cilindrični spremnik kapaciteta V=16 p ≈ 50 m 3. Kolike bi trebale biti dimenzije spremnika (polumjer R i visina H) da se za njegovu izradu potroši što manje materijala?
Riješenje.Ukupna površina cilindra je S = 2 str R(R+H). Poznata nam je zapremina cilindra V = p R 2 N Þ N = V/ p R 2 =16 p / str R2 = 16/R2. Dakle, S(R) = 2 str (R 2 +16/R). Nalazimo izvod ove funkcije:
S"(R) = 2 p (2R- 16/R 2) = 4 p (R- 8/R 2). S" (R) = 0 kod R 3 = 8, dakle,
R = 2, H = 16/4 = 4.



