Çevrimiçi bir fonksiyonun ekstremum noktaları. İki değişkenli bir fonksiyonun ekstremumu

Bu makaleden okuyucu, aşırı işlevsel değerin ne olduğunu ve pratik faaliyetlerde kullanımının özelliklerini öğrenecektir. Böyle bir kavramı incelemek, yüksek matematiğin temellerini anlamak için son derece önemlidir. Bu konu, dersin daha derinlemesine incelenmesi için temeldir.

Temas halinde

Ekstremum nedir?

Okul derslerinde “ekstremum” kavramına ilişkin pek çok tanım verilmektedir. Bu makale, konuyu bilmeyenler için terimin en derin ve en net anlayışını vermeyi amaçlamaktadır. Dolayısıyla terim, fonksiyonel boşluğun ne kadar minimum veya maksimum değerşu ya da bu sette.

Bir ekstremum, bir fonksiyonun hem minimum hem de maksimum değeridir. Grafikte argümanın minimum noktası ve maksimum noktası yani uç değerleri vardır. Bu kavramı kullanan başlıca bilimler şunlardır:

• İstatistik;
• makine kontrolü;
• Ekonometri.

Ekstrem noktalar belirli bir fonksiyonun sırasını belirlemede önemli bir rol oynar. Grafikteki koordinat sistemi en iyi haliyle işlevsellikteki değişikliğe bağlı olarak uç konumdaki değişikliği gösterir.

Türev fonksiyonunun ekstremumları

Bir de “türev” diye bir olgu var. Ekstrem noktayı belirlemek gerekir. Minimum veya maksimum noktaları en yüksek ve en düşük değerlerle karıştırmamak önemlidir. Bunlar benzer gibi görünse de farklı kavramlardır.

Fonksiyonun değeri maksimum noktanın nasıl bulunacağını belirleyen ana faktördür. Türev değerlerden değil, yalnızca şu veya bu sıradaki aşırı konumundan oluşur.

Türevin kendisi, en büyük veya en küçük değere göre değil, bu uç noktalara göre belirlenir. Rus okullarında bu iki kavram arasındaki çizginin net bir şekilde çizilmemesi bu konunun genel olarak anlaşılmasını etkilemektedir.

Şimdi “akut ekstremum” gibi bir kavramı ele alalım. Günümüzde bir akut minimum değer, bir de akut maksimum değer bulunmaktadır. Tanım, bir fonksiyonun kritik noktalarının Rusya sınıflandırmasına uygun olarak verilmiştir. Ekstrem nokta kavramı, bir grafikte kritik noktaları bulmanın temelini oluşturur.

Böyle bir kavramı tanımlamak için Fermat teoremini kullanmaya başvuruyorlar. Uç noktaların incelenmesinde en önemlisidir ve bunların şu ya da bu şekilde varlığına dair net bir fikir verir. Ekstremiteliği sağlamak için grafikte düşüş veya artışa yönelik belirli koşulların yaratılması önemlidir.

"Maksimum nokta nasıl bulunur" sorusuna doğru cevap vermek için şu yönergeleri izlemelisiniz:

1. Grafikte tanımın tam alanını bulma.
2. Bir fonksiyonun türevini ve ekstrem noktasını arayın.
3. Argümanın bulunduğu alan için standart eşitsizlikleri çözün.
4. Grafik üzerinde bir noktanın hangi fonksiyonlarda tanımlı ve sürekli olduğunu ispatlayabilme.

Dikkat! Bir fonksiyonun kritik noktasının aranması, yalnızca en az ikinci dereceden bir türevin olması durumunda mümkündür; bu, yüksek oranda bir ekstremum noktasının varlığıyla sağlanır.

Bir fonksiyonun ekstremumu için gerekli koşul

Bir ekstremun var olabilmesi için hem minimum hem de maksimum noktaların olması önemlidir. Bu kurala yalnızca kısmen uyulursa, bir ekstremun varlığı koşulu ihlal edilir.

Herhangi bir konumdaki her işlevin, yeni anlamlarını tanımlayabilmek için farklılaştırılması gerekir. Bir noktanın sıfıra gitmesi durumunun türevlenebilir bir nokta bulmanın ana ilkesi olmadığını anlamak önemlidir.

Akut ekstremum ve bir fonksiyonun minimumu, ekstrem değerleri kullanarak bir matematik problemini çözmenin son derece önemli bir yönüdür. Bu bileşenin daha iyi anlaşılabilmesi için işlevselliğin belirtilmesi amacıyla tablo değerlerine başvurulması önemlidir.

Tam Anlam Araştırması

Değer Grafiği Çizmek

1. Artan ve azalan değer noktalarının belirlenmesi. 2. Koordinat eksenleri ile süreksizlik noktalarının, ekstremumların ve kesişimlerin bulunması. 3. Bir grafik üzerindeki konum değişikliklerini belirleme süreci. 4. Asimptotların varlığı dikkate alınarak dışbükeylik ve dışbükeylik göstergesinin ve yönünün belirlenmesi. 5. Koordinatlarının belirlenmesi açısından araştırma özet tablosunun oluşturulması. 6. Ekstrem ve keskin noktaların artan ve azalan aralıklarını bulma. 7. Bir eğrinin dışbükeylik ve içbükeyliğinin belirlenmesi. 8. Araştırmayı dikkate alarak bir grafik çizmek minimum veya maksimumu bulmanızı sağlar.

Uç noktalarla çalışmak gerektiğinde ana unsur, grafiğinin doğru oluşturulmasıdır. Okul öğretmenleri, eğitim sürecinin ağır bir ihlali olan bu kadar önemli bir hususa çoğu zaman azami dikkat göstermezler. Bir grafiğin oluşturulması yalnızca fonksiyonel verilerin incelenmesi, akut ekstremlerin belirlenmesi ve grafikteki noktaların sonuçlarına dayanarak gerçekleşir. Türev fonksiyonunun keskin ekstremumları, tam değerlerin grafiği üzerinde şu şekilde görüntülenir: standart prosedür asimptotların belirlenmesi. Fonksiyonun maksimum ve minimum noktalarına daha fazlası eşlik eder karmaşık yapılar grafik Sanatları. Bunun nedeni, akut ekstremum sorununu çözmeye yönelik daha derin bir ihtiyaçtır. Ekstremum problemindeki en önemli kavramlardan biri olduğundan karmaşık ve basit bir fonksiyonun türevini bulmak da gereklidir.

Fonksiyonelin ekstremumu

Yukarıdaki değeri bulmak için aşağıdaki kurallara uymanız gerekir:

• ekstrem bir ilişki için gerekli koşulu belirlemek;
• grafikteki uç noktaların yeterli durumunu dikkate alın;
• Akut ekstremum hesaplamasını yapar.

Zayıf minimum, güçlü minimum gibi kavramlar da kullanılmaktadır. Ekstremumu belirlerken ve doğru hesaplamasını yaparken bu dikkate alınmalıdır. Aynı zamanda akut işlevsellik, bir fonksiyonun grafiğiyle çalışmak için gerekli tüm koşulların aranması ve oluşturulmasıdır.

Tanım 1. M noktasının bundan sonraki tüm (x; y) noktaları için bir komşuluğu varsa, M(x 0 ; y 0) noktasına z = f(x; y) fonksiyonunun maksimum (minimum) noktası denir. mahallede aşağıdaki eşitsizlik geçerlidir:

f(x 0 ; y 0)  f(x; y), .

Teorem 1 (bir ekstremun varlığı için gerekli bir koşul) . Türevlenebilir bir z = f(x; y) fonksiyonu M(x 0; y 0) noktasında bir uç noktaya ulaşırsa, bu durumda onun bu noktadaki birinci dereceden kısmi türevleri sıfıra eşittir;
;

Kısmi türevlerin sıfıra eşit olduğu noktalara denir. sabit veya kritik noktalar.

Teorem 2 (bir ekstremumun varlığı için yeterli koşul)

z = f(x; y) fonksiyonu olsun:

a) (x 0 ; y 0) noktasının belirli bir komşuluğunda tanımlanmış olup, burada
Ve
;

b) bu ​​noktada ikinci dereceden sürekli kısmi türevleri vardır

;

O halde, eğer  = AC  B 2 > 0 ise, (x 0 ; y 0) noktasında z = f(x; y) fonksiyonunun bir ekstremumu vardır ve eğer A< 0 (или С < 0) – максимум, если А >0 (veya C > 0) – minimum.  = AC  B 2 durumunda< 0, функция z = f(x; y) экстремума не имеет. Если  = AC  B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).

Örnek 1. z = x 2 + xy + y 2  3x  6y fonksiyonunun ekstremumunu bulun.

Çözüm. Birinci dereceden kısmi türevleri bulalım:

Bir ekstremun varlığı için gerekli koşulu kullanalım:

Denklem sistemini çözerek sabit noktaların x ve y koordinatlarını buluruz: x = 0; y = 3, yani M(0; 3).

İkinci dereceden kısmi türevleri hesaplayalım ve M noktasındaki değerlerini bulalım.

bir =
= 2; C =
= 2;

B =
.

Diskriminantı oluşturalım  = AC  B 2 = 2  2  1 > 0, A = 2 > 0. Dolayısıyla M(0; 3) noktasında verilen fonksiyonun minimumu vardır. Fonksiyonun bu noktadaki değeri z min = 9'dur.

Fonksiyonların ekstremumlarını bulun

322. z = x 2 + y 2 + xy  4x  5y 323. z = y 3  x 3  3xy

324. z = x 2  2xy + 4y 3 325. z =
 y 2  x + 6y

326. z = x y (1  x  y) 327. z = 2xy  4x  2y

328. z = e  x/2 (x + y 2) 329. z = x 3 + 8y 3  6xy + 1

330. z = 3x 2 y  x 3  y 4 331. z = 3x + 6y  x 2  xy + y 2

Kapalı bir alanda iki değişkenli bir fonksiyonun en büyük ve en küçük değerleri

Bulmak için En büyük Ve en az Kapalı bir bölgedeki bir fonksiyonun değerleri için yapmanız gerekenler:

1) belirli bir alanda bulunan kritik noktaları bulun ve bu noktalardaki fonksiyon değerlerini hesaplayın;

2) bölgenin sınırındaki kritik noktaları bulun ve bu noktalardaki fonksiyonların en büyük ve en küçük değerlerini hesaplayın;

3) bulunan tüm değerlerden en büyüğünü ve en küçüğünü seçin.

Örnek 2. z = fonksiyonunun en büyük ve en küçük değerlerini bulun
x 2 + y 2  1 çemberinde.

Çözüm. z fonksiyonunun birinci dereceden kısmi türevlerini hesapladığımız ve sıfıra eşitlediğimiz, söz konusu bölgenin içinde yer alan kritik noktaların koordinatlarını bulalım.

dolayısıyla x = 0, y = 0 ve dolayısıyla M(0; 0) kritik bir noktadır.

Z fonksiyonunun M(0; 0) noktasındaki değerini hesaplayalım: z(0; 0) = 2.

x 2 + y 2 = 1 denklemiyle tanımlanan bir daire olan bölgenin sınırındaki kritik noktaları bulalım. z = z(x; y) fonksiyonunda y 2 = 1 - x 2'yi değiştirerek bir fonksiyon elde ederiz. bir değişkenin

z =
;

burada x[1; 1].

Türevi hesapladıktan sonra
ve bunu sıfıra eşitleyerek x 1 = 0, x 2 = bölgesinin sınırında kritik noktalar elde ederiz. ,x3 =

z(x) = fonksiyonunun değerini bulalım.
kritik noktalarda ve segmentin uçlarında [1; 1]: z(0) = ;
=;
; z(1) = ; z(1) =

Çemberin içinde ve sınırında yer alan kritik noktalarda z fonksiyonunun değerleri arasından en büyüğünü ve en küçüğünü seçelim.

Yani z maks. = z(0; 0) = 2

Optimizasyon problemlerinde ekstremumların bulunmasına ihtiyaç vardır. iki veya daha fazla değişkenli fonksiyonlar denklemle verilen bu ilişkinin değişkenleri arasında bir ilişki olması koşuluyla . Bu durumda bulmamız gerektiğini söylüyoruz. koşullu ekstremum .

Koşullu ekstremumu bulmak için bulmanız gerekir kısmi türevler ve karar ver denklem sistemleriŞimdi bir örnek kullanarak analiz edeceğimiz, üç adımda koşullu bir ekstremum bulma algoritması ve bu örneği analiz ederken herkese ulaşması gereken koşullu bir ekstremun geometrik anlamı vardır.

Bu nedenle, en yaygın problem örneğini kullanarak algoritmayı analiz edeceğiz - iki değişkenli bir fonksiyonun koşullu ekstremumunu bulmak. .

Aşama 1. Tanıtıldı Lagrange işlevi

burada ilk terim orijinal fonksiyonun kendisidir ve eksi işaretli ikinci terim, bağlantı koşulu denkleminin sol tarafının (lambda) - Lagrange çarpanı ile çarpılmasıdır.

Örnek 1. Bulmak koşullu aşırılıklar bir dikdörtgenin alanını kenarlarına göre ifade eden iki değişkenli bir fonksiyon X Ve sen Bu dikdörtgeni sınırlayabilecek bir ip olması ve bu ipin uzunluğunun 100 olması şartıyla.

Aşama 1.Çözüm. Bağlantı koşulu denklemini sağ tarafta sıfır olacak şekilde istenilen forma getirelim:

.

Hadi oluşturalım Lagrange işlevi:

Adım 2. Eşitliklerden bir denklem sistemi oluşturuyoruz kısmi türevler sıfır ve bağlantı koşulunun denklemi (koşullu bir ekstremun varlığının gerekli bir işareti):

Bu denklem sisteminin çözümleri olası bir koşullu ekstremum noktalarıdır - durağan noktalar veya dedikleri gibi kritik noktalar.

Örnek 1. Adım 2.

Çözüm.

X Ve sen :

Bu ifadeleri üçüncü denklemde yerine koyalım ve Lagrange çarpanının değerini bulalım:

X Ve sen ve orijinal fonksiyonun değişkenlerinin değerlerini bulun:

Aldık ve. Bu değerler aynı zamanda durağan noktanın koordinatlarıdır. Böylece durağan bir noktaya ulaştık.

Aşama 3. 2. adımda bulunan durağan nokta olsun. Koşullu ekstremumun minimum mu yoksa maksimum mu olduğunu belirlemek için Lagrange fonksiyonunun ikinci diferansiyelini bulmanız gerekir.

ve ortaya çıkan ifadede “lambda” yerine 2. adımda bulunan değerlerini (Lagrange çarpanının değerleri) değiştirin.

Lagrange fonksiyonunun ikinci diferansiyelinin değeri sıfırdan () küçükse, durağan nokta bir maksimum noktadır; sıfırdan () büyükse, o zaman durağan nokta bir minimum noktadır. Lagrange fonksiyonunun ikinci diferansiyelinin değeri sıfıra eşitse, ek araştırma gerekir, ancak bu tür durumlar pratikte öğrencilere verilen problemlerde karşımıza çıkmaz.

Sabit noktaların koordinatları başlangıç ​​noktasının yerine konulur ve böylece sonunda şunu buluruz: koşullu aşırılıklar (veya minimum ve maksimum veya bu uç noktalardan biri).

Örnek 1. Adım 3.

Çözüm. Lagrange fonksiyonunun ikinci diferansiyelini bulalım:

Bizim durumumuzda birinci ve üçüncü bileşenler sıfıra eşit olduğundan Lagrange çarpanının değerlerini bunların yerine koymamıza gerek yoktur. Ancak farklar arasındaki ilişkiyi bulmanız gerekir. dx Ve ölmek :

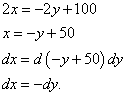
Elde edilen değerler ters işaretli olduğundan her durumda bunu buluyoruz.

Artık değeri bulabiliriz koşullu ekstremum maksimum olan orijinal fonksiyonun değeri:

.

Bu, uzunluğu 100 olan bir ip ile sınırlandırılabilen, orijinal fonksiyon tarafından belirlenen bir dikdörtgenin maksimum alanıdır.

Örnek 2. Bulmak koşullu aşırılıklar

Aşama 1. Hadi oluşturalım Lagrange işlevi:

Adım 2. Lagrange fonksiyonunun kısmi türevlerini bulalım ve bunların eşitliklerinden sıfıra ve bağlantı koşulu denkleminden bir denklem sistemi oluşturalım:

Sırasıyla ifade ettiğimiz birinci ve ikinci denklemlerden X Ve sen :

Bu ifadeleri üçüncü denklemde yerine koyalım ve Lagrange çarpanının değerlerini bulalım:

Şimdi Lagrange çarpanının değerini aşağıdaki ifadelerde yerine koyalım: X Ve sen ve Lagrange çarpanının iki değeri için orijinal fonksiyonun değişkenlerinin değerlerini bulun:

Bu x ve y değerleri iki sabit noktanın koordinatlarıdır. Böylece durağan puanlar elde ettik .

Aşama 3. Lagrange fonksiyonunun ikinci dereceden kısmi türevlerini bulalım:

Aşağıdaki formülü kullanarak Lagrange fonksiyonunun ikinci diferansiyelini bulalım.

:

Sıfırdan küçük bir değer aldık bu nedenle nokta - nokta koşullu maksimum:

.

Lagrange fonksiyonunun ikinci diferansiyelinin işaretini Lagrange çarpanının değerinde belirleyelim:

Sıfırdan büyük bir değer aldık, dolayısıyla nokta - nokta koşullu minimum:

.

Böylece, koşullu aşırılıklar Verilen fonksiyonlar bulunur.

Örnek 3. Bulmak koşullu aşırılıklar iki değişkenli fonksiyonlar.

Aşama 1. Hadi oluşturalım Lagrange işlevi:

Adım 2. Lagrange fonksiyonunun kısmi türevlerini bulalım ve bunların eşitliklerinden sıfıra ve bağlantı koşulu denkleminden bir denklem sistemi oluşturalım:

Sırasıyla ifade ettiğimiz birinci ve ikinci denklemlerden X Ve sen :

Ancak bu değişken değerleri sistemin üçüncü denkleminde yerine koymanın doğru eşitliği sağlamadığını görüyoruz. Bu nedenle eşitliğin ikinci faktörünün aslında sıfıra eşit olduğuna inanıyoruz: . Buradan anlıyoruz

Lagrange çarpanı değerindeki durağan noktaların koordinatlarını arıyoruz. Daha sonra denklem sisteminden X ve Y ifadelerinden şu sonuç çıkar. Sistemin üçüncü denkleminden elde ediyoruz.

Matematikte önemli bir kavram fonksiyondur. Onun yardımıyla, doğada meydana gelen birçok süreci görsel olarak hayal edebilir ve belirli miktarlar arasındaki ilişkiyi formüller, tablolar ve resimler kullanarak bir grafik üzerinde yansıtabilirsiniz. Bir örnek, bir sıvı tabakasının bir cisim üzerindeki basıncının daldırma derinliğine, ivmenin - belirli bir kuvvetin bir nesne üzerindeki etkisine, sıcaklıktaki artışın - aktarılan enerjiye ve diğer birçok sürece bağımlılığıdır. Bir fonksiyonu incelemek, bir grafik oluşturmayı, özelliklerini, tanım alanını ve değerlerini, artış ve azalma aralıklarını bulmayı içerir. Önemli bir nokta bu süreç ekstremum noktaları bulmaktır. Bunun nasıl doğru bir şekilde yapılacağı hakkında daha fazla konuşacağız.

Belirli bir örnek kullanarak konseptin kendisi hakkında

Tıpta, bir fonksiyon grafiğinin çizilmesi, hastanın vücudundaki hastalığın ilerleyişi hakkında bize bilgi verebilir ve durumunu açıkça yansıtabilir. OX ekseninin gün cinsinden zamanı, OU ekseninin ise insan vücut sıcaklığını temsil ettiğini varsayalım. Şekil, bu göstergenin nasıl keskin bir şekilde yükselip sonra düştüğünü açıkça göstermektedir. Daha önce artan bir fonksiyonun azalmaya başladığı veya tam tersi anları yansıtan özel noktaları fark etmek de kolaydır. Bunlar aşırı noktalardır, yani hastanın sıcaklığının bu durumunda kritik değerlerdir (maksimum ve minimum), ardından durumunda değişiklikler meydana gelir.

Eğim açısı

Fonksiyonun türevinin nasıl değiştiğini şekilden kolayca belirleyebilirsiniz. Grafiğin düz çizgileri zamanla yukarı doğru çıkıyorsa bu pozitiftir. Ve eğim açısı arttıkça türevin değeri ne kadar dik olursa o kadar büyük olur. Azalma dönemlerinde bu değer negatif değerler alır, uç noktalarda sıfıra döner ve ikinci durumda türevin grafiği OX eksenine paralel çizilir.

Diğer tüm işlemler aynı şekilde ele alınmalıdır. Ancak bu kavramı anlatmanın en iyi yolu, grafiklerde açıkça gösterilen çeşitli cisimlerin hareketidir.

Hareket

Bir nesnenin düzgün bir şekilde hızlanarak düz bir çizgide hareket ettiğini varsayalım. Bu dönemde vücudun koordinatlarındaki değişiklik, matematikçilerin parabolün dalı olarak adlandıracağı belirli bir eğri ile grafiksel olarak temsil edilir. Aynı zamanda koordinat göstergeleri her saniye daha hızlı değiştiği için fonksiyon sürekli artmaktadır. Hız grafiği, değeri de artan türevin davranışını gösterir. Bu, hareketin kritik noktalarının olmadığı anlamına gelir.

Bu süresiz olarak devam edecekti. Peki ya vücut aniden yavaşlamaya, durmaya ve farklı bir yöne doğru hareket etmeye karar verirse? Bu durumda koordinat göstergeleri azalmaya başlayacaktır. Ve fonksiyon kritik bir değeri geçerek artandan azalan tarafa dönecektir.

Bu örneği kullanarak, bir fonksiyonun grafiğindeki uç noktaların, monotonluğun sona erdiği anlarda ortaya çıktığını bir kez daha anlayabilirsiniz.

Türevin fiziksel anlamı

Daha önce anlatılanlar, türevin aslında fonksiyonun değişim oranı olduğunu açıkça gösterdi. Bu açıklama şunları içerir: fiziksel anlam. Ekstrem noktalar grafikteki kritik alanlardır. Sıfıra eşit olduğu ortaya çıkan türevin değeri hesaplanarak tanımlanabilir ve tespit edilebilirler.

Bir ekstremum için yeterli koşul olan başka bir işaret daha vardır. Bu tür dönüm noktalarındaki türev işaretini maksimum alanda “+”dan “-”ye, minimum alanda “-”den “+”ya değiştirir.

Yer çekimi etkisi altında hareket

Başka bir durum hayal edelim. Topla oynayan çocuklar, topu ufka doğru açılı hareket edecek şekilde fırlattılar. İlk anda, bu nesnenin hızı en yüksekti, ancak yerçekiminin etkisi altında azalmaya başladı ve her saniyede aynı miktarda yaklaşık 9,8 m/s2'ye eşit oldu. Bu, serbest düşüş sırasında yer çekiminin etkisi altında oluşan ivmenin değeridir. Ay'da yaklaşık altı kat daha küçük olurdu.

Bir cismin hareketini tanımlayan grafik, dalları aşağıya bakan bir paraboldür. Ekstrem noktalar nasıl bulunur? Bu durumda cismin (topun) hızının sıfır değerini aldığı fonksiyonun tepe noktasıdır. Fonksiyonun türevi sıfır olur. Bu durumda yön ve dolayısıyla hız değeri ters yönde değişir. Vücut her saniye daha hızlı uçuyor ve aynı miktarda - 9,8 m/s 2 - hızlanıyor.

İkinci türev

Önceki durumda hız modülü grafiği düz bir çizgi olarak çizilmiştir. Bu değerin değeri sürekli azaldığı için bu çizgi başlangıçta aşağıya doğru yönlendirilir. Bir noktada sıfıra ulaştıktan sonra bu değerin göstergeleri artmaya başlar ve hız modülünün grafiksel gösteriminin yönü önemli ölçüde değişir. Çizgi şu anda yukarıyı gösteriyor.

Koordinatın zamana göre türevi olan hızın da kritik bir noktası vardır. Bu bölgede başlangıçta azalan fonksiyon artmaya başlar. Bu, fonksiyonun türevinin uç noktasının konumudur. Bu durumda teğetin eğim açısı sıfır olur. Koordinatın zamana göre ikinci türevi olan ivme ise işareti “-”den “+”ya değiştirir. Ve hareket eşit derecede yavaştan eşit şekilde hızlanmaya başlar.

Hızlanma grafiği

Şimdi dört resme bakalım. Her biri, ivme gibi fiziksel bir nicelikte zaman içindeki değişimlerin bir grafiğini görüntüler. “A” durumunda değeri pozitif ve sabit kalır. Bu, vücudun koordinatları gibi hızının da sürekli arttığı anlamına gelir. Nesnenin sonsuz uzun bir süre bu şekilde hareket edeceğini hayal edersek, koordinatın zamana bağımlılığını yansıtan fonksiyonun sürekli arttığı ortaya çıkacaktır. Buradan kritik alanların olmadığı sonucu çıkıyor. Ayrıca türevin grafiğinde, yani hızın doğrusal olarak değiştiği uç noktalar da yoktur.

Aynı durum pozitif ve sürekli artan ivmeli “B” durumu için de geçerlidir. Doğru, buradaki koordinat ve hız grafikleri biraz daha karmaşık olacak.

İvme sıfıra gittiğinde

“B” şekline bakıldığında vücudun hareketini karakterize eden tamamen farklı bir resim görülebilir. Hızı, dalları aşağı doğru yönlendirilmiş bir parabol ile grafiksel olarak temsil edilecektir. İvme değişimini anlatan çizgiyi OX ekseni ile kesişinceye kadar devam ettirirsek ve daha da ileriye gidersek, ivmenin sıfır olduğu bu kritik değere kadar cismin hızının giderek daha yavaş artacağını hayal edebiliriz. . Koordinat fonksiyonunun türevinin uç noktası tam olarak parabolün tepe noktasında olacaktır, bundan sonra vücut hareketinin doğasını kökten değiştirecek ve farklı bir yönde hareket etmeye başlayacaktır.

Son durumda, “G”, hareketin niteliği kesin olarak belirlenemiyor. Burada sadece söz konusu dönem için herhangi bir ivmelenmenin olmadığını biliyoruz. Bu, nesnenin yerinde kalabileceği veya sabit bir hızla hareket edebileceği anlamına gelir.

Koordinat ekleme problemi

Okulda cebir okurken sıklıkla karşılaşılan ve Birleşik Devlet Sınavına hazırlık için sunulan görevlere geçelim. Aşağıdaki şekil fonksiyonun grafiğini göstermektedir. Ekstrem noktaların toplamını hesaplamak gerekir.

Fonksiyonun özelliklerinde değişiklik gözlemlenen kritik alanların koordinatlarını belirleyerek ordinat ekseni için bunu yapalım. Basitçe söylemek gerekirse, dönüm noktaları için OX ekseni boyunca değerleri bulacağız ve ardından elde edilen terimleri eklemeye devam edeceğiz. Grafiğe göre şu değerleri aldıkları açıktır: -8; -7; -5; -3; -2; 1; 3. Bunun toplamı -21 olur, cevap budur.

En uygun çözüm

Uygulamanın ne kadar önemli olabileceğini açıklamaya gerek yok pratik görevler optimal çözümün seçilmesi. Sonuçta, bir hedefe ulaşmanın birçok yolu vardır, ancak kural olarak en iyi çıkış yolu yalnızca bir tanesidir. Bu, örneğin gemileri, uzay gemilerini, uçakları ve mimari yapıları tasarlarken bu insan yapımı nesnelerin en uygun şeklini bulmak için son derece gereklidir.

Araçların hızı büyük ölçüde su ve havada hareket ederken karşılaştıkları direncin, yerçekimi kuvvetlerinin ve diğer birçok göstergenin etkisi altında ortaya çıkan aşırı yüklerin uygun şekilde en aza indirilmesine bağlıdır. Denizdeki bir gemi, fırtına sırasında stabilite gibi niteliklere ihtiyaç duyar; bir nehir gemisi için minimum su çekimi önemlidir. Optimum tasarımı hesaplarken grafikteki ekstremum noktalar net bir şekilde fikir verebilir. en iyi çözüm karmaşık sorun. Bu tür sorunlar genellikle ekonomide, iş alanlarında ve diğer birçok yaşam durumunda çözülür.

Antik tarihten

Eski bilgeler bile aşırı sorunlarla meşguldü. Yunan bilim adamları matematiksel hesaplamalar yoluyla alanların ve hacimlerin gizemini başarıyla çözdüler. Aynı çevreye sahip çeşitli şekillerden oluşan bir düzlemde dairenin her zaman en büyük alana sahip olduğunu ilk anlayanlar onlardı. Benzer şekilde top, uzaydaki aynı yüzey alanına sahip diğer nesneler arasında maksimum hacme sahiptir. Arşimet, Öklid, Aristoteles, Apollonius gibi ünlü şahsiyetler kendilerini bu tür sorunları çözmeye adadılar. Heron uç noktaları bulmada mükemmeldi ve hesaplamaları kullanarak ustaca cihazlar yaptı. Bunlar arasında buharla hareket eden makineler, pompalar ve aynı prensiple çalışan türbinler yer alıyordu.

Kartaca İnşaatı

Konusu aşırı sorunlardan birinin çözümüne dayanan bir efsane var. Yardım için bilgelere başvuran Fenikeli prensesin gösterdiği iş yaklaşımının sonucu Kartaca'nın inşası oldu. Bu antik ve ünlü şehrin arsası, Afrika kabilelerinden birinin lideri tarafından Dido'ya (hükümdarın adıydı) verildi. Sözleşmeye göre öküz derisiyle kaplanması gerektiğinden, tahsis alanı ilk başta ona çok büyük görünmedi. Ancak prenses askerlerine onu ince şeritler halinde kesip kemer yapmalarını emretti. O kadar uzun olduğu ortaya çıktı ki, bütün bir şehrin sığabileceği bir alanı kaplıyordu.

Matematiksel analizin kökenleri

Şimdi eski zamanlardan daha sonraki bir döneme geçelim. Kepler'in matematiksel analizin temellerini 17. yüzyılda bir şarap satıcısıyla yaptığı toplantıyla anlamaya başlaması ilginçtir. Tüccar mesleğinde o kadar bilgiliydi ki, fıçıdaki içeceğin hacmini, içine demir bir halat indirerek kolayca belirleyebiliyordu. Böyle bir merak üzerine düşünen ünlü bilim adamı, bu ikilemi kendi başına çözmeyi başardı. O zamanların yetenekli fıçıcılarının, sabitleme halkalarının çevresinin belirli bir yüksekliğinde ve yarıçapında maksimum kapasiteye sahip olacak şekilde kap yapma becerisine sahip oldukları ortaya çıktı.

Bu Kepler'in daha fazla düşünmesine neden oldu. Cooper'lar uzun araştırmalar, hatalar ve yeni denemeler sonucunda en uygun çözüme ulaşarak deneyimlerini nesilden nesile aktardılar. Ancak Kepler, süreci hızlandırmak ve matematiksel hesaplamalar yoluyla aynı şeyin kısa sürede nasıl yapılacağını öğrenmek istiyordu. Meslektaşları tarafından toplanan tüm gelişmeler artık ünlü Fermat ve Newton-Leibniz teoremlerine dönüştü.

Maksimum alan sorunu

Uzunluğu 50 cm olan bir telimiz olduğunu hayal edelim, bundan en büyük alana sahip bir dikdörtgeni nasıl yapabiliriz?

Bir karara başlarken herkesin bildiği basit gerçeklerden yola çıkmalısınız. Figürümüzün çevresinin 50 cm olacağı açıktır, her iki tarafın iki katı uzunluğundan oluşmaktadır. Yani bunlardan biri “X” olarak belirlendiğinde diğerinin (25 - X) şeklinde ifade edilebileceği anlamına gelir.

Buradan X(25 - X)'e eşit bir alan elde ederiz. Bu ifade birden fazla değer alan bir fonksiyon gibi düşünülebilir. Sorunu çözmek, bunların maksimumunu bulmayı gerektirir, bu da uç noktaları bulmanız gerektiği anlamına gelir.

Bunu yapmak için birinci türevi bulup sıfıra eşitliyoruz. Sonuç basit bir denklemdir: 25 - 2X = 0.

Buradan kenarlardan birinin X = 12,5 olduğunu öğreniyoruz.

Dolayısıyla diğeri: 25 - 12,5 = 12,5.

Sorunun çözümünün bir kenarı 12,5 cm olan bir kare olacağı ortaya çıktı.

Maksimum hız nasıl bulunur?

Başka bir örneğe bakalım. Bir cisim olduğunu hayal edelim. doğrusal hareket bu, S = - t 3 + 9t 2 - 24t - 8 denklemiyle tanımlanır; burada kat edilen mesafe metre cinsinden ve süre saniye cinsinden ifade edilir. Maksimum hızı bulmamız gerekiyor. Nasıl yapılır? İndirdiğimizde hızı yani birinci türevi buluyoruz.

Denklemi elde ederiz: V = - 3t 2 + 18t - 24. Şimdi sorunu çözmek için yine ekstrem noktaları bulmamız gerekiyor. Bu, önceki görevde olduğu gibi yapılmalıdır. Hızın birinci türevini bulup sıfıra eşitliyoruz.

Şunu elde ederiz: - 6t + 18 = 0. Dolayısıyla t = 3 s. Bu, vücudun hızının kritik bir değere ulaştığı zamandır. Ortaya çıkan verileri hız denkleminde yerine koyarız ve şunu elde ederiz: V = 3 m/s.

Ama ne olduğunu nasıl anlıyorsunuz? azami hızÇünkü bir fonksiyonun kritik noktaları onun en büyük veya en küçük değerleri olabilir mi? Kontrol etmek için hızın ikinci türevini bulmanız gerekir. Eksi işaretiyle 6 sayısıyla ifade edilir. Bu, bulunan noktanın maksimum olduğu anlamına gelir. Ve durumda pozitif değer ikinci türev minimum olacaktır. Bu, bulunan çözümün doğru olduğu anlamına gelir.

Örnek olarak verilen problemler, bir fonksiyonun ekstremum noktalarını nasıl bulacağınızı bildiğiniz takdirde çözülebilecek problemlerin sadece bir kısmıdır. Aslında bunlardan çok daha fazlası var. Ve böyle bir bilgi, insan uygarlığı için sınırsız olanaklara kapı açar.

İşlev y = f(x) denir artan (azalan) belirli bir aralıkta, eğer x 1 için< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).

Türevlenebilir fonksiyon y = f(x) bir aralıkta artarsa ​​(azalırsa), o zaman bu aralıktaki türevi f " (X)> 0

(F"(X)< 0).

Nokta X Ö isminde yerel maksimum nokta (minimum) fonksiyon f(x) eğer noktanın bir komşuluğu varsa x-o f(x) eşitsizliğinin doğru olduğu tüm noktalar için≤ f (xö) (f(x)≥ f(x0)).

Maksimum ve minimum noktalara denir ekstrem noktalar ve fonksiyonun bu noktalardaki değerleri onun aşırılıklar.

Ekstrem noktalar

Gerekli koşullar ekstremum . Eğer nokta X Ö f(x) fonksiyonunun uç noktasıdır, o zaman ya f " (x o ) = 0 veya f(xo) mevcut değil. Bu tür noktalara denir kritik, ve fonksiyonun kendisi kritik noktada tanımlanır. Bir fonksiyonun ekstremum değerleri kritik noktaları arasında aranmalıdır.

İlk yeterli koşul. İzin vermek X Ö - kritik nokta. Eğer f" (x ) bir noktadan geçerken X Ö artı işaretini eksi olarak değiştirir, ardından bu noktada x-o fonksiyonun bir maksimumu vardır, aksi takdirde bir minimumu vardır. Kritik noktadan geçerken türev işaret değiştirmiyorsa, o noktada X Ö aşırı bir durum yok.

İkinci yeterli koşul. f(x) fonksiyonu şuna sahip olsun:
F" (x ) noktanın yakınında X Ö ve kendi noktasındaki ikinci türev f "" (x 0) x-o. Eğer f"(x-o) = 0, f "" (x 0)>0 (f "" (x 0)<0), то точка x-o f(x) fonksiyonunun yerel minimum (maksimum) noktasıdır. Eğer f "" (x 0) = 0 ise, o zaman ya ilk yeterli koşulu kullanmanız ya da daha yüksek olanları dahil etmeniz gerekir.

Bir parça üzerinde y = f(x) fonksiyonu minimum veya maksimum değerine kritik noktalarda veya parçanın uçlarında ulaşabilir.

Örnek 3.22.

Çözüm.Çünkü F " (

Bir fonksiyonun ekstremumunu bulma problemleri

Örnek 3.23. A

Çözüm. X Ve sen sen
0 ≤ X≤
> 0 ve ne zaman x >a /4S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение işlevler kv. birimler).

Örnek 3.24. p ≈

Çözüm. p p
S"
R = 2, H = 16/4 = 4.

Örnek 3.22.f (x) = 2x 3 - 15x 2 + 36x - 14 fonksiyonunun ekstremumunu bulun.

Çözüm.Çünkü F " (x ) = 6x 2 - 30x +36 = 6(x ​​-2)(x - 3), o zaman fonksiyonun kritik noktaları x 1 = 2 ve x 2 = 3 olur. Ekstremum ancak bu noktalarda olabilir. x 1 = 2 noktasından geçerken türevin işareti artıdan eksiye değiştiği için, bu noktada fonksiyonun bir maksimumu vardır. x 2 = 3 noktasından geçerken türevin işareti eksiden artıya değişir, dolayısıyla x 2 = 3 noktasında fonksiyonun minimumu vardır. Fonksiyon değerlerini noktalarda hesapladıktan sonra
x 1 = 2 ve x 2 = 3, fonksiyonun ekstremumunu buluyoruz: maksimum f (2) = 14 ve minimum f (3) = 13.

Örnek 3.23.Taş duvarın yanına, üç tarafı tel örgüyle çevrilecek, dördüncü tarafı duvara bitişik olacak şekilde dikdörtgen bir alan inşa etmek gerekiyor. Bunun için var A doğrusal metre örgü. Site hangi en boy oranında en geniş alana sahip olacak?

Çözüm.Platformun kenarlarını şu şekilde belirtelim: X Ve sen. Sitenin alanı S = xy'dir. İzin vermek sen- bu, duvara bitişik tarafın uzunluğudur. O halde koşula göre 2x + y = a eşitliği sağlanmalıdır. Dolayısıyla y = a - 2x ve S = x (a - 2x), burada
0 ≤ X≤ a /2 (alanın uzunluğu ve genişliği negatif olamaz). S " = a - 4x, a - 4x = 0, x = a/4'te, dolayısıyla
y = a - 2 × a/4 =a/2. Çünkü x = a/4 tek kritik noktadır, bu noktadan geçerken türevin işaretinin değişip değişmediğini kontrol edelim. x a /4 S'de "> 0 ve ne zaman x >a /4S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение işlevler S(a/4) = a/4(a - a/2) = a 2 /8 (kv. birimler). S sürekli olduğundan ve S(0) ile S(a/2) uçlarındaki değerleri sıfıra eşit olduğundan bulunan değer, fonksiyonun en büyük değeri olacaktır. Dolayısıyla problemin verilen koşulları altında sitenin en uygun en boy oranı y = 2x'tir.

Örnek 3.24.Kapasitesi V=16 olan kapalı silindirik tank imalatı gerekmektedir. p ≈ 50 m3. Üretiminde en az miktarda malzemenin kullanılması için tankın boyutları (yarıçap R ve yükseklik H) ne olmalıdır?

Çözüm.Silindirin toplam yüzey alanı S = 2'dir P R(R+H). Silindirin hacmini biliyoruz V = p R 2 Н Þ Н = V/ p R 2 =16 p / p R2 = 16/R2. Yani S(R) = 2 P (R2+16/R). Bu fonksiyonun türevini buluyoruz:
S"(R) = 2 p (2R-16/R2) = 4 p (R-8/R2). S" R3 = 8'de (R) = 0, dolayısıyla,
R = 2, H = 16/4 = 4.